Research ArticleClinical Practice of Molecular Radiotherapy

Dosimetry of Internal Emitters

George Sgouros
Journal of Nuclear Medicine January 2005, 46 (1 suppl) 18S-27S;

Abstract

Response and toxicity prediction is essential to rational implementation of cancer therapy. The biologic effects of radionuclide therapy are mediated via a well-defined physical quantity, the absorbed dose, which is defined as the energy absorbed per unit mass of tissue. The concepts, basic definitions, and different approaches to the clinical implementation of absorbed dose estimation are reviewed in this article. Ongoing efforts to improve the accuracy of dosimetry calculations are discussed, as well as studies examining the relationship between absorbed dose and response. Particular attention is placed on the marrow and kidney as dose-limiting organs. Finally, the potential role of radiobiologic modeling in helping to account for differences in dose rate and spatial distribution are reviewed. A treatment planning approach to radionuclide therapy will eventually require incorporation of biologic and radiobiologic considerations. Until such methods are developed and validated, absorbed dose remains an important variable—but still one of several— likely to predict response in an individual patient.

Response and toxicity prediction is essential to the rational implementation of cancer therapy. Unlike most other systemic treatments, the biologic effects of radionuclide therapy are mediated via a well-defined physical quantity, the absorbed dose, which is defined as the energy absorbed per unit mass of tissue. Long- and well-established cancer treatment experience in radiotherapy has provided ample evidence that absorbed dose may be used to predict biologic response (1).

To state that absorbed dose alone would predict response is an oversimplification, however. As has been recognized in radiotherapy and is beginning to be appreciated in radionuclide therapy, the rate at which the absorbed dose is delivered, the manner by which it is delivered (β-particles, α-particles, or Auger electrons), the radiobiologic characteristics of the tumor or normal organ, and the treatment history of the patient all affect response to a specific total absorbed dose (2).

The concepts, basic definitions, and different approaches to the clinical implementation of absorbed dose estimation are reviewed in this article. Current efforts to improve absorbed dose estimates by using more realistic anatomic models and implementing radiobiologic models that can be used to account for dose rate and uniformity are also reviewed. Throughout this review, response is defined as an acute, deterministic response, such as toxicity or tumor shrinkage, rather than a stochastic or carcinogenic effect, such as leukemia.

ABSORBED DOSE DEFINED

It is important at the outset to make a distinction between the terms “absorbed dose” and “dose.” The term “dose” does not have a precise meaning in radionuclide dosimetry. In practice, this term has been used to describe administered activity as well as absorbed dose. In most cases, the distinction can be made on the basis of context. The appropriate term for the quantity of interest in dosimetry, however, is absorbed dose (D), expressed in units of Gray (“rad” in older texts; 1 Gy = 100 rad). This is defined as the energy (E) absorbed in a particular mass of tissue, divided by the tissue mass (M): MathEq. 1 In radionuclide therapy: MathEq. 2 Math Math

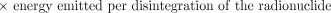
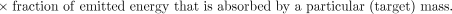
Cumulated Activity

The first term in the expression for E depends on the half-life of the radionuclide and its spatial and temporal distribution. The latter are typically obtained by imaging or sampling. In a typical clinical scenario, images collected at different times after injection of the radiopharmaceutical are used to estimate the amount or concentration of radioactivity in a specific region. The level of activity obtained at different times after injection, plotted against time, gives a time-activity curve for a particular organ. The integral of this curve gives the total number of disintegrations or the cumulated activity (Ã) for the region. This is illustrated in Figure 1. In general, the cumulated activity must be determined for each patient.

FIGURE 1.
FIGURE 1.

Sample time-activity curve for the liver (LI) is depicted. Open circles represent measured time points. Solid line is monoexponential fit to data given by expression A(t), where A0 is injected activity, λeff is effective clearance rate given by (Ln(2)/Tp + Ln(2)/Tb), and fLI is fraction of administered activity in liver, back-extrapolated to injection time. Integral of expression from t = 0 to infinity gives expression shown in box. Residence time (τ) may be derived as shown in second box.

Energy Emitted Per Disintegration

The next term in equation 2 is the total energy emitted per disintegration (Δ) of the radionuclide. This is a property of the radionuclide and is independent of all other factors involved in estimating absorbed dose. It may be obtained from standard physics or dosimetry tables (3,4). The total energy emitted is usually tabulated according to emission type (e.g., photon, β-particle, Auger electron, or α-particle).

Absorbed Fraction

The last term in equation 2 accounts for the emission type, energy, and also the geometry and characteristics of the source and target tissue to provide a net factor that converts the total energy emitted in a particular source region to that absorbed in the region (i.e., self-dose) or in other regions (i.e., cross-organ dose). This absorbed fraction factor (φ) is generally determined by Monte Carlo calculation (5,6).

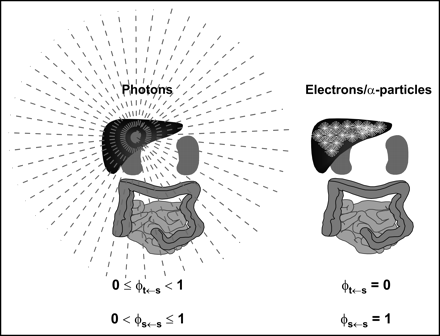
The spectrum of emission types will determine the fraction of energy emitted by a radionuclide that is absorbed by a particular target mass. Radionuclide emissions may be broadly categorized according to their absorption properties. Particulate emissions, such as β- or α-particles are generally absorbed within the tissue of origin. Photons, depending on their energy, will deposit energy in both the source tissue and other adjacent and nonadjacent tissues (Fig. 2).

FIGURE 2.
FIGURE 2.

Different tissue absorption properties of photons versus electron or α-particle emissions of radionuclide are illustrated. Photons originating in liver, for example, depending on energy, can irradiate distant organs. Correspondingly, not all of photon energy emitted within source organ will be absorbed by source organ, as reflected in possible range of absorbed fraction values for photons. In contrast, great majority of electron (Auger and β-particles) or α-particle energy will be absorbed very close to emission source and within source tissue. Correspondingly, energy absorption to other tissues is negligible.

MIRD COMMITTEE SCHEMA

Once the numerator of equation 1 has been obtained (i.e., the energy absorbed in a target mass), it is divided by the mass of the target to yield the absorbed dose to the target. Symbolically, the equation is expressed as follows: MathEq. 3 where ÃS = cumulated activity in source region S; Δ = energy emitted by the radionuclide per disintegration; φT←S = fraction of energy emitted by the radionuclide in source region S that is absorbed in the target region, T; and MT = mass of region T.

This general equation is the starting point for most current approaches to absorbed dose estimation. The equation describes the dose contribution to a target region from a single region.

The derivation as well as the conceptual framework used to arrive at this expression is attributed to the early work of the MIRD Committee, which also established the most commonly used practical approach for estimating absorbed dose. This was accomplished by isolating and tabulating values for those factors of the absorbed dose calculation that can be generalized. As illustrated in Figure 3, the MIRD Committee reduced equation 3 into a product of 2 values, the cumulated activity in a source region and S, the absorbed dose to a target region per unit cumulated activity in the sources (7). The total absorbed dose (DT) to a target region (T) is then the sum of dose contributions to the target from different source regions: MathEq. 4

FIGURE 3.
FIGURE 3.

MIRD schema is illustrated. Terms in absorbed dose equation that are independent of radionuclide biodistribution have been compiled and tabulated as S values. S values are tabulated for individual radionuclides according to source-target region pairs. When source-target regions are individual organs or subregions of organs, fixed geometry models are required to establish geometry, relative orientation, composition, and mass of different source-target organs or organ subregions.

The absorbed fractions (φT←S) required to obtain S values were calculated by generating an idealized model of human anatomy defined as a collection of appropriately placed distinct organ volumes with mass and composition that were selected to reflect a typical or standard human anatomy (i.e., standard man), later extended to include female and pediatric models (8). For each radionuclide, a certain number of decays were uniformly distributed throughout each idealized organ volume, and the absorbed fraction from each source-target organ pair was calculated by Monte Carlo simulation. The original calculations were performed in the late 1970s, and, given the limited computational power available at the time, several simplifying assumptions were made to perform these calculations (6). Application of the resulting S values, therefore, to patient anatomies that deviate substantially from the idealized model will lead to errors. Furthermore, use of a standard model precluded the tabulation of S values for tumors, because tumors do not come in standard dimensions or positions. In diagnostic nuclear medicine, this has not been a concern, because the absorbed doses to normal organs are of interest and also because the administered activities generally used are well below levels that can result in toxicity. In therapeutic nuclear medicine, however, the absorbed dose to tumors is important in evaluating treatment efficacy. Accurate estimation of the absorbed dose to normal organs is also important in assessing likely toxicity. The dosimetry requirements of therapeutic nuclear medicine have led to ongoing interest and improvements in radionuclide dosimetry (9). Notable advances are briefly summarized in the following sections.

Extensions to Idealized Phantom Geometries

Since publication of the initial S value table by the MIRD Committee, additional S values have been generated to facilitate absorbed dose estimation for anatomies and dose distributions that differ from the original anthropomorphic phantom. In addition to female and pediatric S value tables, S values have also been generated for organ subregions and for cellular dimensions (10–16,17). The latter make it possible to estimate the mean absorbed dose to the nuclear or whole cell volume from a uniform distribution of activity in different cellular compartments (e.g., cell surface, cytoplasm). These extensions reflect the generality of the MIRD Committee formalism. To support the calculation of nonuniform absorbed doses and to account for nonuniform activity distributions at the level of imaging instrumentation voxels, the MIRD Committee has also published S value tabulations for different voxel sizes and source-target voxel distances (18). The resulting S value tabulations facilitate absorbed dose calculations by separating potentially lengthy and complex Monte Carlo calculations from the task of estimating absorbed dose. Because use of previously tabulated S values requires a fixed anatomic model, this approach is not easily amenable to geometries that deviate substantially from the fixed anatomic models. Voxel S values overcome this problem and have been adopted in several dose calculation programs (19–21).

Fixed Geometry-Based Dosimetry Software

Several software packages have been developed to implement the S value methodology. The most widely-used of these, MIRDOSE3, incorporates S factors for 223 radionuclides and 10 different anthropomorphic models, including standard male, female, and pediatric geometries (22). This software is no longer being distributed and has been replaced by Organ Level Internal Dose Assessment (OLINDA; Vanderbilt University). OLINDA is U.S. Food and Drug Administration (FDA) approved as a device and includes S values specific to 10 phantoms and 5 organ models for more than 800 radionuclides, including α-particle emitters, which were not previously included in S value tabulations. The program also includes a pharmacokinetic module that may be used to determine organ cumulated activities.

MABDOSE (University of Colorado), another package that also implements fixed geometry, allows the user to place spherically shaped tumors within the simplified anatomic model originally described by the MIRD Committee. To do this, an on-the-fly Monte Carlo simulation was incorporated into the code (23,24). This method could accommodate tumor dosimetry within the idealized geometry defined by the MIRD Committee.

Tumor Dosimetry

As noted previously, fixed anatomic models are not easily amenable to tumor dosimetry. Several approaches have been developed for estimating absorbed dose to tumors and the dose contribution from tumors to normal organs. The simplest approximation is made by assuming that all electrons are deposited locally and that the relative contribution to the tumor absorbed dose from photons is negligible. Alternatively, the fraction of electron energy absorbed may be considered, assuming the tumor can be modeled as a sphere (4,5). This is an important correction for tumors with diameters in the range of the path length of electron emissions. Depending on the radionuclide, this correction should be made for tumors with diameters <0.5–1 cm. The photon contribution to larger tumors becomes relevant as tumor diameter increases. Using tables of photon absorbed fraction to spheres or ellipsoids, the photon self-dose may be added by assuming that the tumor is a sphere or ellipsoid (6). If this assumption is made, the photon dose to and from normal organs may also be calculated by placing the idealized tumor geometry in a defined position relative to the standard geometry used for the S factor calculations. If a point-kernel convolution technique is used in estimating absorbed dose, the true tumor and normal tissue geometry as well as the activity distribution may be considered to yield a spatial absorbed dose or dose-rate distribution (20,21,25–31). Tissue composition and density variations are not easily accounted for using point-kernel techniques. To account for these, Monte Carlo techniques are needed to estimate absorbed dose (32–39).

THREE-DIMENSIONAL (3D) IMAGING-BASED DOSIMETRY

The increase in computer processing power and the availability of 3D imaging methodologies, particularly with SPECT/CT and PET/CT, have provided an impetus for direct image-based dosimetry techniques. The essential requirements for 3D imaging-based dosimetry are (a) the availability of 3D anatomic imaging studies such as CT or MRI; (b) at least 1 3D imaging study of the radioactivity distribution (e.g., PET or SPECT); and (c) software that implements a point-kernel or Monte Carlo calculation methodology to estimate the spatial distribution of absorbed dose. To define the anatomy and also provide tissue density information, a CT scan over the region of interest is required. To provide the activity distribution, a PET or SPECT scan is required. If absorbed dose rather than absorbed dose rate is desired, then kinetic information is required. In conventional dosimetry, kinetic information that is averaged over the whole source organ volume suffices. In 3D dosimetry, however, variations in pharmacokinetics within an organ must be considered. Ideally, kinetic information on a voxel-by-voxel basis should be used. This would require multiple SPECT or PET studies taken over time, each registered to the other as well as to the CT study. Assuming such data are available, a voxel-by-voxel-based integration of the activity would have to be performed to yield a 3D representation of residence time or cumulated activity. Alternatively, it is possible to derive a residence time or cumulated activity image by using planar imaging to obtain kinetics and SPECT or PET to obtain spatial distribution. This is a compromise and represents an approximation to the actual cumulated activity, because different organs (or tissues) with different kinetics may be superimposed on planar views. The residence time or cumulated activity image may be obtained by assuming that all points making up the spatial distribution of activity follow the same kinetics. The mean dose over a target volume is determined by taking the mean of all values in the dose array. Either integral or differential dose-volume histograms can be generated. In the former, the percentage of volume receiving less than or equal to a particular dose value is plotted as a function of the dose value. In the latter, the percentage of volume receiving a particular absorbed dose range is plotted versus the dose range. The dose distribution can also be displayed as an image or as isodose levels superimposed on anatomic or radioactivity images.

3D Imaging-Based Dosimetry Software

Many researchers have pursued and contributed to 3D imaging-based patient-specific dosimetry (21,23,29–31,33–36,39). This section will focus on the 2 most fully developed packages, 3D Internal Dosimetry (3D-ID) and DOSIMG (Lund University, Lund, Sweden) (33,40).

The 3D-ID software package takes the distribution of radiolabeled antibody for a given patient (from SPECT or PET) and combines it with anatomic information (from CT or MRI) to yield absorbed dose estimates that are specific to a particular patient’s biodistribution and anatomy (25,30,41–43). This work introduced the concept of dose-volume histograms for internally administered radionuclides (44). The 3D-ID software package may be used to perform both Monte Carlo and point-kernel-based calculations. It has been used to examine the impact of different radionuclides on dose distribution, given a fixed cumulated activity distribution (34). 3D-ID has been used to perform a detailed analysis of tumor dose versus response in the treatment of non-Hodgkin’s lymphoma (NHL) using 131I-anti-B1 antibody (42). The point-kernel module in 3D-ID and data from a clinical trial of 131I-labeled anti-B1 antibody were used. The analysis did not reveal a statistically significant dose-response relationship. Using a more robust and validated SPECT quantitation methodology in patients who had not been treated previously, Koral et al. (45) were able to demonstrate a dose-response relationship. This was observed only in a selected subset of 15 (pelvic or abdominal) tumors (identified on CT and <10 cm3 in size) out of 43 in a subset of an already selected patient population (partial responders). More recently, 3D-ID has been used in thyroid cancer patients with 124I PET data and CT (43). This study demonstrated the use of multiple PET image studies registered across time and integrated, voxel by voxel, to provide a 3D cumulated activity image used in the dosimetry calculation.

The DOSIMG software has been used with mathematical anthropomorphic phantoms to examine the impact of different quantitative SPECT algorithms on Monte Carlo-derived absorbed dose calculations. Mathematical phantom-derived CT and SPECT images were generated, and dose calculations derived from these were compared with “true” dose results derived from the actual mathematical phantom data (46). The SPECT quantitation methodologies derived from this work were subsequently applied to 111In/90Y dosimetry (47).

RED MARROW DOSIMETRY

In the majority of nonmyeloablative radionuclide therapy, red marrow toxicity is dose limiting. As a result, the red marrow has received the greatest attention in terms of developing and examining dosimetry methodologies (48–55). The dosimetry approaches may be broadly categorized as blood based or imaging based, depending on whether or not the radiopharmaceutical specifically localizes to blood, bone, or marrow components, including tumor micrometastases in the marrow. A comprehensive review and recommendations for performing marrow dosimetry have been published in the case that the radiopharmaceutical binds to blood, bone, or marrow components (51). If this does not occur, then blood-based methods that relate the activity concentration of the radiopharmaceutical in blood or plasma to the concentration in the red marrow have been described (48,49). It is important to note that these methods are largely specific to intact radiolabeled antibodies. In particular, by assuming rapid equilibration of radiolabeled antibodies in the plasma and extracellular fluid of the red marrow, a factor of 0.3–0.4 may be derived that relates the concentration of radioactivity in the red marrow to that in the blood (the red marrow-to-blood ratio). In murine studies, this range of concentration ratios has been confirmed experimentally for intact, 150-kD antibodies but not for lower molecular weight fragments that yield a red marrow-to-blood concentration ratio closer to 1 (53).

DOSE-RESPONSE RELATIONSHIPS

The raison d’être for internal emitter dosimetry is to predict response and toxicity. In part, because radionuclide therapy (with the exception of radioiodine treatment for thyroid disease) is a relatively new field, few human studies have been reported that specifically address this question. As a result, the dose-response experience of external beam radiotherapy is used to evaluate potential tumor response or normal organ toxicity. The few reports specifically examining dose-response relationships in humans are briefly reviewed.

Tumor

Because radioimmunotherapy of NHL has resulted in measurable responses, several studies have examined tumor response versus absorbed dose in NHL. In addition to the 2 anti-CD20 antibody reports cited previously, the dose-response relationship in NHL for an anti-CD22 antibody labeled with 90Y has been examined, and no relationship between tumor response (assessed as the percentage change in the sum of perpendicular diameters) and absorbed dose (determined by planar imaging of 111In and using MIRDOSE3) was observed (42,45,56). The authors concluded that this can be partly attributed to the biologic activity of the unlabeled antibody as well as other biologic factors affecting treatment response, as suggested by recent findings of genetic correlates with treatment response to rituximab (57). It is important to note that different dosimetry methodologies were used for these 3 NHL dose-response studies, and the methodology used to estimate absorbed doses will affect dose-response correlations. In solid tumor targeting, a recent review of reported biodistribution, dosimetry, and outcome in radiolabeled CC49 antibody trials found that the reported tumor absorbed-dose estimates were more variable than normal organ absorbed-dose estimates and also found a wide variability in reported dosimetric parameters and methodologies (58). The observation was made that standardization and improved dosimetry may aid in establishing dose-response relationships. In addition to the dosimetry calculation methodology, standardization of data acquisition is also important. A MIRD pamphlet is available that outlines a standard approach to data acquisition (59).

In radiopeptide therapy, wherein substantially higher tumor absorbed doses may be delivered (because marrow toxicity is less limiting as a result of rapid clearance of the radiopeptide from the circulation), a robust tumor dose-response relationship has been observed (60).

Red Marrow

The red marrow is a complex, distributed organ and presents challenges both in terms of estimating activity concentration kinetics for cumulated activity determination and also for Monte Carlo calculation of absorbed fractions.

In estimating the cumulated activity, progress has been made toward adopting a standardized, blood-based approach, and several red marrow dose-response studies have been reported (61–67). One such study found that absorbed dose to the red marrow or total body predicted hematologic toxicity better than administered activity or administered activity per meter squared (67). The analysis and conclusions were confined to 131I-labeled antibodies and antibody fragments that did not bind to blood, bone, or marrow cellular components. Consistent with this observation and based on toxicity correlations in phase I/II trials, the 131I-labeled anti-CD20 antibody, tositumomab (Bexxar; GlaxoSmithKline), which was recently approved by the FDA for treatment of NHL, is prescribed to patients according to total body absorbed dose (68,69). Absorbed dose versus toxicity studies for another FDA-approved anti-CD20 antibody labeled with 90Y, ibritumomab tiuxetan (Zevalin; Biogen Idec), did not show a correlation of absorbed dose with toxicity. As a result, this agent is prescribed on a per-body-weight basis (70,71). The different dose-response observations and prescription schemes have been explained primarily by the difference in half-lives and retention properties of the 2 radionuclides, 131I and 90Y. 131I-labeled antibody is subject to dehalogenation and urinary excretion as free 131I. Given, the 8-d half-life of 131I, interpatient variation in dehalogenation and urinary excretion will substantially affect the whole body and marrow absorbed dose. In contrast, the shorter 2.7-d half-life of 90Y, combined with its chelate conjugation to antibodies, is subject to reduced urinary excretion as free 90Y. In addition to the reduced excretion rate of 90Y-labeled anti-CD20 antibody, the requirement that 90Y kinetics be derived from 111In imaging could also provide a plausible explanation for the absence of a dose-response relationship in this case. The surrogate, 111In, is used for 90Y because 90Y does not emit photons that are easily imaged. It is a pure β-emitter and only bremsstrahlung photons are emitted. In this case, prior treatment and bone marrow reserve have been shown to be better predictors of marrow toxicity. Because patients undergoing radioimmunotherapy have been previously exposed to chemotherapy, the impact of such prior therapy on bone marrow reserve is important in evaluating and interpreting hematopoietic dose-response studies. In this regard, plasma levels of FLT3-L, a cytokine involved in regulating hematopoietic recovery by stimulating hematopoietic proliferation after chemotherapy, has been found useful as a predictor of marrow radiosensitivity that can be used to adjust the anticipated biologic effect of a specific red marrow absorbed dose (72).

All red marrow dosimetry performed to date has relied on a highly stylized representation of the marrow. More detailed representations have recently been developed and are being used to perform Monte Carlo calculations for generating more accurate S values (73–83).

Kidney

Recent instances of irreversible renal toxicity have highlighted the kidney as a possible dose-limiting organ (84–89). The concern over renal toxicity reflects several developments in therapeutic nuclear medicine. Although the developments are highly diverse (encompassing, for example, peptide-mediated receptor targeting, metabolic targeting using bone-seeking radionuclides, and engineered low-molecular-weight multivalent targeting), these can all be generally described as a shift to constructs that have molecular weight substantially lower than the 150,000 Da of intact antibodies (86,88,90). These generally clear from the circulation very rapidly (T1/2 < 1–5 h) and are excreted through the kidneys. Because clearance is so rapid, the red marrow is generally not the dose-limiting organ (assuming no specific uptake in the marrow); instead, renal toxicity becomes a concern. This is best illustrated in the case of peptides that target the somatostatin receptor found on neuroendocrine tumors. The rapid clearance and observed large variations in tumor uptake have required administration of very large levels of radioactivity to deliver effective tumor doses. Clearance through and prolonged retention in the kidneys have resulted in very high kidney absorbed doses that approach or, in fractionated treatment protocols, have exceeded the radiotherapy-derived 23-Gy tolerance limits (which yield nephropathy in 5% of the exposed population in 5 y) (91). As might be expected, the incidence of renal pathology has been highly dependent on the radionuclide used. The Auger-emitter 111In, with particle ranges that are less than a cell diameter, has shown minimal toxicity at estimated kidney absorbed doses of 45 Gy (cumulative administered activities of 58 GBq/m2), whereas 90Y, with long-range emissions of 5 mm in tissue (90% of β-energy deposited in a 5-mm radius sphere), has led to renal toxicity at administered activities in the 1.9 GBq/m2 range (84,92).

Renal toxicity has also been observed in a bone marrow ablation trial using 166Ho-1,4,7,10-tetraazacyclododecane-1,4,7,10-tetramethylene-phosphonic acid in patients with multiple myeloma (88,93). Rapid clearance via the kidneys with minimal kidney retention was observed. The range of estimated kidney absorbed doses was 2.6–14 Gy, well below the 23-Gy tolerance limit (91). Despite this, renal dysfunction was observed in 36% of patients treated, and grade 3 or higher toxicity was observed in 17% of the treated population. Although the treatment protocol included chemotherapy and external radiotherapy, a statistical analysis showed that injected activity per body weight was the only factor with a significant effect on renal toxicity. Radiobiologic analysis of these data has suggested that the very high dose rate resulting from transit of 17–170 GBq 166Ho through the kidneys resulted in absorbed dose rates that translated to biologically effective doses of 40–50 Gy, depending on the radiobiologic parameters used (94,95). These experiences have placed a greater emphasis on improving kidney dosimetry and better understanding of the radiobiologic implications of absorbed dose nonuniformity and delivery rate (15,94–99).

FUTURE DIRECTIONS

As nuclear medicine has grown to include a substantial therapeutic component, the importance of radionuclide dosimetry has also grown. The expectation that radionuclide dosimetry could be used to plan radionuclide therapy in the same way that dosimetry is used to plan external beam radiotherapy has yet to be met. In large part, this unfulfilled expectation is the direct result of the many variables involved in determining the biologic effect of targeted radionuclides. In many but certainly not all instances the most important variables are biologic rather than dosimetric, making radionuclide dosimetry an important—but not the only—determinant of response. To achieve the treatment planning objective in radionuclide therapy, it is important to understand and distinguish between response results dominated by biologic factors versus dosimetry. It is essential, therefore, that ongoing improvements in dosimetry methodology continue so that the role of dosimetry relative to biologic factors is properly evaluated.

Table 1 lists the dosimetric parameters relevant to tumor or normal organ response. Current routinely available dosimetry software provides the first item on the list as a mean absorbed dose averaged over an idealized, spherical tumor or fixed normal organ volume. As indicated previously, efforts to improve on this by providing the spatial distribution of absorbed dose to individual patient anatomy are gaining prominence, and many groups are developing software to accomplish this. An important challenge in these efforts is to provide output that helps in the interpretation of the results. Accurate, detailed absorbed dose calculations are useful only to the extent that they are biologically relevant and easily interpretable.

View this table:
TABLE 1

Dosimetric and Radiobiologic Parameters in Predicting Tumor Response or Normal Organ Toxicity

The uniformity (or lack thereof) of absorbed dose distributions and their biologic implications have been examined intensively, primarily in animal studies (100–108). To address the question of how to best represent the large amount of data in 3D distributions of absorbed dose, it is useful to borrow from the radiotherapy field. One possible approach would be dose-volume histograms to represent dose distributions in targeted radionuclide therapy (44). Another approach is the equivalent uniform dose (EUD) model (104). The EUD model takes this a step farther by introducing the radiobiologic parameters, α and β (the sensitivity per unit dose and per unit dose squared, respectively, in the linear-quadratic dose-response model), to convert the spatially varying absorbed dose distribution into an equivalent uniform absorbed dose value that would yield a biologic response similar to that expected from the original dose distribution.

To date, the rate of absorbed dose delivery has been largely ignored. In addition to the extensive evidence in external radiotherapy, there is also some evidence in radionuclide therapy that absorbed dose rate should not be neglected in trying to predict response. Such preliminary evidence has been cited here for renal toxicity and has also been reported regarding bone marrow toxicity (53). The importance of dose rate will increase as lower molecular weight agents that clear rapidly and that require greater administered activities gain widespread use. In an analogy to the EUD model for evaluating and comparing different spatial distributions of absorbed dose, the biologically effective dose (BED) model may be used to compare the response implications of total absorbed doses delivered at different dose rates. Detailed derivations and reviews of this model and examples of its application to radionuclide therapy have been published (95,109–111). In essence, the approach is similar to that of EUD, in that a particular dose-rate profile is converted to a reference dose rate, based on a radiobiologic model that translates dose-rate distribution to expected response.

Although potentially useful in representing complex spatial and temporal distributions of absorbed dose, such simplification must be implemented with caution, because they rely on the biologic models used and on the model parameters chosen for the calculation. Calculation of EUD requires knowledge of the linear-quadratic model parameters α and β. In addition to these, the BED calculation requires knowledge of μ, the repair rate (assuming exponential repair) for radiation-induced DNA damage. It is important to note that these parameters will be influenced by prior therapy.

The 3 parameters, α, β, and μ, are related to radiosensitivity and, as indicated in Table 1, will be spatially dependent as they are related to hypoxia and proliferation rate. Since these parameters are also highly relevant to response in external radiotherapy, imaging-based measurements are already being investigated (112). As noted, radiosensitivity will also be modulated by exposure to prior therapeutics.

The last item listed in Table 1 relates to the observation that normal organs are hierarchical and that the consequences of radiation damage are highly dependent on the particular group or class of cells that are irradiated and that may arise either by cross-fire from adjacent cells or activity-containing vasculature or by directly concentrating the radiolabeled agent or radionuclide. The “criticality” parameter, therefore, is intended to reflect the likelihood that damage to a particular group of cells will lead to organ failure. Such a parameter is particularly relevant to the kidney, wherein radiation-induced renal failure is generally associated with damage to endothelial cells of the glomerular capillaries (thrombotic microangiopathy) (84,97).

SUMMARY

The biologic effects of radionuclide therapy are mediated via a well-defined physical quantity, the absorbed dose, which is defined as the energy absorbed per unit mass of tissue. This basic formulation, as well as subsequent practical methodologies for estimating absorbed dose, were established by the MIRD Committee, which first published a table of S values, making it possible to convert cumulated activity in different organs to absorbed dose. A fixed geometry model was adopted to calculate S values. S values derived from fixed geometry models have the advantage of not requiring point-kernel or Monte Carlo calculations in estimating absorbed dose. The requirements of therapeutic nuclear medicine have led to ongoing refinements in the fixed geometry models used to derive S values, such that several organ-specific and whole-body age-specific models have been developed and are included in OLINDA, an FDA-approved software package that implements the fixed model approach to absorbed dose calculation. Fixed geometry models have the disadvantage, however, of not matching the actual patient anatomy. This disadvantage is being addressed by developments in 3D imaging-based patient-specific dosimetry software. Examination of whether such new dosimetry methodologies lead to improved dose-response relationships has only recently begun. Such studies are highly dependent on the availability of response data from radionuclide therapy trials. More such data are needed if ongoing improvements in dosimetry methodologies are to be validated against the clinically relevant measure of response prediction. Comparison of dose-response studies from different institutions will require a standardized absorbed dose methodology. Such standardization has been generally achieved for red marrow dosimetry but remains an important problem for normal organ or tumor dosimetry. Recent evidence of renal toxicity at total absorbed doses thought to be safe based on experience in radiotherapy has highlighted the need to examine additional dosimetric parameters such as dose rate and spatial distribution. The translation of such additional data into response probability will require radiobiologic modeling. Such modeling depends critically on the availability of the relevant parameters and on an understanding of how these change after chemotherapy or external beam radiotherapy.

CONCLUSION

In conclusion radionuclide dosimetry is still at an early stage of development. Active research toward developing patient-specific 3D imaging-based dosimetry, coupled with the availability of faster computers, improved Monte Carlo methods, and dual anatomy/radioactivity imaging devices, will improve the physics of absorbed dose estimation. Because these techniques will affect clinical trial expense and patient comfort, the gain from such improvements must be rigorously tested in terms of improved response prediction. A treatment planning approach to radionuclide therapy will eventually require incorporation of biologic and radiobiologic considerations. Efforts in this direction are just beginning. Until such methods are developed and validated, however, absorbed dose remains an important variable—but still one of several—likely to predict response in an individual patient.

Acknowledgments

Support from the National Institutes of Health (grants R01 CA62444, R01 CA 72683, and P01 CA33049) and from the U.S. Department of Energy (grant DEFG02-86ER-60407) are gratefully acknowledged.

Footnotes

  • Received Aug. 9, 2004; revision accepted Nov. 17, 2004.

    For correspondence or reprints contact: George Sgouros, PhD, Department of Radiology, Johns Hopkins University, School of Medicine, 720 Rutland Ave, Baltimore, MD 21205.

    E-mail: gsgouros{at}jhmi.edu

REFERENCES

  1. ↵
    Hellman S. Principles of cancer management: radiation therapy. In: Devita VT, Hellman S, Rosenberg SA, eds. Cancer: Principles and Practice of Oncology. Philadelphia, PA: Lippincott Williams & Wilkins; 2001:265–288.
  2. ↵
    Hall EJ. Radiobiology for the Radiologist. Philadelphia, PA: JB Lippincott Co.; 1994.
  3. ↵
    Browne E, Firestone RB. Table of Radioactive Isotopes. New York, NY: John Wiley & Sons; 1986.
  4. ↵
    Weber DA, Eckerman KF, Dillman LT, Ryman JC. MIRD: Radionuclide Data and Decay Schemes. New York, NY: Society of Nuclear Medicine; 1989.
  5. ↵
    Snyder WS, Fisher HL, Ford MR, Warner GG. Estimates of absorbed fractions for monoenergetic photon sources uniformly distributed in various organs of a heterogeneous phantom. J Nucl Med. 1969;10(suppl):7S–52S.
    OpenUrl
  6. ↵
    Snyder WS, Ford MR, Warner GG. Estimates of Specific Absorbed Fractions for Photon Sources Uniformly Distributed in Various Organs of a Heterogeneous Phantom. MIRD Pamplet No. 5, rev. New York, NY: Society of Nuclear Medicine; 1978.
  7. ↵
    Snyder WS, Ford MR, Warner GG, Watson SB. “S” Absorbed Dose Per Unit Cumulated Activity for Selected Radionuclides and Organs. MIRD Pamphlet No. 11. New York, NY: Society of Nuclear Medicine; 1975.
  8. ↵
    Cristy M, Eckerman KF. Specific Absorbed Fractions of Energy at Various Ages for Internal Photon Sources. ORNL/TM-8381. Oak Ridge, TN: Oak Ridge National Laboratory; 1987.
  9. ↵
    Zanzonico PB. Internal radionuclide radiation dosimetry: a review of basic concepts and recent developments. J Nucl Med. 2000;41:297–308.
    OpenUrlAbstract/FREE Full Text
  10. ↵
    Watson EE, Stabin MG, Davis JL, Eckerman KF. A model of the peritoneal cavity for use in internal dosimetry. J Nucl Med. 1989;30:2002–2011.
    OpenUrlAbstract/FREE Full Text
  11. Stabin MG. A model of the prostate gland for use in internal dosimetry. J Nucl Med. 1994;35:516–520.
    OpenUrlAbstract/FREE Full Text
  12. Bouchet LG, Bolch WE, Weber DA, Atkins HL, Poston JW Sr. MIRD pamphlet no. 15: radionuclide S values in a revised dosimetric model of the adult head and brain. J Nucl Med. 1999;40:62S–101S.
  13. Mardirossian G, Tagesson M, Blanco P, et al. A new rectal model for dosimetry applications. J Nucl Med. 1999;40:1524–1531.
    OpenUrlAbstract/FREE Full Text
  14. Bouchet LG, Bolch WE, Howell RW, Rao DV. S values for radionuclides localized within the skeleton. J Nucl Med. 2000;41:189–212.
    OpenUrlAbstract/FREE Full Text
  15. ↵
    Bouchet LG, Bolch WE, Blanco HP, et al. MIRD pamphlet no. 19: absorbed fractions and radionuclide S values for 6 age-dependent multiregion models of the kidney. J Nucl Med. 2003;44:1113–1147.
    OpenUrlAbstract/FREE Full Text
  16. ↵
    Goddu SM, Howell RW, Rao DV. Cellular dosimetry: absorbed fractions for monoenergetic electron and alpha particle sources and S-values for radionuclides uniformly distributed in different cell compartments. J Nucl Med. 1994;35:303–316.
    OpenUrlAbstract/FREE Full Text
  17. ↵
    Goddu SM, Howell RL, Bouchet LG, Bolch WE, Rao DV. MIRD Cellular S Values. Reston, VA: Society of Nuclear Medicine; 1997.
  18. ↵
    Bolch WE, Bouchet LG, Robertson JS, et al. MIRD pamphlet no. 17: the dosimetry of nonuniform activity distributions-radionuclide S values at the voxel level. J Nucl Med. 1999;40:11S–36S.
  19. ↵
    Williams LE, Liu A, Raubitschek AA, Wong JY. A method for patient-specific absorbed dose estimation for internal beta emitters. Clin Cancer Res. 1999;5:3015s–3019s.
  20. ↵
    McKay E. A software tool for specifying voxel models for dosimetry estimation. Cancer Biother Radiopharm. 2003;18:379–392.
    OpenUrlCrossRefPubMed
  21. ↵
    Guy MJ, Flux GD, Papavasileiou P, Flower MA, Ott RJ. RMDP: a dedicated package for 131I SPECT quantification, registration and patient-specific dosimetry. Cancer Biother Radiopharm. 2003;18:61–69.
    OpenUrlCrossRefPubMed
  22. ↵
    Stabin MG. MIRDOSE: personal computer software for internal dose assessment in nuclear medicine. J Nucl Med. 1996;37:538–546.
    OpenUrlFREE Full Text
  23. ↵
    Johnson TK, McClure D, McCourt S. MABDOSE. I: characterization of a general purpose dose estimation code. Med Phys. 1999;26:1389–1395.
    OpenUrlPubMed
  24. ↵
    Johnson TK, McClure D, McCourt S. MABDOSE. II: validation of a general purpose dose estimation code. Med Phys. 1999;26:1396–1403.
    OpenUrlPubMed
  25. ↵
    Sgouros G, Barest G, Thekkumthala J, et al. Treatment planning for internal radionuclide therapy: three-dimensional dosimetry for nonuniformly distributed radionuclides. J Nucl Med. 1990;31:1884–1891.
    OpenUrlAbstract/FREE Full Text
  26. Giap HB, Macey DJ, Bayouth JE, Boyer AL. Validation of a dose-point kernel convolution technique for internal dosimetry. Phys Med Biol. 1995;40:365–381.
    OpenUrlCrossRefPubMed
  27. Giap HB, Macey DJ, Podoloff DA. Development of a SPECT-based three-dimensional treatment planning system for radioimmunotherapy. J Nucl Med. 1995;36:1885–1894.
    OpenUrlAbstract/FREE Full Text
  28. Furhang EE, Sgouros G, Chui CS. Radionuclide photon dose kernels for internal emitter dosimetry. Med Phys. 1996;23:759–764.
    OpenUrlCrossRefPubMed
  29. ↵
    Flux GD, Webb S, Ott RJ, Chittenden SJ, Thomas R. Three-dimensional dosimetry for intralesional radionuclide therapy using mathematical modeling and multimodality imaging. J Nucl Med. 1997;38:1059–1066.
    OpenUrlAbstract/FREE Full Text
  30. ↵
    Kolbert KS, Sgouros G, Scott AM, et al. Implementation and evaluation of patient-specific three-dimensional internal dosimetry. J Nucl Med. 1997;38:301–308.
    OpenUrlAbstract/FREE Full Text
  31. ↵
    Erdi AK, Yorke ED, Loew MH, et al. Use of the fast Hartley transform for three-dimensional dose calculation in radionuclide therapy. Med Phys. 1998;25:2226–2233.
    OpenUrlPubMed
  32. ↵
    Furhang EE, Chui CS, Sgouros G. A Monte Carlo approach to patient-specific dosimetry. Med Phys. 1996;23:1523–1529.
    OpenUrlCrossRefPubMed
  33. ↵
    Tagesson M, Ljungberg M, Strand SE. A Monte-Carlo program converting activity distributions to absorbed dose distributions in a radionuclide treatment planning system. Acta Oncol. 1996;35:367–372.
    OpenUrlPubMed
  34. ↵
    Furhang EE, Chui CS, Kolbert KS, Larson SM, Sgouros G. Implementation of a Monte Carlo dosimetry method for patient-specific internal emitter therapy. Med Phys. 1997;24:1163–1172.
    OpenUrlCrossRefPubMed
  35. Liu A, Williams LE, Wong JY, Raubitschek AA. Monte Carlo-assisted voxel source kernel method (MAVSK) for internal beta dosimetry. Nucl Med Biol. 1998;25:423–433.
    OpenUrlCrossRefPubMed
  36. ↵
    Clairand I, Ricard M, Gouriou J, Di Paola M, Aubert B. DOSE3D: EGS4 Monte Carlo code-based software for internal radionuclide dosimetry. J Nucl Med. 1999;40:1517–1523.
    OpenUrlAbstract/FREE Full Text
  37. Yoriyaz H, dos Santos A, Stabin MG, Cabezas R. Absorbed fractions in a voxel-based phantom calculated with the MCNP-4B code. Med Phys. 2000;27:1555–1562.
    OpenUrlCrossRefPubMed
  38. Yoriyaz H, Stabin MG, dos SA. Monte Carlo MCNP-4B-based absorbed dose distribution estimates for patient-specific dosimetry. J Nucl Med. 2001;42:662–669.
    OpenUrlAbstract/FREE Full Text
  39. ↵
    Descalle MA, Hartmann Siantar CL, Dauffy L, et al. Application of MINERVA Monte Carlo simulations to targeted radionuclide therapy. Cancer Biother Radiopharm. 2003;18:71–79.
    OpenUrlCrossRefPubMed
  40. ↵
    Sgouros G, Kolbert KS. The three-dimensional internal dosimetry software package, 3D-ID. In: Zaidi H, Sgouros G, eds. Therapeutic Applications of Monte Carlo Calculations in Nuclear Medicine. Philadelphia, PA: Institute of Physics; 2002.
  41. ↵
    Sgouros G, Chiu S, Pentlow KS, et al. Three-dimensional dosimetry for radioimmunotherapy treatment planning. J Nucl Med. 1993;34:1595–1601.
    OpenUrlAbstract/FREE Full Text
  42. ↵
    Sgouros G, Squeri S, Ballangrud AM, et al. Patient-specific, 3-dimensional dosimetry in non-Hodgkin’s lymphoma patients treated with 131I-anti-B1 antibody: assessment of tumor dose-response. J Nucl Med. 2003;44:260–268.
    OpenUrlAbstract/FREE Full Text
  43. ↵
    Sgouros G, Kolbert KS, Sheikh A, et al. Patient-specific dosimetry for 131I thyroid cancer therapy using 124I PET and 3-dimensional-internal dosimetry (3D-ID) software. J Nucl Med. 2004;45:1366–1372.
    OpenUrlAbstract/FREE Full Text
  44. ↵
    Kolbert KS, Sgouros G, Scott AM, et al. Dose-volume histogram representation of patient dose distribution in 3-dimensional internal dosimetry [abstract]. J Nucl Med. 1994;35:P123–P124.
    OpenUrl
  45. ↵
    Koral KF, Francis IR, Kroll S, et al. Volume reduction versus radiation dose for tumors in previously untreated lymphoma patients who received iodine-131 tositumomab therapy. Conjugate views compared with a hybrid method. Cancer. 2002;94:1258–1263.
    OpenUrlCrossRefPubMed
  46. ↵
    Ljungberg M, Sjogreen K, Liu X, et al. A 3-dimensional absorbed dose calculation method based on quantitative SPECT for radionuclide therapy: evaluation for 131I using Monte Carlo simulation. J Nucl Med. 2002;43:1101–1109.
    OpenUrlAbstract/FREE Full Text
  47. ↵
    Ljungberg M, Frey E, Sjogreen K, et al. 3D absorbed dose calculations based on SPECT: evaluation for 111-In/90-Y therapy using Monte Carlo simulations. Cancer Biother Radiopharm. 2003;18:99–107.
    OpenUrlCrossRefPubMed
  48. ↵
    Siegel JA, Wessels B, Watson EE, et al. Bone marrow dosimetry and toxicity for radioimmunotherapy. Antibody Immunoconj Radiopharm. 1990;3:213–233.
    OpenUrl
  49. ↵
    Sgouros G. Bone marrow dosimetry for radioimmunotherapy: theoretical considerations. J Nucl Med. 1993;34:689–694.
    OpenUrlAbstract/FREE Full Text
  50. Shen S, DeNardo GL, Sgouros G, O’Donnell RT, DeNardo SJ. Practical determination of patient-specific marrow dose using radioactivity concentration in blood and body. J Nucl Med. 1999;40:2102–2106.
    OpenUrlAbstract/FREE Full Text
  51. ↵
    Sgouros G, Stabin M, Erdi Y, et al. Red marrow dosimetry for radiolabeled antibodies that bind to marrow, bone, or blood components. Med Phys. 2000;27:2150–2164.
    OpenUrlCrossRefPubMed
  52. Stabin MG, Siegel JA, Sparks RB. Sensitivity of model-based calculations of red marrow dosimetry to changes in patient-specific parameters. Cancer Biother Radiopharm. 2002;17:535–543.
    OpenUrlPubMed
  53. ↵
    Behr TM, Behe M, Sgouros G. Correlation of red marrow radiation dosimetry with myelotoxicity: empirical factors influencing the radiation-induced myelotoxicity of radiolabeled antibodies, fragments and peptides in pre-clinical and clinical settings. Cancer Biother Radiopharm. 2002;17:445–464.
    OpenUrlCrossRefPubMed
  54. Hindorf C, Linden O, Tennvall J, Wingardh K, Strand SE. Time dependence of the activity concentration ratio of red marrow to blood and implications for red marrow dosimetry. Cancer. 2002;94:1235–1239.
    OpenUrlPubMed
  55. ↵
    Shen S, Meredith RF, Duan J, et al. Comparison of methods for predicting myelotoxicity for non-marrow targeting I-131-antibody therapy. Cancer Biother Radiopharm. 2003;18:209–215.
    OpenUrlCrossRefPubMed
  56. ↵
    Sharkey RM, Brenner A, Burton J, et al. Radioimmunotherapy of non-Hodgkin’s lymphoma with 90Y-DOTA humanized anti-CD22 IgG (90Y-Epratuzumab): do tumor targeting and dosimetry predict therapeutic response? J Nucl Med. 2003;44:2000–2018.
    OpenUrlAbstract/FREE Full Text
  57. ↵
    Cartron G, Dacheux L, Salles G, et al. Therapeutic activity of humanized anti-CD20 monoclonal antibody and polymorphism in IgG Fc receptor FcgammaRIIIa gene. Blood. 2002;99:754–758.
    OpenUrlAbstract/FREE Full Text
  58. ↵
    Meredith R, Shen S, Macey D, et al. Comparison of biodistribution, dosimetry, and outcome from clinical trials of radionuclide-CC49 antibody therapy. Cancer Biother Radiopharm. 2003;18:393–404.
    OpenUrlCrossRefPubMed
  59. ↵
    Siegel JA, Thomas SR, Stubbs JB, et al. MIRD pamphlet no. 16: techniques for quantitative radiopharmaceutical biodistribution data acquisition and analysis for use in human radiation dose estimates. J Nucl Med. 1999;40:37S–61S.
  60. ↵
    Pauwels S, Barone R, Walrand S. Practical dosimetry of peptide receptor radionuclide therapy with 90Y-labeled somatostatin analogues. J Nucl Med. 2005;46(suppl):92S–98S.
    OpenUrlAbstract/FREE Full Text
  61. ↵
    Wessels BW, Bolch WE, Bouchet LG, et al. Bone marrow dosimetry for radionuclide therapy: A multi-institutional comparison. J Nucl Med. 2004;45:1725–1733.
    OpenUrlAbstract/FREE Full Text
  62. Zanzonico P, Sgouros G. Predicting myelotoxicity in radioimmunotherapy: what does dosimetry contribute? J Nucl Med. 1997;38:1753–1754.
    OpenUrlFREE Full Text
  63. Goddu SM, Howell RW, Giuliani DC, Rao DV. Biological dosimetry of bone marrow for incorporated yttrium-90. J Nucl Med. 1998;39:547–552.
    OpenUrlAbstract/FREE Full Text
  64. Breitz HB, Fisher DR, Wessels BW. Marrow toxicity and radiation absorbed dose estimates from rhenium-186-labeled monoclonal antibody. J Nucl Med. 1998;39:1746–1751.
    OpenUrlAbstract/FREE Full Text
  65. Wong JY, Wang J, Liu A, et al. Evaluating changes in stable chromosomal translocation frequency in patients receiving radioimmunotherapy. Int J Radiat Oncol Biol Phys. 2000;46:599–607.
    OpenUrlPubMed
  66. Lenarczyk M, Goddu SM, Rao DV, Howell RW. Biologic dosimetry of bone marrow: induction of micronuclei in reticulocytes after exposure to 32P and 90Y. J Nucl Med. 2001;42:162–169.
    OpenUrlAbstract/FREE Full Text
  67. ↵
    O’Donoghue JA, Baidoo N, Deland D, et al. Hematologic toxicity in radioimmunotherapy: dose-response relationships for I-131 labeled antibody therapy. Cancer Biother Radiopharm. 2002;17:435–443.
    OpenUrlCrossRefPubMed
  68. ↵
    Wahl RL, Kroll S, Zasadny KR. Patient-specific whole-body dosimetry: principles and a simplified method for clinical implementation. J Nucl Med. 1998;39(suppl):14S–20S.
  69. ↵
    Wahl RL. The clinical importance of dosimetry in radioimmunotherapy with tositumomab and iodine I-131 tositumomab. Semin Oncol. 2003;30:31–38.
    OpenUrlPubMed
  70. ↵
    Wiseman GA, Leigh B, Erwin WD, et al. Radiation dosimetry results for Zevalin radioimmunotherapy of rituximab-refractory non-Hodgkin lymphoma. Cancer. 2002;94:1349–1357.
    OpenUrlCrossRefPubMed
  71. ↵
    Wiseman GA, Kornmehl E, Leigh B, et al. Radiation dosimetry results and safety correlations from 90Y-ibritumomab tiuxetan radioimmunotherapy for relapsed or refractory non-Hodgkin’s lymphoma: combined data from 4 clinical trials. J Nucl Med. 2003;44:465–474.
    OpenUrlAbstract/FREE Full Text
  72. ↵
    Siegel JA, Yeldell D, Goldenberg DM, et al. Red marrow radiation dose adjustment using plasma FLT3-L cytokine levels: improved correlations between hematologic toxicity and bone marrow dose for radioimmunotherapy patients. J Nucl Med. 2003;44:67–76.
    OpenUrlAbstract/FREE Full Text
  73. ↵
    Jokisch DW, Patton PW, Inglis BA, et al. NMR microscopy of trabecular bone and its role in skeletal dosimetry. Health Phys. 1998;75:584–596.
    OpenUrlPubMed
  74. Bouchet LG, Jokisch DW, Bolch WE. A three-dimensional transport model for determining absorbed fractions of energy for electrons within trabecular bone. J Nucl Med. 1999;40:1947–1966.
    OpenUrlAbstract/FREE Full Text
  75. Rajon DA, Jokisch DW, Patton PW, Shah AP, Bolch WE. Voxel size effects in three-dimensional nuclear magnetic resonance microscopy performed for trabecular bone dosimetry. Med Phys. 2000;27:2624–2635.
    OpenUrlPubMed
  76. Jokisch DW, Patton PW, Rajon DA, Inglis BA, Bolch WE. Chord distributions across 3D digital images of a human thoracic vertebra. Med Phys. 2001;28:1493–1504.
    OpenUrlPubMed
  77. Bolch WE, Patton PW, Rajon DA, et al. Considerations of marrow cellularity in 3-dimensional dosimetric models of the trabecular skeleton. J Nucl Med. 2002;43:97–108.
    OpenUrlAbstract/FREE Full Text
  78. Rajon DA, Jokisch DW, Patton PW, et al. Voxel effects within digital images of trabecular bone and their consequences on chord-length distribution measurements. Phys Med Biol. 2002;47:1741–1759.
    OpenUrlPubMed
  79. Rajon DA, Patton PW, Shah AP, Watchman CJ, Bolch WE. Surface area overestimation within three-dimensional digital images and its consequence for skeletal dosimetry. Med Phys. 2002;29:682–693.
    OpenUrlPubMed
  80. Stabin MG, Eckerman KF, Bolch WE, Bouchet LG, Patton PW. Evolution and status of bone and marrow dose models. Cancer Biother Radiopharm. 2002;17:427–433.
    OpenUrlCrossRefPubMed
  81. Shah AP, Patton PW, Rajon DA, Bolch WE. Adipocyte spatial distributions in bone marrow: implications for skeletal dosimetry models. J Nucl Med. 2003;44:774–783.
    OpenUrlAbstract/FREE Full Text
  82. Rajon DA, Bolch WE. Marching cube algorithm: review and trilinear interpolation adaptation for image-based dosimetric models. Comput Med Imaging Graph. 2003;27:411–435.
    OpenUrlCrossRefPubMed
  83. ↵
    Rajon DA, Shah AP, Watchman CJ, Brindle JM, Bolch WE. A hyperboliod representation of the bone-marrow interface within 3D NMR images of trabecular bone: applications to skeletal dosimetry. Phys Med Biol. 2003;48:1721–1740.
    OpenUrlPubMed
  84. ↵
    Moll S, Nickeleit V, Mueller-Brand J, et al. A new cause of renal thrombotic microangiopathy: yttrium 90-DOTATOC internal radiotherapy. Am J Kidney Dis. 2001;37:847–851.
    OpenUrlPubMed
  85. Cybulla M, Weiner SM, Otte A. End-stage renal disease after treatment with 90Y-DOTATOC. Eur J Nucl Med. 2001;28:1552–1554.
    OpenUrlCrossRefPubMed
  86. ↵
    De Jong M, Valkema R, Jamar F, et al. Somatostatin receptor-targeted radionuclide therapy of tumors: preclinical and clinical findings. Semin Nucl Med. 2002;32:133–140.
    OpenUrlCrossRefPubMed
  87. Otte A, Weiner SM, Cybulla M. Is radiation nephropathy caused by yttrium-90? Lancet. 2002;359:979.
    OpenUrl
  88. ↵
    Giralt S, Bensinger W, Goodman M, et al. Ho-166-DOTMP plus melphalan followed by peripheral blood stem cell transplantation in patients with multiple myeloma: results of two phase 1/2 trials. Blood. 2003;102:2684–2691.
    OpenUrlAbstract/FREE Full Text
  89. ↵
    Lambert B, Cybulla M, Weiner SM, et al. Renal toxicity after radionuclide therapy. Radiat Res. 2004;161:607–611.
    OpenUrlCrossRefPubMed
  90. ↵
    Russeva MG, Adams GP. Radioimmunotherapy with engineered antibodies. Expert Opinion Biol Ther. 2004;4:217–231.
  91. ↵
    Emami B, Lyman J, Brown A, et al. Tolerance of normal tissue to therapeutic irradiation. Int J Radiat Oncol Biol Phys. 1991;21:109–122.
    OpenUrlPubMed
  92. ↵
    Behr TM, Behe M, Angerstein C, et al. Cholecystokinin-B/gastrin receptor binding peptides: preclinical development and evaluation of their diagnostic and therapeutic potential. Clin Cancer Res. 1999;5:3124s–3138s.
  93. ↵
    Breitz H, Wendt R, Stabin M, Bouchet L, Wessels B. Dosimetry of High Dose Skeletal Targeted Radiotherapy (STR) with (166)Ho-DOTMP. Cancer Biother Radiopharm. 2003;18:225–230.
    OpenUrlCrossRefPubMed
  94. ↵
    Wessels B. Summary and perspectives on kidney dose-response to radionuclide therapy. Cancer Biother Radiopharm. 2004;19:388–390.
    OpenUrlCrossRefPubMed
  95. ↵
    Dale R. Use of the linear-quadratic radiobiological model for quantifying kidney response in targeted radiotherapy. Cancer Biother Radiopharm. 2004;19:363–370.
    OpenUrlCrossRefPubMed
  96. Sgouros G. Introduction to kidney dose-response for radionuclide therapy. Cancer Biother Radiopharm. 2004;19:357–358.
    OpenUrlPubMed
  97. ↵
    Breitz H. Clinical aspects of radiation nephropathy. Cancer Biother Radiopharm. 2004;19:359–362.
    OpenUrlCrossRefPubMed
  98. O’Donoghue J. Relevance of external beam dose-response relationships to kidney toxicity associated with radionuclide therapy. Cancer Biother Radiopharm. 2004;19:378–387.
    OpenUrlCrossRefPubMed
  99. ↵
    Green A, Flynn A, Pedley RB, Dearling J, Begent R. Nonuniform absorbed dose distribution in the kidney: the influence of organ architecture. Cancer Biother Radiopharm. 2004;19:371–377.
    OpenUrlCrossRefPubMed
  100. ↵
    Howell RW, Rao DV, Sastry KS. Macroscopic dosimetry for radioimmunotherapy: nonuniform activity distributions in solid tumors. Med Phys. 1989;16:66–74.
    OpenUrlCrossRefPubMed
  101. Humm JL, Cobb LM. Nonuniformity of tumor dose in radioimmunotherapy [comments]. J Nucl Med. 1990;31:75–83.
    OpenUrlAbstract/FREE Full Text
  102. Roberson PL, Heidorn DB, Kessler ML, Ten Haken RK, Buchsbaum DJ. Three-dimensional reconstruction of monoclonal antibody uptake in tumor and calculation of beta dose-rate nonuniformity. Cancer. 1994;73:912–918.
    OpenUrlPubMed
  103. Muthuswamy MS, Roberson PL, Ten Haken RK, Buchsbaum DJ. A quantitative study of radionuclide characteristics for radioimmunotherapy from 3D reconstructions using serial autoradiography. Int J Radiat Oncol Biol Phys. 1996;35:165–172.
    OpenUrlCrossRefPubMed
  104. ↵
    O’Donoghue JA. Implications of nonuniform tumor doses for radioimmunotherapy. J Nucl Med. 1999;40:1337–1341.
    OpenUrlAbstract/FREE Full Text
  105. O’Donoghue JA, Sgouros G, Divgi CR, Humm JL. Single-dose versus fractionated radioimmunotherapy: model comparisons for uniform tumor dosimetry. J Nucl Med. 2000;41:538–547.
    OpenUrlAbstract/FREE Full Text
  106. Flynn AA, Pedley RB, Green AJ, et al. Optimizing radioimmunotherapy by matching dose distribution with tumor structure using 3D reconstructions of serial images. Cancer Biother Radiopharm. 2001;16:391–400.
    OpenUrlPubMed
  107. Flynn AA, Pedley RB, Green AJ, et al. Antibody and radionuclide characteristics and the enhancement of the effectiveness of radioimmunotherapy by selective dose delivery to radiosensitive areas of tumour. Int J Radiat Biol. 2002;78:407–415.
    OpenUrlCrossRefPubMed
  108. ↵
    Flynn AA, Pedley RB, Green AJ, et al. The nonuniformity of antibody distribution in the kidney and its influence on dosimetry. Radiat Res. 2003;159:182–189.
    OpenUrlCrossRefPubMed
  109. ↵
    Barendsen GW. Dose fractionation, dose rate and iso-effect relationships for normal tissue responses. Int J Radiat Oncol Biol Phys. 1982;8:1981–1997.
    OpenUrlPubMed
  110. Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 1989;62:679–694.
    OpenUrlAbstract/FREE Full Text
  111. ↵
    Dale RG. Dose-rate effects in targeted radiotherapy. Phys Med Biol. 1996;41:1871–1884.
    OpenUrlCrossRefPubMed
  112. ↵
    Ling CC, Humm J, Larson S, et al. Towards multidimensional radiotherapy (MD-CRT): biological imaging and biological conformality. Int J Radiat Oncol Biol Phys. 2000;47:551–560.
    OpenUrlCrossRefPubMed
Back to top

In this issue

Print
Download PDF
Article Alerts
Email Article
Citation Tools
Bookmark this article

Jump to section

Related Articles

  • No related articles found.

Cited By...

More in this TOC Section

Similar Articles