Abstract
We present and validate a method to obtain an input function from dynamic image data and 0 or 1 blood sample for small-animal 18F-FDG PET studies. The method accounts for spillover and partial-volume effects via a physiologic model to yield a model-corrected input function (MCIF). Methods: Image-derived input functions (IDIFs) from heart ventricles and myocardial time–activity curves were obtained from 14 Sprague–Dawley rats and 17 C57BL/6 mice. Each MCIF was expressed as a mathematic equation with 7 parameters, which were estimated simultaneously with the myocardial model parameters by fitting the IDIFs and myocardium curves to a dual-output compartment model. Zero or 1 late blood sample was used in the simultaneous estimation. MCIF was validated by comparison with input measured from blood samples. Validation included computing errors in the areas under the curves (AUCs) and in the 18F-FDG influx constant Ki in 3 types of tissue. Results: For the rat data, the AUC error was 5.3% ± 19.0% in the 0-sample MCIF and −2.3% ± 14.8% in the 1-sample MCIF. When the MCIF was used to calculate the Ki of the myocardium, brain, and muscle, the overall errors were −6.3% ± 27.0% in the 0-sample method (correlation coefficient r = 0.967) and 3.1% ± 20.6% in the 1-sample method (r = 0.970). The t test failed to detect a significant difference (P > 0.05) in the Ki estimates from both the 0-sample and the 1-sample MCIF. For the mouse data, AUC errors were 4.3% ± 25.5% in the 0-sample MCIF and −1.7% ± 20.9% in the 1-sample MCIF. Ki errors averaged −8.0% ± 27.6% for the 0-sample method (r = 0.955) and −2.8% ± 22.7% for the 1-sample method (r = 0.971). The t test detected significant differences in the brain and muscle in the Ki for the 0-sample method but no significant differences with the 1-sample method. In both rat and mouse, 0-sample and 1-sample MCIFs both showed at least a 10-fold reduction in AUC and Ki errors compared with uncorrected IDIFs. Conclusion: MCIF provides a reliable, noninvasive estimate of the input function that can be used to accurately quantify the glucose metabolic rate in small-animal 18F-FDG PET studies.
PET with 18F-FDG is widely used to quantify glucose metabolism. This entails compartment modeling to estimate kinetic rate constants and requires knowledge of the input function, which is the 18F-FDG plasma time–activity curve (1,2). The gold standard to determine the input function is an invasive blood-sampling procedure to measure the 18F-FDG activity concentration in the arterial blood. For small-animal 18F-FDG PET studies, this procedure is challenging because of the small size of blood vessels and the limited blood volume. In addition, blood loss may perturb the physiology and confound the experimental outcome. To avoid these problems, various methods have been proposed to estimate the input function noninvasively. Those methods can be categorized as image-derived input functions (IDIFs), factor analysis (FA) methods, standardized input functions, and simultaneous estimation.
IDIFs are the time–activity curves obtained by drawing regions over the major vascular structures, such as the ventricular cavity, aorta, or large arteries (3). In principle, this method is relatively simple to use. However, in small-animal imaging, hearts and arteries are small compared with the scanner spatial resolution. Consequently, vascular radioactivity is blurred into adjacent tissues and vice versa. Also, cardiac and respiratory motion creates additional cross-contamination between vascular structures and surrounding tissues. As a result, curves obtained from regions drawn over the vascular space will be a mixture of the input function and the surrounding tissue time–activity curves. Some methods have been proposed to correct for the mixing—sometimes called spillover and partial-volume effect—in IDIFs using a few blood samples in clinical studies (4,5). For small-animal PET, Yee et al. applied the IDIF method to 15O-water studies with correction for partial volume and spillover (6). However, the assumption that the blood tracer concentration achieves equilibrium with that in the tissue makes the method inappropriate for 18F-FDG. Green et al. presented an IDIF in mice assuming a negligible contribution of the myocardium to the cavity curve (7). In many circumstances, this assumption is not valid.
FA methods have been applied to separate the arterial blood and the myocardial tissue components in the dynamic heart images. The heart image is assumed to be a sum of 3 or more factors—typically myocardium and blood in the left and right ventricles. Principal component analysis is applied to find these components and, therefore, obtain an estimate of the input function. FA has been used to extract the input function for rats and mice using just 1 blood sample (8), showing good correlation between the measured and extracted input functions. FA is described as being robust and requiring few blood samples. However, the ambiguity still exists in this method of whether, especially in mice (8), the factors found include the blood curves without spillover and partial-volume degradation. Moreover, an analysis of the consequence of using FA-derived input functions on the 18F-FDG influx rate constant has not been reported.
Standardized input function methods assume that input functions across animals and experimental conditions have an identical curve shape that can be used to approximate the individual input function by scaling the standard curve to match the concentration measured in 1 or 2 blood samples (9). In reality, the input function curve shape varies between subjects on the basis of several factors, such as the injection technique and speed, dietary state of the animal, metabolic status, catheterization site, and animal species. Therefore, the standard curve lacks the ability to account for the range of curve shapes present, especially in animals with abnormal metabolism. Moreover, the use of standardized input functions has not been validated for mice.
Simultaneous estimation was originally proposed to estimate the input function for human brain studies (10). It is assumed that the input function can be described by a mathematic function with multiple parameters that can be estimated simultaneously with the fitting of multiple regions of interest (ROIs), typically 3. Few, usually 2, late blood samples are required in the simultaneous estimation process. The main challenge of this method is the large number of parameters (>25) that needs to be estimated, thus making the fitting especially challenging. Moreover, this method has not been validated in small-animal PET studies.
In this article we present and validate a method that overcomes the limitations of the above methods. Our method uses simultaneous estimation to correct the spillover and partial-volume effect for an IDIF. We assume that both the IDIF from the heart ventricles and the time–activity curve of the myocardium are mixtures of the true input function and the myocardium uptake. Using a mathematic equation to express the input function, we can then determine both time–activity curves as outputs of a compartment model simultaneously with the nonvascular tissue parameters. The estimated input is denoted as a model-corrected input function (MCIF) because it is obtained by correcting the spillover and partial-volume effects from IDIF by compartment modeling. This method is validated by comparing the MCIF estimated with 0 or 1 blood sample with the input functions measured with blood sampling in rats and mice. We also compared our MCIF with the uncorrected IDIF.
MATERIALS AND METHODS
Rat Studies
All experiments took place in the Case Center for Imaging Research in Case Western Reserve University and were performed according to a protocol approved by its Institutional Animal Care and Use Committee. Twenty datasets were acquired from 14 female Sprague–Dawley rats ranging from 206 to 253 g. Six of the 14 underwent 2 studies separated by 1 wk. For each scan, the rat was anesthetized with 2%∼2.5% isoflurane in oxygen. Each rat was cannulated in the tail artery with microrenathane tubing (0.83-mm outer diameter) and in the tail vein with microrenathane tubing (0.63-mm outer diameter). Each microPET study began with a 10-min transmission scan using a 57Co source on a microPET R4 scanner (Siemens Medical Solutions USA, Inc.). After that, a 90-min emission scan in 3-dimensional data-acquisition mode commenced with the intravenous bolus injection of approximately 30 MBq 18F-FDG. Dynamic image sequences were reconstructed with 5-s (n = 12), 30-s (n = 12), 60-s (n = 5), and 300-s (n = 17) frames. Fourier rebinning and a 2-dimensional filtered backprojection (FBP) algorithm was used for image reconstruction with 256 × 256 × 63 pixels per frame. Pixel spacing was 0.42 × 0.42 × 1.25 mm and the field of view included the brain, heart, and lung. Correction for radioactive decay, attenuation, scatter, and dead time was performed during the sinogram histogramming and reconstruction.
Blood sampling was performed to provide a gold-standard reference. For the first 3 min, a continuous automatic blood-sampling device, a blood-activity monitor (BAM), was used to acquire data with a high sampling rate to capture the initial rapid kinetics (11). During this time, the blood was continuously drawn from the arterial line using a syringe pump at 0.2 mL/min flow rate and counted by the BAM using contiguous 0.1-s intervals. After the first 3 min, continuous sampling was discontinued, and 10 samples were manually taken at 3.5, 4, 4.5, 5, 7, 10, 15, 30, 60, and 90 min. For 12 of the 20 studies, a late venous sample at 92 min was taken to compare the activity concentrations in late arterial and venous blood samples. The manual samples were counted with a well counter (Wallac LKB 1282). The sample net weight was measured to obtain the activity concentration from the counts. Input functions from the BAM and manual samples were linearly interpolated to construct a single input function. Shortly after the end of the study, an extra blood sample was taken for determination of the hematocrit and plasma activity fraction (plasma 18F-FDG divided by whole-blood 18F-FDG).
Mouse Studies
In addition to rat data, our method was tested using mouse data shared on the Internet by the Crump Institute of Molecular Imaging, UCLA (12,13). Seventeen C57BL/6 male mice weighing 22–36 g were anesthetized with 1.5%–2% isoflurane in oxygen. Of these, 9 mice were pretreated with insulin. As insulin does not directly affect the spillover and partial-volume effects, these data were treated as 1 group for evaluation of the input function estimation. Into each mouse, 9–37 MBq 18F-FDG were bolus-injected in the tail vein. Input functions were measured using femoral artery blood samples. On average, 15 (range, 5–22) samples were collected from each mouse. Eight mice were scanned with a microPET Focus-220 scanner and 9 were scanned with a microPET P4 scanner (both scanners: Siemens Medical Solutions USA, Inc.) For each PET study, a mouse underwent a CT scan for attenuation correction and then either a 60- or 90-min emission scan. Herein, only the first 60 min of data were used to standardize the data analysis. The image reconstruction method was FBP with 128 × 128 × 95 pixels. Dynamic framing varies slightly among these studies but typically there were 0.5-s (n = 15), 2-s (n = 1), 4-s (n = 1), 6-s (n = 1), 15-s (n = 1), 30-s (n = 3), 60-s (n = 1), 120-s (n = 1), 180-s (n = 3), and 900-s (n = 4) frames.
18F-FDG Compartment Model
The well-established compartment model has been used for estimating the rate constants and the glucose metabolic rate (1,2). This model entails 2 tissue compartments: 18F-FDG and phosphorylated 18F-FDG (18F-FDG-6P) in extravascular tissue, denoted by Ce and Cm, respectively. The state equations are: Eq. 1
Eq. 1 Eq. 2The model output equation is:
Eq. 2The model output equation is: Eq. 3where mi is the model-predicted activity concentration in the ith frame with the frame beginning at time
Eq. 3where mi is the model-predicted activity concentration in the ith frame with the frame beginning at time  and ending at time
and ending at time  Fv is the fraction of the pixel that is vascular space. Cp and Ca are the plasma and whole-blood time–activity curves, respectively. Cp is calculated from Ca by:
Fv is the fraction of the pixel that is vascular space. Cp and Ca are the plasma and whole-blood time–activity curves, respectively. Cp is calculated from Ca by: Eq. 4where H is the hematocrit and Fpa is the fraction of blood activity attributed to that in the plasma (plasma activity divided by whole-blood activity). Although there have been studies showing that the Fpa varies with time (14,15), accounting for this time variation requires blood sampling. In fact, many studies use whole blood as a surrogate for plasma activity and, therefore, implicitly assume that Fpa is constant. Thus, to simplify the procedure and offer the possibility of avoiding blood sampling, we treat Fpa as a constant (We observed Fpa to be 0.63 ± 0.07 in rats.). The glucose metabolic rate of glucose is defined by:
Eq. 4where H is the hematocrit and Fpa is the fraction of blood activity attributed to that in the plasma (plasma activity divided by whole-blood activity). Although there have been studies showing that the Fpa varies with time (14,15), accounting for this time variation requires blood sampling. In fact, many studies use whole blood as a surrogate for plasma activity and, therefore, implicitly assume that Fpa is constant. Thus, to simplify the procedure and offer the possibility of avoiding blood sampling, we treat Fpa as a constant (We observed Fpa to be 0.63 ± 0.07 in rats.). The glucose metabolic rate of glucose is defined by: Eq. 5LC is the lumped constant between 18F-FDG and glucose, and Cglu is the glucose concentration in blood. The 18F-FDG influx constant Ki equals
Eq. 5LC is the lumped constant between 18F-FDG and glucose, and Cglu is the glucose concentration in blood. The 18F-FDG influx constant Ki equals  Often determination of Ki alone is a sufficient index of glucose metabolism, and it can be robustly estimated. In contrast, obtaining precise estimates of k1 to k4 is less frequently used because of parameter correlation and noise in the time–activity curves. Therefore, our present work focuses on the estimates of Ki in the parameter estimation results.
Often determination of Ki alone is a sufficient index of glucose metabolism, and it can be robustly estimated. In contrast, obtaining precise estimates of k1 to k4 is less frequently used because of parameter correlation and noise in the time–activity curves. Therefore, our present work focuses on the estimates of Ki in the parameter estimation results.
Dual-Output Cardiac 18F-FDG Model
Ideally, when an ROI is drawn within the cavity of the left ventricle, the tissue time–activity curve would equal the whole-blood time–activity curve Ca. However, due to spillover and partial-volume effects, the model-predicted output of an IDIF is more accurately expressed as a mixture of blood and nonvascular tissue activity: Eq. 6where
Eq. 6where  is the mixing coefficient from the myocardium to the ventricular cavity, and
is the mixing coefficient from the myocardium to the ventricular cavity, and  is the mixing coefficient of the input function Ca. Similarly, the model output of the surrounding myocardium 18F-FDG concentration is:
is the mixing coefficient of the input function Ca. Similarly, the model output of the surrounding myocardium 18F-FDG concentration is: Eq. 7where
Eq. 7where  is the mixing coefficient from the tissue 18F-FDG uptake, and
is the mixing coefficient from the tissue 18F-FDG uptake, and  is the mixing coefficient of the input function Ca contribution to the myocardium ROI. If there is no spillover and partial-volume effect,
is the mixing coefficient of the input function Ca contribution to the myocardium ROI. If there is no spillover and partial-volume effect,  and
and  would equal 1, and
would equal 1, and 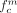 and
and  would equal 0. In microPET images, those 4 mixing coefficients range between 0 and 1, with
would equal 0. In microPET images, those 4 mixing coefficients range between 0 and 1, with  and
and  dominant (closer to 1) and greater than
dominant (closer to 1) and greater than  and
and  In this study, it is assumed that a single set of extravascular compartments (Ce, Cm) is adequate to predict both the ventricular (
In this study, it is assumed that a single set of extravascular compartments (Ce, Cm) is adequate to predict both the ventricular ( ) and the myocardial (
) and the myocardial ( ) activities because activities measured in these areas reflect a mixture of the same underlying myocardial extravascular and intravascular activities.
) activities because activities measured in these areas reflect a mixture of the same underlying myocardial extravascular and intravascular activities.
Simultaneous Estimation
Typical parameter estimation in compartment modeling assumes that both input and output are known, so that model parameters can be estimated by fitting the model output to the experimental data. Simultaneous estimation assumes, however, that the input is unknown but can be described by a model or an equation. Then, both the parameter sets of the input function and the tracer kinetic model can be estimated simultaneously by fitting model outputs to the experimental data. This entails accounting for the dependence of the model output on the input function parameters. In 18F-FDG PET studies, the input function Ca can be approximated by a 7-parameter equation (16): Eq. 8With Equation 8 and values for τ, A1∼A3, and L1∼L3, the input function can be approximated and carried into the model for solving the model output
Eq. 8With Equation 8 and values for τ, A1∼A3, and L1∼L3, the input function can be approximated and carried into the model for solving the model output  in Equation 6 with a given set of k1∼k4,
in Equation 6 with a given set of k1∼k4,  and
and  Model output
Model output  can be solved in the same way. Model outputs
can be solved in the same way. Model outputs  and
and  are then fit to the corresponding measurements, the PET measurement of 18F-FDG concentration in the ventricular cavity
are then fit to the corresponding measurements, the PET measurement of 18F-FDG concentration in the ventricular cavity  and in the myocardium
and in the myocardium , by minimizing the objective function:
, by minimizing the objective function: Eq. 9where p is the parameter vector [τ, A1, A2, A3. L1, L2, L3, k1, k2, k3, k4,
Eq. 9where p is the parameter vector [τ, A1, A2, A3. L1, L2, L3, k1, k2, k3, k4,  ] to be optimized. n is the total number of frames. w1 and w2 are weighting coefficients. If 1 blood sample is available to incorporate into the estimation process, the objective function can be extended to:
] to be optimized. n is the total number of frames. w1 and w2 are weighting coefficients. If 1 blood sample is available to incorporate into the estimation process, the objective function can be extended to: Eq. 10where b is the blood activity concentration at the sampling time ts. w3 is the weighting associated with the blood sample. The values of the weights w1∼w3 are estimated simultaneously with all other parameters using an extended least squares (ELS) method described by Muzic and Christian (17). The initial values and the lower and upper bounds of all parameters are summarized in Table 1. Once the simultaneous estimation is finished, the estimated values for parameters τ, A1∼A3, and L1∼L3 are used in Equation 8 to calculate the MCIF.
Eq. 10where b is the blood activity concentration at the sampling time ts. w3 is the weighting associated with the blood sample. The values of the weights w1∼w3 are estimated simultaneously with all other parameters using an extended least squares (ELS) method described by Muzic and Christian (17). The initial values and the lower and upper bounds of all parameters are summarized in Table 1. Once the simultaneous estimation is finished, the estimated values for parameters τ, A1∼A3, and L1∼L3 are used in Equation 8 to calculate the MCIF.
Initial Values and Bounds for Parameter Estimation to Obtain the MCIF
VOI and ROI Specification
Heart and myocardium ventricular volumes of interest (VOIs) were drawn for each animal on short-axis slices. When necessary, image volumes were rotated to obtain the short-axis view. A ventricular VOI consisted of 2-dimensional circular ROIs (n = 2–4) that were placed on the adjacent slices at the center of the heart ventricular cavity. Those ROIs were approximately 2.1 mm in diameter for rats and 1.6 mm for mice. A myocardium VOI was made of several 2-dimensional doughnut-like circular ROIs with hollow centers drawn on adjacent slices. The inner diameters of the myocardial ROIs were 4.2 mm for rats and 2.4 mm for mice. The outer diameters were 9.2 mm for rats and 5.2 mm for mice. Figure 1 shows an ROI on rat images. For validation by comparison of Ki values, brain and skeletal muscle ROIs were drawn for each animal.
Illustration of the typical placement of ventricular and myocardium ROIs. (A) The original axial view of rat chest. (B) View of heart after contrast adjustment. (C) The center ROI is the ventricular one. The area between the other 2 ROIs denotes myocardium.
Software and Computation Environments
All numeric analyses were done using MATLAB R2007a (Mathworks). COmpartment Model Kinetic Analysis Tool (COMKAT) (18), a kinetic modeling toolbox free for noncommercial use, was used for implementing the compartment models and fitting experimental data. The optimization was performed with COMKAT's fitGen function that uses MATLAB function “fmincon,” which is based on an interior-reflective Newton method (17,19).
Input Function Validation
How well an estimated input function approximated the measured input function was determined by direct and indirect methods. The direct method compared input functions by calculating the difference in areas under curves (AUCs) and the root mean square error (RMSE) of estimated input functions. The indirect comparison examined the impact of an estimated input function on the estimated tissue parameter Ki. Ki values in myocardium, brain, and muscle were calculated using a measured input function (Kimea) and an MCIF (Kiest). The error percentage of Ki was calculated as (Kiest − Kimea)/Kimea × 100 for each region and subject. These percent errors were summarized using mean and SD. Also, the correlation coefficients between Kimea and Kiest were calculated. A t test with α = 0.05 was used to examine if the Kimea and Kiest were significantly different in each region.
RESULTS
Results of the direct comparison between measured input functions, IDIF and MCIF, are summarized in Table 2. As shown in Figure 2, an IDIF without any correction is highly biased because of the spillover. Therefore, the AUC was highly biased and the RMSE was extremely high for the IDIF, as seen in Table 2. For example, the magnitude of AUC errors both in rats and mice exceeded 100%, meaning the AUC was more than double what it should have been. In contrast, under all conditions the MCIF had an AUC error of <6% bias for all conditions—rats and mice, 0 and 1 blood sample. With inclusion of 1 blood sample, this error was about 2%. Thus, compared with the IDIF, the MCIF reduces the AUC error by approximately 20-fold in rats and 100-fold in mice. In terms of RMSE, the MCIF achieved values of about 0.04 MBq/mL, which were much smaller than the 0.17- to 0.28-MBq/mL values obtained with the uncorrected IDIF. To illustrate the input function estimated with 0-sample MCIF compared with the measured input, Figure 3 shows a representative dataset from 1 rat. The input function is accurately estimated for both the early minutes and the whole study, as shown in Figures 3A and 3B, even when the initial guess of the input function parameters is far from the true values. Figure 3C demonstrates that the model output fits the IDIF and myocardium data very well. Figure 4 shows representative fitting results of 1 set of mouse data, indicating the close approximation of the MCIF to the measured input.
Comparison between measured input function (solid line) and IDIF (dashed line) in 1 rat shows that the IDIF is higher than the measured input, primarily due to spillover from myocardium 18F-FDG activity.
Estimation plots of 1 rat with the 0-sample MCIF estimation. (A) Measured input function (circles) and estimated input with the 0-sample MCIF method (solid line) for first 3 min. (B) Measured input function (circles) and estimated input with the 0-sample MCIF method (solid line) for entire scan duration. (C) Measured and model-predicted time–activity curves for IDIF and myocardium uptake. In both A and B, estimated input functions show a good agreement with the measured one. C indicates that the dual-output model can fit the data well.
Estimation results of 1 mouse with the 0-sample MCIF estimation. (A) Measured input function (circles) and estimated input with 0-sample MCIF method (solid line) for first 3 min. (B) Measured input function (circles) and estimated input with 0-sample MCIF method (solid line) for entire scan duration. (C) Measured and model-predicted time–activity curves for IDIF and myocardium uptake.
Direct Comparison of Estimated Input Functions
As the purpose to estimate the input function is for its use in compartment modeling, evaluating how much error is introduced in the estimates of Ki is especially important. Table 3 lists the comparison of Ki values obtained from various input functions. When an IDIF without any correction was used in estimating Ki, the estimation of Ki was highly biased compared with the reference Ki values obtained using the measured input. This is due to the IDIF itself being highly biased, as shown in the direct comparison described earlier. In contrast, the MCIF greatly reduced the bias in the Ki estimates. For rats, the overall error percentage of Ki of all 3 regions averaged 6.3% ± 27.0% for 0-sample MCIF and −3.1% ± 20.6% for 1-sample MCIF, with correlation coefficients of 0.967 and 0.970, respectively. The t test failed to detect a significant difference in all 3 types of tissue using either 0-sample or 1-sample MCIF (P > 0.05). Comparing the 0-sample and 1-sample MCIF methods, the 1-sample MCIF methods reduced Ki bias in both the brain and the muscle but slightly increased it in the myocardium. The precision was also greatly improved in the brain and muscle. Correlation coefficients increased in all 3 regions with the 1-sample MCIF. Figure 5 shows a box plot of the Ki error in 0- and 1-sample MCIF. Including 1 blood sample brought the median value closer to 0 and reduced the interquartile range (IQR). Taken together, these results show that the MCIF performs well in the tasks of estimating the input function and Ki, greatly reducing the error for IDIFs.
Box plot of Ki error percentage of the 0-sample and 1-sample MCIF estimation for rat data. Box height shows interquartile range (IQR). Median is shown as the line in the box. Whiskers indicate the quartile bounds ± 1.5 × IQR. Outliers that exceed this range are indicated by circles. For visual clarity, results from IDIF are not shown on this plot because the Ki with IDIF has a much higher error magnitude than the MCIF. In general, the heights of the boxes of the 1-sample MCIF are lower than those of the 0-sample MCIF. The error median is closer to 0 by the 1-sample MCIF.
Comparison of Ki Estimates from Measured and Estimated Input Functions from Rat Data (n = 20)
Similar results can be seen in the mouse data as listed in Table 4. Ki was again highly biased when using the IDIF without correction. With the MCIF, the overall error percentage of Ki of all 3 types of tissue was 8.0% ± 27.6% for the 0-sample and 2.8% ± 22.7% for the 1-sample MCIF method, with correlation coefficients of 0.955 and 0.971, respectively. Considering the individual tissue types, myocardium had the least bias and the best precision in Ki estimates. Although the correlation was high (r > 0.84) in all 3 types of tissue with the 0-sample MCIF, the t test detected significant biases in Ki estimates in brain and muscle (P < 0.05). These biases were resolved by the use of the 1-sample MCIF: The significant difference was not detected in any of the 3 regions. Moreover, use of 1 sample reduced the bias and improved the precision in brain and muscle and increased the correlation coefficients of all 3 regions to >0.9. The advantages of using the blood sample are visually evident in the box plot shown in Figure 6. In summary, with Ki analysis for MCIF in mice, bias and precision are better than that with IDIF. Inclusion of 1 blood sample improves MCIF such that no statistically significant bias was detected.
Box plot of Ki error percentage of the 0-sample and 1-sample MCIF estimation for mouse data. See Figure 5 legend for description of what the box height, center line, and whiskers indicate. Note significant reduction of IQR in the 1-sample MCIF. Also, the error median is closer to 0 in the 1-sample MCIF.
Comparison of Ki Estimates from Measured and Estimated Input Functions from Mouse Data (n = 17)
As a less invasive alternative to using 1 late arterial blood sample, we considered substituting activity concentration in a venous sample as an approximation to that in an arterial sample. In rats, venous activity concentration differed from arterial activity concentration by −5.8% ± 13.0%. Regression analysis showed a correlation coefficient of 0.944 (y = 0.942·x + 0.019, where y is the arterial activity concentration and x is the venous activity concentration), indicating that the late venous activity concentration is very close to the arterial concentration.
DISCUSSION
The ability to quantify physiologic function with measurable and testable results in a reliable and practical manner is crucial to research. In this regard, compartment modeling has long been regarded as one of the best ways to analyze PET images. However, the blood-sampling procedure to measure the input function in small animals has been a major barrier because of its invasive nature, the small size of blood vessels, and the animals' limited blood volume. Although new and advanced devices have been proposed to measure the blood activity—such as microfluidic blood-sampling devices (15) and blood-activity monitors (20)—an invasive surgery procedure is required, making it difficult for imaging centers to include the technically demanding procedure in routine PET studies. Obtaining the input function from images using IDIFs or FA is a popular alternative as it can be done without blood sampling. IDIFs have the advantage of simplicity over FA methods but the spillover and partial-volume effects make the IDIF a highly biased estimate. Therefore, we sought to find a practical and robust method to correct for the spillover and partial-volume effect in IDIF by using simultaneous estimation to determine and correct the cross-contamination between ventricular and myocardial activities.
We compared the estimated input functions from MCIF with the inputs measured from blood samples. Our results show that the 1-sample MCIF is validated as a reliable method to estimate input functions and Ki constants. Using the extensive blood-sampling method as the reference, the AUC error of the 1-sample MCIF is <3% on average. Ki bias in both rats and mice is <10% and correlation coefficients are high. Most important, no significant difference was found by the t test in the 1-sample MCIF in both rats and mice, indicating that the 1-sample MCIF can be used as a replacement for input functions measured with extensive blood sampling. To use the 1-sample MCIF, a late venous sample, which is easy to collect, can be substituted for the arterial blood sample because late arterial and venous concentrations are very similar, as our results demonstrate. In addition, as the estimated MCIF is the whole-blood time–activity curve Ca, at least 1 blood sample must be taken to measure the hematocrit and activity fraction for conversion between Cp and Ca. This could provide the whole-blood concentration used for the simultaneous estimation in MCIF. Therefore, because 1 blood sample is simple to obtain and is necessary for hematocrit determination, we recommend using the 1-sample MCIF. On the other hand, although the 0-sample MCIF is not as accurate as 1-sample MCIF, its small bias did not reach statistical significance; thus, it may be applied in rat studies when blood sampling is infeasible or in retrospective analyses of data for which no blood samples were taken.
Compared with currently available methods for estimating input functions, MCIF has advantages. First, compared with IDIF, MCIF greatly reduces the bias by correcting for spillover and partial-volume effects. Second, compared with simultaneous estimation, MCIF has fewer parameters to estimate. Whereas the simultaneous estimation method first proposed by Wong et al. (10) models each tissue ROI according to an independent set of compartments, the MCIF method assumes that the measured heart ventricle and myocardium curves can be expressed as a weighted sum of the blood activity and the same underlying extravascular (Ce) and metabolized (Cm) activity concentrations. Consequently, only 2 VOIs and 1 set of k1∼k4 need to be estimated for MCIF with a total number of parameters to estimate 15, which is 10 fewer than the 25 required by the simultaneous estimation method of Wong et al. (10).
We speculate that MCIF will be improved with technologic advances. For example, cardiac and respiratory gating could reduce the spillover and partial-volume effects in the IDIF (21), therefore making MCIF more robust. Similarly, image reconstruction techniques, such as a maximum a posteriori (MAP) algorithm, that accurately model the γ-ray transport can produce images with better resolution, therefore reducing the spillover in the IDIF (22). Those methods can be used in combination with MCIF without any conflicts. When MCIF is applied to an IDIF with less severe spillover and partial volume, MCIF should be able to estimate the input function even more accurately.
Although the MCIF method is developed and validated using 18F-FDG, the methodology should be applicable to other PET tracers. In particular, the output equation of the heart ventricles and myocardium would remain the same, and the configuration of the tracer kinetic model and parameter values, including initial values and bounds, would be adjusted. However, for tracers that require precise measurement of metabolites and for which a standard metabolite correction is not available, blood samples are inevitable. Otherwise, for other tracers it would be necessary to validate the adjustments in a study of a limited number of subjects wherein blood samples are collected and used for validation, as we have done here. Moreover, the MCIF should be applicable to human studies with similar adjustments and validation.
CONCLUSION
Herein, we show that the MCIF accurately accounts for spillover and partial-volume effect for IDIF and yields an input function suitable for use in quantifying glucose metabolic rate using the 18F-FDG model. Specifically, we show that either 0-sample or the 1-sample MCIF has AUC error, RMSE, and Ki estimation errors that are much lower than those obtained using the uncorrected IDIF. Furthermore, the use of 1 blood sample achieves a bias of Ki estimates to a level that is not statistically significant and that is lower than the uncertainty in the Ki estimates. Therefore, MCIF can be applied to 18F-FDG PET small-animal imaging for modeling analysis with a minimum blood-sampling requirement. The MCIF method is incorporated into the COMKAT toolbox and is available online at http://comkat.case.edu, free for noncommercial research use.
Acknowledgments
This work was supported by National Institute of Health grants R33-CA-101073 and R24-CA-110943. The authors thank Dr. Henry S.C. Huang and the Crump Institute of Molecular Imaging for the courtesy of sharing mouse data with us. We thank Chandra Spring Robinson and Deborah Barkauskas for assisting with the experiments and Dr. Mark Schluchter for discussions on statistics.
Footnotes
-
COPYRIGHT © 2008 by the Society of Nuclear Medicine, Inc.
References
- Received for publication September 27, 2007.
- Accepted for publication December 20, 2007.













