Automated 3-Dimensional Registration of Stand-Alone ¹⁸F-FDG Whole-Body PET with CT

MATERIALS AND METHODS

Registration Algorithm

The algorithm consists of several steps described below and a general overview is presented in Figure 1.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 1.

Flow chart with steps performed during automatic image registration.

Registration Cost Function.

We applied an MI-based technique (18) as a cost function and tested various implementations related to this method. The MI (19) estimates the statistical dependence of random variables. Perfectly aligned images will exhibit overlap of the features and, therefore, the overall information content in the combined, fused image will be reduced. This information reduction is greatest when the data are best aligned to each other. Therefore, we can try to maximize this reduction by varying the geometric transformation parameters of 1 volume (PET). The information reduction could be captured by finding the minimum of the joint entropy measure between 2 volumes, but such joint entropy is also dependent on the changing overlap of volumes (2). MI is less sensitive for these changes because it is defined as a difference between individual entropies and joint entropies (20).

Transformed PET data (both emission and transmission) and CT voxel intensities can be defined as random variables with marginal probability distributions pCT(c) and pPET(et) and a joint probability distribution pPETCT(et,c), where et are PET emission and transmission intensity values and c are the CT voxel intensity values; then the MI(PET,CT) between PET and CT, is defined as: Eq. 1 The joint probability distribution pPETCT(et,c) is defined as the probability of encountering voxel locations for which the intensity values are et in emission and transmission volumes and the CT values are c in the CT volume. The et value can refer to either emission or transmission voxel value or a combination of both. In addition, a modified normalized MI criterion (NMI) has been evaluated as proposed by Studholme et al. (21). This criterion was reported to be more successful than MI for the brain image registration due to lesser dependence on the variable overlap between volumes during registration. We have implemented this method because changing volume overlap was considered to be significant in our application (large misalignments along the axis of the bed and varying volume coverage). The NMI criterion was defined as: Eq. 2

To improve the computational efficiency and reduce the effect of the random noise in the calculation of the cost function, we reduced the number of the intensity levels to 100 in each modality and, therefore, the number of all intensity pairs was limited to 10,000, similar to our previous work (22). This reduction in the number of intensity bins assumes that the intensity variations of <1% are discarded in the calculation of the MI. The use of a larger number of bins did not have any significant effect on the registration as assessed in our preliminary evaluations. The joint probability is subsequently calculated by dividing the number of such voxel pairs (#) by the number of all voxels in the volume: Eq. 3 where X, Y, Z are the 3D dimensions of the volumes and x,y,z are the individual voxel indices.

The marginal probability distributions pPET(et) and pCT(c) are defined as the probabilities of encountering a particular intensity in each of the volumes (PET or CT), regardless of the corresponding voxel intensities in the other volume. They can be calculated as follows: Eq. 4 Eq. 5

Transmission maps acquired during PET scans for the purposes of attenuation correction can be used for the image registration (23,24). To reduce the dependence on the highly variable PET image characteristics, we have defined the cost function as a function of both transmission and emission scans, assuming both have been acquired in the same orientation. We have evaluated the registration using emission data alone (EM), transmission data alone (TR), and also using a combination of both emission and transmission data (TR+EM). In this implementation, the combination was achieved by addition of 2 volumes after normalization with a particular weighting function. To determine a suitable weighting factor we have attempted to maximize the number of successful registrations after image misalignment testing 3 different factors. The maximum number of successful registrations (95/100) was obtained for the weighting factor of 0.8 for emission and 0.2 for the transmission scan. Therefore, this weighting value was used in all subsequent experiments.

Minimization Algorithm for Linear Registration.

The automatic linear registration used a simplex-based minimization algorithm (25) to maximize the MI measure as defined above. To be able to use the minimization algorithm for maximization of the MI, the cost function was defined to be −MI(PET,CT) or −NMI(PET,CT). In minimizing the cost function, the simplex algorithm adjusted translations along the 3 coordinate axis (X shift, Y shift, and Z shift) and rotations within the 3 orthogonal planes (XY rotation, XZ rotation, and YZ rotation) as well as X, Y, and Z scalings, similar to the approach used by Hill et al. for correction of pixel scaling errors (26). In each iteration, PET volumes were resampled using trilinear interpolation. The iteration process was terminated when the relative decrease in the cost function was below a predefined threshold (<0.1%).

To improve the performance and reduce the possibility of entrapment in local minima, we used a multiresolution approach. The minimization process was repeated for PET and CT volumes rebinned to several matrix sizes, starting from the 32 × 32 matrix size. The search range was then progressively reduced for each cycle at a given image resolution. We evaluated the PET/CT registration algorithm with a different number of multiresolution steps.

Nonlinear Algorithm.

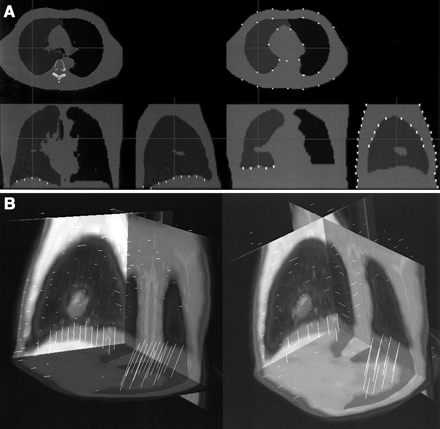
After linear registration with anisotropic linear scaling, we performed an additional step to correct for any remaining nonlinear differences. Lung voxels were automatically identified on PET transmission and CT volumes after linear registration using an adaptive threshold region-growing technique. Emission PET data were not used in the warping process. Second, all voxels inside the patient body were classified as lung or soft-tissue voxels. Subsequently, corresponding points on PET and CT lung outlines and external body outlines were identified by automatic ray tracing from centroids of the lungs and outside the body (Fig. 2A). In addition, spine voxels were identified on CT scans and assumed to be in the same location on the transmission scans (where spine is typically not clearly identifiable). The corresponding point pairs (ray points intersecting the CT and PET lung and body surfaces) formed 3D displacement vectors, which were then used as an input to the image warping module (Fig. 2B). To reduce image artifacts due to the incorrectly and inconsistently defined point pairs, we apply median filtering of vectors based on local neighborhoods. We assume that for each motion vector there exists a spheric neighborhood of a given radius, in which all motion vectors must have similar directions. This step avoids image artifacts caused by dissimilar motion vectors positioned close to each other.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 2.

Automatically identified landmarks on segmented CT (left) and segmented transmission map (right) identified by algorithm for nonlinear step (A) and resulting displacement vectors created by joining corresponding CT and transmission map landmarks (B).

Image Warping Method.

We use the TPS algorithm as described by Bookstein et al. (16) for nonlinear image warping based on the identified displacement vectors. This technique uses bicubic image interpolation and produces a smoothly interpolated deformation of the volume. To accelerate the performance we use a grid version of the TPS algorithm. The implementation of the arbitrary point pairs is represented as a grid deformation of a particular resolution. The implementation of this nonlinear image interpolation method has been recently described (27). A grid-based TPS transform allows for faster software implementation of the TPS.

RESULTS

During the reproducibility test of the linear registration, the use of emission data only (EM) resulted in 30 failures out of 100 as visually assessed (70% success rate). The use of transmission data (TR) resulted in 16 failures out of 100 (84% success rate). The use of the combination transmission and emission and data (TR+EM) resulted in 5 failures out of 100 (95% success rate) as determined visually. The reproducibility error of the registrations, for these 3 methods, has been evaluated quantitatively and the results are presented in Table 1. The reproducibility error was evaluated for the subset of the registration results, which have been determined as successful visually (to avoid bias by clearly failed results). The reproducibility error was similar for the TR+EM registration and TR registration but seems to be higher for the EM registration. We also did not observe difficulties in convergence of the algorithm when increasing the initial misalignment. Figures 3A and 3B show the errors in the translation parameters resulting from the initial translational misalignment and initial rotational misalignment, respectively, for the TR+EM MI registrations.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 3.

Errors in translational parameters after image registration as function of initial translational (A) and rotational (B) image misalignment.

Registration using the NMI criterion was converging faster than the MI criterion (n = 212 ± 92 iterations vs. 532 ± 92 iterations in 1 resolution pass). The number of failures that occurred during MI registration was 2 out of 50 (96% success). For the NMI registration, the number of failures was 5 out of 50 (90% success). Both MI and NMI were tested using a combined emission/transmission (TR+EM) registration. In addition, the reproducibility error of the registration using the MI criterion appeared to be better than the NMI-based registration for the combined emission/transmission registration (Table 2).

The use of the multiresolution registration algorithm resulted in the decrease of the registration time, despite the larger number of iterations (Table 3). The typical processing time on an Intel Pentium 2-GHz processor is <40 s. Please note that the specific results in Table 3 were obtained on a slower SPARC (Sun Microsystems) computer.

Multiresolution also improved the initial convergence and reproducibility of the registration (16/18 successfully registered datasets without multiresolution vs. 18/18 successfully registered datasets with multiresolution). On the basis of these results, the MI registration with multiresolution and with combined transmission/emission/data (TR+ EM) was selected as a method of choice before further nonlinear processing was applied.

The linear registration of all original 18 datasets using MI, multiresolution, and EM+TR combination was considered to be aligned automatically as close as possible to the correct position by translation, rotation, and scalings, as judged by the 2 observers. In 8 cases (3 normal breathing, 5 breath-hold), there was no visible diaphragm misregistration after applying the 9-parameter transformation. In the remaining 10 cases, there were evident nonlinear misregistration errors in the diaphragm area that were further corrected by the nonlinear algorithm. After application of the nonlinear algorithm, all registrations were judged successful. The differences between the original unregistered and registered positions were up to 20 pixels. The biggest differences were in the Z direction. Scaling parameters were adjusted up to 115%, the largest amount also in the Z direction.

Figure 4A represents the results of the linear registration with the CT acquired during deep breath-hold. In this case, the misalignment in the diaphragm area is evident and 9-parameter registration could not correct for the diaphragm displacement. Note large differences in the axial field-of-view extent between CT and PET, which has not caused difficulties for the automated registration algorithm. Figure 4B shows an example of the linear registration in the case of both CT and PET acquired during normal breathing, where no remaining nonlinear differences are visible.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 4.

Results of registration in case of deep-inspiration CT acquisition registered with normal-breathing PET (A) and normal breathing during CT and PET acquisition (B). In both cases, only linear registration module was used without warping correction.

Examples of corresponding point pairs identified by the ray tracing module are presented in Figure 2A on selected orthogonal slices of segmented CT and segmented transmission data and are also shown in 3D as warp vectors in Figure 2B. The maximum size of these 3D warp vectors between the linearly registered CT and PET scans was found by the algorithm to be 75 mm in the Z direction (diaphragm motion) and 42 mm in the axial planes (chest motion).

The median vector filtering technique eliminated the warping artifacts due to noncollinear warp vectors in close proximity to each other. Figure 5 illustrates the warping artifact before applying the median vector filtering (left) and the subsequent improvement of the alignment after the algorithm was applied (right). In addition to eliminating the artifacts, the filtering allowed reduction of the number of the point pairs, from the 270–400 range before filtering to the 225–365 range after filtering (on average, by 10%), which also resulted in the proportional decrease of the processing time. The nonlinear algorithm execution time is <30 s on a Pentium 2-GHz computer.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 5.

Example of warping artifact due to opposite displacement vectors in close proximity (left) and result of median filtering (right). Arrows indicate location of artifact.

The warping has been evaluated visually and judged successful in all 15 cases. In addition, lung volumes determined from segmented transmission and CT scans were calculated before and after the warp. Table 4 contains the transmission lung volume measurements compared with the CT lung volume measurements. The warped volumes match the CT volumes better, without a bias in the measurement, indicating correct selection of parameters for the lung segmentation.

For each case, the MI values were evaluated before and after warping. After warping, the MI cost function between the CT and warped PET TR volumes increased for all cases. The average increase in the cost function calculated after data warping, as compared with only linear registration, was 12%. This indicates that the image warping improved the statistical dependence of the matched datasets over the best value obtained with the linear registration.

The results of the image registration before and after warping, for 2 typical cases, are shown in Figure 6 (CT/PET transmission overlay) and Figure 7 (CT/PET emission overlay). In these 2 cases, there is a large mismatch in the diaphragm area when only linear registration has been applied. The linear registration results in the PET emission liver activity being placed in the lung area after fusion (Fig. 7, left). The nonlinear correction corrects this effect, which is shown with the warped transmission map (Fig. 6B) and with warped emission data (Fig. 7, right).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 6.

Final registration results in case of large diaphragmatic displacement shown on transmission–CT fusion images before warping (A) and after warping has been applied (B).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 7.

Final registration results in case shown on emission PET/CT fusion images before warping (left) and after warping applied (right).

DISCUSSION

Linear and nonlinear thoracic PET/CT registration has been attempted by some investigators previously. Yu et al. described a linear surface-based method using only the transmission scans (8). Nonlinear methods based on dividing the volume into several subvolumes have been proposed (11,13, 28). Our method is designed to perform with clinically acceptable speed, using accelerated techniques (multiresolution, accelerated warping). At the same time, the algorithm performs warping based on a large number of points, which allows a high degree of nonlinear deformations. In contrast to previous approaches, we use a 2-stage approach with clear distinction between the linear and nonlinear phase. The nonlinear phase could be an optional technique in case of breath-hold CT acquisition. In our protocol, both PET scans and CT scans were performed with arms elevated. In some PET protocols, the patient scan is performed with arms down along the body; this configuration would create additional deformation in the thorax as compared with CT, which could be possibly corrected by the warping technique. In our study, however, the main reason for the deformation was the position of the diaphragm. More studies would be needed to validate the use of our warping technique in such situations. The linear 9-parameter registration performed reasonably well in cases without large respiratory mismatch, which presumably would be the case when PET scans are to be registered to simulator CT data for radiation therapy planning, or if a fast low-dose, normal breathing CT would be performed in addition to the diagnostic CT for fusion purposes.

An alternative to the nonlinear image registration approach is to perform multiple iterative warps by iteratively maximizing MI because our results indicate it increases after a correct warp. This approach, however, would require a massive amount of computing time because the number of warping parameters in our technique is very large (hundreds) in comparison with a 9-parameter search for the linear transformation. Others attempted to maximize measures of MI with a smaller amount of nonlinear parameters (12), but this number would not allow the smooth local deformations needed in this application. At the same time, we wanted to ensure that warping with such large number of parameters does not introduce spurious local deformations due to the noise in the data; therefore, we smoothed the warp vectors, using local median filtering.

The novel use of combined emission and transmission datasets allows a high degree of initial convergence and full automation of the algorithm. However, the final warping transformation is based on the transmission data alone, ensuring the independence of the functional uptake of the radiopharmaceutical. Including functional emission image in the warp determination could lead to errors, for example, if a part of a lesion visualized on a CT scan is necrotic and does not exactly match the CT anatomic volume.

This study has been applied to thoracic PET/CT scans, in which the full lung coverage was present on both transmission and CT scans; alternative strategies have to be designed for warping of abdominal or head and neck scans because the deformation may be more complex in these areas. In addition, the axial sampling of the CT in this study was 5 mm, which reduces the accuracy of the diaphragm position determination due to possible artifacts in that area. Furthermore, the ray-tracing algorithm to model the lung expansion is to some extent arbitrary and may not truly reflect the mechanical properties of the lungs. Further work in this area is required to establish the best deformation method of the lung that would closely follow the individual respiratory cycles. We also investigated only a subset of possible breathing patterns—namely, breath-hold and a limited number of normal breathing scans. Our approach would need to be validated in other situations, such as imaging during normal expiration or maximum expiration (29). The acquisition of the respiratory gated CT datasets may be required to validate the improvements in the software warping methods.

The principal difficulty in validating the proposed approaches is the lack of a gold standard to determine the algorithm success. Only indirect, “ proxy” measures of the registration can be obtained—for example, the algorithm convergence, reproducibility, and visual assessment. Typically, image registration algorithms have been validated with external fiducial markers in the brain but, in the case of soft tissue and internal organs, this approach is not feasible. We are currently investigating a validation approach that would use the data from the hybrid PET/CT scanner as the gold standard, with PET volumes arbitrarily misaligned using computer software before the re-registration. The validation could then assume the original PET/CT position to be the gold standard. The errors in the intrinsically fused hybrid scanner PET and CT data alignment, however, have been reported to be up to 11 mm in the diaphragm area (30), despite being collected during a single imaging session without apparent patient motion. Therefore, the use of such imperfectly aligned PET/CT data as a reference for the registration algorithm may result in incorrect estimation of the registration errors.

The evaluation of the linear algorithm suggests that the combination of the emission and transmission data, coupled with the multiresolution strategy and MI optimization, is the most effective in this application. Although normalized MI has been suggested as the more optimal technique in brain registration applications (21), we have found that this criterion resulted in less exhaustive search and more failures, when coupled with the simplex minimization algorithm, at least for the type of data tested. The multiresolution strategy allows better convergence and allowed a 95% success rate of the linear component despite of large misalignments (up to 15 pixels); this is due to the fact that initially a more rapid search is performed, allowing more extensive search of the alignment parameters. Use of the multiresolution step reduces the effect of the local-minima entrapment and increases the overall speed of the algorithm and, therefore, it should be always used.

We found that combination of the emission and transmission data results in the best convergence. Most previous approaches have been using exclusively one of the scans (emission or transmission) for the registration. The improved convergence can be most likely attributed to additional information present in both images. For example, spine and kidney structures are well visualized on the emission scans but are not visible on the transmission scans. On the other hand, the external body outlines and lungs are well visualized on the transmission scans. Further improvement of this technique may involve use of the multivariate image registration approach (31) to separate the emission and transmission volumes during the evaluation of the cost function.

The nonlinear image registration is difficult to validate quantitatively without a gold standard. Therefore, we relied primarily on visual verification of the results. One objective measure of the nonlinear alignment is the value of MI after the warp because this measure was not directly used during the warping process. The MI value increased in all cases, indicating that the warping technique applied after linear registration, although based on lung and body surfaces, further improves the statistical dependence of the coregistered volumes. Another quantitative measurement of the warp performance is the comparison of the lung volumes before and after the warp, as performed in this study (Table 4), indicating that lung volumes are similar after warp.

In the light of the recent introduction of PET/CT hybrid scanners (1), the software approach can be viewed from 2 perspectives. On the one hand, it allows automated fusion of PET and CT when only stand-alone PET and CT scanners are available, which can be the case in many departmental configurations. On the other hand, it allows merging of the data irrespective of the time of the acquisition, which is potentially a great benefit for the PET or PET/CT systems for follow-up data comparisons and for the registration with other modalities and additional CT scans. Although the presented method was applied to register and warp transmission data to the CT data, conceivably we could apply a similar technique to the registration of serial CT scans (because the ray tracing was performed on the segmented CT data). In addition, there may be situations when breath-hold CT in the inspiration phase is required and then PET/CT data may be acquired with a second low-dose CT, which would then need to be coregistered to the high-quality inspiration-phase CT using our approach. A future improvement of the registration could be accomplished by the respiratory gated PET coregistered to the inspiration CT (32). Similar registration techniques have been suggested for CT/MRI registration (33) and, therefore, it is likely that such an approach could be used for the registration of PET images to MRI and other modalities.

The automatic PET/CT image registration has several clinical applications. As reported in PET/CT studies, the use of image fusion changed the disease management in 20%–30% of cancer patients (34,35). Coregistered data can also be used in radiation treatment planning applications. Recent reports suggest that planning of radiation therapy is significantly modified when coregistered data are used (36). Further applications of coregistered PET/CT imaging can be explored, such as CT/PET-guided biopsy or image-guided surgery.

CONCLUSION

We have developed a practical and fully automatic algorithm for image registration of thoracic CT and whole-body PET, which includes a nonlinear step for adjustment of normal-breathing PET to inspiration CT. This technique may be applied for automatic fusion of PET and CT acquired at different times on stand-alone scanners.