Abstract
The contribution to red marrow absorbed dose from β-emitting radionuclides distributed uniformly in the total body can be overestimated using either MIRD 11 or MIRDOSE3. The S value assigned to the red marrow target region from activity distributed in the remainder of the body is of particular concern. The assumption that the specific absorbed fraction for total body irradiating red marrow and other skeletal tissues is the inverse of the total-body mass can result in an inappropriate remainder-of-body contribution to marrow dose. We evaluated differences in the calculation of marrow dose using MIRD 11 and MIRDOSE3 formulations and developed methods to correct the results from either to remove inappropriate contributions. When bone takes up significantly less activity than is predicted from an apportionment of remainder-tissue activity based on mass, the standard remainder-of-body correction may substantially overestimate the electron component of the S value from remainder tissues to red marrow using either MIRD 11 or MIRDOSE3. If bone takes up activity, this contribution is negligible using MIRD 11 S values but remains with MIRDOSE3 S values. This overestimate can be significant, particularly when the residence time of activity in the remainder of the body is much higher than in the red marrow and a different correction is needed. As the ratio of the remainder of body to marrow residence time is lowered, the overestimate becomes less significant. Conclusion: In this article, we show the magnitude of this overestimate (which is most important for nuclides with large “nonpenetrating” emission components and for pharmaceuticals that have a large ratio of remainder of body to marrow residence times), show the appropriate corrections to be made in each case, and propose a new method for calculating marrow dose contributions that will avoid this complication in future applications. Because all models give approximate doses for real patients, with uncertainties within those involved in these corrections, we do not suggest that changes be made to existing marrow dose estimates. We suggest only that future calculations be as accurate as possible.
Absorbed dose calculations for radiopharmaceuticals are generally performed using the MIRD technique (1), in which the absorbed dose D to a target organ (rk) is given as:
Eq. 1
where Ãh is the cumulated activity in source region rh (which is a measure of the number of disintegrations that have occurred there), and S(rk ← rh) is the so-called S value, which gives the dose in region rk per unit cumulated activity (per disintegration) in source region rh. Tabulated values of S have been given for many pairs of organs, for 117 radionuclides, using the anthropomorphic model used in MIRD 11 (2). Although not formally published, S values for more radionuclides and phantoms were made available in the MIRDOSE personal computer software (3). In a given problem, one typically has values of cumulated activity for various source regions, such as the liver and kidneys, and a value that represents cumulated activity in the remainder of the body, that is, the total body minus the organs in which a significant concentration of activity was observed. Although not necessitated by the underlying principles of Equation 1, S values typically have been calculated assuming uniform distributions of activity within source regions, with dose averaged uniformly over the target regions. The S values sum the dose contributions from so-called penetrating (photon) and nonpenetrating (electron) radiation for a given radionuclide. Most organs are of sufficient volume for the kinetic energy of nonpenetrating radiation to be absorbed locally. In certain special cases, however, cross-fire of nonpenetrating radiation energy can occur between particular source and target regions; one such special case involves the tissues of the skeleton.
For nonpenetrating radiation, both MIRD 11 and MIRDOSE3 assume that, for all organs, including the red marrow and other skeletal targets, the specific absorbed fraction for total body (TB) as a source is simply:
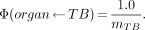Eq. 2
This is because when one calculates the S value for a source in the total body irradiating an organ,
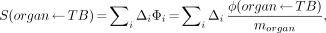Eq. 3
an absorbed fraction for the nonpenetrating emissions of:
Eq. 4
is usually applied, where morgan is the mass of the organ and mTB is the mass of the total body. This fraction derives from two assumptions. First, the fraction (morgan/mTB) of decays that occur in the total body is assumed to occur in the organ (using the traditional rule that activity in the total body is distributed throughout the body, and therefore, the fraction in any organ is the ratio of the organ mass to the total-body mass). Second, all energy emitted in the organ is assumed to be absorbed in the organ (the absorbed fraction for self-irradiation is 1.0). Thus, the S value (for the nonpenetrating component) turns out to be:
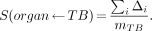Eq. 5
In the case of organs in which cross-fire of nonpenetrating radiation occurs, the assigned absorbed fraction should not be 1.0, and the use of this assumption introduces inaccuracies into the calculation for which compensation must be made.
In the case of bone and marrow, MIRD 11 provides no discussion of this potential problem. One may consult publication ORNL-5000 of the Oak Ridge National Laboratory, Oak Ridge, TN (4), for a sense of the limitation in the dosimetric model underlying the methods, but this potential calculational problem is not discussed there either. The MIRDOSE code attempted to implement the MIRD method and carried over the calculational approach including this potential problem. A direct method to correct for the cross-fire also is not apparent within the MIRDOSE implementation of the bone and marrow model of Eckerman and Stabin (5) (the “Eckerman model”), and, as with MIRD 11, this issue was not discussed in any of the literature supporting the code.
Remainder-of-body (i.e., total body minus source regions) S values, which are obtained by subtracting the source–to–target-region contributions from the total-body–to–target-region S values, must be determined, because these values are not tabulated. These calculations are merely a refinement of the way the basic MIRD absorbed dose equations should be used.
The use of the conventional remainder-of-body S value correction (6), however, can result in an overestimate of the remainder-tissue dose contribution to the red marrow, as will be shown. The reason for this overestimate is that this mathematic correction is needed only for photon emissions, but when it is applied to total S values (including both penetrating and nonpenetrating emissions) using the assumptions of Equations 3 and 4 for organs that have crossfire, explicit compensation must be made for the cross-fire component. This need is not obvious in the remainder-of-body method as described in the literature, and failure to compensate results in incorrect assignment of the remainder-of-body contribution to the total dose. The purpose of this study was to show that the dose contributed from the remainder of the body to the red marrow dose contribution can be overestimated using either MIRD 11 or MIRDOSE3. (Similar arguments would apply to the MIRDOSE2 software, still in use in some sites; however, specific results from this software are not discussed here.) Correction methods for the use of either set of S values will be derived, but more important, a better method for the calculation of total-body S values will be proposed, in which this complication does not occur.
BACKGROUND (OPERATIONAL EQUATIONS)
Consider a pure β-emitting radionuclide of average energy E. MIRD 11 and MIRDOSE3 compute the S value for irradiation of the red marrow (RM) by the hypothetical total body source as:
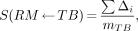Eq. 6
where Δ = k × n × E, n being the abundance of electrons with average energy E, and k being a proportionality constant used to convert units.
In the MIRD 11 and MIRDOSE3 S value tables, the S value for total body irradiating red marrow is calculated using Equation 6. When the standard remainder-of-body (RB) correction (6) is applied:
where S(rk ← RB) is the S value for remainder of body irradiating target region rk, S(rk ← TB) is the S value for total body irradiating target region rk, S(rk ← rh) is the S value for source-region rh irradiating target region rk, mTB is the mass of the total body, mRB is the mass of the remainder of the body (i.e., the mass of total body minus the mass of other source organs used in this problem), and mh is the mass of source-region rh, only specifically identified source regions are included in the summation. The remainder-of- body to red marrow S value, calculated using Equation 7, can be overestimated using either MIRD 11 or MIRDOSE3. The magnitude of this overestimate will depend on whether bone takes up activity.
When bone does not take up activity, additional terms that are not source regions are required in Equation 7 to determine the appropriate dose contribution from the remainder of the body to the red marrow. These terms are the bone components (i.e., trabecular and cortical bone); they should be included in the summation in Equation 7 using MIRD 11, or they should be considered source regions with zero residence times using MIRDOSE3. Otherwise, because of the apportionment of remainder-tissue activity to bone, an unwanted contribution from the remainder of the body to the red marrow will occur using either MIRD 11 or MIRDOSE3, as will be shown shortly.
Equation 7 can lose numeric significance in real problems and loses accuracy when significant cross-fire occurs between source and target regions. The latter problem occurs because correction of Equation 7 was meant only for photon emissions (for which the correction is needed because of the way that total-body specific absorbed fractions and S values are calculated); however, a fortuitous cancellation occurs for nonpenetrating emissions for organs that have no cross-fire component (in Equation 7, both terms involving the nonpenetrating emissions (np) turn out to be ∑ Δnp/mRB, and one cancels the other). If there is cross-fire, however, the terms do not cancel and an error occurs for which a further correction is needed (e.g., for organs with separate wall and content fractions; MIRDOSE3 makes a special correction in this case).
For red marrow, a better approach to the calculation of the S value of Equation 6 is:
Eq. 8
where R is any region of the body and the applicable absorbed fractions are used. (We suggest that the summation exclude the contents of the gastrointestinal tract and urinary bladder, because one cannot assume that their activity concentration is equivalent to that in body tissues.) When the applicable source regions are known, the contribution from the remainder of the body should be computed using Equation 8 rather than the standard procedure used for the remainder-of-body correction (Eq. 7). Again, when bone does not take up activity, the remainder-of-body calculation based on Equation 8 must explicitly subtract the bone components (e.g., trabecular and cortical bone) from the remainder-tissue contribution to the red marrow dose. (Neither MIRD 11 nor MIRDOSE3 considers the yellow marrow as a source region. On the basis of the MIRDOSE3 definition of red marrow, one would expect the yellow marrow to contribute to energy deposition in the red marrow; however, the absorbed fraction φ[RM ← YM], where YM is yellow marrow, has been calculated and found not to contribute significantly in Equation 7.)
An alternative and much simpler solution, which is mathematically equivalent to the use of Equation 8, is not to use the remainder of the body at all to calculate electron doses to any organs. The S value correction, outlined originally in the paper of Cloutier et al. (7) and refined by Coffey and Watson (6), is needed only for photon contributions. Values of Φ(organs ← TB) (with photon and electron emissions combined) are tabulated (e.g., in the MIRD Pamphlet No. 5, Revised (8) and in the Cristy and Eckerman (9) phantom series results), and a correction is needed to avoid double-counting of photon emissions from individual organs considered in a given problem. However, one can calculate S values with the photon and electron components calculated separately. For electrons, one need only assign some fraction of the remainder-of-body activity to the appropriate organs, calculate the β contribution to each organ’s dose, and avoid making the remainder-of-body correction to the electron component of the S value. For photons, one must use the tabulated specific absorbed fractions for the total body and perform the remainder-of-body correction. After separate calculation of all photon and electron contributions to an organ dose, they can be added together to give the total dose to each organ. This calculation method is probably the easiest and safest.
CALCULATIONS (Magnitude of the Overestimate)
The degree to which the remainder-of-body contribution to the red marrow absorbed dose is overestimated will depend on the assigned residence times in the red marrow and total (or remainder of) body. These vary considerably from problem to problem. Residence times in red marrow for monoclonal antibodies, for example, are often assigned on the basis of calculated residence times in blood (10). We compared the MIRD 11 and MIRDOSE3 models using a small residence time of 0.2 h in red marrow and a residence time of 30 h in the remainder of the body. This ratio of residence times is extreme, but the situation can arise in, for example, the use of pretargeting techniques, in which a clearing agent is used to lower the residence time of radioactivity in the blood but the residence time in the total body remains relatively high. The nuclide is 90Y.
MIRD 11.
Thus, S(RM ← RB) = 9.74 × 10−6 rad/μCi h.
The total dose to the red marrow is 0.172 + 0.292 = 0.464 rad/mCi, of which 63% is contributed by the remainder of the body. If bone were to take up no activity, the calculation would stop here and an inappropriate remainder-of-body contribution would be left in the calculation because the MIRD literature gives no guidance on possible corrections. However, one can subtract the bone components, assigning a fraction of the remainder-of-body activity as follows (if bone uptake had been present, these organs would have been included in the summation of Eq. 7). Subtracting the trabecular bone contribution from the remainder term,
Thus, S(RM ← RB) = 1.43 × 10−6 rad/μCi h.
The total dose to the red marrow is 0.172 + 0.043 = 0.215 rad/mCi, of which 20% is contributed by the remainder of the body. Subtracting the cortical bone contribution from the remainder term,
Thus, S(RM ← RB) = −5.6 × 10−7 rad/μCi h.
Because a negative contribution is not possible, this contribution should be set to zero, giving a total dose of 0.172 rad/mCi to the red marrow, all from red marrow. Almost all of the negative dose contribution (approximately −10% error) is caused by rounding (the loss of numeric significance referred to above) in the tabulated MIRD 11 total body to red marrow S value.
MIRDOSE3.
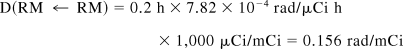
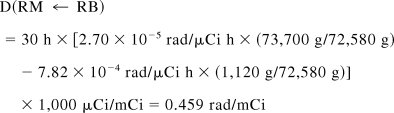Thus, S(RM ← RB) = 1.53 × 10−5 rad/μCi h.
The total dose to the red marrow is 0.156 + 0.459 = 0.615 rad/mCi, of which 75% is contributed by the remainder of the body, compared with the 63% contribution given by MIRD 11. Subtracting trabecular bone from the remainder term,
Thus, S(RM ← RB) = 8.4 × 10−6 rad/μCi h.
The total dose to the red marrow is 0.156 + 0.25 = 0.406 rad/mCi, of which 62% is contributed by the remainder of the body. The S value for cortical bone to red marrow is small, S(RM ← CB) = 7.73 × 10−11 rad/μCi h, and thus makes a negligible contribution. The contribution from yellow marrow is also small. Thus, in MIRDOSE3, even when the bone components are subtracted, the use of Equation 6 results in a remainder-of-body contribution that has no credible origin. In the bone and marrow dose model used in MIRDOSE3 (the Eckerman model), energy originating in the marrow spaces is dissipated in the marrow spaces (which contain a mixture of red and yellow marrow), in the dividing cells on the surfaces of the trabeculae, and within the volume of trabecular bone mineral. Because the S values for trabecular and cortical bone as targets are scoring doses only in a small layer of cells on bone surfaces, the use of the MIRDOSE3 bone model with Equation 6 will not adequately account for the total distribution of energy within the skeletal regions, and thus an inappropriate remainder-of-body dose contribution to the red marrow will remain. Appropriate application of Equation 8, however, will result in a correct calculation of the dose. As noted in the Appendix, “reciprocity” is not expected to exist in the skeleton, because it is a mixture of materials of different densities and atomic compositions. Thus, the fact that the type of correction shown here removed the unwanted contributions (within 10%) with MIRD 11 S values was probably caused by some sort of force fitting of the S values by the MIRD 11 authors. The different definition for source and target organs and the absence of such a fitting approach in the Eckerman model cause this contribution to remain in the MIRDOSE3 calculation.
SOLUTION (REMOVAL OF THE OVERESTIMATE)
Table 1 compares the results of a red marrow dose calculation using the various models and methodologies. The first three rows in the table represent the situation in which bone does not take up activity, and the last three rows represent the situation in which bone does take up activity (or in which bone contributions have been subtracted even though bone did not take up activity). The use of Equation 8 eliminates the extraneous remainder-of-body dose contribution to the red marrow in the case of bone uptake calculated by MIRDOSE3. The difference in the results from use of Equation 6 by MIRD 11 and MIRDOSE3 is explained in more detail in the Appendix.
Results of Three Methods to Determine Red Marrow Dose
If we continue to use 90Y and a remainder-of-body residence time of 30 h but change the red marrow residence time to 2 h, the remainder-of-body contribution (assuming bone uptake of activity) for MIRD 11 drops to 15% and that for MIRDOSE3 drops to 23%. If the red marrow residence time is 5 h, the contributions are 6% and 11%, respectively. Obviously, as the ratio of the remainder-of-body residence time to the red marrow residence time is reduced, the remainder-of-body contribution to the absorbed dose will be reduced accordingly. If one is working with a photon emitter, for which red marrow dose has both a photon and an electron component and for which other organs involved may contribute significantly to red marrow dose, these contributions will be still less important.
DISCUSSION
The issue of an overestimate of the remainder-of-body contribution to the red marrow absorbed dose must be kept in perspective. One should remember that we are still calculating dose to a model, not to a patient. For low doses (diagnostic pharmaceuticals, exposure to occupational radionuclides), the overestimate will be low because of the importance of the photon emissions. In applications to large populations, individual differences will result in uncertainties far greater than any model-based inaccuracies or approximations. For higher doses, particularly in radiotherapy with internal emitters, we know that patient differences from the standard models (patient size, marrow reserve, sensitivity of marrow to radiation because of prior chemotherapy, etc.) cause problems in interpreting observed responses to radiation, and changes on the order of 10%–50% in the model-reported doses are not the problem. Only better, more patient-specific models for marrow dose will result in more accurate dose estimates and better correlations of calculated dose with observed effects. Nonetheless, this calculational problem, now identified, should be corrected so that the applicability of models can be improved without the need to correct for this unwanted contribution.
The correction to new calculations using existing models is most important when absorbed doses to individual patients are important, such as for the therapeutic administration of radiopharmaceuticals. When using MIRD 11, one can calculate the appropriate dose to red marrow using Equation 6 by explicitly subtracting the bone contributions (if bone is not a source organ). Users of MIRDOSE3 can easily correct for unwanted contributions of pure β-emitters by inspecting the output tables that give the percentage contributions from the source organs and removing the remainder-of-body contribution to the red marrow dose (e.g., if this contribution is 30%, the reported red marrow dose should be reduced by a factor of 0.7). If one has a mixed photon–electron emitter, the situation is not as clear-cut; some of the remainder-of-body contribution is appropriate, coming from photons emitted in tissues outside the marrow. In that case, if the correction is needed, the electron component for the remainder of the body to the red marrow will need to be calculated by hand and subtracted from the program-supplied red marrow dose. In future versions of computer codes for internal dose assessment, the use of Equation 8, or the simpler method of summing electron and photon contributions separately, is recommended.
Thus, we reach the following conclusions. First, using standard calculational methods prescribed in the MIRD method and the standard remainder-of-body S value correction, in a situation with marrow and remainder-of-body activity, if no bone uptake is present an overestimate will occur for the dose contribution of the remainder of the body to the red marrow for electrons because of apportionment of remainder-tissue activity to bone, using either MIRD 11 or MIRDOSE3.
Second, when the remainder-of-body correction includes subtraction of the bone components (as would be normal when bone uptake is present or if explicitly done when no bone uptake is present), the use of Equation 6 and the S values of MIRD 11 will result in a negligible remainder-of-body contribution, whereas an inappropriate remainder-of-body contribution will still remain using MIRDOSE3 S values. Use of Equation 8 with the MIRDOSE3 S values will eliminate this inappropriate remainder-of-body contribution.
Third, the magnitude of the remainder-of-body contribution to the marrow dose, and the magnitude of this overestimate, in any case, depend on the relative values (ratios) of the remainder-of-body and red marrow residence times. Typically, the error will be on the order of 10%, but in cases with very large ratios of remainder-of-body to red marrow residence time with electron emitters, the error can be substantial.
Fourth, future applications should avoid these three problems, if possible, through an application of Equation 8 or a better calculational method in which photon and electron dose contributions are maintained separately, the remainder-of-body correction is applied only to the photon contributions, and the total dose contribution is calculated by adding the two components.
CONCLUSION
We have shown that the contribution to red marrow absorbed dose from β-emitting radionuclides distributed uniformly in the total body can be overestimated using traditional MIRD methods, as implemented in both MIRD 11 and MIRDOSE3. The S value assigned to the red marrow target region from activity distributed in the remainder of the body is of particular concern. We have shown differences in the calculation of red marrow dose using MIRD 11 and MIRDOSE3 formulations and have developed methods to correct the results from either to remove inappropriate contributions. We have shown the magnitude of this overestimate and the appropriate corrections to be made in each case, and we have proposed a new method for calculation of marrow dose contributions that will avoid this complication in future applications.
APPENDIX
This appendix provides a more detailed discussion of the remainder-of-body contribution to the red marrow dose and explains the differences between MIRD 11 and MIRDOSE3.
Because of their limited range, only β particles emitted within the red marrow, the marrow space of trabecular and cortical bone, and the mineral bone forming the cavities (trabeculae) will deposit energy within the red marrow (neglecting minor contributions from bremsstrahlung and cortical bone). There is no a priori reason that the sum of contributions from these regions would support Equation 6. However, when one adds up the contributions as tabulated in MIRD 11, they indeed preserve Equation 6, whereas the contributions from MIRDOSE3 do not. MIRD 11 does not discuss this computation; however, ORNL-5000 indicates that the contribution of some components, for example, S(RM ← RM), was based on the assumption that the specific absorbed fraction in skeletal tissues is the inverse of the total body mass. We suggest that this force fitting of the S values to preserve Equation 6 leads one to conclude that a reciprocity relationship (2) exists among the regions. However, because the skeleton is not a “uniform isotropic medium,” the appearance of reciprocity is likely only a consequence of that model and this force fitting.
A difference exists in the contribution to the red marrow absorbed dose from nonpenetrating emitters contained in remainder tissues obtained using MIRD 11 versus MIRDOSE3 S values. This Appendix explains the origin of the inappropriate dose contribution from the remainder of the body to the red marrow and why the contribution approximately cancels using MIRD 11 S values, if bone components are considered, but does not using MIRDOSE3. The use of Equation 8 is necessary to remove this contribution when using MIRDOSE3.
Using Equations 6 and 7 in a problem involving bone uptake, we have:
where TrB represents trabecular bone and CB represents cortical bone.
If the skeleton has approximately reciprocal behavior between bone and marrow,
and we can write:
The sum inside the parentheses in the right-hand term will add to 1, and S(RM ← RB) will go to approximately 0. Obviously, if the bone components are not considered, this sum cannot add up to 1, and this fact is the origin of the overestimates from both MIRD 11 and MIRDOSE3 with no corrections. Then, if reciprocity does not exist, the approximate equalities regarding reciprocity (Eq. 3A) will not hold, and this sum will not add up to one.
Assuming that this approximate reciprocal behavior exists, one can calculate the sum of the absorbed fractions in Equation 4A. The sum of the contributions for nonpenetrating emitters as tabulated in MIRD 11 appear to preserve Equation 6. If this same procedure is applied to the values from the Eckerman model, the bone to red marrow specific absorbed fractions do not appear to display reciprocal behavior because they do not sum to unity. The results of summing the absorbed fractions leaving red marrow are shown in Table 1A. In this calculation, all the sums of absorbed fractions for MIRD 11 were equal to 1.0, within 2%. However, in the text, using S values in a particular problem, an error of approximately 10% was observed. However, for the Eckerman model for 90Y, the sum is clearly different from 1.0.
Sum of Absorbed Fractions Leaving Red Marrow
The fact that the Eckerman model values do not sum to unity does not indicate a problem with this model but, rather, that reciprocity does not hold. In this model, all energy released in the marrow space will not be accounted for by summing the absorbed fractions under the assumption of reciprocal behavior of the specific absorbed fractions. First, one does not expect that reciprocity should hold in the skeleton, because the skeleton is not a uniform isotropic medium. The MIRD 11 model was most likely force-fit to maintain reciprocity between bone and marrow elements. Second, in the Eckerman model, electron energy originating in marrow will be dissipated in marrow, bone surfaces (the 10-μm layer of soft tissue surrounding the marrow cavities), and bone mineral. The value S(RM ← TrB) scores energy in marrow originating from a surface source inside the marrow cavities, whereas S(TrB ← RM) scores energy originating in the marrow and deposited in the 10-μm layer of soft tissue surrounding marrow cavities on the surfaces of trabecular bone, not in the entire mass of trabecular bone. Thus, even if approximate electronic equilibrium were to exist, considerable energy is dissipated in bone regions for which we are not interested in knowing the dose and for which dose was not scored. The definition of the target TrB was limited to a small volume of tissue, not representing the entire 1,000 g of mineral bone. Therefore, the correction formula should not be expected to work, because the use of the definition in Equation 6 assumed a uniform distribution of both electron emission and absorption in all tissues.
In any event, because both the MIRD 11 and the MIRDOSE3 bone models give similar results when used correctly (i.e., when the inappropriate contributions from the remainder of the body to the red marrow are avoided or corrected for), it is appropriate to assume that both models provide reasonable estimates for red marrow dosimetry.
Footnotes
Received Feb. 8, 2000; revision accepted Nov. 17, 2000.
For correspondence or reprints contact: Michael G. Stabin, PhD, Department of Radiology and Radiological Sciences, Vanderbilt University School of Medicine, 1161 21st Ave. S., Nashville, TN 37232-2675.
In this issue
Jump to section
Related Articles
Cited By...
- Evaluation of Safety and Dosimetry of 177Lu-DOTA-ZOL for Therapy of Bone Metastases
- Individualized Dosimetry of Kidney and Bone Marrow in Patients Undergoing 177Lu-DOTA-Octreotate Treatment
- Prediction of Myelotoxicity Based on Bone Marrow Radiation-Absorbed Dose: Radioimmunotherapy Studies Using 90Y- and 177Lu-Labeled J591 Antibodies Specific for Prostate-Specific Membrane Antigen
- Practical Dosimetry of Peptide Receptor Radionuclide Therapy with 90Y-Labeled Somatostatin Analogs
- Bone Marrow Dosimetry Using Blood-Based Models for Radiolabeled Antibody Therapy: A Multiinstitutional Comparison
- Bone Marrow Dosimetry and Safety of High 131I Activities Given After Recombinant Human Thyroid-Stimulating Hormone to Treat Metastatic Differentiated Thyroid Cancer
- Red Marrow Radiation Dose Adjustment Using Plasma FLT3-L Cytokine Levels: Improved Correlations Between Hematologic Toxicity and Bone Marrow Dose for Radioimmunotherapy Patients