Visual Abstract
Abstract
The aim of this study was to investigate the accuracy of single-time-point (STP) renal dosimetry imaging using SPECT/CT data, a nonlinear mixed-effects (NLME) model, and a population-based model selection (PBMS) in a large population for 177Lu-labeled prostate-specific membrane antigen therapy. Methods: Biokinetic data (mean ± SD) of [177Lu]Lu-PSMA-617 in kidneys at time points 1 (1.8 ± 0.8 h), 2 (18.7 ± 0.9 h), 3 (42.6 ± 1.0 h), 4 (66.3 ± 0.9 h), and 5 (160.3 ± 24.2 h) after injection were obtained from 63 patients with metastatic castration-resistant prostate cancer using SPECT/CT. Thirteen functions were derived from various parameterizations of 1- to 5-exponential functions. The function’s parameters were fitted in the NLME framework to the all-time-point (ATP) data. The PBMS NLME method was performed using the goodness-of-fit test and Akaike weight to select the best function fitting the data. The best function from ATP fitting was used to calculate the reference time-integrated activity and absorbed doses. In STP dosimetry, the parameters of a particular patient with STP data were fitted simultaneously to the STP data at different time points of that patient with ATP data of all other patients. The parameters from STP fitting were used to calculate the STP time-integrated activity and absorbed doses. Relative deviations (RDs) and root-mean-square errors (RMSEs) were used to analyze the accuracy of the calculated STP absorbed dose compared with the reference absorbed dose obtained from the best-fit ATP function. The performance of STP dosimetry using PBMS NLME modeling was compared with the Hänscheid and Madsen methods. Results: The function 
was selected as the best-fit ATP function, with an Akaike weight of 100%. For STP dosimetry, the STP measurement by SPECT/CT at time point 3 (42.6 ± 1.0 h) showed a relatively low mean RD of −4.4% ± 9.4% and median RD of −0.7%. Time point 3 had the lowest RMSE value compared with those at the other 4 time points. The RMSEs of the absorbed dose RDs for time points 1–5 were 23%, 16%, 10%, 20%, and 53%, respectively. The STP dosimetry using the PBMS NLME method outperformed the Hänscheid and Madsen methods for all investigated time points. Conclusion: Our results show that a single measurement of SPECT/CT at 2 d after injection might be used to calculate accurate kidney-absorbed doses using the NLME method and PBMS.
Molecular radiotherapy targeting the prostate-specific membrane antigen (PSMA) is a promising palliative treatment option in patients with metastatic castration-resistant prostate cancer (1), using the overexpression of the PSMA in prostate cancer cells (2). [177Lu]Lu-PSMA-617 has shown high treatment efficacy and tolerability in both phase II (3–5) and phase III (6) trials. Although [177Lu]Lu-PSMA-617 therapy is generally well tolerated, several organs, such as kidneys, salivary glands, and bone marrow, are considered organs at risk (7). It has been reported that renal and hematopoietic toxicity are the main side effects of [177Lu]Lu-PSMA therapy and peptide receptor radionuclide therapy (8). Furthermore, the established kidney tolerance dose of 23 Gy based on data from external radiation therapy (5) constitutes the main dose-limiting factor for repeated treatment over multiple cycles. Thus, various protocols for kidney protection using amino acids (9) and dosimetry during [177Lu]Lu-PSMA therapy have been developed.
Calculation of the absorbed dose in molecular radiotherapy dosimetry is based on the time-integrated activity (TIA) and the dose factor (10). Estimating individual absorbed doses in molecular radiotherapy is desirable for therapy optimization and kidney protection. However, the individual absorbed dose is often not calculated in routine clinical practice, as it needs repeated imaging to determine the TIA (11,12). This repeated imaging corresponds to a high workload and additional patient burden, requiring several patient visits. Therefore, a method with fewer imaging sessions is highly desirable.
The feasibility of using a reduced number of imaging data per patient for TIA determination has been investigated for [177Lu]Lu-PSMA therapy (13,14), peptide receptor radionuclide therapy (15–24), radioiodine therapy (25,26), and radioimmunotherapy (27). One of the favorable approaches for dosimetry based on single-time-point (STP) imaging data is the nonlinear mixed-effects (NLME) method (28). For STP dosimetry, it has been shown (17) that the application of NLME modeling resulted in a low number of TIAs with an error exceeding 10% compared with the all-time-point (ATP) TIAs. The percentage of TIAs with a 10% error was approximately 3 times lower than that using the dose mapping methods introduced by Hänscheid et al. (18) and the curve-fitting methods introduced by Madsen et al. (23). Recently, the implementation of NLME and a physiologically based pharmacokinetic model in STP dosimetry could lead to an accurate determination of TIAs in various organs, including kidneys and tumors (11).
Although NLME modeling in STP dosimetry has shown promising results, it has thus far been implemented only in populations with relatively few patients (i.e., 10 (17) or fewer (11) patients). Implementation of the technique in larger patient populations is needed to validate the concept and increase the statistical significance of the accuracy of STP dosimetry with NLME modeling. In addition, identifying the optimal fit function through a population-based model selection (PBMS) (29) with large patient populations is highly desirable for increasing reproducibility. Therefore, in this study, we implemented a PBMS method in the NLME framework to identify the best model describing the [177Lu]Lu-PSMA-617 biokinetic data in kidneys and performed STP dosimetry using NLME modeling in a larger population of 63 patients.
MATERIALS AND METHODS
Biokinetic Data
In brief, biokinetic data of [177Lu]Lu-PSMA-617 in kidneys from 63 patients with metastasized castration-resistant prostate cancer in the first treatment cycle were used in this study (8,30). A [177Lu]Lu-PSMA-617 activity with a median of 6 GBq/cycle was administered intravenously to the patients, followed by SPECT/CT imaging measurements (mean ± SD) at time points 1 (1.8 ± 0.8 h), 2 (18.7 ± 0.9 h), 3 (42.6 ± 1.0 h), 4 (66.2 ± 0.9 h), and 5 (160.3 ± 24.2 h) after injection. Acquisitions were performed on a SPECT/CT scanner (BrightView XCT; Philips Healthcare) using a medium-energy general-purpose collimator. An energy window of ±10% around the 208-keV peak was used for the measurements. Cone-beam CT scans with 30 mAs at 120 kV were used for attenuation correction. Scatter was corrected during reconstruction with the vendor implementation of the effective-scatter source estimation method (31). SPECT was reconstructed using the ordered-subsets expectation maximization algorithm without resolution recovery (8). The calibration factor for 177Lu was measured using the National Electrical Manufacturers Association image-quality phantom. The calculated calibration factor for the imaging protocol used was 9.9 ± 0.4 cps/MBq. Kidney segmentation and analysis were done using the software package Rover ABX (ABX Advanced Biochemical Compounds GmbH) (32). The kidneys were delineated on CT images. At each time point, the activity was measured in both the left and the right kidneys. To compensate for spill-out effects caused by the limited resolution of the SPECT system, all segmented kidney volumes of interest were extended by 2 SPECT voxels in all directions. The enlargement factor was determined by a phantom study. Finally, the fraction of injected activity in both kidneys was used in this study. The institutional review board (vote no. 326/18) approved the retrospective study, and all subjects gave written informed consent.
Fit Function Set: Sums-of-Exponential (SOE) Functions
The following SOE functions were used to describe the biokinetics of [177Lu]Lu-PSMA-617 in kidneys (Eqs. 1–13).
Eq. 1
Eq. 2
Eq. 3
Eq. 4
Eq. 5
Eq. 6
Eq. 7
Eq. 8
Eq. 9
Eq. 10
Eq. 11
Eq. 12
Eq. 13where 
is a fit function, with
being the total number of estimated parameters; 
are the coefficients of the respective exponential terms; 
are the biologic clearance or uptake rates of the radiopharmaceutical in the kidneys;
is the rate of blood circulation set to 
; and 
is the physical decay constant of 177Lu (
, with the 177Lu half-life of 6.6443 d (33)). The 
and 
parameters were constrained to have values greater than 0.
Prior knowledge of radiopharmaceutical kinetics was used as the foundation of the chosen functions and constraints in this study, as suggested by Burnham et al. (34). Therefore, the following were implemented: only SOE functions were considered (35,36); a constraint of 
was used, except for 
and 
; a rapid increase in activity in the kidneys with a half-life of 1 min (ln(2)/
) was added, which is caused by the blood circulation time in humans (29,37); and the radioactive decay was considered as an exponential factor (38–40). The functions 
and 
were added for comparison, as these mono- and biexponential functions, respectively, are often used in the literature (18,23,35).
Study Workflow
Figure 1 shows the workflow of the study. The parameters of the SOE functions (Eqs. 1–13) were fitted to the ATP biokinetic data of [177Lu]Lu-PSMA-617 in kidneys (Biokinetic Data section) using the NLME method (Supplemental Eqs. 1–3) (41,42). In this study, parameters of the SOE functions in Equations 1–13 were modeled as a combination of fixed and random effects. NLME model fittings and simulations were performed in MATLAB software, version R2020a (https://www.mathworks.com/help/stats/nlmefitsa.html). The PBMS NLME approach was used to select the best-fit SOE function describing the data (43). The fittings were randomly repeated 1,000 times to find the best-fit starting values. The SOE function passing the goodness-of-fit test (Supplemental Eqs. 4–6) (35,44,45,47) with the highest Akaike weight was selected as the fit function most supported by the data (35,43,48).
Workflow of study. PBMS NLME approach was used to select best fit function based on goodness of fit and Akaike weight. Reference absorbed doses were based on ATP fittings using best-fit function. STP absorbed doses were calculated analogously using only STP data for investigated patient. RDs and RMSEs were used to analyze accuracy of STP absorbed doses against reference absorbed doses. AICc = corrected Akaike information criterion; i = time point; N = total number of patients; NLMEM = PBMS NLME; rAD = reference absorbed dose; rTIA = reference TIA; sAD = STP absorbed dose; sTIA = STP TIA.
The best-fit SOE function from the model selection and ATP fitting was then used to calculate the reference TIA (Fig. 1). Calculation of the TIAs was based on the analytic solution of the SOE functions. In STP dosimetry, the parameters of a specific patient with STP data were fitted simultaneously to the STP data at different time points of that patient with all data points of all other patients.
The STP dosimetry methods introduced by Hänscheid et al. and Madsen et al., which have been widely adopted in STP studies (20,22,49–51), were implemented in this study for comparison. The methods were initially used to describe the biokinetics of [177Lu]Lu-DOTATATE/TOC and [90Y]Y-DOTATOC (18,23). In this study, the methods were assumed to be applicable for [177Lu]Lu-PSMA-617. The corresponding TIAs for the Hänscheid and Madsen methods were calculated using the following equations:
Eq. 14
Eq. 15where 
is the activity measured at time point i, 
is the time of measurement i, and 
is the population effective clearance rate constant calculated using the leave-one-out method.
The S value of 2.93 × 10−5 Gy × min−1 × MBq−1 (46,52) for male patients was used to calculate the absorbed dose using NLME ATP fitting (reference absorbed doses), NLME STP fitting (STP absorbed doses), and the STP Hänscheid and Madsen methods.
Relative deviations (RDs) and root-mean-square errors (RMSEs) were used to analyze the accuracy of the calculated STP absorbed doses, STP Hänscheid method, and STP Madsen method with the reference absorbed doses as the reference. The RDs and the RMSEs were calculated according to
Eq. 16
Eq. 17where sAD is STP absorbed dose, rAD is reference absorbed dose, 
is the RD of the STP method at time point k, 
is the root-mean square of 
over all patients, and 
is the SD of 
. The reference TIA was computed through population fitting, using a notably high parameter-to-data ratio within our dataset, specifically 315 data points and 13 parameters (Table 1). In contrast, individual patient fitting using a monoexponential function as in the Hänscheid and Madsen methods uses a significantly lower ratio, such as 3 data points and 2 parameters. This results in a higher uncertainty of the resulting TIA.
PBMS with NLME Model Results for ATP fitting
RESULTS
The NLME fittings for functions f4b, f5a, 
, 
,
, 
, 
, and 
did not pass the goodness-of-fit test. On the basis of the PBMS NLME method, the function 
was selected as the best-fit function, with an Akaike weight of 100% (Table 1; Supplemental Fig. 1; supplemental materials are available at http://jnm.snmjournals.org). The estimated fixed-effect values are presented in Table 2. The estimated random-effect values ranged from 0.08 to 0.52. The intraindividual variability (a in Supplemental Eq. 3) was 0.079. Figure 2 shows the percentage RD of the TIAs from ATP fitting with functions f2, f3, f4a, and f4c to the TIAs from ATP fitting with function f6a. The mean percentage RDs in Figure 2 are 1.3% ± 14.4%, 1.1% ± 14.2%, 0.1% ± 1.9%, and 0.2% ± 2.0% for functions f2, f3, f4a, and f4c, respectively.
Parameters Estimated from ATP Fitting Obtained from Best Function Derived Using PBMS with NLME Modeling (i.e., 
)
RD values of TIAs obtained from ATP fitting using functions f2, f3, f4a, and f4c to TIAs obtained from ATP fitting using best function according to PBMS NLME method, that is, f6a. Box plots show median, 25th and 75th percentiles, whiskers at 5th and 95th percentiles, and outliers. Percentage RDs for functions f4a or f4c are relatively small because of marginal contribution of uptake phase. Function f3 was added for comparison in Figure 2, as this function is often used in the literature (17,35,39). For broad range of covered sampling times after injection in population investigated here, single biologic elimination phase (as is also case for f2) is insufficient.
Figure 3 shows the population RD of the absorbed dose for STP dosimetry at different time points. The mean of the population RD for STP dosimetry is shown in Supplemental Table 1. The medians of the population RD for STP dosimetry at time points 1–5 were −2% (range, −55% to 59%), −4% (range, −53% to 10%), −0.7% (range, −39% to 20%), −0.1% (range, −32% to 106%), and 0.4% (range, −40% to 348%), respectively. The RMSE values of the absorbed dose RDs for time points 1–5 were 23%, 16%, 10%, 20%, and 53%, respectively. Thus, the STP dosimetry at time point 3 has the lowest mean RD and RMSE values.
RD values of TIAs obtained using PBMS NLME (NLMEM) function 
(Eq. 8), Hänscheid method (Eq. 14), and Madsen method (Eq. 15) for STP dosimetry at time points 1–5. TIAs from ATP fittings calculated using PBMS NLME function f6a were used as reference values. Box plots show median, 25th and 75th percentiles, whiskers at 2.5th and 97.5th percentiles, and outliers. TP = time point.
Use of STP dosimetry with the PBMS NLME method outperformed the Hänscheid and Madsen methods for all time points (Fig. 3; Supplemental Table 1). The STP NLME model at time point 3 could not accurately calculate the TIA in a few outlier patients (outside the mean ± 2 SDs of the RD), that is, patients 12, 36, 41, and 44, with absorbed dose RDs of 26%, 39%, 23% and 29%, respectively (Fig. 4).
Time–activity curves from ATP (green lines) and STP (black lines) fittings at time point 3 simulated with function f6a for 4 outlier patients. Estimated individual parameters indicate that these outliers had lowest biologic clearance 
(4.8 × 10−3/h to 6.7 × 10−3/h) in population and were relatively lower than fixed effect (9.1 × 10−3/h) (Table 2), a well-known behavior in STP dosimetry (17). P = patient.
DISCUSSION
In this study, 315 biokinetic data were used and the SOE function 
was selected from the PBMS NLME method based on the goodness-of-fit test and Akaike weight of 100% (Table 1). The SOE function 
shows 2 uptake and clearance phases of the radiopharmaceutical in kidneys. This function shows a higher parameter-to-data ratio in our patient population than the frequently used monoexponential function in the literature (Fig. 2) (18,23). The total number of exponential terms and parameters in this study for [177Lu]Lu-PSMA-617 (4 exponentials and 6 parameters) is higher than found in our recent study for [177Lu]Lu-PSMA-I&T (
[2 exponentials and 3 parameters]) (43). These differences can be attributed to the total number of data and the schedule and range of the measurements between the studies, that is, 315 biokinetic data of [177Lu]Lu-PSMA-617 measured between 0.7 h after injection and 236 h after injection (this study) versus 46 biokinetic data of [177Lu]Lu-PSMA-I&T measured between 0.5 h after injection and 168 h after injection (43). This shows that adding more data covering a broader time range is beneficial as it allows the identification of a function with a larger number of parameters. This function should in turn be able to better reflect the biokinetics of the radiopharmaceutical.
It has been shown that STP data at 48 h after injection would lead to a relatively accurate prediction of kidney TIAs for [177Lu]Lu-PSMA (20). For [177Lu]Lu-PSMA-I&T therapy, simulation results by Rinscheid et al. showed STP data at around 52 h after injection as the optimal time point for calculating kidney TIAs (14). This work identified time points 2 and 3, having a relatively low mean and median RD of absorbed doses (Fig. 3) in our [177Lu]Lu-PSMA-617 dataset. Time point 3 (42.6 ± 1.0 h) was identified as having the lowest RMSE value. Time point 3 in our study for kidneys is consistent with the optimal time point for STP dosimetry reported in the literature (14,20).
The percentages of the total number of patients with absolute RDs higher than 10% for STP dosimetry using time points 1–5 were 59% (n = 37), 40% (n = 25), 24% (n = 15), 35% (n = 22), and 38% (n = 24), respectively (Supplemental Table 1). Time point 3 was selected as optimal for STP dosimetry as it has the lowest RMSE and mean RD value. Therefore, PBMS NLME and STP imaging of [177Lu]Lu-PSMA-617 kinetics might be used to determine absorbed doses in kidneys accurately, with only 4 outliers (RDs outside the threshold of mean ± 2 SDs) at time point 3 (Fig. 4).
The fractions of percentage RDs lower than 10% for STP dosimetry at time point 3 using the methods of Hänscheid et al. and Madsen et al. were 0.44 and 0.41, respectively, whereas the best model according to the PBMS NLME approach demonstrated that the fraction of percentage RDs lower than 10% for STP dosimetry at time point 3 was 0.76. This finding aligns with the literature, suggesting that NLME modeling can reduce the number of patients with a percentage RD lower than 10% calculated using the Hänscheid and Madsen methods (17). One contributing factor to these results is the use of monoexponential functions (f2) (18,23). The monoexponential function had a lower quality in describing the biokinetic data in our patient population than the best model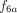 
derived from PBMS NLME (Fig. 2; Supplemental Table 1). The superiority of our method in this study may also be attributed to the different radiopharmaceuticals (including the different functions used) and the different study populations.
In this study, calculation of the absorbed dose was based on the self-dose. The kidney non–self-dose has been reported to contribute up to 10% to the kidney dose for [177Lu]Lu-DOTATATE (53). Therefore, further study is needed to investigate how to add the non–self-dose using STP dosimetry with the PBMS NLME method.
NLME modeling uses a population pharmacokinetic approach, wherein instead of individually fitting the data from each individual, all data within the population are simultaneously fitted. The benefit of using NLME models is that they do not require the data to be comprehensive or densely sampled, as is often the case in nonlinear regression analyses with individual data points (41). Thus, the reference TIA was computed through population fitting, using a notably higher parameter-to-data ratio within our dataset, specifically 315 data points and 13 parameters (Table 1). In contrast, individual patient fitting using a monoexponential function uses a significantly lower ratio, such as 3 data points and 2 parameters. This results in a higher uncertainty of the resulting TIA.
In a clinical context, for a new radiopharmaceutical or a new patient population, the STP method introduced here plays a crucial role in the following sequence of steps. The first step is to collect biokinetic activity data during therapy from the patient population of interest. The second is to determine the most suitable fit function based on the data using the PBMS NLME method presented here. This will yield the corresponding fixed-effect and random-effect parameters (Table 2). The third is to conduct STP dosimetry for new patients by applying NLME modeling, using the identified optimal function along with the fixed-effect and random-effect parameters determined in step 2.
Thus, for a known radiopharmaceutical and patient population, step 3 is sufficient, as once the data are obtained in step 2, these can be used for STP dosimetries in every center. Therefore, our results can be used for other studies if the radiopharmaceutical and patient populations are equivalent and appropriate image quantification is ensured.
A prerequisite of NLME modeling is the need for a historical cohort with multiple-time-point [177Lu]Lu-PSMA-617 SPECT/CT data (step 1). Because of the reimbursement policies, the availability of posttreatment SPECT/CT imaging is increasing (17). Additionally, promoting data exchange among different health care centers, exemplified by the information offered in this publication, can streamline the model development process.
CONCLUSION
In this study, we developed and implemented an STP dosimetry using NLME modeling and PBMS to calculate kidney-absorbed doses of [177Lu]Lu-PSMA-617. Our results show that a single measurement of SPECT/CT at 2 d after injection might be used to calculate accurate kidney-absorbed doses.
KEY POINTS
QUESTION: Can a nonlinear fixed-effects model with PBMS using many biokinetic data covering a broad postinjection time range provide accurate STP-based kidney-absorbed dose estimates for patients treated with [177Lu]Lu-PSMA-617?
PERTINENT FINDINGS: A single measurement of SPECT/CT at 2 d after injection may be used to calculate accurate kidney-absorbed doses using NLME modeling. The mean RD for STP at 2 d was −4% ± 9%, with only 24% of the total number of patients having RDs higher than 10% (15/63 patients) and only 10% of the total number of patients having RDs higher than 20% (6/63 patients).
IMPLICATIONS FOR PATIENT CARE: The STP method presented in this study holds great potential to be integrated into routine clinical practice, thereby increasing the acceptance and use of individualized dosimetry, which will benefit patients by predicting related risks.
DISCLOSURE
This work was supported by a PUTI Q1 grant 2023 from Universitas Indonesia (grant NKB-467/UN2.RST/HKP.05.00/2023). No other potential conflict of interest relevant to this article was reported.
Footnotes
↵* Contributed equally to this work.
Published online Feb. 29, 2024.
- © 2024 by the Society of Nuclear Medicine and Molecular Imaging.
REFERENCES
- Received for publication July 5, 2023.
- Revision received January 23, 2024.
In this issue
Jump to section
Related Articles
Cited By...
- No citing articles found.