Revisiting an Old Issue: The Discrepancy Between Tissue Ratio–Derived Binding Parameters and Kinetic Modeling–Derived Parameters After a Bolus of the Serotonin Transporter Radioligand ¹²³I-ADAM

In vivo neuroreceptor imaging research based on radiolabeled probes has been performed in 2 imaging modalities—PET and SPECT. It is generally agreed that PET is the more quantitatively precise of the two (1) for a variety of reasons, such as the ease with which accurate attenuation correction can be implemented, or the better spatial resolution of PET in commercially produced scanners. Additionally, the fact that there are See page 247positron-emitting isotopes of small atoms, especially ¹¹C, has led to a large number of PET probes with affinity for numerous targets. But the short half-life of ¹¹C is also the source of one of the main limitations of PET:¹¹C-labeled radioligands require onsite cyclotrons and local expertise in radioligand synthesis. This limitation generally restricts brain PET research to large academic institutions capable of supporting these instruments and staff. The longer half-lives of SPECT isotopes make it possible to conduct brain imaging research at institutes that do not have the infrastructural support for research PET, potentially gaining access to clinical populations that may not otherwise be included in imaging research. Thus there is a continued role for SPECT in imaging research, and there are target molecules that are studied with both modalities.

The serotonin reuptake transporter is one such target molecule of great interest in PET and SPECT neuroimaging. Because of its localization on serotonergic nerve terminals, serotonin transporter binding has been interpreted as a marker for the density and integrity of the serotonin system. Imaging studies have been used to investigate serotonin transporter in mood disorders (2,3), obsessive-compulsive disorder (4,5), alcohol dependence (6), and substance abuse (7,8). Early studies were performed using ¹²³I-2β-carbomethoxy-3β-(4-iodophenyl)tropane (¹²³I-β-CIT) (9), the only imaging agent available at the time. But ¹²³I-β-CIT has similar affinity for dopamine transporters and serotonin transporter (10) and so cannot unambiguously image serotonin transporter in regions where both proteins are abundant. This is especially so in the striatum, where serotonin transporter density is high, but dopamine transporter density is an order of magnitude higher; ¹²³I-β-CIT is used to image dopamine transporters in striatum. Eventually, several additional ligands that are much more highly selective for serotonin transporters became available for imaging humans, including trans-1,2,3,5,6,10-β-hexahydro 6-[4-(methylthio)phenyl]pyrrolo-[2,1-a]-isoquinoline (¹¹C-McNeil 5652) (11) and ¹¹C-N,N-dimethyl-2-(2-amino-4-cyanophenylthio)-benzylamine (¹¹C-DASB) (12) for PET and ¹²³I-labeled 2-((2-((dimethylamino)methyl)phenyl)thio)-5-iodophenylamine (¹²³I-ADAM) (13) for SPECT. To date, there are more than 30 published ¹²³I-ADAM studies; at least 12 of these were performed on humans.

The underlying pharmacokinetic theory that has led, over the past 2 decades, to the development of robust models for the extraction of parameter estimates from imaging experiments applies equally to PET and SPECT data. But these modeling approaches have been adapted more wholeheartedly in the PET rather than the SPECT literature, where data analysis frequently consists of measuring concentration ratios between receptor-rich regions and reference regions devoid of receptors during some fixed interval after tracer injection. In particular, several published ¹²³I-ADAM studies on humans have used ratio methods for data analysis. These ratios, however, truly represent the desired parameter (binding potential relative to the nondisplaceable component of the brain signal [BP_ND]) only under steady-state conditions and not when concentrations are changing with time, as is the case after a bolus injection of this radioligand. In this issue of The Journal of Nuclear Medicine, Frokjaer et al. (14) remind us of the foibles of this approach. These authors have acquired ¹²³I-ADAM data for human subjects and have compared several simplified approaches for data analysis—reference region methods (simplified (15) and graphical (16)) and the ratio method—with full kinetic modeling using arterial plasma samples as an input function. They have demonstrated that tissue ratios, taken late in the scan, greatly overestimate BP_ND relative to the plasma-based approach, whereas the other methods do not. This is not a new issue in the brain imaging literature. It was explored in depth by Carson et al. (17) but is a discussion worth repeating.

Intuitively, late in an experiment after a bolus injection of radioligand, the concentration in the reference region will approach its equilibrium value, relative to the low plasma levels of radioligand, more rapidly than will the concentration in a receptor-rich region, because of the comparatively slow rate of dissociation of receptor-bound ligand. This phenomenon has been described in mathematic detail (17); a brief mathematic exposition is given below for a simple special case of practical relevance. This phenomenon would be of little consequence if it led to a uniform bias across subjects—researchers are generally more interested in comparisons across conditions or populations than in the absolute quantification of BP_ND. However, the magnitude of the effect will depend on the peripheral clearance of the radioligand. How far the ratio-based estimate of BP_ND varies from the true value will be a function of the relative distances of the receptor-rich region and reference region concentrations from their equilibrium values relative to the plasma levels at the time of measurement, and these in turn will be functions of the rate at which the radioligand clears from the plasma. Pathologic states or experimental manipulations that are associated with clearance differences between studied groups could potentially lead to measured differences that would be misinterpreted as authentic differences in BP_ND.

In their article, Frokjaer et al. make recommendations on the relative accuracy and robustness of the graphical and simplified reference tissue model approaches; they favor the graphical method. In the future, other authors may test these and perhaps some of the many published variants and refinements (18–21) with ¹²³I-ADAM. They may or may not arrive at the same conclusions; modeling specialists have long debated the fine points of the various techniques and will no doubt continue to do so. But the bigger picture is that all these methods are based on pharmacokinetic models that account for the relationship between arterial plasma concentration and brain concentration and lead to binding parameter estimates that are independent of peripheral clearance, whereas the ratio approach, when applied during conditions other than steady state, does not.

In the following mathematic explanation for a special simple case, assume that concentrations in the receptor-rich region (C_T) and in the reference region (C_R) are well described by a “1-tissue-compartment model”; this is the case for many serotonin transporter ligands, including ¹²³I-ADAM as demonstrated by Frokjaer et al. Then the 2 brain regions satisfy the differential equationsEq. 1where C_P is the plasma concentration, and the delivery constant K₁ is taken as equal across regions for notational and analytic simplicity. The constants k₂ and k_2a are the rate constants for efflux from brain. In general, k_2a is less than k₂; that is, efflux from the receptor-rich region is slower than from the reference region because of dissociation from the receptor pool. At equilibrium, the left side of each equation equals 0, and the concentrations satisfy the relationshipsEq. 2where V_T (total distribution volume) and V_ND (nondisplaceable distribution volume) are the distribution volumes of C_T and C_R. BP_ND, estimated from tissue ratios (measured at equilibrium), is then given by the following (22):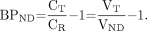Eq. 3When the brain concentrations are not at steady state, however, the left sides of Equation 1 are not zero. In the late, washout, phase of the experiment, both are negatively valued functions of time, because the concentrations are decreasing. In this case, rearrangement of Equation 1 and substitution into Equation 3 leads toEq. 4Because both derivatives are negative, both C_T and C_R will exceed their respective equilibrium values relative to C_P. The magnitude of BP_ND estimated from tissue ratios during this phase, relative to the true BP_ND, will be determined by the relative magnitudes of |dC_T/dt| and |dC_R/dt|. Because C_R will equilibrate with C_P more rapidly than C_T does, eventually |dC_T/dt| is greater than |dC_R/dt|, that is, C_R is “flatter” than C_T late in the scan (Fig. 1 in Frokjaer et al.), and apparent BP_ND will exceed true BP_ND. The particularly straightforward form of Equation 4 follows from the simplifying assumption of equal K₁ across regions, but the same principle applies as well when delivery is not equal across regions, although the exact turning point when estimated BP_ND switches from less than true BP_ND to greater than true BP_ND may be different. Note that even when the ratio C_T/C_R is nearly constant (sometimes called pseudo or secular equilibrium), say C_T = βC_R, for some β > 1, dC_T/dt = βdC_R/dt so that apparent BP_ND still exceeds true BP_ND. This phenomenon is clearly demonstrated in Figure 3 in the Frokjaer et al. report (and is also shown in Fig. 4 of Carson et al (17)).

• Received for publication October 2, 2007.
• Accepted for publication October 22, 2007.