Abstract
Performance tests on lutetium oxyorthosilicate (LSO)–based PET scanners cannot be conducted strictly according to the National Electrical Manufacturers Association (NEMA) NU 2 standards because of the presence of intrinsic radioactivity within the LSO crystal scintillator material. This background radiation gives rise mainly to random coincidence events but also to a small number of true coincidences, which cannot be eliminated from measurements on such scanners and must therefore be corrected for in the data analysis. The current NU 2 standards do not take account of these backgrounds and hence can lead to erroneous results on LSO-based machines. Nevertheless, the intent of the standards can be met with appropriate modifications to the acquisition and processing procedures. In this paper, we propose certain changes to the NEMA specifications to accommodate this class of scanners. These changes affect mainly the estimation of sensitivity, scatter, randoms, and count losses. Using these modified procedures, the NU 2 performance of LSO-based systems can accurately be measured.
- background
- intrinsic radioactivity
- lutetium oxyorthosilicate
- National Electrical Manufacturers Association
- NU 2
- PET
The NU 2-1994 and NU 2-2001 standards published by the National Electrical Manufacturers Association (NEMA) (1,2) are widely used for characterizing the performance of PET scanners (3,4). These documents specify procedures for acquiring and analyzing data using standard phantoms and sources. They also specify criteria that are intended, in part, to ensure that background event rates are negligible during certain of these acquisitions. An example is the limit on random coincidence rate specified for the measurement of scatter fraction in NU 2-2001 (section 4). Although scanners using conventional scintillator detector materials such as bismuth germanate or NaI can generally meet these standards, they may not all be met when the detector material emits significant intrinsic radiation, as is the case with the new lutetium oxyorthosilicate (LSO) scintillator. This intrinsic radiation gives rise to significant background event rates that cannot be eliminated by following the current NU 2 procedures. Thus, not all these standards can be applied directly to LSO-based scanners without error. The purpose of this communication is to propose certain modifications to the NEMA NU 2 standards that properly account for the effects of the intrinsic radiation and permit accurate measurement of the performance of LSO-based scanners. We explicitly discuss the NU 2-2001 standard measurements; analogous adjustments can be developed for the NU 2-1994 measurements.
LSO contains natural lutetium, of which the radioactive nuclide 176Lu composes 2.6%. 176Lu decays by β− emission, followed by a cascade of γ- and x-rays over a broad energy spectrum. The resulting background counting rate depends on the construction of the detector and the energy window used for discrimination. For the LSO block detectors used in the ACCEL dedicated PET and LSO PET/CT scanners (CPS Innovations), the background single-event rate is typically about 7.5 kcps, for an energy window of 350–650 keV. The scanner cannot distinguish between these intrinsic events and events arising from extrinsic sources such as a patient; each contributes in the same way to measured random coincidences. The total block singles rate in clinical scans may range up to 160 kcps or higher. Considering that the random coincidence rate is approximately proportional to the square of the singles rate, one can estimate (considering also dead-time losses) that the presence of the intrinsic singles increases the randoms rate by about 8% at these higher counting rates, compared with what it would be without the background radiation. The relative contribution of the intrinsic randoms is of course greater at lower counting rates. This is illustrated in Figure 1, which shows a plot of the randoms-to-trues ratio (RTR) versus the average block-detector single-event rate for a NEMA NU 2-2001 (section 4) counting-rate test on an ACCEL. The minimum value is 0.17 at a singles rate of 15 kcps per block. In the absence of the intrinsic or other background, the RTR would have fallen monotonically to zero as the activity diminished. Clearly, the NU 2-2001 criterion that the RTR be less than 0.01 in the last frames of this test cannot be met on such scanners. This would have serious consequences for the estimation of scatter from this test, as has been discussed in detail (5).
RTR for a NEMA NU 2-2001 counting-rate test performed on an ACCEL, as a function of the average singles rate in a block detector.
In addition to random coincidences, the intrinsic radiation may also give rise to a small number of true coincidences. An intrinsic true event may result when a 176Lu nuclide undergoes β-decay in one detector, depositing energy locally in that detector, and also emits a prompt γ-ray (isotropically) that is absorbed in a second detector. The total rate of such events for the ACCEL or LSO PET/CT scanner, for an energy window of 350–650 keV, is only about 600 cps in a scan performed with no objects in the field of view (FOV) of the scanner. These events are distributed uniformly across the FOV. The rate may be significantly higher if lower, wider energy windows are used (5). When an object such as a patient is in the scanner, the intrinsic trues are attenuated by the object, similarly to the annihilation radiation. Generally, these events are of no consequence in the clinical scanning regime for the ACCEL or LSO PET/CT scanner, for which total true-event rates may be more than 1,000 times higher than the (attenuated) intrinsic trues contribution. In fact, because of their very low level, current commercial scanners do not make an explicit correction for the intrinsic trues. On the other hand, the effect of intrinsic trues can be significant and should be compensated when scanner sensitivity or scatter fraction is measured using very low activity levels.
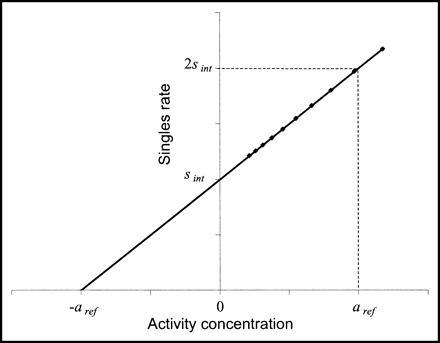
It is useful to define a characteristic extrinsic activity threshold, aref, above which the response of the system is determined more by the radiation originating external to the detectors than by the internal activity. Considering Figure 1, the point at which RTR is minimized seems like a natural choice. Neglecting counting losses, the random coincidence rate is proportional to s2, where s is the total singles rate. Similarly, the true coincidence rate is proportional to (s − sint), where sint is the intrinsic singles rate. From this, it is easy to show that the minimum of the RTR should occur at 2sint. We thus define aref as the external (to the detectors) source activity, or activity concentration when appropriate, at which s = sref = 2sint. This is illustrated in Figure 2, which clearly shows that aref is the intrinsic equivalent external activity, that is, the activity level in the object being scanned that would give rise to the same singles rate as that produced by the intrinsic radiation. For the present example, aref = 0.61 kBq/mL in the 22-L, 70-cm-long phantom, or a total activity of 13.4 MBq, most of which would be outside the FOV of the camera. This activity is approximately 4% of that at which the peak noise equivalent counting rate (NECR) occurs. The reference activity aref is a key concept in our recommendations. The value of aref corresponding to sref will vary from one test to another, depending on the emitter and attenuation distributions in the source. sint can easily be measured by removing all external activity from the vicinity of the scanner and performing a brief acquisition.
A plot of the singles rate trend at low activity, showing the definition of aref.
The NEMA standards specify that certain measurements be performed with RTR < 0.01. Although the minimum RTR depends somewhat on the source configuration, for the NEMA test configurations the randoms rate are not likely to fall below 1% of the trues rate. However, the intent of the NEMA procedures in these cases is not to achieve a low randoms rate per se but, rather, to isolate one physical characteristic of the scanner from another; for example, to measure the intrinsic spatial resolution of the system without the complications of pileup and mispositioning that may occur at higher counting rates, or to measure the scatter component of the true coincidences without contamination from random coincidences. These goals are still achievable on LSO-based machines with appropriate acquisition and analysis techniques.
The NEMA tests for spatial resolution and sensitivity are to be performed at low counting rates to avoid biasing results through inaccurate corrections for dead time, pileup, and randoms. Bias due to randoms correction is not an issue with scanners that use a delayed coincidence window technique for measuring and subtracting random coincidences. Thus, the presence of additional randoms due to the intrinsic radiation will not bias results but may require acquisition of 10%–20% more counts at low activities to achieve an equivalent integral signal-to-noise ratio in the data, compared with non-LSO systems (based on a simple NECR estimate). In fact, the effect of randoms is probably much less for these tests, since the randoms will be distributed more uniformly than are the spatially localized trues.
Another consideration in the case of intrinsic radiation is its contribution to count losses. Several of the NEMA tests require that these be <1%. Dead time in the system will in principle be greater at a given extrinsic source activity with the intrinsic events present, because of competition for processing time and multiplexed data channels. However, experimentally, dead time is defined in terms of the deviation of a response (e.g., trues counting rate vs. source activity) from a linear trend extrapolated from “low-counting-rate data.” Somewhat ambiguously, low-counting-rate data are defined as those having <1% dead time. The intent appears to be to operate in a low-activity regime in which the maximum deviation from linearity is less than 1%. Empirically, we find that this goal can be met for the LSO-based scanners mentioned above over a reasonably broad range of activities in the vicinity of aref. Figure 3 shows total trues versus activity for the NU 2-2001 70-cm phantom on an ACCEL (same data as for Fig. 1). A linear regression to the data from aref = 0.61 kBq/mL down to an activity lower by a factor of 4 (2 half-lives) is also shown. The maximum deviation of these data from this linear trend is <1%. The linearity of the system’s response at singles rates below sref is an important criterion for the definition of aref. If, on some system, the trues counting rate were found not to be linear to within 1% up to sref = 2sint, then the value of sref, and hence aref, for that system should be lowered appropriately. For the purpose of extrapolating a linear trend to higher activities in order to evaluate count losses, we believe a least-squares fit of a linear function in this range is preferable. To ensure adequate statistics, we suggest acquiring 8 frames in the interval from aref to aref/4, each one-quarter half-life long.
Trues rate at low activity from a NEMA NU 2-2001 counting-rate test on an ACCEL. Also shown is a linear trend fitted to the data below 0.61 kBq/mL.
The modifications to the standards proposed here have served as the basis for the measurement of the complete NEMA test suite for an LSO PET/CT scanner that is presented in an accompanying article in this issue (6). The NU 2-2001 corrections accuracy (section 6) and image quality tests (section 7) require no special implementation on LSO-based scanners, although if a correction for intrinsic trues is available it may be applied for these reconstructions.
RECOMMENDATIONS
Spatial Resolution
For this measurement, NU 2-2001 specifies that both the dead time and the ratio of random to total events be <5%. The physics issues are that spatial pileup and background in the data should be low enough not to influence the estimate of the widths of the point sources in the reconstructed images. We believe these criteria can be met if the total activity of all the sources simultaneously in the FOV is <2aref. This belief is based on the counting-rate data of Figure 3, which shows that counting losses are significantly less than 5% at this point. On the other hand, extremely low activities (<0.1 aref) should be avoided since the background from intrinsic trues could eventually become significant. aref here may be considerably less than for the counting-rate test, since the point sources are fully contained in the FOV and are not appreciably attenuated. aref is typically a few megabecquerels. The data should be corrected for randoms using the delayed coincidence window technique. To ensure the quality of the data after randoms subtraction, we suggest acquiring 20% more counts during the test than the quantity specified by NEMA. If a correction for intrinsic trues is available during reconstruction of the data, the correction may be applied, although the relative contribution of the trues is expected to be quite small.
Scatter Fraction, Count Losses, and Randoms Measurement
The NEMA NU 2-2001 procedure (section 4) specifies that the counting-rate analysis be performed on prompt coincidence data (trues plus scatter and randoms) only, under the assumption that low-activity frames contain negligible randoms. Application of this prescription to LSO detector data, however, would significantly overestimate the scatter fraction (5) and very inaccurately estimate the randoms. A more exact approach is to measure the counting rates in both prompt and delayed coincidence windows. From these data, the randoms and scatter can be estimated accurately. In addition, the scatter fraction can be determined as a function of counting rate. The current NEMA standard neglects the counting-rate dependence of the scatter fraction.
Data Acquisition.
Both the prompts and the delayed sinograms should be acquired. The NEMA stopping criteria are that trues losses and randoms both be less than 1% of trues. The second of these is not achievable. Instead, we recommend scanning until the activity in the phantom is reduced to aref/4. On a current-generation ACCEL, for instance, this implies a stopping activity of approximately 0.15 kBq/mL (0.004 μCi/mL), or approximately 1% of the peak NECR activity. If the line source is initially loaded with 740 MBq (20 mCi) 18F, then data must be acquired for 14.3 h. To measure the intrinsic trues also, a final acquisition should be made with the source removed from the phantom and gantry but with the polyethylene cylinder still in place.
Trues and Totals.
True-event-rate estimation should follow the standard NEMA prescription, applied to the prompts sinogram. After trimming the sinogram to a 12-cm radius and aligning the peak values of each projection, trues are the integral of the counts above a linearly interpolated background within a 2-cm radius. Totals are the sum over all counts in the trimmed prompts sinograms.
Randoms.
Randoms should be estimated from the delayed sinograms by totaling all counts within a 12-cm radius of the center. Exactly the same sinogram bins should be used for this calculation as for trimming the prompts sinogram above. The randoms counting rate, Rr,i,j, for slice i and acquisition j is computed from:
 Eq. 1 where CTOT,i,jdelayeds is the total number of events within the 12-cm radius in the delayed sinogram, and Tacq,j is the duration of the acquisition. Our notation follows that of NU 2-2001.
Eq. 1 where CTOT,i,jdelayeds is the total number of events within the 12-cm radius in the delayed sinogram, and Tacq,j is the duration of the acquisition. Our notation follows that of NU 2-2001.
Intrinsic Trues.
In addition to the intrinsic randoms, a small intrinsic trues background occurs in LSO-based scanners as well, typically on the order of 100 cps or less within the shadow of the scatter phantom and fairly uniformly distributed. If not corrected for, this background would appear as a small contribution to scatter, noticeable at activities below about aref. If a final acquisition is made with no source present (but with the polyethylene cylinder still in place), then the intrinsic trues rate, Rint_trues,i, can be estimated from the prompts–delayeds within the 12-cm radius in the sinograms, as for the randoms:
 Eq. 2 where CTOT,i,no_sourceprompts–delayeds is the total number of events within the 12-cm radius in the prompts–delayeds sinogram acquired with no source present. We suggest that the total intrinsic trues rate within the shadow of the phantom, ∑i Rint_trues,i, be reported.
Eq. 2 where CTOT,i,no_sourceprompts–delayeds is the total number of events within the 12-cm radius in the prompts–delayeds sinogram acquired with no source present. We suggest that the total intrinsic trues rate within the shadow of the phantom, ∑i Rint_trues,i, be reported.
Scatter and Scatter Fraction.
The scatter counting rate, Rs,i,j, may be defined as the totals minus the trues, randoms, and intrinsic trues:
 Eq. 3 where RTOT,i,j and Rt,i,j are the total and true event counting rates, respectively, as defined in NU 2-2001. Equation 3 is not exactly correct at higher activities because of neglect of counting losses from Rint_trues,i, but the effect is negligible. The scatter fraction for each slice, SFi,j, may then be estimated as the ratio of scatter to the trues plus scatter:
Eq. 3 where RTOT,i,j and Rt,i,j are the total and true event counting rates, respectively, as defined in NU 2-2001. Equation 3 is not exactly correct at higher activities because of neglect of counting losses from Rint_trues,i, but the effect is negligible. The scatter fraction for each slice, SFi,j, may then be estimated as the ratio of scatter to the trues plus scatter:
 Eq. 4 and the system scatter fraction, SFj, is estimated from:
Eq. 4 and the system scatter fraction, SFj, is estimated from:
 Eq. 5
Eq. 5
In contrast to the standard NEMA procedure, we propose that these scatter fractions be computed as a function of the activity. The scatter fraction tends to increase slightly as the activity increases, likely because of pulse pileup effects in the detectors (5). The system scatter fraction as a function of activity should be reported up to the peak of the NECR.
NECR.
Using the randoms counting-rate estimate defined above, the NECR may be computed according to the NEMA formula:
 Eq. 6 where k = 0 when a noiseless estimate of randoms is used, and k = 1 when the variance of the randoms estimate is equal to its mean (as is approximately true for online randoms subtraction). Noise-free estimates for the scatter and intrinsic trues are assumed, although the intrinsic trues are usually negligible at activities above aref.
Eq. 6 where k = 0 when a noiseless estimate of randoms is used, and k = 1 when the variance of the randoms estimate is equal to its mean (as is approximately true for online randoms subtraction). Noise-free estimates for the scatter and intrinsic trues are assumed, although the intrinsic trues are usually negligible at activities above aref.
Sensitivity
For the sensitivity measurement (section 5), the NU 2-2201 criteria are that counting losses be <1% and that the RTR be <0.05. Thus, we recommend that the source activity be <aref (or s < sref) for all acquisitions. The data should be corrected for randoms using the delayed coincidence window technique. The data should also be corrected for intrinsic trues, using a background measurement with no external sources or phantoms present to estimate the intrinsic trues rate over the entire FOV, Rint_trues,iFOV, for each slice i. The corrected net trues rate for each acquisition j that should be used in the analysis is then:
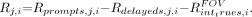 Eq. 7
Eq. 7
To ensure the quality of the data after randoms subtraction, we suggest acquiring 20% more counts during the test than the quantity specified by NU 2. We recommend that the total intrinsic trues rate, ∑i Rint_trues,iFOV, be reported here also.
CONCLUSION
An unavoidable radiation background is present on LSO-based PET tomographs, arising from the natural radioactivity of lutetium. The experimental techniques specified by the current NEMA NU 2 standards for measuring tomograph performance do not account for such a background and therefore cannot be applied to these machines strictly as written. Neglect of this background would lead to erroneous results for several of the tests. Nevertheless, we have shown that it is possible to achieve the purpose of the measurements with appropriate modifications to the recommended acquisition and analysis procedures. We have made several suggestions along these lines that we hope may be useful as a basis for applying NU 2-2001 to this class of scanners. These modifications are not intended to supplant the current standards for conventional tomographs without intrinsic radioactivity, however. Alternative approaches may exist, and the proposals made here are not sanctioned by NEMA at present.
The radioactivity of natural lutetium is the price that must be paid for the other benefits of LSO, such as its short scintillation decay time, high light output, and high stopping power. If measured appropriately using the procedures described here, the performance of current LSO systems is found to be consistent with what one would expect for a machine that has the improved live time and coincidence timing inherent in LSO but that is otherwise similar to conventional scanners, as shown in the accompanying article (6). The intrinsic background on such machines will be reduced further, but not eliminated entirely, as newer generations of detectors and electronics permit the use of more narrow energy acceptance windows around the photopeak of the annihilation radiation (7). Thus, the need to reconcile NU 2 with LSO-based scanners will remain.
Footnotes
Received Jun. 3, 2003; revision accepted Nov. 24, 2003.
For correspondence or reprints contact: Charles C. Watson, PhD, CPS Innovations, 810 Innovation Dr., Knoxville, TN 37932-2571.
E-mail: Charles.Watson{at}cpspet.com