Abstract
In calculations of absorbed doses from radioactive patients, the activity distribution in such patients is generally assumed to be an unattenuated point source and the dose to exposed individuals at a given distance is therefore calculated using the inverse square law. In many nuclear medicine patients, the activity distribution is widely dispersed and does not simulate a point source. In these cases, a line-source model is proposed to more accurately reflect this extended activity distribution. Methods: Calculations of dose rate per unit activity were performed for a point source and for line sources of lengths of 20, 50, 70, 100, and 174 cm, and the ratios of line-source values to point-source values were calculated. In addition, radionuclide-independent conversion factors, to convert exposure rate constants to dose rates per unit activity, for these line-source lengths at various distances were determined. Results: The calculated values, substantiated by published data, indicate that the inverse square law approximation is not valid for a line source until a certain distance is reached, dependent on the length of the line source. For the 20-, 50-, 70-, 100-, and 174-cm line sources, the dose rate values estimated by the inverse square law approximation are within approximately 10% of the values estimated using the line-source approach at distances of 20, 45, 60, 85, and 145 cm, respectively. At closer distances, use of the point-source model for a patient with an extended activity distribution will overestimate the radiation absorbed dose to exposed individuals, sometimes by a very significant amount. Conclusion: The line-source model is a more realistic and practical approach than the traditional point-source model for determining the dose to individuals exposed to radioactive patients with widespread activity distributions.
Patients receiving radiopharmaceuticals are radioactive sources, and calculating the radiation absorbed dose to nearby individuals is frequently necessary, especially for patients receiving therapeutic radiopharmaceuticals. Although it is expected that radioactive patients are counseled to stay a reasonable distance from others, there are often specific situations that need to be addressed, such as doses to others while sleeping, using public or private transportation, or being in a theater for a few hours. In addition, calculating radiation absorbed dose to individuals exposed to diagnostic nuclear medicine patients is often prudent, if only to reassure patients, their families, and their caregivers. Patients who are mothers with young children are especially apprehensive about radiation and often want to know the potential dose to their children. In such calculations, the activity distribution in the patient is usually assumed to be an unattenuated point source, and the dose to exposed individuals at a given distance is therefore calculated under the assumption that the dose varies inversely as the square of the distance from the patient. If appropriate patient attenuation correction is performed, this inverse square relationship is essentially correct in the case of hyperthyroid patients, for example, in whom significant radioiodine uptake and prolonged retention is usually limited to the thyroid gland. However, this relationship is not valid and yields an overestimate of the dose, in the general case of patients receiving radionuclide therapy, such as palliative treatment of bony metastases or radioimmunotherapy. In such patients, the activity is more widely distributed (1–3). In radioimmunotherapy, most of the activity is located within the torso, and in radionuclide therapy involving bone disease, the activity may be located along the entire length of the patient. It is proposed that a line-source model with attenuation correction, using the measured dose rate, be used for these cases that involve more widespread activity distributions. We realize that other models may be even more accurate, but we are limiting this study to the line-source approximation because it is more accurate than the point-source model, is conservative, and can easily be routinely implemented.
MATERIALS AND METHODS
The dose to an individual exposed to a radioactivity-containing patient can be estimated using a point-source model by the following equation (1,4):
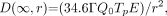 Eq. 1 where D(∞,r) is the total dose (actually, the total dose equivalent in mSv or mrem) to others from exposure to the photon radiation at a distance r (cm) from the patient, Γ is the exposure rate constant of the radionuclide (mSv cm2/MBq h or mrem cm2/mCi h), Q0 is the administered activity (MBq or mCi), Tp is the physical half-life of the radionuclide (d), and E is the occupancy factor. Equation 1 is applicable only for the specific case of infinite decay and a single occupancy factor. When more general conditions exist, such as variable exposure times and occupancy factors, modifications must be made. Equation 1 is usually solved for dose at a distance of 1 m, although any distance can be used. If measurements of biologic elimination of the radioactive material from the patient are made, as they should be especially if the radiopharmaceutical is significantly eliminated from the body through biologic processes, the effective half-life Te should be used in place of the physical half-life Tp. The exposure rate constant Γ is strictly a measure of exposure rate and not the total effective dose equivalent as specified in Regulatory Guide 8.39 (2) of the Nuclear Regulatory Commission, because Γ does not account for attenuation and scatter in the patient or exposed individual. In addition, Equation 1 assumes than an exposure of 2.58 × 10−4 C/kg (1 R) is an effective dose equivalent of 1 cSv (1 rem). Estimates of attenuation and tissue shielding by the patient may be accounted for through theoretic calculation by multiplying Γ by an appropriate factor to correct for patient attenuation and scatter or by measurement of actual patient dose rates. The dose rate at a given distance is theoretically equal to the Γ Q0/r2 term in Equation 1, and, if measured, the measured dose rate should be used in place of this term. There is no need to further correct the measured dose rate for patient attenuation because the measurement incorporates patient attenuation. Although the additional step of measuring the actual dose rate at a specified distance more accurately estimates the dose to exposed individuals, the calculation of the dose at other than the measurement distance still assumes an inverse square dose-distance relationship.
Eq. 1 where D(∞,r) is the total dose (actually, the total dose equivalent in mSv or mrem) to others from exposure to the photon radiation at a distance r (cm) from the patient, Γ is the exposure rate constant of the radionuclide (mSv cm2/MBq h or mrem cm2/mCi h), Q0 is the administered activity (MBq or mCi), Tp is the physical half-life of the radionuclide (d), and E is the occupancy factor. Equation 1 is applicable only for the specific case of infinite decay and a single occupancy factor. When more general conditions exist, such as variable exposure times and occupancy factors, modifications must be made. Equation 1 is usually solved for dose at a distance of 1 m, although any distance can be used. If measurements of biologic elimination of the radioactive material from the patient are made, as they should be especially if the radiopharmaceutical is significantly eliminated from the body through biologic processes, the effective half-life Te should be used in place of the physical half-life Tp. The exposure rate constant Γ is strictly a measure of exposure rate and not the total effective dose equivalent as specified in Regulatory Guide 8.39 (2) of the Nuclear Regulatory Commission, because Γ does not account for attenuation and scatter in the patient or exposed individual. In addition, Equation 1 assumes than an exposure of 2.58 × 10−4 C/kg (1 R) is an effective dose equivalent of 1 cSv (1 rem). Estimates of attenuation and tissue shielding by the patient may be accounted for through theoretic calculation by multiplying Γ by an appropriate factor to correct for patient attenuation and scatter or by measurement of actual patient dose rates. The dose rate at a given distance is theoretically equal to the Γ Q0/r2 term in Equation 1, and, if measured, the measured dose rate should be used in place of this term. There is no need to further correct the measured dose rate for patient attenuation because the measurement incorporates patient attenuation. Although the additional step of measuring the actual dose rate at a specified distance more accurately estimates the dose to exposed individuals, the calculation of the dose at other than the measurement distance still assumes an inverse square dose-distance relationship.
For a line-source model, the falloff in dose is more complicated (5,6) than for a point source. It is a function of the angle in radians subtended by the length of the line source and the perpendicular distance from the line to the target individual:
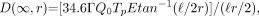 Eq. 2 where ℓ is the length of the line source in centimeters.
Eq. 2 where ℓ is the length of the line source in centimeters.
As Equation 2 indicates, the distance-dependent dose rate for a line source is dependent on the length of the source, and the inverse square term, 1/r2, for the point-source model is replaced by an arctangent term, tan−1 (ℓ/2r)]/(ℓ r/2). Estimates of attenuation and tissue shielding by the patient may be accounted for through theoretic calculation by multiplying the exposure rate constant Γ by [1 − φ(TB←TB)], as described by Zanzonico et al. (7), or by 0.6 for the specific case of 131I (8) or by measurement of actual patient dose rates. The dose rate is theoretically equal to the [Γ Q0 tan−1 (ℓ/2r)]/(ℓ r/2)] term in Equation 2, and, if measured, the measured dose rate should be used in place of this term. In radioimmunotherapy, most of the activity is located within the torso, which, according to the mathematical phantom used in MIRD Pamphlet No. 5, Revised (9), is 70 cm in length for a standard adult. In radionuclide therapy involving bone disease, the activity may be located along the entire length of the patient; the standard adult height used in the MIRD mathematical phantom is 174 cm (9). Calculations of dose rate per unit activity were therefore performed for a point source and for line sources of lengths of 20, 50, 70, 100, and 174 cm (the 20-, 50-, and 100-cm lengths were selected to add flexibility for the user) at various distances up to 100 cm, and the ratios of line-source values to point-source values were calculated. In addition, radionuclide-independent conversion factors, to convert exposure rate constants to dose rates per unit activity, for these line-source lengths at various distances were determined.
RESULTS
The ratios of line-source values to point-source values as a function of distance and line-source length are shown in Table 1. These values are radionuclide independent; thus, the ratios for each given line-source model directly indicate the point-source model agreement at each distance for any radionuclide. The values in Table 1 indicate that the inverse square law approximation is not valid for a line source until a certain distance is reached, dependent on the length of the line source. For the 20-, 50-, 70-, 100-, and 174-cm line sources shown in Table 1, the dose rate values estimated by the inverse square law approximation are within approximately 10% of the values estimated using the line-source approach at distances of 20, 45, 60, 85, and 145 cm (not shown in Table 1), respectively. At closer distances, use of the point-source model for a patient with an extended activity distribution overestimates dose rate and, accordingly, overestimates the radiation absorbed dose to exposed individuals, sometimes by a very significant amount.
Ratios of Line-Source Values to Point-Source Values as Function of Line-Source Length and Distance
Radionuclide-independent conversion factors (cm−2), to convert exposure rate constants Γ (mSv cm2/MBq h or mrem cm2/mCi h) to dose rates per unit activity (mSv/MBq h or mrem/mCi h) at a given distance for the various line-source lengths, are given in Table 2. Dose rates per unit activity at a given distance, for any radionuclide, can be determined from Table 2 by simply multiplying the values by the appropriate exposure rate constant. Of course, these values are theoretic; they must be corrected for patient attenuation and scatter. If patient dose rates at a given distance are measured, then dose rate values at any other distance can be obtained directly from Table 2 for the appropriate line-source length by simply multiplying the measured dose rate by the ratio of the value given in Table 2 for that measurement distance and the value for any other distance desired. For example, suppose you measure the dose rate at 1 m from a patient containing a source of activity that is distributed in the patient’s torso and you desire to estimate the dose rate at a distance of 10 cm from the patient. In this case, you would multiply the measured dose rate by 38.4 (using the 70-cm line-source column, divide the 3.69 × 10−3 value at 10 cm by the 9.62 × 10−5 value at 100 cm). If the distance-dependent dose rate had been calculated using the inverse square relationship, the measured dose rate at 1 m would have been multiplied by 100 (1002/102) to estimate the dose rate at 10 cm. In this case, an unreasonably high dose estimate, unnecessarily conservative by a factor of 2.6 (100/38.4), would result.
Radionuclide-Independent Conversion Factors
DISCUSSION
Although it is common practice to measure the dose rate at 1 m from a radioactive patient (most commonly, a radionuclide therapy patient) and then use the inverse square dose-distance approximation to estimate the dose rate at other distances, this approach can lead to large dose overestimates if the radioactivity is widely distributed in the patient. A practical method for calculating the radiation dose to exposed individuals based on modeling the patient as a line source, with or without any measurement of patient dose rate, has been described. A lookup table has been provided as an essential tool for ease of implementation of this calculational algorithm. When the distances of interest are known, it may be preferable to obtain additional dose rate measurements. However, many times these distances are not known a priori and dose rate measurements are not available, or if many distances are required it may not be practical to obtain all the required dose rate measurements.
The line-source model is still conservative because of the continued lack of attenuation correction in the exposed individual. Anthropomorphic mathematical phantoms with state-of-the-art Monte Carlo transport techniques have been proposed for determining appropriate correction factors to apply to dose rate measurements to account for attenuation and scatter in the exposed individual (10). For example, Monte Carlo simulations have indicated that for 131I, the measured dose rate at 1 m, which reflects only the surface entrance dose rate to the exposed individual, should be multiplied by 0.62 to correctly reflect the total-body dose rate (10). A simpler technique would be to multiply the measured dose rate by an attenuation factor for the exposed individual, such as (1 − e−μT/2), where μ is the linear attenuation coefficient of the pertinent radionuclide and T is the body thickness of the exposed individual. Ultimately, the dose calculations should be performed using a modification of the MIRD dosimetry schema (11), applying the cumulated activity in the patient and an appropriate total body-to-total body S value taking into account the patient and the exposed individual. Mathematical phantoms now exist not only for adults but also for both children and pregnant women, thus allowing a more accurate dose calculation scheme (12,13). Radionuclide total body-to-total body S values (i.e., patient-to-exposed individual total body-to-total body S values) should be developed for this purpose, in an attempt to bring external radiation dose calculations into the same routine use as has been achieved for internal radiation dose calculations.
CONCLUSION
Radiation dose estimates to individuals exposed to radioactivity-containing patients are important for a variety of dose reconstruction scenarios and also for determining the times necessary for the patient to avoid certain behaviors, such as holding babies, approaching pregnant women, and sleeping with a partner. Because each radionuclide therapy patient who is released must be given written instructions to maintain doses to members of the public as low as is reasonably achievable, use of the line-source model to estimate absorbed dose to exposed individuals should lead to a more rational formulation of postrelease precautions, potentially resulting in the reduction of unnecessarily burdensome radiation safety advice to the patient, unnecessary concern for certain members of the public, and unnecessary regulatory paperwork.
Footnotes
Received Nov. 8, 2001; revision accepted May 21, 2002.
For correspondence or reprints contact: Jeffry A. Siegel, PhD, Nuclear Physics Enterprises, 216 Society Hill, Cherry Hill, NJ 08003.
E-mail: siegelja{at}aol.com






