Visual Abstract
Abstract
Tracer kinetic modeling in dynamic PET has the potential to improve the diagnosis, prognosis, and research of lung diseases. The advent of total-body PET systems with much greater detection sensitivity enables high-temporal-resolution (HTR) dynamic PET imaging of the lungs. However, existing models may become insufficient for modeling the HTR data. In this paper, we investigate the necessity of additional corrections to the input function for HTR lung kinetic modeling. Methods: Dynamic scans with HTR frames of as short as 1 s were performed on 13 healthy subjects with a bolus injection of about  of 18F-FDG using the uEXPLORER total-body PET/CT system. Three kinetic models with and without time-delay and dispersion corrections were compared for the quality of lung time–activity curve fitting using the Akaike information criterion. The impact on quantification of 18F-FDG delivery rate
of 18F-FDG using the uEXPLORER total-body PET/CT system. Three kinetic models with and without time-delay and dispersion corrections were compared for the quality of lung time–activity curve fitting using the Akaike information criterion. The impact on quantification of 18F-FDG delivery rate  , net influx rate
, net influx rate  and fractional blood volume
and fractional blood volume  was assessed. Parameter identifiability analysis was also performed to evaluate the reliability of kinetic quantification with respect to noise. Correlation of kinetic parameters with age was investigated. Results: HTR dynamic imaging clearly revealed the rapid change in tracer concentration in the lungs and blood supply (i.e., the right ventricle). The uncorrected input function led to poor time–activity curve fitting and biased quantification in HTR kinetic modeling. The fitting was improved by time-delay and dispersion corrections. The proposed model resulted in an approximately 85% decrease in
was assessed. Parameter identifiability analysis was also performed to evaluate the reliability of kinetic quantification with respect to noise. Correlation of kinetic parameters with age was investigated. Results: HTR dynamic imaging clearly revealed the rapid change in tracer concentration in the lungs and blood supply (i.e., the right ventricle). The uncorrected input function led to poor time–activity curve fitting and biased quantification in HTR kinetic modeling. The fitting was improved by time-delay and dispersion corrections. The proposed model resulted in an approximately 85% decrease in  , an approximately 75% increase in
, an approximately 75% increase in  , and a more reasonable
, and a more reasonable  (∼0.14) than the uncorrected model (∼0.04). The identifiability analysis showed that the proposed models had good quantification stability for
(∼0.14) than the uncorrected model (∼0.04). The identifiability analysis showed that the proposed models had good quantification stability for 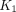 ,
,  , and
, and  . The
. The  estimated by the proposed model with simultaneous time-delay and dispersion corrections correlated inversely with age, as would be expected. Conclusion: Corrections to the input function are important for accurate lung kinetic analysis of HTR dynamic PET data. The modeling of both delay and dispersion can improve model fitting and significantly impact quantification of
estimated by the proposed model with simultaneous time-delay and dispersion corrections correlated inversely with age, as would be expected. Conclusion: Corrections to the input function are important for accurate lung kinetic analysis of HTR dynamic PET data. The modeling of both delay and dispersion can improve model fitting and significantly impact quantification of 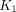 ,
,  , and
, and  .
.
PET with 18F-FDG or other radiotracers is a promising method for studying a variety of lung diseases, including lung cancer (1), acute lung injury (2,3), asthma (4), lung fibrosis (5), and recently coronavirus disease 2019 (6). The SUV is a traditional semiquantitative measure for evaluating lung 18F-FDG uptake (7,8), whereas kinetic analysis through compartment modeling (9) has shown the potential to provide more quantitative tracer kinetics, for example, the 18F-FDG delivery rate  (10), net influx rate
(10), net influx rate  (11–15), and fractional blood volume
(11–15), and fractional blood volume 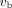 (13,16), to better characterize lung diseases in previous human and animal studies. However, conventional PET scanners have a relatively poor sensitivity and limited temporal resolution (e.g., 10–40 s/frame) for dynamic imaging, which in turn affects the performance of lung kinetic quantification.
(13,16), to better characterize lung diseases in previous human and animal studies. However, conventional PET scanners have a relatively poor sensitivity and limited temporal resolution (e.g., 10–40 s/frame) for dynamic imaging, which in turn affects the performance of lung kinetic quantification.
The advent of the uEXPLORER (United Imaging) total-body PET and other scanners with a long axial field of view (17–19) has brought new opportunities to improve lung kinetic modeling by offering a large axial field of view to cover the entire lungs with improved detection efficiency, allowing high-temporal-resolution (HTR) imaging, such as with 1 s or even a subsecond per frame (20,21). The HTR ability is especially useful for capturing the rapidly changing early phase of tracer uptake in lung tissues. Meanwhile, image-derived input functions (IDIFs) can also be extracted with HTR from major blood pools (e.g., ventricles and large blood vessels) for kinetic modeling (21,22). In this work, we investigate the use of HTR data for lung kinetic quantification with total-body PET, expecting improvement especially for those parameters that are sensitive to the early kinetics, such as 18F-FDG  and
and  .
.
One challenge with using HTR data is the potential need for additional corrections for the IDIF. Recent work on total-body PET kinetic modeling has considered time-delay correction to account for the difference between the tracer arrival time in a tissue and the arrival in the blood pool, where the IDIF is extracted (21–23). However, dispersion (24,25) may also occur when the tracer travels from the location at which the IDIF is determined to the capillaries of the lungs. The correction for either time delay or dispersion has only rarely been investigated in previous studies of lung kinetic modeling and is usually omitted (2,26–28), partly because of the limited temporal resolution (e.g., 10 s/frame) of conventional dynamic PET. Here, we hypothesize that a simultaneous correction for both the time-delay and dispersion effects is essential for accurate kinetic modeling in HTR dynamic PET imaging of the lungs.
MATERIALS AND METHODS
HTR Dynamic Data Acquisition on uEXPLORER
Thirteen healthy human subjects (age [mean±SD], 49 ± 15 y; weight 82 ± 18 kg; 6 men, 7 women) gave written informed consent and were scanned on a uEXPLORER total-body PET/CT system (29,30). The study was approved by the Institutional Review Board at the University of California, Davis. After an ultralow-dose CT scan (140 kVp, 5 mAs), each participant underwent a dynamic 18F-FDG PET scan with intravenous bolus administration of a dose of approximately 370 MBq. Total-body PET imaging was performed for 60 min starting immediately before the injection. The resulting list-mode data were reconstructed into dynamic images using the vendor-supplied time-of-flight ordered-subset expectation maximization algorithm with 4 iterations and 20 subsets and a voxel size of  3. The dynamic framing protocol contains 120 frames over 60 min:
3. The dynamic framing protocol contains 120 frames over 60 min:  with HTR frames (1–2 s/frame) over the first 2 min. For each subject, a region of interest (ROI) was placed in the right ventricle to extract an IDIF
with HTR frames (1–2 s/frame) over the first 2 min. For each subject, a region of interest (ROI) was placed in the right ventricle to extract an IDIF  to represent the pulmonary blood supply, the dominant blood input to the lungs (31,32). Five ROIs were placed in the left and right lungs (1 in each of the 5 lung lobes) to extract lung time–activity curves from the dynamic images with diminished effects of motion and spillover. The 5 lung-ROI time–activity curves were averaged to generate a global lung time–activity curve
to represent the pulmonary blood supply, the dominant blood input to the lungs (31,32). Five ROIs were placed in the left and right lungs (1 in each of the 5 lung lobes) to extract lung time–activity curves from the dynamic images with diminished effects of motion and spillover. The 5 lung-ROI time–activity curves were averaged to generate a global lung time–activity curve  for each of the 13 subjects. An additional ROI was also placed in the left ventricle to extract the time–activity curve
for each of the 13 subjects. An additional ROI was also placed in the left ventricle to extract the time–activity curve  for the purpose of comparison. In addition to the HTR time–activity curves, time–activity curves of low temporal resolution were generated using 10 s/frame for the first 3 min for all the ROIs.
for the purpose of comparison. In addition to the HTR time–activity curves, time–activity curves of low temporal resolution were generated using 10 s/frame for the first 3 min for all the ROIs.
Compartmental Modeling
18F-FDG kinetics in the extravascular lung is described by a 2-tissue irreversible (2Ti) compartmental model (33) and is illustrated in Figure 1A. Suppose that  is the blood input function and that
is the blood input function and that  and
and  are the concentration of free and phosphorylated 18F-FDG in the extravascular lung tissue. We would then have the following differential equations to describe the system states:
are the concentration of free and phosphorylated 18F-FDG in the extravascular lung tissue. We would then have the following differential equations to describe the system states: Eq. 1where
Eq. 1where  (mL/min/cm3) and
(mL/min/cm3) and  (/min) indicate the blood-to-tissue and tissue-to-blood 18F-FDG delivery rate constants, respectively.
(/min) indicate the blood-to-tissue and tissue-to-blood 18F-FDG delivery rate constants, respectively.  (/min) is the 18F-FDG phosphorylation rate constant. This irreversible model assumes that the dephosphorylation process is negligible (i.e., the dephosphorylation rate constant
(/min) is the 18F-FDG phosphorylation rate constant. This irreversible model assumes that the dephosphorylation process is negligible (i.e., the dephosphorylation rate constant  ) (13). The 18F-FDG concentration in lung parenchyma,
) (13). The 18F-FDG concentration in lung parenchyma,  , is the summation of the free and the phosphorylated 18F-FDG,
, is the summation of the free and the phosphorylated 18F-FDG, Eq. 2where
Eq. 2where 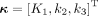 , ⊗ denotes the convolution operation, and
, ⊗ denotes the convolution operation, and 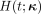 is the impulse response function of the 2Ti model:
is the impulse response function of the 2Ti model: Eq. 3
Eq. 3
(A) Compartmental model of lung kinetics. (B) Proposed IDIF-T model with correction of time delay in input function. (C) Proposed IDIF-T-D model with both time-delay and dispersion corrections included.
The measured lung time–activity curve obtained by PET is modeled by  , a mixture of the blood compartment and the tissue compartment,
, a mixture of the blood compartment and the tissue compartment, Eq. 4
Eq. 4 is the whole blood activity and is usually approximated by
is the whole blood activity and is usually approximated by  for 18F-FDG.
for 18F-FDG.
Following previous studies (2,34,35), the right ventricle IDIF can be used for the blood input, Eq. 5because the pulmonary circulation accounts for most of the total blood input to the lung (32).
Eq. 5because the pulmonary circulation accounts for most of the total blood input to the lung (32).
The measured lung time–activity curve  was fitted with the model time–activity curve
was fitted with the model time–activity curve  using a nonlinear least-squares formulation:
using a nonlinear least-squares formulation: Eq. 6where
Eq. 6where denotes the weighted residual sum of squares of the curve fitting. θ is the unknown parameter set,
denotes the weighted residual sum of squares of the curve fitting. θ is the unknown parameter set,  .
.  is the time of the m-th frame in a total of M frames, and
is the time of the m-th frame in a total of M frames, and  is the weight for frame m considering the time length and nuclear decay (36):
is the weight for frame m considering the time length and nuclear decay (36): Eq. 7
Eq. 7
Here  is the length of the m-th frame,
is the length of the m-th frame,  is the decay constant, and the half-life
is the decay constant, and the half-life  for 18F-FDG. This time-varying weight was based on our initial studies of model fitting.
for 18F-FDG. This time-varying weight was based on our initial studies of model fitting.
Modeling of Time-Delay Effect
Corrections for time delay were seldom considered in previous studies of lung kinetic modeling (2,26–28) because the delay was usually only several seconds and tended to be blurred out by conventional dynamic imaging of limited temporal resolution (e.g., 10 s/frame). However, the time-delay effect will no longer be concealed with the HTR measurement (e.g., 1 s/frame) and is likely to affect parameter quantification if not accounted for.
To model the time-delay effect of the IDIF extracted from the right ventricle, we include a time-delay parameter  (s) in the input function (Fig. 1B):
(s) in the input function (Fig. 1B):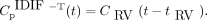 Eq. 8
Eq. 8
The proposed input function model with time-delay correction is noted as IDIF-T. The time-delay parameter  is included in θ and will be jointly estimated with other kinetic parameters during time–activity curve fitting.
is included in θ and will be jointly estimated with other kinetic parameters during time–activity curve fitting.
Simultaneous Correction for Dispersion
Dispersion may occur when the tracer travels from the right ventricle to the lung capillaries. Here, we model the actual lung blood input as the convolution of the measured IDIF with a parameterized dispersion function following Iida’s monoexponential form (24,37), Eq. 9
Eq. 9
This input function model is denoted as IDIF-T-D (Fig. 1C), in which both the dispersion parameter  (/min) and time delay
(/min) and time delay  (s) are included in θ for joint parameter estimation.
(s) are included in θ for joint parameter estimation.
Note that here the simultaneous dispersion correction is different from those explored for brain PET (25). Previous work focused on a backward dispersion-correction problem (24,25). The measured input function, such as by arterial blood sampling from the radial artery, is a dispersed version of the actual input function. Therefore, the dispersion needs to be removed from the measured input function. In comparison, our work here is a forward dispersion-correction problem. The actual lung input function is a dispersed version of the measured IDIF, to which the dispersion needs to be added.
Evaluation of Time–Activity Curve Fit Quality
The Akaike information criterion (AIC) was used to compare the statistical fit quality of different models (38,39), Eq. 10where N is the number of unknown parameters to be optimized in θ and M is the number of dynamic frames. AIC reflects the trade-off between the goodness of fit and the simplicity of the model and thus accounts for the difference in the number of parameters that need to be estimated. A lower AIC value indicates better fitting quality.
Eq. 10where N is the number of unknown parameters to be optimized in θ and M is the number of dynamic frames. AIC reflects the trade-off between the goodness of fit and the simplicity of the model and thus accounts for the difference in the number of parameters that need to be estimated. A lower AIC value indicates better fitting quality.
Evaluation of the Impact on Kinetic Quantification
We evaluated the impact of the corrections on the quantification of 3 kinetic parameters of interest: 18F-FDG delivery rate K1, net influx rate Ki, and fractional blood volume  .
.  was calculated from the microparameters:
was calculated from the microparameters: Eq. 11
Eq. 11
The change in each kinetic parameter by a given model was reported relative to the parameter estimate by the standard IDIF model, and the reason for the quantification changes was studied by analyzing the time–activity curve fittings of different models.
Identifiability Analysis of Kinetic Parameter Estimates
As the proposed models have more parameters to estimate than the standard 2Ti model with the uncorrected IDIF, their kinetic parameter identifiability may be a concern. That is because a more complex model is more likely to be sensitive to random noise and may have reduced parameter stability. To evaluate the parameter identifiability, a noisy lung tissue time–activity curve  was simulated using a time-varying gaussian model (40–42):
was simulated using a time-varying gaussian model (40–42): Eq. 12where
Eq. 12where  is the m-th frame of the noise-free time–activity curve generated by the curve fitting of the tested model.
is the m-th frame of the noise-free time–activity curve generated by the curve fitting of the tested model.  is the scaling factor controlling the noise level and
is the scaling factor controlling the noise level and  is the unscaled standard deviation given by:
is the unscaled standard deviation given by: Eq. 13
Eq. 13
 was estimated using the residual error between the measured
was estimated using the residual error between the measured  and the modeled
and the modeled  using the model that demonstrated the best fitting by assuming that the fitting error of that model comes mostly from random noise. We simulated 500 noisy lung tissue time–activity curve realizations for each
using the model that demonstrated the best fitting by assuming that the fitting error of that model comes mostly from random noise. We simulated 500 noisy lung tissue time–activity curve realizations for each  and analyzed the bias and noise SD of each parameter estimate. The analysis was conducted for the 3 models (i.e., the IDIF, IDIF-T, and IDIF-T-D) using the HTR data. By summing the corresponding HTR frames together, the IDIF model using a more conventional low temporal resolution (10 s/frame in the first 3 min) was also included for comparison.
and analyzed the bias and noise SD of each parameter estimate. The analysis was conducted for the 3 models (i.e., the IDIF, IDIF-T, and IDIF-T-D) using the HTR data. By summing the corresponding HTR frames together, the IDIF model using a more conventional low temporal resolution (10 s/frame in the first 3 min) was also included for comparison.
Correlation of Lung 18F-FDG Kinetics with Age
Aging effects are evident in healthy lungs. Previous human studies have observed an inverse relationship between age and pulmonary blood volume (43,44). Therefore, we hypothesize that the  in the lungs tends to decrease with aging. Although we do not have longitudinal data on individuals in this study, we aim to explore any association between the 18F-FDG kinetic parameters and age using the available healthy subject cohort. We performed the Pearson regression analysis between age and kinetic parameters. Body mass index was also included in the regression to consider potential confounding factors.
in the lungs tends to decrease with aging. Although we do not have longitudinal data on individuals in this study, we aim to explore any association between the 18F-FDG kinetic parameters and age using the available healthy subject cohort. We performed the Pearson regression analysis between age and kinetic parameters. Body mass index was also included in the regression to consider potential confounding factors.
Demonstration of Total-Lung Parametric Imaging
In addition to the ROI-based kinetic analysis, we implemented the proposed kinetic modeling approach voxel by voxel. Parametric images of different kinetic parameters (e.g.,  , and
, and  ) were then generated for the entire lung. Kernel smoothing was applied to both the dynamic images and the parametric images for noise reduction (23).
) were then generated for the entire lung. Kernel smoothing was applied to both the dynamic images and the parametric images for noise reduction (23).
RESULTS
Example of HTR Dynamic Images and Time–Activity Curves
Figure 2 shows the acquired HTR total-body dynamic data for a representative subject. The 18F-FDG dynamics in the very early phases after injection were captured by the HTR, as illustrated by the total-body maximum-intensity projections of the SUV image in the coronal direction (Fig. 2A) and the HTR time–activity curves (Fig. 2B). To begin, the tracer was injected into a vein in the right arm before traveling to the right ventricle through the vena cava (Fig. 2A, 6–7 s of the scan time). The tracer next traveled through the pulmonary circulation by flowing into the lungs via the pulmonary artery (Fig. 2A, 9–10 s) and flowing out of the lungs to the left ventricle through the pulmonary veins (Fig. 2A, 14–15 s).
(A) HTR (1 s/frame) total-body 18F-FDG dynamic images of example subject acquired using uEXPLORER system. (B) Regional time–activity curves extracted from HTR dynamic images. y-axis on left is for time–activity curves of right ventricle and left ventricle, whereas y-axis on right is for time–activity curve of lung tissue, which has lower range by factor of 10. (C) Conventional low-temporal-resolution (10 s/frame) regional time–activity curves. LV = left ventricle; RV = right ventricle.
As a comparison, time–activity curves with the conventional temporal resolution are shown in Figure 2C. With a 10-s temporal resolution, the time–activity curves have lost much of the information about the early-phase 18F-FDG kinetics. Both the shape and the amplitude of the time–activity curves were distorted and inaccurate because of the poor temporal resolution.
Model Fitting of Lung Time–Activity Curve
The proposed approaches for modeling the input function can clearly impact the time–activity curve fitting, as shown by the fitting results for an example subject in Figure 3A along with the residual fitting errors in Figure 3B. These figures focus on the early dynamic phase, given that the late phase is similar among different models. Without the time-delay correction, the conventional IDIF model failed to fit the early-phase data even though the time delay is approximately 3 s (Supplemental Fig. 1A; supplemental materials are available at http://jnm.snmjournals.org). The dispersion correction in the IDIF-T-D model further improved the fitting of the first peak because it accounts for the deformation of the input function caused by the tracer dispersion effect (Supplemental Fig. 1B). The improved fitting by the proposed models (IDIF-T and IDIF-T-D) is further demonstrated by the decreased AIC (Fig. 3C; Table 1). The IDIF-T-D model achieved the best average AIC across all subjects.
(A) Effects of modeling time delay and dispersion on fitting of measured lung time–activity curve. (B) Effects on residual error of time–activity curve fitting. (C) AIC of different models in 13 subjects.
AIC Values of Different Kinetic Models Averaged from 13 Subjects
Kinetic Parameter Estimation
The means and SDs of lung kinetic parameters are reported in Table 2. Figure 4 shows the resulting impact on the quantification of  ,
,  , and
, and  .
.
Lung 18F-FDG Kinetic Quantification of  ,
,  ,
,  ,
,  , and
, and  Using Different Models
Using Different Models
Kinetic parameter estimates by different lung kinetic models (IDIF, IDIF-T, and IDIF-T-D).
When the IDIF model without time-delay or dispersion correction is used, the value of 0.350 ± 0.092 mL/min/cm3 seems unreasonable because of the poor fitting. This further supports that the direct application of the IDIF without corrections is not appropriate for the HTR data. The model IDIF-T was also likely to overestimate K1 given the poor early-phase fitting. The IDIF-T-D estimate of
value of 0.350 ± 0.092 mL/min/cm3 seems unreasonable because of the poor fitting. This further supports that the direct application of the IDIF without corrections is not appropriate for the HTR data. The model IDIF-T was also likely to overestimate K1 given the poor early-phase fitting. The IDIF-T-D estimate of  is 0.056 ± 0.033 mL/min/cm3, with an approximately 85% decrease compared with the conventional IDIF model. The IDIF-T-D model estimated
is 0.056 ± 0.033 mL/min/cm3, with an approximately 85% decrease compared with the conventional IDIF model. The IDIF-T-D model estimated  to be 0.144 ± 0.030, much higher than the estimate obtained with the IDIF (0.042 ± 0.022) and IDIF-T (0.107 ± 0.024) models. A previous study showed a blood fraction of 0.16 in the normal human lungs (13). Thus, the
to be 0.144 ± 0.030, much higher than the estimate obtained with the IDIF (0.042 ± 0.022) and IDIF-T (0.107 ± 0.024) models. A previous study showed a blood fraction of 0.16 in the normal human lungs (13). Thus, the  estimates by IDIF and IDIF-T are likely biased, whereas the estimates by IDIF-T-D are more consistent with the expected
estimates by IDIF and IDIF-T are likely biased, whereas the estimates by IDIF-T-D are more consistent with the expected  values. For
values. For  quantification, the proposed IDIF-T-D had an average increase of approximately 75% compared with the conventional IDIF model.
quantification, the proposed IDIF-T-D had an average increase of approximately 75% compared with the conventional IDIF model.
To understand the observed changes in parameter estimation, we analyzed the predicted activity of individual compartments (Supplemental Fig. 2). The vascular component  was much increased in the IDIF-T-D model as compared with the IDIF due to the increased
was much increased in the IDIF-T-D model as compared with the IDIF due to the increased  estimate. Therefore, the total extravascular component
estimate. Therefore, the total extravascular component  was decreased (Eqs. 2 and 4; Supplemental Fig. 2C), and
was decreased (Eqs. 2 and 4; Supplemental Fig. 2C), and  became smaller accordingly (Eq. 3). In addition,
became smaller accordingly (Eq. 3). In addition,  was higher in IDIF-T-D than in IDIF because of the increased
was higher in IDIF-T-D than in IDIF because of the increased  (Supplemental Fig. 2D), which was associated with decreased
(Supplemental Fig. 2D), which was associated with decreased  and
and  but increased
but increased  .
.
Identifiability of Kinetic Parameters
Table 3 shows the absolute value of relative bias and the SD of kinetic parameter estimates by different models. To clarify, this analysis is to study the robustness of models against random noise, whereas the systematic bias introduced by model oversimplification (e.g., neglecting the time-delay effect) is not involved. The HTR IDIF model had a lower bias and SD for  and
and  , along with worse Ki estimation, than the low-temporal-resolution IDIF. Among the HTR cases, both the IDIF-T-D and the IDIF models have a small bias (<2%) for
, along with worse Ki estimation, than the low-temporal-resolution IDIF. Among the HTR cases, both the IDIF-T-D and the IDIF models have a small bias (<2%) for  quantification, whereas the SD level of the IDIF-T-D (13.6%) was higher than that of the HTR IDIF (2.4%). The proposed IDIF-T-D model achieved a low bias (<1%) and a low SD (<3%) for quantifying
quantification, whereas the SD level of the IDIF-T-D (13.6%) was higher than that of the HTR IDIF (2.4%). The proposed IDIF-T-D model achieved a low bias (<1%) and a low SD (<3%) for quantifying  . For
. For  , the IDIF-T-D had bias (0.4%) and SD (6.2%) levels comparable to those of the HTR IDIF. The time-delay and dispersion parameters
, the IDIF-T-D had bias (0.4%) and SD (6.2%) levels comparable to those of the HTR IDIF. The time-delay and dispersion parameters 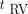 and
and  had good identifiability.
had good identifiability.
Relative Bias (Absolute Value) and SD of Kinetic Parameters in Identifiability Study
Correlation with Age
Figure 5 shows the correlation plots between age and 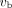 estimated by different approaches. For comparison, the result by a traditional low-temporal-resolution protocol (10 s/frame) is also included. Neither the
estimated by different approaches. For comparison, the result by a traditional low-temporal-resolution protocol (10 s/frame) is also included. Neither the  estimates by the low-temporal-resolution approach nor the
estimates by the low-temporal-resolution approach nor the  estimates by the HTR approaches without time-delay or dispersion correction showed a statistically significant correlation with age (all P > 0.1). In comparison, the
estimates by the HTR approaches without time-delay or dispersion correction showed a statistically significant correlation with age (all P > 0.1). In comparison, the  by the proposed IDIF-T-D model correlated with age with statistical significance (
by the proposed IDIF-T-D model correlated with age with statistical significance (
 . The observed age–
. The observed age– relationship is consistent with the results reported in previous studies (43,44) that show aging to be associated with decreased pulmonary blood volume. Neither age nor body mass index correlated with other kinetic parameters.
relationship is consistent with the results reported in previous studies (43,44) that show aging to be associated with decreased pulmonary blood volume. Neither age nor body mass index correlated with other kinetic parameters.
Correlation between subject age and  using standard IDIF model with 10 s/frame low temporal resolution (top left), IDIF model with 1 s/frame HTR (top right), IDIF-T model with HTR (bottom left), and proposed model IDIF-T-D with HTR (bottom right). LTR = low temporal resolution.
using standard IDIF model with 10 s/frame low temporal resolution (top left), IDIF model with 1 s/frame HTR (top right), IDIF-T model with HTR (bottom left), and proposed model IDIF-T-D with HTR (bottom right). LTR = low temporal resolution.
Demonstration of Total-Lung Parametric Images
Figure 6A shows the total-lung SUV and multiparametric images using the proposed IDIF-T-D model for a single subject. These images are overlaid on the corresponding CT image. The different parametric images demonstrate complementary spatial information. Figure 6B further shows the parametric images of  for a young subject (aged 26 y) and an old subject (aged 78 y). The lung
for a young subject (aged 26 y) and an old subject (aged 78 y). The lung  was much lower in this old subject than in the young subject. We also noticed that in the parametric images generated by the IDIF-T-D model, the posterior part of the lungs had a higher
was much lower in this old subject than in the young subject. We also noticed that in the parametric images generated by the IDIF-T-D model, the posterior part of the lungs had a higher  than the anterior part, and the posterior lung base had a higher
than the anterior part, and the posterior lung base had a higher  than the apex (Supplemental Fig. 3), which are also within expectation (45).
than the apex (Supplemental Fig. 3), which are also within expectation (45).
(A) 18F-FDG PET images of segmented lung for example subject (subject 4): SUV image of 55–60 min, and multiparametric images of 18F-FDG delivery rate 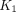 , fractional blood volume
, fractional blood volume  , and net influx rate
, and net influx rate  generated with IDIF-T-D model. These images are superimposed on corresponding CT images. (B)
generated with IDIF-T-D model. These images are superimposed on corresponding CT images. (B)  images of young subject (subject 3) and old subject (subject 1).
images of young subject (subject 3) and old subject (subject 1).
DISCUSSION
In this work, we studied the time-delay and dispersion corrections to the IDIF for lung kinetic modeling with HTR. Traditionally, limited by the temporal resolution of dynamic PET imaging, these corrections were not considered in most existing studies of pulmonary 18F-FDG kinetics (2,26,46), especially when the focus was on 18F-FDG  (2,13), a macroparameter of which the estimation is dominated more by the late-phase dynamic data and is expected to be less sensitive to these corrections. However, a model without these corrections resulted in a poor fitting performance for the HTR data acquired with total-body PET in this work (Figs. 3A and 3C).
(2,13), a macroparameter of which the estimation is dominated more by the late-phase dynamic data and is expected to be less sensitive to these corrections. However, a model without these corrections resulted in a poor fitting performance for the HTR data acquired with total-body PET in this work (Figs. 3A and 3C).
The proposed approaches to correcting time delay and dispersion for the IDIF led to much-improved lung time–activity curve fitting (Figs. 3A and 3B) with much lower AIC values (Table 1). Along with the improved fitting, the proposed modeling approaches had a significant impact on kinetic parameter quantification, especially for  and
and  (Table 2). This impact can be explained by the improved estimation of the vascular component in the fitted lung time–activity curves (Supplemental Fig. 2). We also noted that the time delay
(Table 2). This impact can be explained by the improved estimation of the vascular component in the fitted lung time–activity curves (Supplemental Fig. 2). We also noted that the time delay 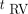 tended to correlate with the inverse of the dispersion parameter
tended to correlate with the inverse of the dispersion parameter  (
( ,
,  ) in the proposed model, as is consistent with the expectation that a longer time delay (larger
) in the proposed model, as is consistent with the expectation that a longer time delay (larger  ) is likely to be accompanied by a larger dispersion (smaller
) is likely to be accompanied by a larger dispersion (smaller  . Although the proposed model is more complex, the identifiability analysis results suggested the robustness of the proposed model to random noise (Table 3).
. Although the proposed model is more complex, the identifiability analysis results suggested the robustness of the proposed model to random noise (Table 3).
Although there is no ground truth, the  estimates by the proposed model are in general more consistent with the literature-reported pulmonary blood volume values and have led to an improved inverse correlation with age (Fig. 5). This correlation aligns with previous findings of decreased pulmonary capillary blood volume with aging (43,44). The same correlation would be otherwise missed if the conventional IDIF models with or without time-delay correction were used. Together with the improved time–activity curve fit quality (Fig. 3), our results here indicate the importance of simultaneous time-delay and dispersion corrections as compared with no correction or time-delay correction only (Fig. 5).
estimates by the proposed model are in general more consistent with the literature-reported pulmonary blood volume values and have led to an improved inverse correlation with age (Fig. 5). This correlation aligns with previous findings of decreased pulmonary capillary blood volume with aging (43,44). The same correlation would be otherwise missed if the conventional IDIF models with or without time-delay correction were used. Together with the improved time–activity curve fit quality (Fig. 3), our results here indicate the importance of simultaneous time-delay and dispersion corrections as compared with no correction or time-delay correction only (Fig. 5).
It is worth noting that simultaneous correction for time delay and dispersion was explored previously in dynamic brain PET studies (25). However, the method cannot be directly applied in our work on lung kinetic modeling because the prior study tackled a backward dispersion-correction problem that removes dispersion from the measured input function (e.g., from the radial artery), whereas this paper focuses on a forward dispersion-correction problem that adds dispersion to the measured IDIF for modeling the actual blood input. The latter approach is developed in response to the availability of IDIF in total-body HTR dynamic PET imaging.
In addition to the use of the right ventricle for deriving the IDIF, the region of the pulmonary arteries may be used directly for their closer location to the lung tissues. Similar results were obtained using the pulmonary arteries as the input function compared with using the right ventricle, including the input function after corrections (Supplemental Fig. 4A), lung time–activity curve fitting (Supplemental Fig. 4B), and kinetic parameter quantification (Supplemental Table 1), confirming the benefits of time-delay and dispersion corrections. The IDIFs from the left and right pulmonary arteries can also be used for kinetic modeling of individual lungs (Supplemental Table 1). However, use of the pulmonary arteries for IDIF needs to be done more carefully because the smaller size may make ROI placement more challenging to reduce the partial-volume effect.
This work has several limitations. First, the sample size is relatively small as the 13 healthy subjects vary in age and body weight. Second, subject motion can affect the kinetic quantification results (47). We tried to minimize the motion effect by carefully placing the ventricular ROIs to reduce the partial-volume effect of the myocardium. We also drew 5 ROIs in the lung lobes and extracted the global lung time–activity curve to decrease the respiratory motion effect and avoid a partial-volume effect from the liver. Third, the air fraction in the lungs may affect the absolute quantification of  and
and  (27,48), but the correction is not included here. It does not, however, influence the comparison of kinetic models because this tissue-fraction effect introduces only a scaling factor on
(27,48), but the correction is not included here. It does not, however, influence the comparison of kinetic models because this tissue-fraction effect introduces only a scaling factor on  and
and  and can be corrected after kinetic modeling.
and can be corrected after kinetic modeling.
Our future work will include a larger subject cohort and apply the method to study lung diseases, such as coronavirus disease 2019. The kinetic quantification approach can be also used to assess the lungs in other systemic diseases, for example, cancer and nonalcoholic fatty liver disease. Motion correction and air fraction correction will be implemented to optimize the HTR kinetic modeling and parameter estimation further. Another direction is to model the dual blood-input function to account for the fraction of tracer delivery from the bronchial circulation (49). This dual-input effect may be small in healthy lung tissues but can be significant in lung tumors (50), which will be explored in a future study.
CONCLUSION
We studied lung kinetic modeling for HTR dynamic PET imaging on the uEXPLORER total-body PET/CT system. Direct application of the standard IDIF model resulted in poor time–activity curve fitting. We developed an approach to jointly correcting the effects of time delay and dispersion in the IDIF. The proposed model greatly improved time–activity curve fitting and had a large impact on lung kinetic quantification. It also improved the correlation of  with age. Total-body HTR dynamic PET has the potential to be a sensitive tool for studying healthy lungs and lung diseases.
with age. Total-body HTR dynamic PET has the potential to be a sensitive tool for studying healthy lungs and lung diseases.
DISCLOSURE
This research is supported in part by National Institutes of Health grants R01 CA206187 and R01 DK124803. The University of California at Davis has a research agreement and revenue-sharing agreement with United Imaging Healthcare. No other potential conflict of interest relevant to this article was reported.
KEY POINTS
QUESTION: Is simultaneous correction of time delay and dispersion essential for high-temporal resolution kinetic modeling of the lungs in total-body dynamic PET imaging?
PERTINENT FINDINGS: The proposed time-delay and dispersion corrections can largely improve model fitting and have a significant impact on lung kinetic quantification, leading to an improved correlation between age and fractional blood volume  .
.
IMPLICATIONS FOR PATIENT CARE: Total-body dynamic PET with HTR kinetic modeling may offer a sensitive tool to evaluate the lungs in health and disease.
ACKNOWLEDGMENTS
We gratefully acknowledge the technologists and staff of the University of California, Davis, EXPLORER Molecular Imaging Center for acquiring and processing the data.
Footnotes
Published online Apr. 28, 2023.
- © 2023 by the Society of Nuclear Medicine and Molecular Imaging.
REFERENCES
- Received for publication August 22, 2022.
- Revision received February 22, 2023.














