Abstract
Accurate quantification in emission tomography is essential for internal radiopharmaceutical therapy dosimetry. Mean activity concentration measurements in objects with diameters less than 10 times the full width at half maximum of the imaging system’s spatial resolution are significantly affected (>10%) by the partial-volume effect. This study develops a framework for PET and SPECT spatial resolution characterization and proposes 2 MIRD recovery coefficient models—a geometric mean approximation (RECOVER-GM) and an empirical model (RECOVER-EM)—that provide shape-specific partial-volume correction (PVC). The models were validated using simulations and phantom experiments, with a comparative PVC test on ellipsoidal phantoms demonstrating that the RECOVER models significantly reduced error in activity quantification by factors of approximately 1.3–5.7 compared with conventional sphere-based corrections. The proposed recovery coefficient models and PVC methodology provide a robust framework for improved region-based PVC, including corrections for nonspherical tumor volumes. This work is part of the ongoing MIRDsoft.org project that aims to enhance accessibility to advanced dosimetry tools for improved disease characterization, treatment planning, and radiopharmaceutical therapy dosimetry.
- partial-volume effect
- resolution characterization
- recovery coefficient
- partial-volume correction
- dosimetry
- PET
- SPECT
In radiopharmaceutical therapy, the accurate quantification of absorbed dose is necessary for optimizing treatment efficacy, minimizing side effects, and assessing response to therapy (1). However, the limited spatial resolution of the SPECT and PET imaging systems and the digitization of the reconstructed images can lead to inaccurate activity quantification, particularly in small structures such as tumors. The partial-volume effect (PVE) leads to a systematic underestimation of the activity distribution in these images, directly hindering the accuracy of absorbed dose estimates derived from PET and SPECT images (2,3). In particular, the degree of PVEs is influenced by the object’s size and shape, the camera design and image reconstruction parameters, and the resolution of the reconstructed images (4).
To account for the apparent loss of activity due to the PVE and to improve the accuracy of activity quantification and absorbed dose estimates in vivo, partial-volume correction (PVC) methods have been developed (5,6). Traditionally, it is common practice to derive correction factors known as recovery coefficients (RCs) that represent the ratio of the measured activity concentration to the true activity concentration within a volume of interest (VOI). Conventional RC-based PVC (RC-PVC) methods typically involve calculating RCs from physical phantom experiments with varying volumes, often with spherical inserts, such as the National Electrical Manufacturers Association (NEMA) International Electrotechnical Commission (IEC) phantom. An empirical function is then fitted to the data to generate an RC curve as a function of volume. These volume-based RC curves can subsequently be applied to correct for PVEs (2,7). The RC-PVC method is suitable for routine clinical use because of its simplicity and ease of application (3).
A key limitation of conventional RC-based methods is that spherical corrections are applied to nonspherical targets. The degree of partial-volume losses depends on both the volume and shape of the object; for example, more compact shapes (e.g., spheres) are less affected by PVEs than are less compact shapes (e.g., ellipsoids), as their lower volume–to–surface area (V/SA) ratio reduces the amount of activity that “spills” in or out at the object edges (3). To account for this, various models have been developed to describe RCs as a function of resolution, volume, and shape (8–11). Recently, de Nijs developed an RC model for spheres and other shapes (8), which, for large volumes or high spatial resolution (RCs > 0.7), describes RCs with a single analytical equation for arbitrary shapes based on the V/SA ratio, formulated as a function of volume and sphericity. For lower RCs, de Nijs introduced an empirical equation requiring fits to shape-specific simulated data. A regime for which different shapes have the same RC for the same V/SA ratio was demonstrated (8,10,11). Grings et al. demonstrated through experimental analysis that, in 3-dimensional (3D)–printed kidney models, the V/SA ratio exhibits a direct proportionality to the loss in signal (10). Mínguez et al. further demonstrated this behavior in phantom experiments involving 3D-printed spheres and ellipsoids and derived an analytical equation describing theoretical spill-out RCs for spheres (11). Other studies (8,10,11) show that the V/SA ratio is more appropriate for parametrization of recovery than volume alone, suggesting this could potentially allow for more accurate PVC (8,11).
To generalize RC models and apply them for PVC, differences in spatial resolution across imaging systems and reconstruction protocols must be considered (8,11). Spatial resolution estimates in emission tomography are typically obtained through 2 distinct methods: (1) reconstructing point or line source experiments and calculating the full width at half maximum (FWHM) of a 1-dimensional Gaussian fit to line profiles drawn in the radial, axial, and tangential directions, and (2) creating a digital reference object (DRO) from a phantom acquisition and using a matched-filter analysis (MFA) to determine the FWHM of the Gaussian that minimizes the mean square error between the DRO and reconstructed image (12). Both methods have notable limitations: the point and line source approach does not consider object-dependent convergence or contrast ratios, whereas MFAs are susceptible to noise and registration errors and yield only a single global spatial resolution estimate. Additionally, neither method accounts for varying spatial resolution across different regions because of locally dependent convergence behavior. Accurate resolution estimates are essential for implementing RC models for PVC.
Motivated by the simplicity and broad applicability of conventional RC-PVC approaches, our objective in this study is to address the limitations of conventional RC-PVC methods and present a novel MIRD-RC model for both spheres and ellipsoids and extend the utility of the model to applications of resolution characterization and shape-specific PVC for improved quantitative accuracy and harmonization of absorbed dose estimates in radiopharmaceutical therapy.
BACKGROUND
RCs are defined as the proportion of activity concentration measured within a VOI to the true activity concentration within the source, measured within a VOI that delineates the physical boundary of the source. In PET and SPECT imaging, the measured RC (RCmeas) of a volume (V) is calculated (13):
Eq. 1where Cmeas is the mean activity concentration of the radionuclide measured within the object VOI, and Ctrue is the activity concentration of the radionuclide present in the object at the time of imaging. For objects in nonzero radioactive background, and under the assumption of linearity, RCmeas is a combination of spill-in (RCin) and spill-out (RCout) activity (14):
Eq. 2where OBR is the object-to-background ratio; for spheres, the OBR is commonly referred to as the sphere-to-background ratio (SBR). RCout is also often referred to as the contrast recovery coefficient (4). Common empirical functions fit to RC data are a monoexponential function fit to sphere radii versus RC data (15) or, more commonly, a volume dependent 2-parameter logistic (2-PL) function such as that presented in European Association of Nuclear Medicine (EANM) guidance documents (16).
Eq. 3where b1 and b2 are fitting parameters and V is the volume of the spherical phantom insert. The Gustafsson–Mínguez (11) equation describes the theoretical mean RCs for spherical objects under the assumption of a linear translation-invariant system; the equation is formulated as follows (8):
Eq. 4where σ is the SD of the Gaussian point-spread function, proportional to the FWHM such that 
. The equation describes RCs for spheres of any volume and resolution. Equation 4, along with other RC models such as the one presented in reference (8), can be used for region-based PVC by applying model-derived RCs to measured source region activities. When applying such corrections, it is important to account for both object spill-out and background spill-in PVEs. Accordingly, we can derive an expression for calculating the partial-volume corrected activity concentration (Ctrue,obj) for an object of interest using Equation 2. In this context, RCmeas in a phantom experiment is analogous to the measured activity concentration in the object (Cmeas,obj), where RCmeas = Cmeas,obj/Ctrue,obj. Similarly, the OBR for a source region is analogous to the OBR in Equation 2 and is equal to Ctrue,obj/Ctrue,bkg, with Ctrue,bkg representing the true activity concentration in the background. Assuming that the background is not significantly affected by PVEs, we can approximate Cmeas,bkg ≈ Ctrue,bkg, where Cmeas,bkg is the measured activity concentration in the background, local to the object VOI. Putting these definitions into Equation 2: 
Eq. 5RCout is derived using an RC model, for example, an RC curve (Eq. 3) or the Gustafsson–Mínguez equation (Eq. 4). It is important to note that this approach requires that the source region is accurately delineated so that the physical volume and shape can be determined. RC-PVC methods treat the activity within the VOI as uniform and returns a single mean corrected value (Ctrue,obj). An RC model that describes the PVEs of various shapes, combined with Equation 5, are essential pieces for a robust PVC methodology.
METHODS
A RC Model for Spheres
Theoretical RCout values were generated using Equation 4 for a range of spherical volumes (0.005–125 cm3) and Gaussian FWHMs (1–19 mm) to simulate different spatial resolutions. Motivated by prior work (8,10,11), we collapsed the RC data onto a single curve ([V/SA]/FWHM vs. RCout) and Microsoft Excel Solver’s generalized reduced gradient nonlinear fitting algorithm with a sum of squared differences objective function was used to fit a 2-PL function, of the form presented in Equation 3, to the data:
Eq. 6As highlighted previously (8), the 2-PL function did not adequately model the theoretical RCs. An improved empirical model was generated by fitting a 3-parameter logistic function (3-PL) of the form shown in Equation 7:
Eq. 7where β, γ, and L are fitting parameters. The resulting empirical model (Eq. 7) calculates RCout given the spatial resolution (Gaussian FWHM), spherical volume, and surface area. The RC curves fitted with Equations 6 and 7 were compared with the theoretical RCs (Eq. 4) by looking at the mean relative percent difference (MRD%) and mean absolute difference between the predicted (Eqs. 6 and 7) and theoretical RCs.
Extending the Model to Ellipsoids
Partial-volume losses for nonspherical tumors are suboptimally modeled by conventional spherical assumptions; a generalized RC model encompassing the variation in tumor shape could improve PVC accuracy. Prolate and oblate ellipsoids are defined as ellipsoids with 2 equal semidiameters (a = b); the semiaxis, a, is the equatorial radius of the ellipsoid, and c is the distance from center to pole along the symmetry axis. For c greater than a, the ellipsoid is prolate (pencil-like), and for c less than a, the ellipsoid is oblate (disk-like). For a equals c, the shape is a sphere. The surface area of an ellipsoid can be approximated using Equation 8 (8).
Eq. 8where a, b, and c are the lengths of the semiaxes and p is 1.6. A common property used to describe the compactness of ellipsoids is sphericity (ψ), defined as the ratio of a sphere’s surface area (of equal volume) to the surface area of the ellipsoid. Sphericity is independent of the volume of the ellipsoid, and spheres have a ψ equal to 1.
Finely sampled prolate or oblate ellipsoids of varying a:c ratios were generated in Python with a nominal activity concentration of 10 MBq/mL and were imported into ImageJ. RCout were generated for a range of simulated volumes by convolving the ellipsoids with an 18-mm FWHM Gaussian function (typical resolution of 177Lu SPECT reconstructed images (17)) using ImageJ’s “Gaussian Blur 3D” plugin. The RC was calculated as the ratio of mean activity concentration within the object boundary after convolution to the initial activity concentration. The RCs were plotted against (V/SA)/FWHM and V/FWHM3 to investigate if there was any relationship between sphericity and the prolate and oblate ellipsoid RCs. It was conceived that a new term could be added to Equation 7 to describe the RCs of prolate and oblate ellipsoids, and this is shown in Equation 9. We refer to this model as the REcovery COefficient equiValEnt Resolution empirical model (RECOVER-EM).
Eq. 9where V and SA are the ellipsoid’s volume and surface area, respectively. Equation 9 extends Equation 7 to accommodate prolate and oblate ellipsoids with the addition of a new term that acts on γ and L. This term, (2−ψ)α, is calculated directly using properties of the shape, that is, from the sphericity (ψ) and an exponent term (α). For prolate ellipsoids, α is 0.5, and for oblate ellipsoids, α is 1.0. In the case of a sphere (a = b = c, ψ = 1), Equation 9 reduces to the original form presented in Equation 7.
An approximation model for generalized ellipsoids was also developed and investigated. This approach calculates a shape-specific RC by computing the geometric mean (GM) of RCs calculated using the Gustafsson-Mínguez equation (Eq. 4) for spheres with radii equal to each axis dimension. For an ellipsoid with dimensions (a,b,c), the RC is approximated by first calculating RCs of spheres with radii a, b, and c (using Eq. 4) and then calculating the GM of RCa, RCb, and RCc (Eq. 10) to approximate the RC (RCa,b,c) of the ellipsoid. We refer to this as the RECOVER-GM model.
Eq. 10where RCa, RCb, and RCc are the mean RCs for spheres with radii a, b, and c, respectively. To benchmark the RECOVER-EM and -GM models (Eqs. 9 and 10), prolate ellipsoids (a:c ratios of 1:2, 1:4, 1:8, and 1:16) and oblate ellipsoids (a:c ratios of 2:1, 4:1, 8:1, and 16:1) were simulated in Python, and 3D Gaussian filters were applied in ImageJ to simulate RCs for a range of volumes and for a system with a spatial resolution measuring 18-mm FWHM. The simulated RC curves were compared with RC curves generated with the RECOVER-EM and -GM models. MRD% and absolute RC differences generated with the two models were compared with the simulated RCs within the RC range of 0.05 to 0.90. A conventional sphere-based assumption was included for reference, in which RCs were calculated using Equation 4 with the volume-equivalent spherical radius.
Resolution Measurements from NEMA IEC Phantoms
Seven NEMA IEC phantom experiments were performed for a range of PET and SPECT radionuclides and SBRs and were reconstructed with various reconstruction parameters. The NEMA IEC phantom with the standard 6 spherical inserts (inner diameters Ø = 10, 13, 17, 22, 28, and 37 mm) was used, and the SBR varied from 8:1 to no background. PET acquisitions included 18F and 68Ga on a Siemens Quadra system and 68Ga on a Biograph mCT. Reconstructions were performed using the clinical reconstruction protocol with resolution modeling (RM) and postreconstruction filtering (for 68Ga)—additional reconstructions without RM and no postfiltering (all-pass) were also performed. SPECT acquisitions included 99mTc (low-energy high-resolution collimator) and 177Lu (medium-energy low-penetration collimator) on a Siemens Intevo 6 system in body-contour mode. Data were reconstructed with CT-based attenuation and transmission-dependent scatter correction. The reconstructions were performed using in-house quantitative SPECT software using the ordered-subset expectation-maximization (OSEM) algorithm without RM. An additional 177Lu SPECT acquisition was acquired on a GE 870 DR system (medium-energy general-purpose collimator) and was reconstructed using OSEM (Xeleris4) with default vendor settings that included RM.
RCs were measured using a threshold-based VOI (Hermes Medical), using a variable threshold (%) on the reconstructed images to generate VOIs that best matched the known volumes of the phantom inserts. RCout was calculated from RCmeas by rearranging Equation 2 as follows:
Eq. 11 If RCout and the radius (R) of the sphere are known, the resolution (FWHM) can be calculated from a measured, simulated, or theoretical RCout by rearranging Equation 7: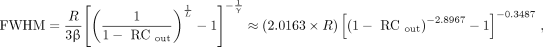
Eq. 12where V/SA is replaced by R/3 and RCout was calculated from RCmeas using Equation 11. The expression on the right incorporates the empirical fit parameters β, γ, and L, derived from the 3-PL (Eq. 7) fit to Equation 4 simulated RCs and has been further simplified. These fit parameters are discussed in more detail later in the text. It is worth noting that Equation 12 gets within an average of approximately 0.1% of the FWHM calculated by inverting Equation 4 using numerical root-finding methods to iteratively solve for σ. We refer to Equation 12 as the resolution equivalent recovery coefficient (RERC) equation because it calculates the spatial resolution (Gaussian FWHM) that is required to produce the measured RC, given the known radius and SBR (18). The RERC equation was used to calculate the resolution of each sphere in the NEMA IEC phantom reconstructed images.
DROs were generated for each phantom experiment by carefully segmenting the CT images of the physical IEC phantom. Spherical VOIs with known diameters were used to segment the spheres, whereas a relative percent threshold was used to segment the background compartment. The VOIs were then exported to ImageJ. A DRO was generated for each IEC phantom experiment to minimize coregistration errors between the reconstructed image and the DRO. MFAs were performed in Python, where the DROs were successively blurred with 3D Gaussian functions with FWHMs ranging from 1 to 20 mm in 0.01-mm increments. The global spatial resolution estimate was identified as the Gaussian FWHM that minimized the sum of squared differences between the DRO and the reconstructed image. The MFA spatial resolution estimates were compared with the RERC estimates.
A simulated test example was also performed to validate the RERC and MFA methodology. A DRO reflecting an 8.8:1 SBR was convolved with an 18-mm FWHM Gaussian (Supplemental Fig. 1; supplemental materials are available at http://jnm.snmjournals.org), and the RCs were measured; RCout was then calculated by correcting for spill-in from the background using Equation 11. The RERC equation (Eq. 12) and an equivalent form derived using the 2-PL equation fit (Eq. 6) were then used to estimate the effective spatial resolution in the spheres. An MFA was also conducted to validate the MFA methodology under ideal conditions. The spatial resolution estimates from each method were compared to assess the impact of the Equation 6 and 7 fits to theoretical RCs and to evaluate the RERC methodology against a conventional MFA under known resolution conditions.
Validation of the MIRD-RC Models for PVC
To investigate the utility of the RECOVER-EM and RECOVER-GM models for PVC, we used phantom data first presented by Mínguez et al. (11). Briefly, 9 spheres, 9 oblate ellipsoids (a:c ratio ≈ 4, ψ ≈ 0.70), and 9 prolate ellipsoids (c:a ratio ≈ 2, ψ ≈ 0.93) were filled with a known activity concentration of 99mTc and 177Lu; the 6 smallest spheres were part of the standard NEMA IEC phantom inserts (Ø = 10 to 37 mm), and the other 21 inserts were 3D-printed. The spheres and ellipsoids had the same volume but different surface areas. The phantom experiments did not include background activity. 99mTc acquisitions were performed using a Siemens Symbia Intevo Bold SPECT system with a low-energy high-resolution collimator, and the images were reconstructed using OSEM (Flash3D) with RM and with CT-based attenuation and window-based scatter corrections. 177Lu acquisitions were performed using a GE NM/CT 870 DR SPECT system with a medium-energy general-purpose collimator, and the images were reconstructed using OSEM (Xeleris4) with RM and with CT-based attenuation and window-based scatter corrections. In both cases, 24 iterations and 4 subsets were used, and a Gaussian filter of 8.4-mm FWHM was applied after reconstruction as per the clinical protocol. Mínguez et al. (11) has additional acquisition and reconstruction parameters. The signal rates per activity in each of the 27 inserts were measured using the same threshold method described previously and were converted to RCs using the system calibration factors (counts per second/MBq).
The RECOVER-EM model was used to calculate the average resolution for each insert shape (sphere, prolate, oblate) by rearranging Equation 9 for FWHM, and RECOVER-EM RC curves were generated and compared with the experimental data. A least-squares line-of-best-fit analysis showed that the resolution values extracted from each of the shapes was better parametrized using the generalized radius (ρ), defined as ρ = 3 × (V/SA) = ψR (8), compared with the volume-equivalent sphere radius (R). We then performed a PVC test using the 6 standard NEMA IEC phantom spheres (Ø = 10 to 37 mm) to generate a conventional EANM 2-PL RC curve (16) and a resolution model–based approach using the RECOVER-EM (Eq. 9) and RECOVER-GM (Eq. 10) models. The resolution-based PVC methodology is as follows: the resolution model is generated using the measured RCs (Eq. 12) from the 6 IEC phantom spheres in which a line of best fit using the least-squares method is fit to the resolution (FWHM) versus phantom sphere diameters (FWHM = m × diameter + b); the line of best fit is used in the RECOVER-EM and RECOVER-GM models, in which the generalized radius (ρ) of the object is used to determine the resolution (FWHM = m × 2ρ + b) applied in the RECOVER models; the resolution and a:c axis dimensions are used to derive RCout using the RECOVER-EM and -GM models (parameters SA and ψ for the RECOVER-EM model are calculated directly from the input a:c ratio); and the RC that is applied for PVC is calculated using Equation 5 (Cmeas,obj = 0 ∴ Ctrue,obj = Cmeas,obj/RCout). The RECOVER-EM model requires only 2 additional input parameters (a:c) to apply a shape-specific correction; the RECOVER-GM model requires 3 additional parameters (a,b,c) to apply a shape-specific correction; however, it should be noted that the RECOVER-GM model is generalizable to any ellipsoid.
RCs of the remaining 21 inserts (27 phantom inserts – 6 IEC phantom spheres) were normalized to a nominal ground truth activity concentration of 100 kBq/mL for the PVC test. Three PVC models—EANM RC curve (Eq. 3), RECOVER-EM, and RECOVER-GM—were each calibrated using the IEC phantom RCs and were used to perform PVC on the 21 remaining inserts: the 3 largest spheres, 9 prolate, and 9 oblate ellipsoids. The partial-volume corrected activities calculated using each model are reported.
RESULTS
A RC Model for Spheres
Figure 1A shows the theoretical RCout generated using Equation 4 for spherical volumes of 0.005–125 cm3 and simulated spatial resolutions of 1–19-mm FWHM, with the x-axis collapsed to (V/SA)/FWHM; EANM 2-PL (Eq. 6) and empirical 3-PL (Eq. 7) functions are fit to the RC data. The β, γ, and L parameters for the 3-PL function (Eq. 7) fit are 0.1653, 2.8679, and 0.3452, respectively. These parameter values should be used when implementing the RECOVER-EM model (Eq. 9) and the RERC equation (Eq. 12). The b1 and b2 parameters for the 2-PL function (Eq. 6) are 0.3353 and 1.6248, respectively. Figure 1B shows the absolute RC difference (RCtheoretical − RCmodel) of the 3-PL empirical model and the 2-PL model fits. For the range of RCs investigated (0.0005–0.9836), the MRD% between RCs predicted using our 3-PL empirical model and the EANM 2-PL model, compared with the theoretical RCs, were 0.32% and 15.3%, respectively. The mean absolute RC difference for our model (3-PL) and the 2-PL function compared with the theoretical RCs was 0.0003 (RCtheoretical − RC3-PL: maximum, 0.0006; minimum, −0.0007) and 0.0210 (RCtheoretical − RC2-PL: maximum, 0.0246; minimum, −0.0520), respectively.
(A) Simulated spill-out RCs using Equation 4 for volumes ranging from 0.005 to 125 cm3 and spatial resolutions range of 1–19-mm FWHM and EANM 2-PL (Eq. 6) and empirical 3-PL (Eq. 7) fits to data. (B) Absolute difference in RC values between 3-PL model fit and 2-PL fit compared with simulated RCs. Eq Diff = equation difference.
Extending the Model to Ellipsoids
Simulated RCs and RCs generated with the RECOVER-EM (Eq. 9) and RECOVER-GM (Eq. 10) models are shown in Figures 2 and 3. RC curves for prolate (1,1,2) and oblate (4,4,1) and (16,16,1) are presented as a function of (V/SA)/FWHM and [V/SA/FWHM]−1 in Figure 2. It is evident that for an RC greater than 0.7, the various RC curves collapse onto a single curve when presented as a function of (V/SA)/FWHM (Figs. 2A and 2C). The linear behavior of large volumes, also discussed previously (8,10,11), is evident when presented as a function of [V/SA/FWHM]−1 (Figs. 2B and 2D).
Simulated, RECOVER-EM (Eq. 9), and RECOVER-GM (Eq. 10) RC curves for prolate (1,1,2), oblate (4,4,1), and (16,16,1). RC curves shown as function of V/SA/FWHM (A and C) and [V/SA/FWHM]−1 (B and D). Linear behavior for large volumes relative to FWHM (low [V/SA/FWHM]−1 values) are marked by dotted line in (B and D).
Simulated, RECOVER-EM, and RECOVER-GM model RC curves as function of volume (cm3) for a spatial resolution of 18-mm FWHM. RECOVER-EM: prolate (A) and oblate (B). RECOVER-GM: prolate (C) and oblate (D). Prolate ellipsoids simulated with a:c ratios of 1:2, 1:4, 1:8, and 1:16, and oblate ellipsoids simulated with a:c ratios of 2:1, 4:1, 8:1, and 16:1.
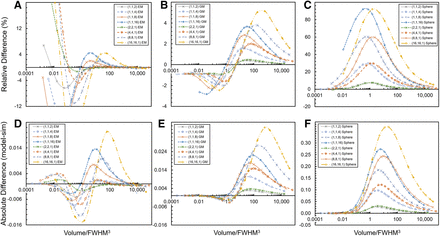
The mean, maximum, and minimum relative percent difference and absolute difference for all shapes investigated are shown in Table 1 and Supplemental Table 1, respectively. Figure 4 shows the relative percent (Figs. 4A–4C) and absolute (Figs. 4D–4F) difference curves of the RECOVER-EM and -GM models compared with simulated RCs. It is evident that the RECOVER-EM model reproduces the simulated RC values more accurately in the high V/FWHM3 range (RC > 0.6), whereas the RECOVER-GM model reproduces the simulated RC values more accurately in the low V/FWHM3 range (RC < 0.4). A conventional sphere-based correction calculated using Equation 4 (with the volume-equivalent spherical radius) is included for reference (Figs. 4C and 4F).
MRD% and Minimum Percent Difference (Min % diff) and Maximum Percent Difference (Max % diff) for RECOVER-EM and RECOVER-GM Models Compared with Simulations*
Relative difference curves compared with simulated (sim) RCs for RECOVER-EM (A), RECOVER-GM (B), and spherical assumption (Eq. 4) (C) and absolute difference curves for RECOVER-EM (D), RECOVER-GM (E), and spherical assumption (F).
Resolution Measurements from NEMA IEC Phantoms
Spatial resolution estimates obtained using an MFA and the RERC equation (Eq. 12) for a range of PET and SPECT radionuclides are shown in Table 2. Note that the RERC approach produces similar global (sphere average RERC) spatial resolution estimates to MFAs but with additional individual sphere measurements. Figure 5 shows spatial resolution measurements of 99mTc and 177Lu SPECT, and 68Ga and 18F PET, using the RERC equation and a conventional MFA.
Resolution Estimates Obtained Using MFA and RERC Equation for a Range of PET and SPECT Radionuclides
Spatial resolution estimates obtained using MFA and RERC method for 68Ga and 18F PET using clinical reconstruction protocols for Siemens Biograph Vision Quadra PET/CT scanner (A) and 99mTc and 177Lu SPECT, both without RM and postfiltering (B). Ave = average.
Spatial resolution estimates obtained using the RERC equation (Eq. 12), the EANM 2-PL function equivalent of the RERC equation, and from the MFA for the simulated test case are shown in Supplemental Table 2. Across the 6 phantom spheres, the 3-PL RERC model (Eq. 12) and the 2-PL equivalent function produced average spatial resolution estimates of 18 ± 0.1 and 20.7 ± 3.7 mm, respectively.
Validation of the MIRD-RC Models for PVC
Model-generated 99mTc RC curves for the 9 spheres, 9 oblate ellipsoids, 9 prolate ellipsoids, and the experimentally measured RCs are shown in Supplemental Figure 2. RCs greater than 0.7 are shown to lie on similar curves when plotted as V/SA versus RC (Supplemental Fig. 2A), consistent with previous findings (11). When the data are plotted as V versus RC (Supplemental Fig. 2C), the need for shape-specific corrections is highlighted. Figure 6 shows the PVC results for 99mTc and 177Lu for the 9 prolate and 9 oblate ellipsoid inserts. The MRD% results for the 99mTc and 177Lu PVC test are summarized in Table 3.
PVC results for 99mTc prolate (A), 99mTc oblate (B), 177Lu prolate (C), and 177Lu oblate (D) ellipsoid inserts. Dotted line indicates reference activity concentration of 100 kBq/mL.
MRD% of PVC Activity Concentrations Relative to Nominal Ground Truth Activity Concentration (100 kBq/mL) for 99mTc and 177Lu Inserts and Average RERC for Each Shape Using RECOVER-EM Model
DISCUSSION
The 3-PL function (Eq. 7) provides a better fit than the 2-PL function (Eq. 6) described in EANM guidance documents (16). The additional parameter in the 3-PL model enables an asymmetric function, unlike the symmetry imposed by the 2-PL model. Within the clinically relevant RC range, the 2-PL model’s largest RC difference from theoretical values was −0.0520, which would translate to a 38.3% error in the extracted RERC resolution. In contrast, the 3-PL model had a maximum RC difference of −0.0007, which would only translate to a 0.2% error in the extracted RERC. In addition to the 3-PL model providing more precise resolution estimates from measured RC data, we propose that a 3-PL function of the form shown in Equation 7, replacing V/SA*FWHM with V, like in Equation 3, could replace 2-PL functions for conventional RC curve approaches to PVC.
The RECOVER-EM and -GM models were developed in this work to address the need for shape-specific RC-based PVC. Generally, the RECOVER-EM model aligns closely with simulated RCs for RCs greater than 0.6, whereas the RECOVER-GM approximation improves accuracy in the low-RC range, which is critical for clinical applications, as errors in this range can lead to large uncertainties in the partial-volume corrected activity concentration. Additionally, minor absolute errors in mid to high RCs with RECOVER-GM (Fig. 4) do not propagate to significant errors when PVC is applied. Figures 2–4 illustrate the differences between the models, with RECOVER-GM showing stable accuracy in the low-RC range (relative difference, −1% to −2.5%) even as shape compactness decreases. For higher RCs, the RECOVER-GM model exhibits larger relative differences than does the RECOVER-EM model, evident in Figure 4. Both models show significant improvements over a conventional spherical assumption, reducing the MRD% by factors of approximately 4–21 (RECOVER-EM) and 8–20 (RECOVER-GM) and mean absolute error by factors of approximately 10–38 and 8–15, respectively.
Variability in individual sphere resolution estimates using the RERC method may arise from factors such as segmentation errors and phantom filling procedure errors, as well as systematic factors such as phantom orientation and volume-dependent convergence. Spatial resolution estimates obtained using MFA and RERC for various PET and SPECT radionuclides (Table 3) are comparable, and in most cases, MFA resolution lies between the minimum and maximum sphere resolution obtained with the RERC equation (Eq. 12). In the simulated test case, the RERC equation accurately estimated individual sphere resolutions with an average RERC similar to the MFA resolution, whereas the 2-PL fit failed to accurately characterize the applied 18-mm FWHM Gaussian filter (MFA, 18.0 mm; 3-PL, 18.0 ± 0.1 mm; 2-PL, 20.7 ± 3.7 mm). Given that the RERC approach estimates object resolution individually, it likely characterizes the global spatial resolution more accurately than MFA, which is skewed toward larger spheres (Ø = 28 and 37 mm) because of the limited contribution of smaller spheres in the MFA. This is highlighted in the volume-resolution plots in Figure 5B, which appear to show volume-dependent convergence in the 99mTc and 177Lu SPECT reconstructed images, with better resolution observed in the larger spheres. In the 177Lu images, there also seems to be better resolution in the spheres closer to the collimator. Investigating these effects under controlled conditions and at different SBRs could provide deeper insights into the method’s reliability and help distinguish systematic effects from random variability or segmentation errors. For example, different phantom configurations could be used to probe depth-dependent SPECT resolution (19). Future studies could also investigate a local matched-filter analysis alongside the RERC method for further validation.
The RECOVER-EM and -GM models showed significant improvement over the conventional EANM RC curve when applied to the ellipsoid phantom data (Fig. 6). The proposed RC-PVC methodology demonstrated the greatest improvement for the oblate ellipsoid phantoms, in which the EANM RC curve had a remaining mean absolute difference of 20.5% for 99mTc and 21.7% for 177Lu compared with nominal concentrations. This was reduced to 3.7% (RECOVER-EM) and 3.6% (RECOVER-GM) for 99mTc and 5.4% (EM) and 5.9% (GM) for 177Lu, translating to a quantification error reduction by factors ranging from approximately 1.3 to 5.7 (99mTc) and approximately 1.7 to 4.0 (177Lu). Unlike conventional RC curve PVC methods, resolution-based PVC inherently indicates the suitability of PVC for a given scenario, in which large variations in sphere resolution may indicate volume- or background-dependent convergence, suggesting PVC may be unreliable. Parameterizing the resolution model as a function of generalized radius was partly due to limited ellipsoid phantom data but is supported by observed behavior in experimental data (10,11). Further investigation into the convergence behavior with an expanded series of ellipsoidal phantoms is recommended.
These advancements in spatial resolution characterization have several practical applications. Improved spatial resolution characterization methods can enhance image harmonization across multicenter clinical trials to improve comparability and standardize absorbed dose calculations to better understand dose–response relationships within radiopharmaceutical therapy. The RERC method could be used to create a harmonization tool, similar to commercial software (e.g., Siemens EQ.PET (20)), which may facilitate centralized harmonization efforts using only site-provided RCs, avoiding the need for image data. The RERC method could also aid in reconstruction algorithm optimization by assessing the impact of reconstruction parameters (e.g., updates, postfiltering) on resolution (17,21). Additionally, the RERC method overcomes several limitations of conventional resolution measurements (22) by providing both location- and volume-dependent resolution assessments, which are lacking from MFA and line-based resolution measurements, respectively.
Like conventional RC curve approaches, the proposed RECOVER-EM and -GM models rely on accurate segmentation of VOIs for reliable PVC. Delineating tumors, especially on hybrid anatomic images, can be challenging because of low contrast between lesions and surrounding tissues, which may limit segmentation accuracy. Consequently, all PVC methods, including those presented here, require precise VOI definition for accurate corrections. The dependency on segmentation accuracy is inherent to RC-based PVC approaches and is also crucial for accurate absorbed dose assessments in target volumes and organs at risk. The RECOVER methodology shares the same input requirements as conventional RC curve methods for sphere-based corrections but eliminates the need for complex curve-fitting routines, facilitating a more seamless workflow and increased accessibility for routine clinical PVC. Additionally, the RECOVER-GM method facilitates shape-specific corrections when desired, with shape parameters extracted from VOIs using tools such as PyRadiomics (23). The RECOVER-GM model will serve as the basis of MIRDpvc, a MIRDsoft initiative in development that aims to make state-of-the-art RC-PVC methodology more accessible and to encourage the adoption of a standardized PVC methodology (24).
CONCLUSION
We have developed a MIRD model for estimating the RCs for spheres and ellipsoids. The RERC methodology for resolution characterization and PVC is undergoing further validation and may facilitate new approaches to quality assurance, algorithm optimization and harmonization, and shape-specific PVC. These results from simulations and experimental data support the need for shape-specific RC-PVC and suggest that RECOVER-GM is better suited for PVC because of its generalization to any ellipsoid and its stable accuracy in the low-RC range. Shape-specific corrections for simple region-based RC-PVC methods are crucial for improving the accuracy and accessibility of partial-volume corrected uptake measurements and absorbed dose estimates in radiopharmaceutical therapy. Additionally, the proposed models will help standardize PVC methodology, enabling reliable and comparable dosimetry results across institutions. Accordingly, the RERC equation and RECOVER-GM model are currently being implemented in the MIRDpvc software tool, a MIRDsoft initiative currently in development, which aims to make these advancements in RC-based PVC methodology accessible to the wider community.
DISCLOSURE
This research was funded in part through the NIH/NCI Cancer Center support grant P30 CA008748 and NIH U01 EB028234. C. Ross Schmidtlein was supported in part by the NIH/NCI R21 CA263876 and R01 EB032416. No other potential conflict of interest relevant to this article was reported.
ACKNOWLEDGEMENTS
This work was done in collaboration with the SNMMI MIRD committee: Vikram Adhikarla, Rachel M. Barbee, Wesley E. Bolch, Yuni K. Dewaraja, William D. Erwin, Valentina Ferri, Darrell R. Fisher, Roger W. Howell, Oleksandra V. Ivashchenko, Adam L. Kesner, Richard Laforest, Ruby Meredith, George Sgouros, Carlos F. Uribe, Pat B. Zanzonico (Chair).
Footnotes
Published online Jan. 30, 2025.
- © 2025 by the Society of Nuclear Medicine and Molecular Imaging.
REFERENCES
- Received for publication July 31, 2024.
- Accepted for publication December 16, 2024.
In this issue
Jump to section
Related Articles
Cited By...
- No citing articles found.