Abstract
This paper presents standardized methods for performing dose calculations for radiopharmaceuticals. Various steps in the process are outlined, with some specific examples given. Special models for calculating time–activity integrals (urinary bladder, intestines) are also reviewed. This article can be used as a template for designing and executing kinetic studies for calculating radiation dose estimates from animal or human data.
- image reconstruction
- radiation physics
- radiobiology/dosimetry
- radiopharmaceuticals
- clinical imaging
- radiation dosimetry
Currently, there is renewed interest in performing radiation dosimetry for radiopharmaceuticals, particularly in therapy applications. To have any new radiopharmaceutical approved by the U.S. Food and Drug Administration, whether for diagnostic or therapeutic applications, human radiation doses must be estimated. In 1999, Siegel et al. (1) published a guide for obtaining quantitative data for use in radiopharmaceutical dosimetry. The current article, and the companion article to it (2), updates that information with practical guidance and worked examples.
METHODS FOR BIOKINETIC DATA ANALYSIS
Whether the investigator has a series of data extrapolated from animals or a series of data from patient images, either planar or tomographic, one must integrate the human time–activity curve for each source region to get the area under the curve for all sources, which in each case is the number of disintegrations that occurred in that region. A kinetic model must be derived that can be used to estimate the number of disintegrations occurring in each significant source region in the body. In general, there are 3 levels of complexity that analysis can take: direct integration, least-squares analysis, and compartmental models.
Direct Integration
One can directly integrate under the actual measured values by several methods. This does not give much information about the biokinetic system, but it does allow calculation of the number of disintegrations rather easily. The most common method is the trapezoidal method, which uses linear interpolation between the measured data points and approximates the area under the time–activity curve as a series of trapezoids. An important concern with this method is calculation of the integrated area under the curve after the last datum. If activity is clearing slowly near the end of the dataset, a significant portion of the total decays may occur after the last time point and be represented by the area under the curve after that point. Several approaches may be used to estimate this area. The most conservative is to assume that activity is removed only by physical decay after the last point; another approach is to calculate the slope of the line using the last 2 or 3 points and assume that this slope continues until the retention curve crosses the time axis. No single approach is necessarily right or wrong—several approaches may be acceptable under different circumstances. It is generally preferable to overestimate the cumulated activity rather than to underestimate it, as long as the overestimation is not too severe. The important point is to calculate this area by an appropriate method and to clearly document what was done.
Least-Squares Analysis
An alternative to simple, direct integration of a dataset is to attempt to fit mathematic functions to the data; these functions then can be analytically integrated. The most common approach is to characterize a set of data by a series of exponential terms, as many biologic processes are well represented by this form, and exponential terms are easy to integrate. In general, the approach is to minimize the sum of the squared distance of the data points from the fitted curve. The curve will have the following form:
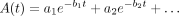 Eq. 1
Eq. 1
The fitting minimizes the sum of the squared differences between each point and the solution of the fitted curve at that point, taking the partial derivative of this expression with respect to each of the unknowns ai and bi and setting it equal to zero. Once the ideal estimates of ai and bi are obtained, the integral of A(t) from zero to infinity is simply…
 Eq. 2
Eq. 2
If the coefficients ai are in units of activity, this integral represents cumulated activity (the units of bi are time−1). If the coefficients give fractions of the administered activity, then the area represents the normalized cumulated activity (e.g., Bq-h/Bq).
Consider the dataset in Table 1. We will integrate it by the trapezoidal and least-squares methods (3).
Theoretic Dataset
Trapezoidal Method
Each interval is treated separately, and the parts are added, as shown in Table 2.
Trapezoidal Integration
Least-Squares Method
A computer fit of the data yielded the following fit (Fig. 1):

Sample biokinetic dataset, showing 2-exponential fit.
The cumulated activity for this system, integrating from zero to infinity, then is…
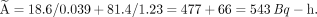
This does not agree well with the estimate from the trapezoidal method. The reason is that in that calculation, we did not estimate the area under the curve beyond 10 h. If we integrate the analytic expression only to 10 h, the answer is…
 This does agree well with the trapezoidal estimate. The appropriate calculation to apply to the trapezoidal case is that beyond the last data point, activity decreases with either the radioactive half-time or, if it can be estimated reliably, the half-time for the last phase of clearance. In this case, the second phase has a half-time of…
This does agree well with the trapezoidal estimate. The appropriate calculation to apply to the trapezoidal case is that beyond the last data point, activity decreases with either the radioactive half-time or, if it can be estimated reliably, the half-time for the last phase of clearance. In this case, the second phase has a half-time of…
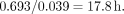
The area under the curve beyond 10 h, assuming that this rate continues, is…
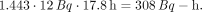
Adding this value to the previous estimate for the trapezoidal method yields 540 Bq-h, in excellent agreement with the estimate obtained by the least-squares method. Of course, the second half-time was obtained by the least-squares method. If these data were for, say, 131I, and if one did not feel that there was a good estimate of this (effective) half-time, the remaining area would have to be estimated as follows:

This estimate is an order of magnitude higher than the previous estimates and may be overly conservative. Many people, because of the possibility that another, slower, clearance phase might exist, will use this assumption even if a least-squares method has been used to fit the existing data. In this case, this highly conservative assumption may unrealistically increase the estimate of the normalized cumulated activity (Ã/A0) and thus the estimated dose to this and other organs. But if a slower component did exist, the assumption that the 17.8-h clearance rate continued beyond 10 h could have resulted in a considerable underestimation of the number of disintegrations.
Compartmental Models
The situation may arise that either quite a bit about the biologic system under investigation is available or more about how this system is working is desired to be known. In this case, one may describe the system as a group of compartments linked through transfer rate coefficients. Solving for à of the various compartments involves solving a system of coupled differential equations describing transfers of the tracer between compartments and elimination from the system. The solution to the time–activity curve for each compartment will usually be a sum of exponentials that are obtained not by least-squares fitting of each compartment separately but rather by varying the transfer rate coefficients between compartments until the data are well fit by the model. Computer programs such as SAAM II (The Epsilon Group; https://tegvirginia.com/software/saam-ii/), Stella (Isee Systems; www.iseesystems.com), PMOD (PMOD Technologies; https://www.pmod.com/web/), Simple (4), and others have been used for these purposes.
DOSIMETRIC METHODS
Basic Dose Calculations
A generic equation for the absorbed dose rate in an organ or tumor in which radioactivity is uniformly distributed is given by the following:
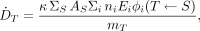 Eq. 3
where
Eq. 3
where  is the absorbed dose rate in the target region T (rad/h or Gy/s), AS is activity (μCi or MBq) in source region S, ni is the number of radiations with energy Ei emitted per nuclear transition, Ei is energy for the ith radiation emitted by the nuclide (MeV), ϕi (T←S) is the fraction of energy emitted that is absorbed in the target region T originating in source region S, mT is the mass of target region T (g or kg), and k is a proportionality constant (rad-g/μCi-h-MeV or Gy-kg/MBq-s-MeV).
is the absorbed dose rate in the target region T (rad/h or Gy/s), AS is activity (μCi or MBq) in source region S, ni is the number of radiations with energy Ei emitted per nuclear transition, Ei is energy for the ith radiation emitted by the nuclide (MeV), ϕi (T←S) is the fraction of energy emitted that is absorbed in the target region T originating in source region S, mT is the mass of target region T (g or kg), and k is a proportionality constant (rad-g/μCi-h-MeV or Gy-kg/MBq-s-MeV).
It is essential that the proportionality constant be properly calculated and applied for the unit system of choice. One may also apply radiation weighting factors (once called quality factors) to the result of this equation to calculate the equivalent dose rate. For many years, this issue was not important because nuclear medicine involved only β- and γ-emitters (for which radiation weighting factors are 1.0); the more recent introduction of some α-emitters makes this consideration important. The value recommended by the International Commission on Radiological Protection (ICRP) for the radiation weighting factor for α-emitters is 20, but this is believed to be too high for use in calculating doses from nuclear medicine therapy agents (5). Some radiobiologic evidence indicates that this value may be as low as 5 (6) or even 1 (7).
We are usually interested in an estimate of the total absorbed dose from an administration, rather than an initial dose rate. In Equation 3, the activity (nuclear transitions per unit time) causes the outcome of the equation to have a time dependence. To calculate cumulative dose, the time integral of the dose equation must be calculated. In most cases, the only term that has time dependence is activity; the integral is therefore just the product of all factors in the equation except for activity multiplied by the integral of the time–activity curve.
Regardless of the shape of the time–activity curve, its integral, however obtained, will have units of the number of total nuclear transitions (i.e., activity, which is transitions per unit time, multiplied by time). Therefore, the equation for cumulative dose would be given by the following:
 Eq. 4
where DT is the absorbed dose in target region T (rad or Gy) and NS is the number of disintegrations (cumulated activity) in source region S (μCi-h or MBq-s). NS is the total area under the time–activity curve, which may be due to contributions from one or more exponential terms, with different effective half-times.
Eq. 4
where DT is the absorbed dose in target region T (rad or Gy) and NS is the number of disintegrations (cumulated activity) in source region S (μCi-h or MBq-s). NS is the total area under the time–activity curve, which may be due to contributions from one or more exponential terms, with different effective half-times.
ANTHROPOMORPHIC PHANTOMS
The factors ϕ and mT in the equation above are determined using models of the human body referred to as phantoms. A very simple, and not very anthropomorphic, phantom is the International Commission on Radiation Units and Measurements reference sphere (8). For many decades, there was only one set of phantoms available for use in internal dosimetry: the Oak Ridge phantom series (3,9). These have now been replaced with image-derived, realistic phantoms (10) that are based on reference masses defined by the ICRP (Fig. 2) (11).
(A) Cristy–Eckerman stylized computational phantoms (8). (B) Realistic, voxel-based RADAR nonuniform rational B-splines phantoms.
SPECIAL CASES
The Dynamic Urinary Bladder
Developing the area under the curve for most organs requires the acquisition of several data points over the time of uptake and elimination of the radiopharmaceutical. In the case of the urinary bladder, however, except for very short lived nuclides for which no emptying of the bladder may occur during the decay of the nuclide, obtaining enough data points to characterize the complex filling and voiding pattern is not possible (Fig. 3).
Hypothetical urinary bladder time–activity curve, with and without periodic voiding.
An ingenious solution to the integration of this complicated curve was developed by Cloutier et al. (12) and is implemented in the OLINDA/EXM computer code (13):
 Eq. 5
Eq. 5
Here, the number of disintegrations, N, is given knowing the rate constants for clearance from the body, λ, and the (assumed regular) bladder voiding interval T. It should be noted, however, that empiric evidence suggests that, in reality, people urinate when their urinary bladders have filled to a particular volume, which varies among individuals (14), and not at constant time intervals.
The Gastrointestinal Tract
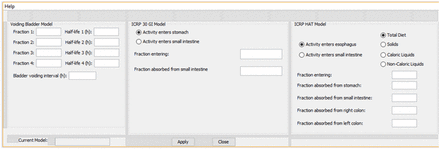
Quantification of activity in the stomach and intestines is also more difficult than in most body organs, because of the continuous movement of material through the system. The ICRP has developed 2 models (Fig. 4) that facilitate calculation of the activity in the stomach and intestines, given an input of the fraction of administered activity that enters at either the stomach or the small intestine (15,16). These models have also been implemented in the OLINDA/EXM software code (Fig. 5) (13).
ICRP 30 and ICRP 100 gastrointestinal tract models.
OLINDA/EXM data entry form for dynamic bladder and gastrointestinal models.
Remainder of Body
The remainder of the body is a special source organ that contains all the cumulated activity that is not assigned to any other source organ. It depends on which organs are not included in it. The challenge is that we do not have a dose factor (MIRD called these S values) for each of the numerous possibilities for the remainder of the body. Instead, we modify the total-body S factor to compute the S factor for the remainder of the body (Eq. 12 and Fig. 6) (13):
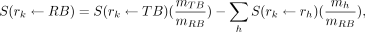 Eq. 6
where rh denotes the source organ with index h, rk denotes the target organ with index k, and RB and TB denote the remainder of the body and the total-body source organs, respectively. Recall that the S value is the mean absorbed dose in the target organ per disintegration in the source organ.
Eq. 6
where rh denotes the source organ with index h, rk denotes the target organ with index k, and RB and TB denote the remainder of the body and the total-body source organs, respectively. Recall that the S value is the mean absorbed dose in the target organ per disintegration in the source organ.
Remainder-of-body method. Since remainder of body depends on which source organs are identified, dose conversion factor must be computed for each situation. The fundamental concept is to apportion cumulated activity in each source organ into 2 parts. One part has the same cumulated activity density as remainder of body, which yields total body with uniform cumulated activity, and the second part of the source organ has the remaining cumulated activity.
Blood Data and the Archaic Quantity Dose to Blood
Blood data are relatively easy to gather and analyze but generally are difficult to use in internal dose calculations. Activity clears from the blood and is distributed into various organs. Later, some activity reenters the blood and is excreted. We are usually interested only in the dose to organs in the body; the dose to the blood itself is not of direct interest biologically. However, an early publication (19) suggested the use of dose to blood as a surrogate for the dose to the bone marrow in the safe administration of 131I in therapy. Blood is not a defined source or target region in any anthropomorphic phantom. Akabani (20) attempted to develop absorbed fractions for different-sized blood vessels, but this has not been implemented in any practical way. Because dose to blood is physiologically not meaningful, it should be abandoned in practical internal dose calculations. Very well developed models for the dose to the bone marrow are available (e.g., 21) and are implemented in the OLINDA/EXM computer code.
Patient-Individualized Target Organ Mass Corrections
It is common in cancer patients to encounter organs whose masses are notably different from those in the standard models, because of the disease or complications thereof. The reported dose using a standard model may be adjusted for mass, scaling of the electron, and photon dose contributions separately. For electrons, the scaling is as follows:
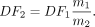 Eq. 7
Here, DF1 and DF2 are the dose factors appropriate for use with organ masses m1 and m2. For photons, the scaling is as follows:
Eq. 7
Here, DF1 and DF2 are the dose factors appropriate for use with organ masses m1 and m2. For photons, the scaling is as follows:
 Eq. 8
where phi (ϕ) is the absorbed fraction and Phi (Φ) is the specific absorbed fraction.
Eq. 8
where phi (ϕ) is the absorbed fraction and Phi (Φ) is the specific absorbed fraction.
To perform this calculation, one must isolate the emissions and frequencies for penetrating and nonpenetrating emissions, multiply them by these new absorbed fractions, and then recalculate the total dose by adding the 2 components together. The OLINDA/EXM code (13) performs this calculation automatically for the user, given entry of the new mass of the organ of interest. The correction for electrons assumes that all electron energy is absorbed in the source region, which is an approximation that is generally used in internal dose calculations. Newer absorbed fractions for electrons include explicit electron transport and possible losses at source region surfaces.
Total-Body Dose and Effective Dose
Although complete dose tables give doses to all defined target organs in the reference anthropomorphic phantoms, the 2 doses of the greatest interest have traditionally been those to the critical organ (i.e., the organ receiving the highest absorbed dose) and the total body. For most radiopharmaceuticals, however, the dose to the total body, which is the energy deposited in all target regions divided by the mass of the whole body, is of no biologic relevance. If one receives a uniform dose to all tissues of the body, this can predict biologic response, but for most radiopharmaceuticals this is not a useful quantity because the actual dose distribution is highly nonuniform by design and intention. Imagine, for example, an administration of 131I sodium iodide for which a large amount of β-energy is deposited in a 20-g thyroid gland. Dividing this same energy into 70,000 g of body tissue gives a vastly smaller dose number that has no clinical meaning. Instead of the uniform whole-body dose, the ICRP developed a quantity called effective dose, which gives a risk-based weighted average dose for diagnostic radiopharmaceuticals.
Assume for a given compound that the liver receives 0.53 mGy, the kidneys receive 0.37 mGy, the ovaries receive 0.19 mGy, the testes receive 0.07 mGy, the red marrow receives 0.42 mGy, the endosteal cells on bone surfaces receive 0.55 mGy, and the thyroid receives 0.05 mGy (3). Because all radiation weighting factors are 1.0, these absorbed doses can be directly converted to equivalent dose, that is, the absorbed radiation dose in grays times the radiation weighting factor (wR) (Table 3).
Theoretic Organ Doses
Strictly speaking, radiation weighting factors are dimensionless. Because Gy = 1 J/kg and 1 Gy × wR = 1 Sv, wR may be thought of as having units of Sv/Bq. The tissue weighting factor (wT) for the gonads may be applied to the higher of the values for the ovaries or testes. There is a little confusion on this point; ICRP 30 (22) used the higher of the two, whereas ICRP 53 (23,24) used the average of the two. To use the remainder weighting factor in the ICRP 30 system, one chooses the 5 organs that are not assigned an explicit weighting factor and that have the highest dose equivalents and assigns them each a weighting factor of 0.06 (although a different scheme was applied to the remainder organs in the ICRP 60 system). In our example, we have only 2 organs to consider. Assign each a factor of 0.06, and ignore the remaining weight of 0.18 (of 0.30). The doses delivered to breast and lung and the other organs could be calculated and summed, but they will probably be of limited importance. To calculate the effective dose equivalent (He), add up the weighted dose equivalents (Table 4).
Effective Dose Calculation
So we would conclude that the He for this compound is 0.17 mSv (0.017 rem, or 17 mrem). This suggests that if the whole body were uniformly irradiated to receive 0.17 mSv, the individual would incur the same additional risk (of fatal cancer or genetic defects) as from the combination of 0.53 mSv to the liver, 0.37 mSv to the kidneys, and so forth.
The same calculation can be performed using the tissue weighting factors from ICRP 60 (Table 5) (25). The ICRP, which defined the term effective dose, explicitly noted that in any given calculation, all weighting factors may not be used, and the sum of the weighting factors does not always equal 1.0.
Another Effective Dose Calculation
It is important to emphasize that effective dose must not be used to evaluate the short-term effects in situations involving radionuclide therapy. Effective dose is based on stochastic effects of radiation, whereas because the intended effect of a therapeutic administration is deterministic, effective dose must not be applied to specific individuals. The tissue weighting factors are defined for populations, not individuals, and should not be used to develop numeric estimates of risks to populations in the low dose ranges—for example, diagnostic radiology or nuclear medicine procedures—as noted by the Health Physics Society in 2012 (17).
THE NEED FOR PATIENT-INDIVIDUALIZED DOSIMETRY FOR THERAPEUTIC USES OF RADIOPHARMACEUTICALS
In 2008, Stabin (26) addressed all the main objections that physicians and others cite for not performing patient-individualized dosimetry for radiopharmaceutical therapy administration, as is done for every cancer patient receiving external-beam radiation, every day. The reasons addressed were that performing such calculations is difficult and expensive, requiring too much effort; that there are no standardized methods for performing individualized dose calculations and that methods vary significantly among institutions; that dose calculations performed to date have had poor success in predicting tissue response; and that with the level of difficulty involved, there must be some objective evidence that the use of radiation dose calculations provides a positive benefit that justifies extra effort and cost.
The current article thoroughly addresses the second point; all other points will not be reargued here. But the conclusion remains that “Treating all nuclear medicine patients with a single, uniform method of activity administration amounts to consciously choosing that these patients be treated with a lower standard of care than patients who receive radiation externally for cancer treatments.” (26).
Patient-individualized medicine is being practiced in almost all disciplines in the radiation sciences today except radiopharmaceutical therapy. In the 2008 article (26), Stabin argued that “The time has come for this reasonable paradigm shift in the practice of nuclear medicine.” It was true then, and it is still true now.
CONCLUSION
Standardized methods for the quantification of animal data or human image data to provide numeric estimates of radiation dose from the use of radiopharmaceuticals are well established. They are outlined, with many examples, in this article. Imaging methods are improving and will continue to improve. The methods outlined here are adequate to provide guidance on the design and execution of preclinical or clinical studies to establish the radiation dosimetry of any radiopharmaceutical for diagnostic or therapeutic use with almost any technology. Medical professionals have been reluctant to perform patient-individualized dose calculations for nuclear medicine therapy patients, with one of the arguments being that no standardized methods are available and reliable for dose calculations. This article provides all the current methods and models needed for standardized dose calculations. More advanced methods are also currently in some commercial software programs, using image fusion methods to provide 3-dimensional distributions of dose at the individual-voxel level and dose–volume histograms. Patient-individualized dosimetry for nuclear medicine therapy should become standard practice. The only people in modern medicine who do not receive patient-individualized dosimetry are nuclear medicine therapy patients. We generate dose estimates for adults and children receiving CT scans, for airline crews, for nuclear workers, and for nuclear medicine doctors and technologists, just not for nuclear medicine therapy patients. Not only is this resulting in suboptimal therapy for the patients, but when patients may need other therapies in the future, knowledge of previous therapy doses is essential to planning those treatments. It is time to change the historical practice of using a one-dose-fits-all approach to nuclear medicine therapy.
DISCLOSURE
No potential conflict of interest relevant to this article was reported.
Footnotes
Published online August 05, 2021.
- © 2022 by the Society of Nuclear Medicine and Molecular Imaging.
REFERENCES
- Received for publication February 1, 2021.
- Revision received May 5, 2021.