Abstract
A cylinder phantom positioned at a slightly oblique angle with respect to the z-axis of a PET scanner allows for fine sampling of the edge-spread function. We show how this technique can be used to measure the spatial resolution that can be expected with clinical PET protocols, potentially providing more relevant estimates than are typically obtained with established experimental procedures. Methods: A 20-cm-diameter water-filled cylinder phantom containing a uniform 18F solution was centrally positioned at a small angle with respect to the z-axis of a clinical PET/CT system. The oblique angle ensures that the phantom edge intersects the image matrix differently in different slices. Combining line profiles from multiple slices results in a composite profile with fine sampling. Spatial resolution was measured as the full width at half maximum (FWHM) by fitting a model to the finely sampled edge-spread functions in both radial and axial directions. The technique was validated by controlled modulation of image reconstruction parameters and by comparison with extended phantoms with fillable inserts. Separate experiments with uniform cylinders containing 18F, 11C, 13N, 68Ga, and 124I were used to further assess the proposed method. Results: Controlled adjustment of a gaussian postreconstruction filter was accurately reflected in the measured FWHM values. Recovery coefficients derived using the cylinder FWHM values agreed closely with recovery coefficients derived from physical phantoms over a range of insert-to-background ratios, phantom geometries, and reconstruction protocols. The effect of increasing positron energy was clearly reflected in the FWHM values measured with different isotopes. Conclusion: A method has been developed for measuring the spatial resolution that is achieved with clinical PET protocols, providing more relevant estimates than are typically obtained with established procedures. The proposed method requires no special equipment and is versatile, being capable of measuring resolution for different isotopes as well as for different reconstruction protocols. The new technique promises to aid standardization of PET data acquisition by allowing a more informed selection of reconstruction parameters.
The importance of uniform, high-quality imaging has been recognized as radiology strives for greater consistency and higher clinical value (1). Variations in image quality between different centers, and also between different scanners within the same institution, complicate image interpretation, particularly when comparing sequential studies. As radiology incorporates progressively more quantitative components, standardization of image generation is becoming yet more significant (2). Indeed, for research studies, particularly in a multicenter setting, variations in methodology have been identified as a major problem (3), one that may hinder potentially transformative developments such as artificial intelligence (4).
In PET, variations in image quality between scanner systems can be attributed to a variety of factors: differences in image statistical quality (5), the accuracy of corrections for scatter and attenuation (6), and artifacts (7), sometimes characteristic of the reconstruction algorithm (8). Another obvious consideration is spatial resolution. PET spatial resolution is typically dependent on the isotope of interest, the material in which the positrons annihilate, detector design, image reconstruction factors, location within the field of view, and direction of measurement. Conventional approaches for measuring spatial resolution involve point sources in air and reconstruction using unapodized filtered backprojection (9). Additional reconstructions involving alternative algorithms may also be used, and differences in resolution have been noted when images are reconstructed with the iterative algorithms typically used in clinical practice (10). Furthermore, clinical protocols usually include noise-reduction filters that significantly degrade spatial resolution compared with the limits of performance that are presented in manufacturer specifications. Although the effect of certain filters can be inferred, other common filters or reconstruction parameters are more ambiguous and their impact on spatial resolution may be unclear. It is therefore not straightforward to determine the spatial resolution of clinical PET images, and as a result, much variability exists between different centers, even for common protocols such as oncologic 18F-FDG imaging.
Efforts to encourage greater standardization of PET image quality and quantitative accuracy have recently been undertaken by several major organizations (11–13). These projects aim to make imaging protocols more uniform, and some have included initiatives to align spatial resolution across centers. Various experimental phantoms with fillable inserts of different sizes have been used (14). These phantoms do not measure spatial resolution directly but instead determine recovery coefficients, a parameter series that is closely related to spatial resolution. Using these phantoms, image reconstruction parameters can be optimized for individual scanners so as to produce recovery coefficients that best match a specified reference range (15). Phantom approaches of this sort have been validated for patient imaging (16) and have been shown to lead to greater consistency between diverse scanner systems (12).
As the PET community moves toward more consistent image quality, greater emphasis is being placed on the verification of spatial resolution. Professional societies (17) and institutional accreditation bodies (18) have introduced specific requirements for regular quality assurance of image spatial resolution. Although the limits of performance obtained using point sources (9) are important to measure at the time of system installation, these data bear little relation to the resolution that can be expected with clinical protocols, unless the protocol involves unapodized filtered backprojection. Furthermore, point-source experiments are difficult to perform as an ongoing test and are prone to error, particularly for measurement in the axial direction where sufficiently thin slices are not always feasible. A more practical and perhaps more useful alternative measures spatial resolution using a simple cylinder phantom (19,20) of the sort that is available at most sites. Cylinder phantoms are already widely used for routine quality assurance and could potentially be used in an expanded role, to assess not just scanner calibration accuracy and uniformity but also spatial resolution.
In this paper, we show how a standard uniform cylinder phantom, positioned at a slightly oblique angle with respect to the z-axis of the scanner, allows for accurate measurement of the spatial resolution achieved with clinical protocols. This method, which to our knowledge has not been previously used with PET, has major advantages over our earlier method (19) in that it enables finer sampling of the edge-spread function and allows measurement in the axial direction as well as the radial direction. It also has significant advantages in terms of ease of implementation, as it involves simple phantom preparation and data acquisition. The technique was validated by a series of tests including controlled adjustment of image reconstruction parameters and comparison of results obtained with different isotopes. In addition, we show how this technique can be used to predict recovery coefficients for extended phantoms with different geometries, contrast ratios, and reconstruction parameters. In this way, we aim to validate a novel method that can encourage greater standardization of PET images, hopefully contributing to improved quality and clinical value.
MATERIALS AND METHODS
Method Overview
We have previously proposed a method for measuring PET spatial resolution from the edges of a uniform cylinder phantom (19). Although this procedure worked well at our own institution, it did not transfer effectively to other sites. The problem was related to the need for higher spatial sampling than is typically used for clinical images. Specifically, the requirement for sites to alter reconstruction protocols so as to produce phantom images with 1-mm pixels, although not a major obstacle in theory, frequently proved to be problematic. Given that a specific aim of the method was that it should be capable of being implemented uniformly and easily across all centers, this requirement represented a significant limitation.
In light of this experience, we have developed a new phantom procedure that does not require sites to change their clinical reconstruction protocol in any way. Instead of being positioned in the conventional orientation, parallel to the longitudinal axis of the scanner, the cylinder phantom is positioned at a small angle, offset with respect to the z-axis (Fig. 1A). In this way, the edge of the cylinder intersects the image matrix at slightly different positions in each slice. By appropriately displacing and then combining line profiles from different slices, the edge response function can be measured with a sampling interval much finer than the pixel spacing of the original images. From these finely sampled, composite-edge profiles, the spatial resolution of the system can be determined by fitting an analytic function and measuring the full width at half maximum (FWHM). The FWHM is a well-established metric for characterizing spatial resolution that is meaningful and intuitive for imaging specialists and nonspecialists alike.
(A) Sagittal PET/CT image of obliquely positioned uniform cylinder phantom. Line profiles across edge of phantom are indicated in y- and z-directions. (B) These profiles across oblique phantom boundary are displaced with respect to each other. (C) From each profile, location of edge of cylinder was estimated. (D) Composite profile was formed by shifting original profiles to form new, finely sampled profile; continuous line is result of fitting analytic function to composite edge profile.
Cylinder Phantom Acquisition
The proposed method is compatible with cylinder phantoms of various dimensions, but to make the technique more readily transferrable, we used a 20-cm-diameter cylinder of the sort widely used in the PET community. Unlike the earlier method (19), the exact diameter of the phantom is not required for the analysis; therefore, cylinders from various manufacturers, even cylinders with slightly different dimensions, are compatible. The phantom that was used had an interior diameter of 20 cm, an internal length of 20 cm, and a volume of 6,283 mL, confirmed by measurements performed with an accurate balance. The walls of the phantom were made of polyethylene (−70 Hounsfield units on 120-kVp CT), had no internal indentations, and were 5 mm thick. The phantom was completely filled with water, containing a positron-emitting radiopharmaceutical in aqueous solution. In the standard implementation, approximately 111 MBq (3 mCi) of 18F were used, although alternative isotopes were also used and will be described subsequently. The phantom was positioned on the scanner bed in the usual orientation, with the long axis of the cylinder parallel to the z-axis of the scanner. The positioning lasers of the scanner were used to ensure that the phantom was accurately centered within the transverse field of view, and a spacer was then inserted so as to raise one end of the phantom by approximately 2 cm (Fig. 1A). A stack of paper served as the spacer in these experiments, although other readily available materials could be used. The exact thickness of the spacer was not critical and did not have to be measured because it was accounted for during data analysis. With the phantom secured in place, PET/CT data were acquired using a standard clinical protocol. To capture the axial component of spatial resolution as well as the radial component, the entire phantom was included in the field of view, using multiple bed positions as necessary. Unless otherwise stated, data were acquired on a Biograph mCT (Siemens Medical Solutions) using a clinical whole-body protocol. The CT parameters included 120 kVp, 80 mAs reference, 0.8 pitch, 0.5-s rotation time, 4.0-mm slice thickness, and 3.3-mm slice increment. The PET acquisition parameters included no septa, time of flight, 435- to 650-keV energy window, 4.1-ns coincidence time window, 21.8-cm axial field of view, and 9-cm bed overlap. The PET scan duration was increased to 30 min per bed position so as to collect at least 1 × 109 true counts, but the clinical acquisition and reconstruction protocols were not otherwise altered. Images were reconstructed using 2 different protocols (Table 1), one optimized for low noise (protocol A) and the other for high resolution (protocol B).
PET Image Reconstruction Parameters for Protocols A and B
Cylinder Phantom Analysis
Phantom image analysis consisted of the following steps: measuring line profiles through the phantom, estimating the edge of the phantom in each profile, combining multiple profiles to form a finely sampled composite profile, and fitting an analytic model to the composite profile, thereby estimating spatial resolution. This procedure was performed separately for both the radial and the axial components by taking line profiles in transverse planes and in the axial direction, respectively (Fig. 1A). Although automated analysis software has been developed, all results in this paper were generated using readily available software (Microsoft Excel, 2013) for profile manipulation and model fitting.
Line Profiles
For both the radial and the axial directions, multiple line profiles were measured (n = 5 in the current implementation), each separated by approximately 1 cm. The exact separation depended on the voxel dimensions. For the radial analysis, this meant taking profiles in a transverse slice (y-direction) through the center of the phantom and 4 other slices offset in the z-direction by ±1 cm and ±2 cm. For the axial analysis, this meant taking line profiles along the z-axis and 4 other profiles offset in the y-direction by ±1 cm and ±2 cm. The image-derived line profiles are denoted by pi(s), where i indicates the different profiles (i = 1,…n) and s is the distance in the y- and z-directions for radial and axial profiles, respectively. Although each line profile crossed an edge of the phantom at 2 locations, for simplicity we consider transitions across only one edge.
Edge Determination
Each line profile was analyzed to estimate the location of the edge of the radioactive portion of the phantom. The angle of the phantom meant that this edge occurred at slightly different locations along each of the different line profiles. The mean uptake in the cylinder images (m) was first determined by averaging voxels within the phantom (m expected to be around 1.0 for images calibrated in SUV). For each line profile i = 1,...n, linear interpolation was used to estimate the location of the phantom edge by determining the position (si) where the profile equals m/2, that is, pi(si) = m/2. To make for a more robust implementation, si was plotted as a function of the perpendicular distance between profiles (Fig. 1C). A linear fit to these data was performed, and the estimates of the phantom edge in each profile (si) were replaced by the appropriate points on the straight line fit.
Composite Edge Profile
A composite profile was formed by shifting the original profiles and then combining them to form a new, finely sampled profile. The shifting was necessary to account for the fact that different edge profiles across an oblique phantom boundary are displaced with respect to each other (Fig. 1B). Using 2-dimensional matrix notation, Pi refers to a given line profile i, shifted such that it is centered around its own edge: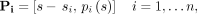
Eq. 1where s is the 1-dimensional vector of spatial samples and pi(s) is the corresponding 1-dimensional vector of edge profile measurements. Figure 1D shows how this process aligns profiles measured at different locations. A composite profile C combines these profiles into a single matrix:
Eq. 2In comparison to the original profiles, the composite profile C contains much finer spatial samples (first column) with corresponding edge profile intensities (second column).
Model Fit
Under the assumption that spatial resolution can be modeled as a gaussian point-spread function, the edge-spread function is given by the integral of the PSF:
Eq. 3where ESF is the edge-spread function, PSF is the point-spread function, A is a scale factor that allows for data with arbitrary magnitude (e.g., units of SUV or activity concentration), μ is the center of the gaussian function, and σ is the SD of the gaussian point-spread function and is related to the FWHM by
Eq. 4The analytic function ESF(s) was fitted to the discrete image-derived composite profile C using weighted least-squares minimization, where A, μ, and σ were simultaneously optimized. During the fit, each data point was weighted according to its inverse, based on the approximation that this is similar to weighting inversely proportional to the variance. The FWHM was computed from the value of σ that gave the best fit.
Method Validation
Adjustment of Image Reconstruction and Other Parameters
18F cylinder data were acquired on 3 separate occasions and reconstructed according to the protocols shown in Table 1. In addition, the behavior of our proposed method with respect to controlled adjustment of image spatial resolution was investigated. To do this, images were reconstructed using protocol B, as well as 7 additional image sets reconstructed using the same protocol but with the application of postreconstruction 3-dimensional gaussian filters with FWHM ranging from 2 to 8 mm. The effect of adjusting iterations was also investigated. To do this, images were reconstructed using both protocol A and protocol B, along with additional reconstructions using different numbers of iterations from 1 to 10. Apart from the number of iterations, all other parameters remained unchanged. These experiments involved phantoms displaced by 20 mm, but to assess the effect of the tilt angle, additional data were acquired with the phantom displaced by 10, 15, 20, 25, and 30 mm.
Comparison with Extended Phantoms
A series of experiments was performed to assess the extent to which FWHM measurements determined from the cylinder were applicable to other more extended radionuclide distributions. Both the American College of Radiology (ACR) PET phantom and the National Electrical Manufacturers Association (NEMA) image quality (IQ) phantom were used. Ten replicate preparations of the ACR phantom were performed at a 2.5-to-1 insert-to-background ratio. Five preparations of the NEMA IQ phantom were performed, each with a different sphere-to-background ratio: 2-, 4-, 6-, 8-, and 10-to-1. Data were acquired on a Biograph mCT at a single bed position, collecting at least 200 × 106 true counts. Images were reconstructed with the parameters shown in Table 1. The maximum voxel within generous volumes of interest over each phantom insert was used to determine recovery coefficients according to the following definition:
Eq. 5where Cinsert is the image-derived maximum voxel in the insert and Cbackground is the mean voxel value in a background region. Ainsert/Abackgound is the insert-to-background activity concentration ratio, determined using an accurate dilution technique.
FWHM values measured using the cylinder were used to estimate recovery coefficients that might be expected for the ACR PET and NEMA IQ phantoms. Idealized digital representations of the 2 physical phantoms were convolved with gaussian filters, equivalent to the FWHM values measured with the cylinder. These smoothed digital reference objects (DROs) were then used to predict recovery coefficients that would be expected with these phantoms and reconstruction protocols. Specifically, the DRO consisted of 0.25 × 0.25 × 0.25 mm voxels. Cylindric and spheric inserts were generated with dimensions equal to the dimensions of the ACR (8, 12, 16, and 25 mm) and NEMA IQ (10, 13, 17, 22, 28, and 37 mm) phantoms. Insert-to-background ratios were assigned so as to match the physical phantom experiments. The walls of the phantom inserts were simulated as shells 1.5 mm thick (ACR) and 1.0 mm thick (NEMA IQ) with no activity. The DROs were smoothed using a gaussian filter with the FWHM set to match the measurements obtained with the cylinder. A 3-dimensional gaussian filter was used for the spheric inserts of the NEMA phantom, whereas a 2-dimensional gaussian filter was used for the ACR phantom because the inserts are cylindric, with a relatively long extent in the axial direction. Because the cylinder method measures only the radial and axial components of resolution, the tangential component was approximated by the radial measurement for the purpose of these calculations. After smoothing of the DRO, recovery coefficients were determined by applying a volume of interest at the center of the insert, with dimensions equal to the voxel size of the physical phantom images. In this way, recovery coefficients were estimated on the basis of the cylinder measurements of spatial resolution and compared with conventional measures of recovery determined with the ACR and NEMA IQ phantoms.
Comparison of Different Isotopes
The applicability of the cylinder method to different positron-emitting isotopes was assessed. A series of experiments was performed with the cylinder phantom filled with aqueous solutions of 18F, 11C, 13N, 124I, and a solid 68Ge/68Ga phantom of the same dimensions. 124I data were corrected for prompt γ-coincidences using the Biograph mCT standard software, and all images were reconstructed using the protocols described previously (Table 1). Apart from the different isotopes involved in each experiment, all data were acquired under identical conditions. The intention was to assess the extent to which the cylinder-based FWHM measurements reflected the known differences in positron range associated with the different isotopes.
Multicenter Application
Applicability of the cylinder technique to multiple sites with different scanner systems was assessed. Five different sites contributed phantom data for 7 scanners, including systems from Siemens Medical Solutions, GE Healthcare, and Philips Healthcare. Sites used their own cylinder phantoms and acquired 18F image data according to written instructions. Each site reconstructed images using their usual clinical protocol for whole-body 18F-FDG oncology studies, and all images were submitted for central analysis.
RESULTS
Adjustment of Image Reconstruction and Other Parameters
Table 2 shows spatial resolution measured using the proposed cylinder method. For protocol A, the measured FWHM was 7.07 ± 0.10 mm (radial) and 7.82 ± 0.12 mm (axial). For protocol B, the measured FWHM was 5.53 ± 0.19 mm (radial) and 5.78 ± 0.09 mm (axial). Radial analysis used the cylinder edge farthest from the bed by default. Analysis of the edge nearest the bed resulted in a relative increase in FWHM by 4.8% for protocol A and 0.6% for protocol B. Repeated measurements at a fixed 20-mm phantom displacement indicated a coefficient of variation of 1.4% (protocol A, radial direction). Corresponding data acquired with the phantom at different angles ranging from 2° to 8° had a coefficient of variation of 1.6%. Figure 2A shows radial FWHM measurements (FWHMmeasured) for images reconstructed with gaussian filters of various sizes (FWHMfilter). The parameters on both x- and y-axes have been squared under the assumption that FWHMmeasured and FWHMfilter are related by
Eq. 6FWHMintrinsic denotes the spatial resolution without application of any filter. Figure 2A shows a linear fit to the data such that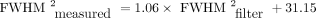 
. The intercept indicates a FWHMintrinsic of 5.58 mm (√31.15), which is consistent with the data in Table 2. The slope of the fit was close to unity, confirming that the cylinder measurements are consistent with Equation 6 and respond as expected to controlled adjustment of image spatial resolution. Figure 2B shows radial FWHM measurements for cylinder images reconstructed with different numbers of iterations. Increasing the number of iterations improved the spatial resolution, although the magnitude of the changes was small. From 2 iterations to 10 iterations, FWHM decreased by 5% for protocol A and 4% for protocol B.
Biograph mCT Spatial Resolution Measured Using Cylinder Technique
Radial FWHM measured using cylinder method as function of increasing gaussian filtering (A) and iterations (B). In A, measured results and postreconstruction gaussian filtering are both shown to power of 2 to illustrate expected behavior. In B, FWHM derived using cylinder method is shown as function of increasing iterations (21 subsets) for 2 different reconstruction protocols.
Comparison with Extended Phantoms
Figure 3 shows recovery coefficients for the ACR and NEMA IQ phantoms as a function of insert diameter. Figure 3A shows data for the ACR phantom, reconstructed using protocol A. The different-colored datasets correspond to 10 repeated experiments at a 2.5-to-1 insert-to-background ratio. The solid green line was derived from a DRO with the same 2.5-to-1 insert-to-background ratio after smoothing with a 2-dimensional gaussian filter. This gaussian had a FWHM of [7.07, 7.07 mm], corresponding to the spatial resolution measured with the cylinder method (Table 2). Figure 3B shows data for the NEMA IQ phantom, also reconstructed using protocol A. In this case, the different-colored data points correspond to different sphere-to-background ratios. Note the similarity of the recovery coefficients obtained with these very different sphere-to-background ratios. The green line was derived from the DRO (6-to-1 sphere-to-background ratio shown) after smoothing with a 3-dimensional gaussian filter, with a FWHM of [7.07, 7.07, 7.82 mm]. Figure 3C shows data similar to Figure 3B, but in this case the images were reconstructed using protocol B. For this reconstruction protocol, the filter applied to the DRO had a FWHM of [5.53, 5.53, 5.78 mm] (Table 2). Note the close agreement between the recovery data derived from the cylinder measurements (continuous green lines) and the experimental data from the physical phantoms. These data indicate that the cylinder resolution measurements are consistent with conventional measures of resolution recovery.
Recovery coefficients for ACR PET phantom (A) and NEMA IQ phantom (B and C). A and B were reconstructed with protocol A, whereas C was reconstructed with protocol B. In A, discrete data points correspond to 10 replicate phantom experiments with 2.5-to-1 insert-to-background ratio. In B and C, discrete data points correspond to 5 different experiments with sphere-to-background ratios indicated in legend. Continuous green lines denote recovery coefficients derived from appropriate DRO, smoothed with 3-dimensional gaussian filter with FWHM values of [7.07, 7.07, 0 mm] (A), [7.07, 7.07, 7.82 mm] (B), and [5.53, 5.53, 5.78 mm] (C).
Comparison of Different Isotopes
Figure 4 shows radial FWHM measured using the cylinder method for 5 different isotopes. The data are shown as a function of the average positron energy of the isotope (21). For isotopes that emit positrons of different energies, the most energetic positron was used for presentation. The expected trend toward increasing FWHM with increasing positron energy is clearly reflected in the cylinder measurements.
Radial FWHM measured using cylinder method for 5 different isotopes: 18F, 11C, 13N, 68Ga, and 124I. Data are presented as function of average energy of most energetic positron. Data corresponding to 2 different reconstruction protocols are shown. Continuous lines are polynomial fits to these data.
Multicenter Application
Figure 5 shows radial and axial FWHM measured with the 18F-FDG whole-body protocols of 7 different clinical scanners. In general, adherence to the phantom protocol was good, although in one case, insufficient axial coverage meant that only radial resolution could be measured. No 2 scanners used identical reconstruction parameters, and some variation in spatial resolution was noted. Sites 3 and 6 had substantially better spatial resolution than the wider group, most likely because of the use of image reconstruction with point-spread function modeling (resolution recovery). The remaining systems did not use point-spread function modeling and had broadly comparable spatial resolution, at least in the radial direction (mean, 6.9 ± 0.4 mm). Slightly poorer resolution was noted in the axial direction, particularly for systems 4–6. These scanner systems had detector crystals with a longer extent in the axial direction than in the tangential direction.
FWHM measured using cylinder method for 7 PET/CT systems at 5 different sites. Data correspond to 18F-FDG oncology protocols used with each system. Radial and axial components of spatial resolution are shown.
DISCUSSION
A method has been developed for measuring PET spatial resolution using a standard uniform cylinder phantom positioned at an oblique angle relative to the scanner axis. The method reflects the resolution that is achieved with clinical protocols, rather than the limits of performance under idealized conditions. As such, it can be used to compare different clinical protocols, potentially allowing for a more informed selection of image reconstruction parameters. The method is particularly amenable to widespread deployment because it involves a simple, readily available phantom. Significantly, it does not require user adjustment of image reconstruction parameters. These practical advantages mean the method can be readily adopted at different sites, potentially providing a way of satisfying the requirements of regulatory bodies regarding spatial resolution assessment. More generally, the hope is that the method will contribute to greater standardization of image quality by providing metrics that can be readily compared between centers.
Reliable methods for assessing image quality are badly needed, particularly in multicenter settings. Many sites that are capable of acquiring high-quality clinical data struggle to perform phantom experiments without dedicated physics support. Phantoms involving fillable compartments are notoriously prone to experimental error, and it is often unclear whether an abnormal phantom study indicates a genuine scanner problem or simply a phantom preparation error. In contrast, uniform cylinders can be easily prepared, and few sites have difficulty acquiring such images. A potential application of the cylinder method might involve use in conjunction with more realistic phantoms, rather than as a replacement. Images of the cylinder phantom can be acquired regularly as part of routine quality assurance, whereas images of more elaborate phantoms with fillable compartments need be acquired less frequently, perhaps only as part of periodic physics inspections.
Although the proposed method has not been previously applied in PET, similar approaches have been used in CT (22,23). The PET application was supported by several tests, including controlled adjustment of image reconstruction parameters. Figure 2A shows that the new method accurately reflected changes in image spatial resolution due to controlled adjustment of gaussian filtration. The method also reflected improvements in spatial resolution with increasing iterations (Fig. 2B). Some differences were noted between the results of the cylinder method and previously published measures of spatial resolution using point sources. For the mCT, the radial FWHM for a point source positioned at a distance equal to the radius of the cylinder (10 cm) has been measured as 5.2 ± 0.0 mm (24) and 5.48 ± 0.05 mm (local site measurements). The radial FWHM derived from the cylinder reconstructed with protocol B was 5.53 ± 0.19 mm. In the axial direction, point-source measurements were 4.4 ± 0.1 mm (24) and 4.11 ± 0.05 mm (local site measurements) at a radial distance of 1 cm and 5.9 ± 0.1 mm (24) and 5.49 ± 0.12 mm (local site measurements) at a radial distance of 10 cm. In comparison, the cylinder method resulted in an axial FWHM of 5.78 ± 0.09 mm. The use of different reconstruction algorithms likely contributes to the observed differences: Fourier rebinning with filtered backprojection in the case of the point sources and fully 3-dimensional iterative reconstruction in the case of the cylinder. A more direct comparison was not possible because the cylinder method performs poorly in conjunction with filtered backprojection because of negative pixels close to the edge of the cylinder that are not accommodated by the current analytic model. Although the discrepancies between the 2 methods were not great, we emphasize that the cylinder method is intended to characterize clinical protocols rather than measure the performance limits of a particular system.
Figure 3 provides further evidence that the cylinder-based FWHM measurements reflect the spatial resolution that can be expected with more complex emission distributions. Recovery coefficients determined by smoothing a DRO according to FWHM values derived with the cylinder were consistent with conventional measures of recovery. Good agreement was observed for 2 different phantom geometries and 2 reconstruction protocols, over a range of different sphere-to-background ratios. The greatest discrepancy was observed for the largest sphere in Figure 3C, where the NEMA IQ phantom images show artificially high recovery, greater than 100%. This positive bias is due to the maximum voxel being used in conjunction with unfiltered, noisy images and is not a limitation of the cylinder method. The fillable phantom inserts were located 5.7 cm (NEMA IQ) and 6.5 cm (ACR PET) from the center of the field of view, whereas the cylinder measurements were made at a 10-cm radial distance. As such, the cylinder measurements are not strictly equivalent to the extended phantom situation, although the small distances and their locations close to the center of the field of view mean the differences in resolution are relatively small.
Further support for the method was provided by experiments involving different isotopes. A trend toward increasing FWHM with increasing positron energy was clear (Fig. 4). Although not unexpected, such measurements are typically hard to perform with conventional techniques, and these data add support for the new method. Figure 5 confirms that the cylinder method has been successfully implemented across multiple centers, and there is considerable variation in spatial resolution between the clinical 18F-FDG oncology protocols at these sites. Axial resolution could not be calculated from the data provided by one scanner system (Fig. 5, system 7) because of an unexpectedly long cylinder phantom that was not anticipated in the version of the phantom instructions that was given to the site.
Other limitations should also be mentioned, including the fact that the cylinder method allows for measurement in only a limited number of directions and locations. With the current implementation, no measurement is possible in the tangential direction, and measurement in the radial direction is possible only at a distance equal to the radius of the cylinder, 10 cm in this case. The cylinder could potentially be displaced within the field of view, allowing resolution measurement at different radial distances, but the assumption of a gaussian point-spread function may break down at greater radial positions because of parallax errors. Alternatively, cylinders of different dimensions can be used, but a strength of the current implementation is that 20-cm-diameter cylinders are ubiquitous across the PET community. The walls of these phantoms are typically around 5 mm thick and are expected to be sufficient to absorb most of the positrons involved in the current experiments. Phantoms with thicker walls may be required for isotopes that emit higher-energy positrons. Another consideration is the application of the method to images reconstructed with point-spread function modeling. As shown in our multicenter evaluation, many sites use image reconstruction with point-spread function modeling as part of their clinical routine. Unfortunately, these algorithms give rise to unwanted Gibbs-like artifacts at the edge of the cylinder (8). In our experience, the model fitting analysis was not particularly sensitive to these edge artifacts. The results shown in Figure 5 were obtained with the conventional analysis described previously, but the method could potentially be optimized to better accommodate point-spread function reconstruction. Although further work is needed to confirm the validity of the method in this situation, the oblique cylinder approach may prove useful.
CONCLUSION
A method has been developed for measuring the spatial resolution that is achieved with clinical PET protocols, providing more relevant estimates than are typically obtained with established procedures. The proposed method requires no special equipment and is versatile, being capable of measuring resolution for different isotopes as well as for different reconstruction protocols. The new technique promises to aid standardization of PET data acquisition by allowing a more informed selection of reconstruction parameters.
DISCLOSURE
This work was partially funded by grants from the National Institutes of Health (HHSN268201500021C and U01CA140204). No other potential conflict of interest relevant to this article was reported.
Acknowledgments
We thank all who contributed data for this project, including Ronald Boellaard, Lance Burrell, Roberto Maass-Moreno, and Larry MacDonald. In addition, we gratefully acknowledge helpful discussions with Ray Muzic, the SNMMI Clinical Trials Network Scanner Validation Committee, and the RSNA Quantitative Image Biomarker Alliance, FDG PET Biomarker Committee.
Footnotes
Published online Jun. 14, 2018.
- © 2018 by the Society of Nuclear Medicine and Molecular Imaging.
REFERENCES
- Received for publication February 7, 2018.
- Accepted for publication May 8, 2018.
Jump to section
Related Articles
Cited By...
- No citing articles found.