TO THE EDITOR:
I have read with interest the article of Sciacca et al. (1) reporting on a comparison of H215O and 1-11C-acetate for quantification of myocardial blood flow with PET. The aim of this study, to contribute to the validation of 1-11C-acetate as a quantitative flow tracer in myocardial PET, is certainly important. However, the article exhibits methodologic problems concerning tracer kinetic modeling as well as correction of partial- volume effects.
The authors assume the rate of tissue clearance to be equal to perfusion, F (Fig. 1; Eqs. 1 and 2 (1)). This assumption is not justified: It is known from animal data (2) that within approximately 15 s after passage of a very short intraarterially injected bolus, tracer concentration drops to an approximately constant plateau of about 2- to 3-min duration (the initial drop corresponding to the finite first-pass extraction). Tissue clearance occurs only after this plateau phase and is numerically an order of magnitude smaller than F. Therefore, postulating a clearance rate equal to F seems inconsistent with the actual behavior of acetate, and parameter estimation bias can be expected. It would actually be less problematic to neglect tissue clearance altogether during the first 3 min. It should be noted, however, that restricting data evaluation to this time range leads to substantial loss of statistical accuracy of the perfusion estimates in comparison with using longer fitting intervals. I believe, therefore, that a 1-compartment model without parameter constraints (i.e., setting K1 to zero and allowing for arbitrary clearance rates in Eqs. 1 and 2 (1)) would be a more adequate model. Such a model has the particular advantage of being able to fit the data over much longer time intervals (3,4).
Furthermore, I consider the described method for recovery correction to be questionable. Essentially, the FMM (which can be identified with the recovery coefficients if fractional blood volume is neglected) are adjusted in such a way that the flow values derived with H215O and 1-11C-acetate coincide if the individually adapted FMM are used. The good agreement of the perfusion values is, therefore, no proof of adequacy of the recovery correction method. Rather, the derived FMM empirically correct for all other sources of errors, such as model configuration and assumption of a constant extraction fraction. This conclusion is substantiated as follows. The general solution of Equations 1–3 (1) can be written as:
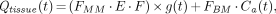 where E is the unidirectional extraction fraction, g(t) describes the shape of the tissue signal, FBM includes both spillover of counts from blood in the adjacent left ventricular cavity and counts from the fractional blood volume within the tissue region of interest, and Ca(t) is the tracer concentration in arterial blood. The amplitude of g(t) is given by:
where E is the unidirectional extraction fraction, g(t) describes the shape of the tissue signal, FBM includes both spillover of counts from blood in the adjacent left ventricular cavity and counts from the fractional blood volume within the tissue region of interest, and Ca(t) is the tracer concentration in arterial blood. The amplitude of g(t) is given by:
 Eq. 1
This amplitude is an easily identifiable parameter, but as long as arbitrary tissue clearance is allowed for (no influence of F on g(t)), it is impossible to identify the individual factors contributing to A. Even under the assumptions used by Sciacca et al. (1) (i.e., clearance equal to flow) it is still impossible to differentiate between FMM and E.
Eq. 1
This amplitude is an easily identifiable parameter, but as long as arbitrary tissue clearance is allowed for (no influence of F on g(t)), it is impossible to identify the individual factors contributing to A. Even under the assumptions used by Sciacca et al. (1) (i.e., clearance equal to flow) it is still impossible to differentiate between FMM and E.
Because Sciacca et al. (1) found relatively large discrepancies in the flow estimates obtained with H215O and 1-11C-acetate when using fixed values for E and FMM, they describe a procedure for improving the recovery correction, which essentially is equivalent to solving Equation 1 for FMM using the flow value determined in the H215O investigation for F. Correlating these individual adapted FMM to echocardiographic findings is then performed to enable individual recovery correction. Thus, agreement of flow values derived with 1-11C-acetate and H215O is enforced by the method.
Two other questions come immediately to mind in this context. Why did the authors not use the individual FMM that have been apparently derived from the corresponding H215O scans? How do the FMM derived by the authors’ method compare with those obtained from the H215O scans?
In conclusion, I think that the data of Sciacca et al. (1) make a valuable contribution to the ongoing efforts to validate 1-11C-acetate as a quantitative flow tracer, but the methods chosen to evaluate the acetate investigations seem to be inadequate. A modification of the model configuration, in combination with an implicit recovery correction as proposed, for instance, by Hutchins et al. (5), seems to be desirable.
References
REPLY:
Dr. van den Hoff raises several issues regarding our article (1), which showed that myocardial perfusion at rest can be measured quantitatively with 1-11C-acetate.
The first issue that Dr. van den Hoff raises pertains to the fact that we set the rate of tissue clearance to be equal to perfusion, F (Fig. 1 (1)). Despite Dr. van den Hoff’s assertions to the contrary, the observation that tissue–tracer activity plateaus for 2–3 min after initial extraction does not invalidate the model structure. In fact, the model depicted in Figure 1 (1) ensures that, as the input tracer activity level falls toward zero, total tissue activity will remain nearly constant. This is a consequence of the fact that the tracer cannot leave the metabolically trapped pool even as tracer activity levels fall toward zero both in arterial blood and in the freely exchangeable pool.
The underlying question is whether modeling the egress from the system to be equal to blood flow, F, is justified. It should be noted that net tissue clearance after the plateau phase that is less than what would be expected, based on perfusion, does not address the question because egress is only from the freely exchangeable pool, which contains only a small fraction of the total tissue–tracer activity. The equivalence of the clearance rate with the rate constant exiting the system is only true for a 1-compartment model. One way to address the question of how reasonable it is to model the egress as being equal to F is by examining the influence of the exit rate constant on estimates of perfusion. This can be accomplished by decreasing the rate constant to a small fraction of F or even to zero. When the rate constant is set to zero, there is a mean underestimation of blood flow of 34% among the group of healthy volunteers (range, 19%–47%). This contrasts with no significant difference in blood flow estimates with 1-11C-acetate and H215O using the published model structure (1).
The second issue Dr. van den Hoff raises regards our method for computing the recovery coefficient, FMM. Unfortunately, Dr. van den Hoff has overlooked the basis of the jackknife procedure and the point that the model as configured produced accurate blood flow estimates. In essence, the jackknife procedure allows one to perform an independent experiment for each subject in which the data from all other subjects are used as calibration, including control subjects for whom the adjustment was unnecessary. Although it is theoretically possible that extraction, as well as FMM (which cannot be determined independently from each other), could be altered in hypertrophy, there is no experimental evidence that this in fact is the case. The fact that the methodology is empiric does not invalidate its accuracy. The incorporation of FMM into other models has been previously proposed and validated (2–4).
Dr. van den Hoff raises additional concerns including the use of fitting data beyond 3 min to improve statistical accuracy and the use of FMM from the H215O scans as an alternative to the jackknife procedure. Use of data beyond 3 min would require correction for egress of metabolites (predominantly 11CO2), which would require additional analysis and, optimally, sampling from an arterial catheter. We wanted to develop a simpler approach obviating these steps. Using FMM from the H215O scans defeats the purpose of the study, which was to determine whether myocardial perfusion as well as myocardial oxygen consumption could be measured without resorting to additional tracers. It may be of interest, however, to note that the FMM from the jackknife procedure and from H215O scans correlated significantly (P = 0.01) and that the regression line had a slope of 0.86, which did not differ significantly from unity.
It should be remembered that all mathematic models are merely approximations that greatly simplify the system under study. In the context of PET, the primary objective of modeling is to find a structure that can be used to obtain parameter estimates that accurately reflect underlying biologic processes. The model that we proposed appears to be useful for allowing estimates of myocardial perfusion using 1-11C-acetate.






