Abstract
The high-resolution research tomograph (HRRT) is a dedicated human brain PET scanner. At present, iterative reconstruction methods are preferred for reconstructing HRRT studies. However, these iterative reconstruction algorithms show bias in short-duration frames. New algorithms such as the shifted Poisson ordered-subsets expectation maximization (SP-OSEM) and ordered-subsets weighted least squares (OSWLS) showed promising results in bias reduction, compared with the recommended ordinary Poisson OSEM (OP-OSEM). The goal of this study was to evaluate quantitative accuracy of these iterative reconstruction algorithms, compared with 3-dimensional filtered backprojection (3D-FBP). Methods: The 3 above-mentioned 3D iterative reconstruction methods were implemented for the HRRT. To evaluate the various 3D iterative reconstruction techniques quantitatively, several phantom studies and a human brain study (n = 5) were performed. Results: OSWLS showed a low and almost linearly increasing coefficient of variation (SD over average activity concentration), with decreasing noise-equivalent count rates. In decay studies, OSWLS showed good agreement with the 3D-FBP gray matter (GM)–to–white matter (WM) contrast ratio (<4%), and OP-OSEM and SP-OSEM showed agreement within 6% and 7%, respectively. For various frame durations, both SP-OSEM and OP-OSEM showed the fewest errors in GM-to-WM contrast ratios, varying 75% between different noise-equivalent count rates; this variability was much higher for other iterative methods (>92%). 3D-FBP showed the least variability (34%). Visually, OSWLS hardly showed any artifacts in parametric images and showed good agreement with 3D-FBP data for parametric images, especially in the case of reference-tissue kinetic methods (slope, 1.02; Pearson correlation coefficient, 0.99). Conclusion: OP-OSEM, SP-OSEM, and OSWLS showed good performance for phantom studies. In addition, OSWLS showed better results for parametric analysis of clinical studies and is therefore recommended for quantitative HRRT brain PET studies.
The high-resolution research tomograph (HRRT; CTI/Siemens) is a dedicated human brain PET scanner using high spatial resolution combined with high sensitivity (1,2). The scanner has 8 detector heads that are arranged in an octagon. Because of this geometry, gaps are present between the detector heads, leading to missing data. This is one of the main reasons that iterative reconstruction algorithms, which do not require these missing data to be estimated, are preferred for HRRT reconstructions (3). A 3-dimensional (3D) attenuation and normalization weighted ordered-subsets expectation maximization (ANW-OSEM) reconstruction method showed considerable bias for a homogeneous phantom (4). Therefore, a 3D ordinary Poisson OSEM (OP-OSEM) reconstruction method was implemented that showed considerably less bias, especially when randoms were estimated by the variance reduction on a randoms (VRR) algorithm (5). However, bias was still encountered for short-duration (5–60 s) frames (6,7). These frames suffer from low statistics, with high random fractions and scatter events, requiring an iterative reconstruction method without nonnegativity constraint. However, this constraint is needed in some iterative reconstruction algorithms to enable proper convergence. The nonnegativity constraint causes bias in short-duration frames.
Recently, we implemented a 3D filtered backprojection (3D-FBP) algorithm optimized for the HRRT (8) to validate new iterative reconstruction techniques. Missing data were estimated by gap-filling strategies, which will be described in more detail later in this article. 3D-FBP showed a higher precision when used in combination with the VRR algorithm (9).
Yavuz and Fessler (10) showed that shifted Poisson OSEM (SP-OSEM) reconstruction, compared with OP-OSEM reconstruction, reduced bias and provided better precision. Boellaard et al. (11) showed that an ordered-subsets weighted least-squares (OSWLS) reconstruction algorithm was a promising candidate for 3D brain PET studies performed on the HR+ scanner (CTI/Siemens), demonstrating lower variance and bias. Least-squares (LS) reconstruction does not apply a nonnegativity constraint on a sinogram level and may therefore show performance similar to that exhibited by FBP. Moreover, LS poses several other advantages over FBP. First, by applying attenuation correction as weights during LS reconstruction (i.e., weighted LS) (12), images have a better signal-to-noise ratio when obtained with LS than with FBP. Second, weighted LS does not require the correction for missing plane data in segments other than segment 0 (oblique lines of responses) or due to gaps between the detector heads (8). As a consequence, OSWLS might be a good alternative to 3D-FBP reconstructions. Therefore, implementation of these algorithms in the attempt to further reduce bias and improve signal-to-noise ratio in HRRT studies is of interest.
The purpose of the present study was to evaluate the above-mentioned 3D iterative reconstruction techniques for the HRRT in terms of quantitative accuracy under clinically relevant conditions and to assess whether and to what extent these algorithms suffer from bias as a function of noise-equivalent counts (NECs) (13). Results were compared with in-house–developed analytic 3D-FBP. Several phantom studies and a human brain study using 11C-flumazenil (n = 5) were performed to evaluate the performance of the various 3D reconstruction algorithms. To our knowledge, this study was the first to assess all of these 3D reconstruction methods in terms of quantitative accuracy for the HRRT on human brain studies.
MATERIALS AND METHODS
Reconstruction Algorithms
All implementations of the reconstruction algorithms were developed in-house. At the time of writing, commercial implementations exist for only OP-OSEM and ANW-OSEM, as provided by the manufacturer of the scanner.
OSEM
3D-OSEM is an iterative reconstruction method based on the maximum-likelihood principle and expectation maximization algorithm (14). It can be accelerated by using ordered subsets (15). Recently, the reconstruction code has been further optimized (16) by using a rotated projector, symmetries in image and projection space, and a vector-processor instruction set. Pseudo-true coincidences (t) can be corrected for scattered coincidences (s), attenuation (A), and normalization (N), an algorithm called ANW-OSEM, which is described mathematically as follows (4,17):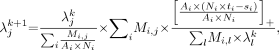 Eq. 1where λj is the value for image voxel j, Mi,j is the system matrix element for voxel j and sinogram element I, and […]+ denotes that all negative values are truncated to zero.
Eq. 1where λj is the value for image voxel j, Mi,j is the system matrix element for voxel j and sinogram element I, and […]+ denotes that all negative values are truncated to zero.
To avoid bias, an alternative approach, the current default OP-OSEM (4,18,19) scheme, was attempted, reconstructing raw prompt coincidences (p) and including all correction terms (as well as correcting for delayed coincidences (d)) in the iteration: Eq. 2
Eq. 2
To our knowledge, no SP-OSEM (18) has been implemented for the HRRT. Therefore, a 3D-SP-OSEM algorithm was implemented to study its effects on quantitative accuracy as follows (17,20): Eq. 3
Eq. 3
Further improvements were expected by using the VRR algorithm (5), which estimates expected randoms (vi) from measured delayed coincidences (9). The mathematic formulae are the same, except that vi is used instead of di, and the trues (ti) are calculated by pi − vi.
LS
LS can also be applied to the expectation maximization algorithm and accelerated using ordered subsets (OSLS) (12): Eq. 4
Eq. 4
OSLS can also be weighted by attenuation (OSWLS) and is written mathematically as: Eq. 5
Eq. 5
Again, in the latter method the pseudo-trues (ti) are calculated by pi − vi. To speed up convergence, starting images were initiated with a 2D-FBP image estimate of segment 0 data smoothed with a gaussian kernel of 5.7 mm in full width at half maximum (21).
3D-FBP
3D-FBP requires all missing data to be estimated before the 3D backprojection step. As previously reported (8), it is recommended to estimate the missing data caused by the scanner geometry using the constrained Fourier space method, which iteratively estimates these missing sinogram data by applying constraints in the Fourier domain (22). Additional missing (oblique planes) data were estimated as for 3D reprojection (23). The sinogram data were filtered using a Colsher filter (24) (cutoff at the Nyquist frequency), without additional smoothing. 3D-FBP should be used in combination with the VRR algorithm to improve precision (9). A detailed description of 3D-FBP for the HRRT has been described previously (8).
Phantoms and Studies
For calibration of the various reconstruction techniques, a homogeneous phantom of 20-cm diameter was used and filled with an 18F-FDG solution of 8 kBq/mL. In addition, this phantom was used with two 5-cm diameter and 20-cm-long inserts and filled with 18F-FDG solutions of 36 and 3 kBq/mL. The background compartment was filled with a solution of 8 kBq/mL. A 3D anthropomorphic human brain phantom (Hoffman phantom; Data Spectrum) (25) was used to compare realistic activity-concentration distributions in clinical situations. The phantom was filled with an 11C solution of 66 kBq/mL for a decay or linearity study or with an 18F-FDG solution of 50 kBq/mL to study the effects of NECs on reconstructed activity concentrations for various frame durations. For all phantom studies, an emission list-mode scan of 1 h was performed. List-mode scans of the homogeneous phantom were histogrammed in multiple frames with different durations (i.e., 5, 10, 30, 60, 300, 1,800, and 3,600 s). The list-mode scan of the Hoffman phantom was histogrammed in 300-s frames (11C decay experiment) or in multiple replicates (frames) with different durations (18F-FDG experiment): 20 frames of 5, 10, 30, and 60 s; 12 frames of 300 s; and 1 frame of 1,800 and 3,600 s. Transmission scans were performed after activity had decayed to background level.
Dynamic human 11C-flumazenil studies were used for clinical evaluation. In 5 healthy volunteers, a 60.5-min list-mode scan was acquired immediately after administration of 11C-flumazenil (363 ± 42 MBq). Each emission scan was histogrammed in 17 time frames with variable frame lengths (1 × 30, 4 × 15, 4 × 60, 2 × 150, 2 × 300, and 4 × 600 s). Before emission scanning and tracer administration, a 6-min transmission scan was performed. During emission scanning, continuous online arterial blood sampling was performed (26). At set times (5, 10, 15, 20, 30, 40, and 60 min after injection), continuous blood sampling was interrupted to collect manual blood samples. These manual sample data were used for calibrating the (online) blood sampler, for measuring plasma or whole-blood ratios, and for determining metabolite fractions (27). The metabolite-corrected arterial plasma time–activity curve was used as an input function for kinetic analysis. A structural T1-weighted MR image was acquired on a 1.5-T scanner (SONATA; Siemens Medical Solutions) used for region-of-interest (ROI) definitions. The medical ethics committee of the VU University medical center had approved the study, and the subjects had given written informed consent.
Reconstructions
All studies were normalized and corrected for scatter, randoms, attenuation, decay, and dead time. Emission scans were reconstructed using the various 3D iterative reconstruction techniques mentioned above. To assess convergence of all algorithms, the 10- and 3,600-s frames of the inserts phantom experiment and the 3,600-s frame of the 18F-FDG Hoffman phantom experiment were reconstructed with an increasing number of iterations (up to 30) and 16 subsets. The human brain study was reconstructed with different numbers of iterations but with a smaller range, to investigate the effects on dynamic human brain studies. All other experiments were analyzed at the optimal number of iterations as found with the convergence studies (as will be shown later in this article). In addition, all studies were reconstructed using the 3D-FBP algorithm (8), which was used as a reference for iterative reconstructions.
Parametric Analysis of Human Brain Study
Parametric images were generated using a basis-function-method implementation of a plasma-input single-tissue-compartment model (28,29) providing volume of distribution (VT) and delivery (K1) images. Furthermore, reference-tissue parametric analysis was performed using receptor parametric mapping with the pons as the reference region providing relative delivery (R1) and binding potential (BPND) images. Receptor parametric mapping is a basis-function-method implementation of the simplified reference-tissue model (30). These parametric methods were applied to assess the effects of different reconstruction strategies on the (overall) accuracy of kinetic analyses of PET data. Parametric images were generated using PPET (31).
Data Analysis
ROI Definition
For the homogeneous phantom study without inserts, a circular ROI was positioned in the center of the phantom, ranging over 38 planes and staying away from the edges by least 3 mm (volume, ∼1 L). For the phantom with 2 inserts, 3 ROIs were positioned in the background and within the inserts, ranging over 100 planes and staying away from the edges by at least 6 mm (volume, ∼1.3 L and ∼60 mL, respectively). For the Hoffman phantom, two 3D ROIs were identified manually (i.e., gray matter [GM; volume, 43.4 mL] and white matter [WM; volume, 37.2 mL] regions) to study bias in the GM and WM regions and the contrast between GM and WM.
For the human brain study, ROIs were defined using a GM and WM segmentation of the coregistered structural MRI scan to derive GM and WM subregions of 15 different manually defined ROIs, that is, the pons (reference region) and left and right regions of the thalamus, frontal lobe, temporal lobe, parietal lobe, occipital lobe, caudate, and putamen. For all regions, GM data were used, except for the pons, for which all data were used. Coregistration of the MR image was performed using VINCI (Max Planck Institute for Neurologic Research). GM or WM segmentation was performed using Statistical Parametric Mapping (SPM) (version 5; Wellcome Department of Cognitive Neurology, University College London). All ROIs were drawn manually using DISPLAY (Montreal Neurologic Institute). These ROIs were projected onto the parametric images to derive regional average pharmacokinetic parameters.
Assessment of Quantitative Accuracy
To study the various 3D iterative reconstruction techniques quantitatively, all images were compared with those using 3D-FBP, except for the images from the homogeneous phantom studies, which were normalized by dividing the reconstructed activity concentration by the true activity concentration. True activity concentrations were derived by measuring three 0.5-mL samples in a calibrated well counter. Coefficient of variation (COV; percentage) was calculated as the ratio of SD of the reconstructed activity concentration over all replicates to the observed average activity concentration. The average activity concentration was calculated as the average over all replicates.
The Hoffman phantom data were normalized to the measured activity concentration per region using the 3D-FBP image with the highest scan statistics. This procedure was followed because the slabs separating the compartments of the Hoffman phantom are about the same size as the scanner resolution and slice thickness, resulting in a variable partial-volume effect. Consequently, shifting the Hoffman phantom axially by half the detector width will result in a different image. Therefore, normalization to true activity concentration was not accurate.
True kinetic parameters were not known for the human brain study. Therefore, data were normalized by dividing them by the data obtained by 3D-FBP reconstructions. Consequently, only the relative difference in activity concentration with respect to those seen in the data obtained with 3D-FBP can be evaluated.
RESULTS
Convergence of Different Algorithms
Figure 1 shows convergence rates of various iterative reconstruction algorithms for the homogeneous phantom with hot and cold inserts at low (10 s) and high (3,600 s) NECs. All reconstruction algorithms had converged using 10, 16, 7, and 16 iterations for ANW-OSEM, OP-OSEM, OSWLS, and SP-OSEM, respectively. At low NEC, ANW-OSEM showed a bias of 29% for the hot and of 370% for the cold inserts. All other iterative reconstruction algorithms showed bias (21%−47%) for cold regions after convergence, but hardly any bias (<2%) for the hot insert. 3D-FBP showed a bias of −24% for the cold and of 7% for the hot inserts. At high NEC, all reconstruction algorithms showed only limited bias after convergence (∼5% for hot, ∼−10% for cold inserts). For cold regions, however, OSWLS hardly showed any bias (<3%) after convergence was reached.
Homogeneous phantom with inserts. Effects of increasing number of iterations of various reconstruction algorithms on cold insert with low (10 s) and high (3,600 s) NECs and on hot insert with low and high NECs. Note that OP-OSEM and SP-OSEM overlap.
Figure 2 shows bias versus COV for various iterative reconstruction algorithms in the case of the homogeneous phantom with hot and cold inserts at low (10 s) and high (3,600 s) NECs. After convergence (at a minimal or constant bias level), increasing the number of iterations increased COV at high NECs and increased both bias and COV at low NECs.
Homogeneous phantom with inserts. Effects of increasing number of iterations of various reconstruction algorithms on bias and COV in background and cold and hot inserts with low (10 s) and high (3,600 s) NECs. Arrows indicate suggested optimal number of iterations for various iterative reconstruction algorithms.
Convergence rates of various iterative reconstruction algorithms for the Hoffman phantom are shown in Supplemental Figure 1 (supplemental materials are available online only at http://jnm.snmjournals.org). Every reconstruction algorithm converged within 16 iterations to an acceptable GM-to-WM contrast ratio (comparable or better than that of 3D-FBP). The numbers of iterations required to obtain a resolution similar to 3D-FBP were equal to those seen in the inserts phantom study, that is, consistent with the numbers of iterations described above. All reconstruction algorithms showed hardly any bias (<1%) in GM and WM after convergence.
Homogeneous Phantom: Varying NECs
Figure 3 shows results obtained from the homogeneous phantom study without inserts. ANW-OSEM showed a large bias in reconstructed activity concentration, amounting to 66%−96% for short frame durations (5–60 s) or low NECs. OSWLS decreased this effect to 2%−19%. SP-OSEM showed bias of 0%−9% for these frames. Similarly, OP-OSEM showed only 0%−8% bias. 3D-FBP showed almost no bias (<2%) for all NEC or frame durations tested (5–3,600 s), but showed high COV (4.4·102%−1.5·103%) and SD (32–110 kBq/mL) for short-duration (5–60 s) frames. OSWLS showed the least, almost linear, increase in COV (1.3·102%−2.2·102%) with decreasing NECs (shorter frames).
Results of various reconstruction methods for homogeneous phantom: a reconstruction over true activity concentration at different NECs (A), with corresponding COV (B) and SD (C). Note that OP-OSEM and SP-OSEM overlap.
Homogeneous Phantom with Hot and Cold Inserts: Varying NECs
Background activity concentrations showed trends similar to those seen in Figure 3A for all reconstruction algorithms. The hot and cold inserts showed trends similar to those shown later for the Hoffman phantom in Figures 4A and 4B. However, all reconstruction algorithms overestimated the activity concentration of the hot insert by 5% at high NECs (300–3,600 s). 3D-FBP underestimated the activity concentration of the cold insert by 14%−19% at high NECs.
True activity concentration for various reconstructions of Hoffman phantom at different NECs (randoms fraction, ∼17.6%) for GM (A), WM (B), and GM-to-WM contrast ratio (C). Note that OP-OSEM and SP-OSEM overlap. Error bars indicate SD.
Hoffman Phantom: Varying NECs by Varying Frame Durations
All reconstruction algorithms showed no bias (<1%) in activity concentration distribution at high frame lengths (1,800 and 3,600 s; NEC > 3.6·108 counts). In Figure 4, results obtained for the brain phantom (18F-FDG experiment) are shown for all other frame durations (NEC). Performance of all iterative reconstructions depends on NEC (i.e., on frame length). Both OP-OSEM and SP-OSEM showed less bias in activity concentration than did other iterative methods. However, they still showed differences in activity concentration distribution as a function of NEC, with a 75% change in the GM-to-WM contrast ratio between long- and short-duration frames (P < 0.001). This is similar for most iterative methods with changes of 92% (OSWLS, P < 0.001) up to 105% (ANW-OSEM, P < 0.001). In all cases 3D-FBP provided the most accurate results, independent of the underlying noise level (with a maximum GM-to-WM contrast ratio error of 9%, which was not statistically significant; P > 0.5, except 30 s [P > 0.05]). However, 3D-FBP showed a large SD of up to 41% in GM-to-WM contrast ratio at low NEC, whereas iterative reconstruction methods showed less SD at low NECs (<10%).
Hoffman Phantom: Decay Study
Supplemental Figure 2 shows results obtained from the 11C-decay study. Most reconstruction methods had a constant GM-to-WM contrast ratio with decreasing NECs (between 8% and 10% maximum error in the GM-to-WM contrast ratio), except for ANW-OSEM, which showed a considerable change of 20% in the GM-to-WM contrast ratio. OSWLS (0%−4% difference), OP-OSEM (1%−6% difference), and SP-OSEM (3%−7% difference) showed good agreement with the first observed 3D-FBP GM-to-WM contrast ratio (2.34).
Clinical Example
For a single patient, time–activity curves reconstructed with various techniques are shown in Supplemental Figure 3. ANW-OSEM showed a bias of 10%−61% in GM, 24%−109% in WM, and 26%−100% in the pons for short-duration frames (15–60 s). Other iterative reconstruction techniques reduced bias in the GM, WM, and pons to within 3.9%, 15%, and 11%, respectively. OSWLS showed the best correspondence with the 3D-FBP pons time–activity curve (<8%). Axial parametric images are shown in Figure 5. Images of 3D-FBP are noisy, especially for K1 parametric data (and for R1 data; data not shown). Therefore, no good comparison could be made between 3D-FBP and 3D iterative reconstruction techniques for K1 and R1. Visually, ANW-OSEM, compared with the other reconstruction methods, showed a clear underestimation in BPND. OSWLS showed the fewest artifacts. Correlation between several parametric analyses are summarized in Tables 1 and 2. All results are compared with 3D-FBP parametric data. VT (Table 1) showed a slight positive bias for ANW-OSEM with respect to 3D-FBP (slope with intercept fixed at origin, 1.03), whereas other iterative reconstruction methods showed a slight negative bias (slope with fixed intercept at origin, 0.92–0.93). Using more than the recommended number of iterations did not show significant improvement (P > 0.05), whereas a lower number of iterations showed poorer performance (P < 0.05). For BPND (Table 2), ANW-OSEM showed a considerable negative bias with respect to 3D-FBP (slope with intercept fixed at origin, 0.48) and low correlation (Pearson correlation coefficient [r] = 0.91). Both OP-OSEM and SP-OSEM showed less bias with respect to 3D-FBP (slope with fixed intercept, 1.12–1.14) and a higher correlation (r = 0.96). OSWLS showed the best correspondence with 3D-FBP (slope with intercept fixed at origin, 1.02) and highest correlation (r = 0.99). Using a higher-than-recommended number of iterations for OSWLS showed only a slight improvement relative to 3D-FBP (slope with fixed intercept, 1.00; r = 0.98, P < 0.001).
Parametric VT, K1, and BPND images for human 11C-flumazenil study. Each column represents a different reconstruction method. BFM = basis function method; RPM = receptor parametric mapping.
Human 11C-Flumazenil Brain Study: Parametric VT
Human 11C-Flumazenil Brain Study: Parametric BPND
DISCUSSION
Convergence
A GM-to-WM contrast ratio comparable to the one for 3D-FBP was found as an acceptable compromise between computation time, GM and WM convergence, resolution effects (due to partial-volume effects), and noise. A further increase in the GM-to-WM contrast ratio would imply an increase in bias in GM and WM, in number of iterations (computation time), and in noise. Results from the inserts phantom experiment indicated that convergence was reached at the same number of iterations (Figs. 1 and 2) as was observed using the Hoffman phantom data (Supplemental Fig. 1). Both ANW-OSEM GM and WM converged to within 1%, compared with 3D-FBP, using 10 iterations. The convergence rate of OP-OSEM was about 1.6 times slower than that of ANW-OSEM, which is slightly better than what has been reported in a previous study using the manufacturer's OP-OSEM (4), in which OP-OSEM was said to converge about 2 times more slowly than ANW-OSEM. Convergence was reached for OP-OSEM using 16 iterations. This convergence is 2 times slower than the version used by the manufacturer, which converges after 3–11 iterations (7), in which 8 iterations were found to be optimal (9) when using the same criteria as used in this study. SP-OSEM also requires 1.6–1.7 times more iterations than does ANW-OSEM, which is slightly faster than the number of iterations reported in previous studies (17). In these 3D studies performed on an ECAT EXACT HR+ scanner (CTI/Siemens), 15 iterations were used for SP-OSEM and 4 for ANW-OSEM. OSWLS converged to an acceptable GM and WM activity concentration after 7 iterations. Although the number of iterations required for sufficient convergence was similar for both the Hoffman and the inserts phantom studies, clinical data were analyzed for various numbers of iterations to further study and demonstrate convergence properties.
Phantom Studies
3D-FBP showed good correspondence to the true activity concentration in short-duration frames of the homogeneous phantom (<2%). Although 3D-FBP showed some bias in cold and hot inserts, observed 3D-FBP biases were less dependent on NEC than biases seen with iterative methods (Supplemental Figs. 1 and 2; Figs. 3 and 4). However, these biases disappeared using the same phantom with contrasts similar to the Hoffman phantom (1:2; data not shown). Moreover, 3D-FBP provided a GM-to-WM contrast independent of NEC (Fig. 4C; Supplemental Fig. 2) in the Hoffman phantom studies, which resemble clinically relevant activity concentration distributions. Deviations in the GM-to-WM contrast were not statistically significant (P > 0.5). 3D-FBP was, therefore, chosen as a reference reconstruction method for further evaluations of Hoffman phantom and clinical studies.
OP-OSEM showed the lowest positive bias (<8%), but COV (<5.1·102%) was twice as high as that for OSWLS (<2.2·102%). In addition, OSWLS showed almost linearly increasing COV at low-frame durations, whereas this variation was larger for all other methods. However, OSWLS showed a higher positive bias (<15%) than did OP-OSEM. The performance of SP-OSEM was similar to that of OP-OSEM, as can be seen from Figure 3. This result is consistent with data from Ahn and Fessler (18), in which SP-OSEM only slightly improved bias over OP-OSEM in 2D simulations. However, as also observed previously (19,32) for simulated 2D transmission and emission scans, SP-OSEM, compared with OP-OSEM, reduced SD up to 11%.
All methods showed similar performance for the Hoffman phantom, with various frame durations, although both OP-OSEM and SP-OSEM showed a lower bias (<75%, P < 0.001) in GM-to-WM contrast ratio between short- and long-duration frames. For the Hoffman phantom decay study, ANW-OSEM performed poorly, with a change in the GM-to-WM contrast ratio of 20%. In a previous study (9), we reported a high-contrast change in the GM-to-WM contrast ratio (54%) using the manufacturer's implementation of OP-OSEM. Using the in-house–implemented OP-OSEM with the same convergence criteria, the same ROI definitions, and the same scan of the Hoffman phantom, we obtained a good (and stable) GM-to-WM contrast ratio (10%), as we did with most other reconstruction methods (between 8% and 10%). SP-OSEM, OP-OSEM, and especially OSWLS showed good agreement with 3D-FBP GM-to-WM contrast ratios (<7% difference).
Human Brain Study
ANW-OSEM showed considerable bias (<109% in WM) for short-duration frames (15–60 s) or low NEC. Other iterative reconstruction techniques reduced bias (<15%), which is consistent with the phantom studies (Figs. 1–4⇑⇑⇑; Supplemental Fig. 1).
Parametric images, reconstructed with 3D-FBP, were noisy, consistent with the phantom data in which a high COV (<1.5·103%) was observed in the short-duration frames of the homogeneous phantom. Therefore, 3D-FBP is not recommended routinely for quantitative brain studies and should be used only to validate iterative reconstruction methods.
Parametric data derived from ANW-OSEM showed that bias had a large effect on parametric results, especially for reference-tissue models in which large underestimations were observed. This is primarily due to bias in the pons time–activity curve (Supplemental Fig. 3C). Consequently, reducing bias, currently observed in iterative reconstruction techniques at low frame durations, is essential for quantitative brain studies.
Visually, OSWLS showed the fewest artifacts in the parametric images. In general, OSWLS showed better correspondence to parametric results obtained with 3D-FBP, especially for reference-tissue models (Table 2; slope with intercept fixed at origin, 1.02; r = 0.99). This result is also consistent with phantom data and the data of Boellaard et al. (11). On the basis of correspondence between GM-to-WM contrast ratios (within 4% when compared with 3D-FBP) over different NECs, low bias in GM regions (<11%, P < 0.001), linearly increasing COV, and good correspondence with the 3D-FBP parametric data (slope with intercept fixed at origin, 1.02 [reference tissue] and 0.93 [plasma input]; r = 0.97–0.99), OSWLS is recommended for 3D HRRT brain scans.
Additional Remarks
11C-flumazenil has the advantage of high extraction and therefore good scan statistics. Use of other tracers with lower extraction, for example, 11C-PK11195, most likely will result in higher bias due to poorer scan statistics. Some bias is still observed for iterative reconstruction methods in short-duration frames that could influence parametric data analysis and could be worse for tracers with low extraction, especially for reference-tissue models in which reference tissue has a low uptake (no specific binding). Also, bias related to contrast, as is still observed for all iterative reconstruction methods, could cause problems with image-derived input functions (33). Therefore, future research should be directed at removing systematic bias, for example, by using iterative reconstructions that allow negative image values, such as negative maximum likelihood (34).
The resolution of clinical scanners will be improved over the next few years. These scanners will therefore likely contain large and sparse sinograms as a result of using smaller crystals and, consequently, may suffer from bias when using iterative reconstructions with nonnegativity constraints. This work may, therefore, be important for future high-resolution PET scanners as well.
CONCLUSION
ANW-OSEM showed high bias in reconstructed activity concentration and parametric images, especially in the case of reference-tissue models. OP-OSEM, SP-OSEM, and OSWLS showed good performance for phantom studies. In addition, OSWLS showed better results for clinical parametric data and is therefore recommended for HRRT brain studies. Future improvements are expected by allowing negative image values in iterative reconstructions.
Acknowledgments
We thank Dr. Christian Michel and Jurgen E.M. Mourik for useful discussions, Prof. Dr. Michel Defrise for the Colsher filter, and Nelleke Tolboom and Saskia P.A. Wolfensberger for handling the patient data. Financial support was provided by the Netherlands Organisation for Scientific Research (NWO), grant 016.066.309.
Footnotes
-
COPYRIGHT © 2009 by the Society of Nuclear Medicine, Inc.
References
- Received for publication March 28, 2008.
- Accepted for publication September 22, 2008.