Research ArticleSpecial Contribution
Open Access

Computational Nuclear Oncology Toward Precision Radiopharmaceutical Therapies: Current Tools, Techniques, and Uncharted Territories

Tahir Yusufaly, Emilie Roncali, Julia Brosch-Lenz, Carlos Uribe, Abhinav K. Jha, Geoffrey Currie, Joyita Dutta, Georges El-Fakhri, Helena McMeekin, Neeta Pandit-Taskar, Jazmin Schwartz, Kuangyu Shi, Lidia Strigari, Habib Zaidi, Babak Saboury and Arman Rahmim
Journal of Nuclear Medicine April 2025, 66 (4) 509-515; DOI: https://doi.org/10.2967/jnumed.124.267927

Abstract

Radiopharmaceutical therapy (RPT), with its targeted delivery of cytotoxic ionizing radiation, demonstrates significant potential for treating a wide spectrum of malignancies, with particularly unique benefits for metastatic disease. There is an opportunity to optimize RPTs and enhance the precision of theranostics by moving beyond a one-size-fits-all approach and using patient-specific image-based dosimetry for personalized treatment planning. Such an approach, however, requires accurate methods and tools for the mathematic modeling and prediction of dose and clinical outcome. To this end, the SNMMI AI-Dosimetry Working Group is promoting the paradigm of computational nuclear oncology: mathematic models and computational tools describing the hierarchy of etiologic mechanisms involved in RPT dose response. This includes radiopharmacokinetics for image-based internal dosimetry and radiobiology for the mapping of dose response to clinical endpoints. The former area originates in pharmacotherapy, whereas the latter originates in radiotherapy. Accordingly, models and methods developed in these predecessor disciplines serve as a foundation on which to develop a repurposed set of tools more appropriate to RPT. Over the long term, this computational nuclear oncology framework also promises to facilitate widespread cross-fertilization of ideas between nuclear medicine and the greater mathematic and computational oncology communities.

Nuclear medicine is in a renaissance through radiopharmaceutical therapies (RPTs) that have demonstrated efficacy, particularly in treatment of advanced metastatic cancers (1–3). Radiopharmaceuticals are administered systemically and deliver radiation locally as molecules preferentially bind to cancer-specific targets.

Current labels of federally approved RPTs, however, follow a one-size-fits-all approach with fixed activities, numbers of cycles, and intercycle time intervals (4,5). This practice neglects patient-specific characteristics that modulate therapeutic response, including biokinetics, risk factors, functional organ reserves, and tumor heterogeneity (6–9). Consequently, the delivered doses to organs or tumor, and resulting outcomes, can vary significantly (10,11), sometimes by orders of magnitude (12,13).

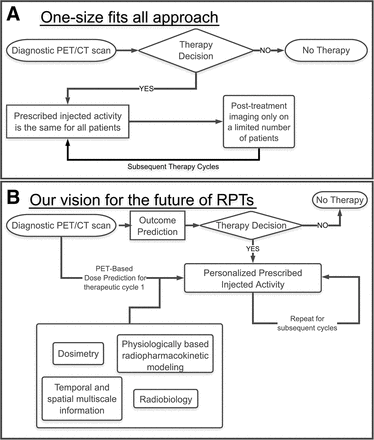
Accordingly, there has been interest in personalizing RPT. Recently, road maps toward this goal have been proposed (7,14), with an emphasis on theranostic digital twins: virtual, patient-specific avatars parameterized with pretreatment diagnostic imaging and clinical input, simulated to prospectively predict dosimetry and outcomes and optimized to design individualized activity prescriptions and treatment plans, including iterative feedback and treatment adaptation between cycles, as shown in Figure 1. The development and implementation of theranostic digital twins require research advancements on many fronts, highlighted by a recent review (7). Examples (15,16) of problems that must be resolved include population-level initialization and patient-specific fine-tuning of model parameters; standardization and harmonization of heterogeneously collected data; and verification, validation, and uncertainty quantification.

FIGURE 1.
FIGURE 1.

Diagram comparing present one-size-fits-all RPT approach (A) with vision of precision RPTs (B). Central to such a future is development of robust models that translate therapeutic inputs to clinical outputs, from which one can prescribe optimal protocols in cycle 1 and refine the process in later cycles to adaptively optimize treatment.

Central to all of these is the identification and selection of robust mathematic models mapping input treatment protocols to predicted clinical outcomes. Therapeutic response to RPT is driven by a combination of 2 ingredients: pharmacokinetics (17,18), which determines the agent biodistribution and resulting physical dose to tumors and organs, and radiation biology (19–21), which translates this spatiotemporal dose distribution to biologic effects, including efficacy and toxicity. These ingredients are relics of RPT’s historic relationship to 2 therapeutic paradigms: pharmacotherapy (for pharmacokinetics) and radiation therapy (for radiobiology). Both of these communities have independently developed mathematic formalisms and computational techniques tailored to their purposes. Thus, integration of methods from these 2 specialties is a promising place to start in identifying an appropriate set of tools for RPT.

However, it is important to realize that this hybridization also endows RPT with unique features that differentiate it from its predecessors. For example, whereas concepts from traditional pharmacokinetics carry over, in RPT we now have the additional feature that the site of action of the therapeutic agent (radiation) is not commensurate with the physiologic biodistribution of the pharmaceutical but also depends on physical characteristics of the emitted radiation tracks in relation to organ anatomy. In addition, the emission of radiation endows us with the unique opportunity to image delivery in real time. Likewise, even though biologic effects are driven by radiation, the radiobiology of external-beam radiation therapy (EBRT) is not directly transferable to RPT, because of differences in spatial and temporal heterogeneity between the 2 modalities. These originate, again, in physiology-mediated biokinetics, which needs to be estimated with nuclear medicine imaging in order to calibrate radiobiologic calculations.

If RPT can be considered related to the predecessor therapies of pharmacotherapy and radiation therapy, then we define computational nuclear oncology (CNO) as the combination of methods from these 2 respective communities, but again with distinct properties originating from nuclear medicine, as illustrated in Figure 2. With this in mind, the goal of the current paper is to review techniques available for mathematic and computational modeling in the predecessor disciplines, with an eye toward how various toolkits must to be adapted and integrated to deal with peculiarities of RPT.

FIGURE 2.
FIGURE 2.

RPT is hybridization of 2 therapeutic paradigms, pharmacotherapy and radiation therapy, but with additional element of physiologically mediated delivery that can be imaged through nuclear medicine. Accordingly, CNO may be considered analogous hybrid of pharmacokinetic modeling and radiobiology-calibrated dosimetry, linked via intermediary of image-based internal dosimetry. PD = pharmacodynamics.

REPURPOSING PHYSIOLOGICALLY BASED PHARMACOKINETICS (PBPK) INTO PHYSIOLOGICALLY BASED RADIOPHARMACOKINETICS (PBRPK) FOR PERSONALIZED RPT DOSIMETRY

Reliable modeling and prediction of pharmacokinetics is the first step toward clinical RPT dosimetry (22–25). The mathematic methods appropriate to this task are rooted in research originating from the drug discovery and development communities (26–28). Particularly relevant to RPT is PBPK modeling. PBPK models represent organs as individual compartments connected via the circulatory system, which facilitates tracer accumulation, transfer, and exchange through mechanisms such as perfusion or permeability constraints. Each organ is further broken down into subcompartments (e.g., interstitial, vascular, and cellular) linked by physical and biochemical pathways. The choice of compartments and level of detail included are specific to each drug or radiopharmaceutical, its biodistribution, and the targeted pathologic process. Reference tissue models, which obviate individual blood concentration calibrations, are also a viable approach.

PBPK models have a rich tradition in pharmacology and are now a routine tool for in silico drug discovery and development (26). The diffusion of PBPK into the RPT community is a more recent phenomenon (23,25) that has opened a wide array of exciting opportunities. It has also, however, introduced new challenges arising from the idiosyncrasies of radiopharmaceuticals.

Most notably, RPT delivers therapy nonlocally via the emission of radiation tracks, which propagate to distal targets throughout the body. Thus, PBPK models of the radioactive emitter must also be paired with internal dosimetry (29,30), which translates the biodistribution in different source organs to the resulting absorbed dose (AD) to biologic targets. Such calculations are intricate, necessitating the consideration of multiple factors (31), including the isotope’s decay scheme, including energy, emitted particle, and decay branching ratios; particle range and half-life; the material, typically biologic tissue, where decay occurs and energy is deposited; and the total number of disintegrations in the tissue. Approaches to internal dosimetry in RPT range from organ-level S values (32–34) to detailed 3-dimensional approaches, such as voxel S values (35–37) and Monte Carlo simulations (38–40). The inclusion of dosimetry distinguishes pharmacokinetic modeling in RPT from more conventional pharmaceuticals. Furthermore, in RPT, hot and cold pharmaceuticals interact though decay as well as through competition in binding to receptors (25,41), which distinguishes such modeling sufficiently to justify its own name: PBRPK.

In addition, radiopharmaceuticals also differ from more traditional agents by being traceable after administration via molecular imaging (42,43), which quantifies accumulation and clearance of the radiopharmaceutical in different tissues over time. Thus, RPT offers possibilities for real-time imaging and assessment of the therapeutic biodistribution via simultaneous emission of photons. Common techniques for this include conjugate-view γ-camera imaging, SPECT, and hybrid SPECT/planar imaging (44), with SPECT demonstrating superior accuracy (45,46). Furthermore, RPT also allows for prospective dose prediction in addition to retrospective dose assessment (47–49). By exploiting newly introduced high-sensitivity long-axial-field-of-view and total-body PET scanners (50–52), multiple-time-point and delayed pretherapy scans can be used to infer individual-patient time–activity curves for theranostic pairs (53). Notably, these recent innovations allow us, for the first time, to observe pharmacokinetic dynamics spanning multiple timescales simultaneously, including both conventional drug biodistribution and clearance operating over the course of several hours or days, along with more rapid uptake and washout processes that take place over shorter timespans of 1–2 h.

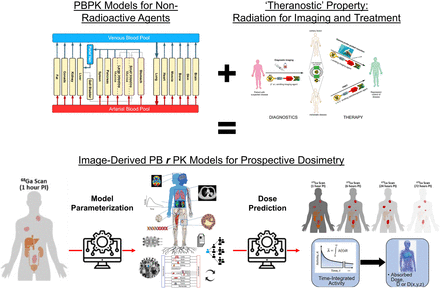
Collectively, these efforts will lead to a future CNO pipeline, illustrated in Figure 3, where pretherapy image-derived time–activity curves from the diagnostic can be used to extrapolate and parametrize a PBRPK model for the therapeutic. The resulting model can be used to prospectively predict, for a given choice of therapeutic protocol actions, the AD to tumors and normal organs. Paired with appropriate models for translating AD to clinical endpoints (to be discussed in the next section), clinicians can tweak protocol actions to optimize therapeutic efficacy.

FIGURE 3.
FIGURE 3.

PBPK modeling and simulation from drug discovery and development communities can be applied to enable RPT dosimetry via theranostic principle, which enables estimation of patient-specific pharmacokinetics with pretherapy PET imaging, and use these models to help prospectively predict patient-specific therapeutic doses that can be verified with real-time SPECT imaging. PI = after injection. (PBPK figure adapted from (118), theranostics schematic adapted from (119), diagnostic PET and therapeutic SPECT cartoons adapted from (120), model-parameterized PBRPK network adapted from (8), and time-integrated activity–to–AD diagram adapted from (121).)

Image-based PBRPK modeling and dosimetry have already been applied to several interesting questions. Examples include studies on the effects of vascular perfusion and receptor density on tumor delivery (54); the effects of ligand amount, affinity, and internalization on AD (55,56); the effects of time-point image sampling on quantitative measures (57); the effect of tumor volume on AD in kidneys and tumors (58); the prediction of therapeutic biodistribution from biokinetics, tumor volume, and glomerular filtration rate (59); and the impact of administration scheduling, including single versus multiple-bolus injections, on AD (25).

RECALIBRATING EBRT RADIOBIOLOGY FOR MULTISCALE RPT DOSIMETRY

After image-based pharmacokinetic estimation of AD, the remaining step in the CNO pipeline is to translate this AD to clinical outcomes. In EBRT, this goal is achieved using the methods of radiobiology (60,61). Radiation kills cells by causing DNA damage through mechanisms that include direct ionization, free radical generation, and activation of secondary processes. Double-strand breaks are particularly harmful, leading to genetic information loss and incorrect rejoining, which are often lethal. Factors such as cell proliferation, differentiation, and DNA repair capabilities determine the radiosensitivity of a cell, which is also modified by dose rate, oxygenation, and linear energy transfer.

The most commonly used clinical model in EBRT for these effects is the linear-quadratic model (62), sometimes modified to incorporate factors such as incomplete repair of sublethal damage. This model serves as a springboard for deriving (63) the biologic effective dose, which may be thought of as a local calibration of the spatiotemporal dose distribution to the cells in a microscopic subvolume of the organ or tumor. The remaining step is to translate the overall distribution of the biologic effective dose across the structure into an overall tumor control probability or normal-tissue complication probability. Essential in this is consideration of the specific clinical endpoint and the extent to which the organ behaves serially (strong codependence of the functional subunits) versus parallelly (the functional subunits behaving mostly autonomously). The tumor control probability and normal-tissue complication probability serve as conceptual underpinnings (64,65) of the physical and dosimetric constraints built into modern EBRT treatment planning software, such as Varian RapidPlan (66) or Accuray RayStation (67).

A pressing challenge for RPT, however, is that the radiobiologic knowledge and assumptions built into EBRT treatment planning are specifically configured for that modality. Currently, with limited data, RPT often assumes EBRT-derived dose limits. Although in some cases (e.g., long-ranged β-emitting RPT with dose-rate biologic effective dose corrections) such approaches might be reasonable, it is generally agreed that the black-box application of EBRT paradigms hinders the long-term development of RPT and leads to suboptimal outcomes (68). Radiobiologic effects in RPT (20,21) arise from distinct patterns of particle type, energy, transport, range, and dose rate originating in pharmacokinetics, which shapes dose in a way that is fundamentally different from EBRT (69,70). As a result, the extent to which models and assumptions used in EBRT can be extrapolated remain unclear.

This is especially important for α-emitters because of the prevalence of microdosimetric fluctuations at the cellular and subcellular levels, phenomena that have no analog in photon EBRT. Relatedly, understanding differences in DNA repair, cell death, and cell cycle effects between the 2 modalities is essential. It is known that these processes are sensitive to microenvironmental variations, such as tumor hypoxia and vasculature or infiltration of immune cells and products. Given the differences in radiation delivery between RPT and EBRT, it is reasonable to assume that any radiation-induced alterations to this microenvironment would also differ. Nuclear medicine, incidentally, is well suited to imaging such changes in order to quantify biologic effectiveness.

Accordingly, developing robust methodologies to adapt EBRT-based radiobiology to RPT, or create new RPT-specific models de novo, is imperative. A good starting point to this end, illustrated in Figure 4, is to interface quantitative radiobiology with PBRPK-derived inferences of the microscale dose distributions, with all biologic effective dose, tumor control probability, and normal-tissue complication probability models adjusted (71–73) to correct for the differences in RPT and EBRT. This interfacing, however, is made challenging by the need to model and the coupling of dosimetric processes across multiple scales (74–76). Current image-derived PBRPK dosimetry yields information on mean organ or tumor ADs or on ADs per voxel of several-millimeter size. On the other hand, radiobiologic modeling starts with DNA damage and cell death in tissues, processes that occur at the microscale and nanoscale.

FIGURE 4.
FIGURE 4.

Concepts, tools, and models of external-beam radiobiology, from which much of modern EBRT treatment planning is based, must be modified for RPT because of physiologically mediated small-scale biodistribution and dosimetry, which modify radiation response via series of complex and incompletely understood mechanisms. RPT-adapted radiobiologic modeling must ultimately be paired with suitably estimated multiscale extrapolation to enable robust end-to-end prediction of clinical outcome, illustrated here for the example of acute kidney injury. AKD = acute kidney disease; AKI = acute kidney injury; CKD = chronic kidney disease; CVD = cardiovascular disease; IM = inner medulla; ISOM = inner strip of outer medulla; OSOM = outer strip of outer medulla. (Multiscale anatomy diagrams adapted from (122), acute injury dynamic function schematic adapted from (123), PET/CT adapted from (124), and multiscale dosimetry figure adapted from (125).)

Various approaches exist for extrapolating observable organ-level energies to doses at the suborgan (77,78), voxel (79), cellular (73), and molecular (80,81) levels. Incorporating these subresolution nonuniformities into the radiobiologic simulations will be important for reliable outcome prediction. These subgrid extrapolation schemes are typically measured in vitro using preclinical animal models (82). Examples of common software packages used in performing such tasks include GEANT4 (83) and its extensions (81,84), MCNP (85,86), FLUKA (87), PENELOPE (88,89), and various components in the MIRDsoft platform (90).

However, in their present form, these tools are mostly of academic interest, and additional work is critically needed to bridge them with clinical tools (44), examples including Rapid (91) or Voximetry (92). It is encouraging that this area has recently seen an increase in activity, particularly in Europe (21,93–95). Building on this momentum, future work should prioritize preclinical investigations of small-scale radiopharmaceutical distribution, radiation-induced DNA damage and repair, and the coupling of macroscopic imaging with these microscopic data. A noteworthy example to this end built a cellular-level dosimetry model for targeted α-therapy with Monte Carlo simulations, which was experimentally validated in vitro for 212Pb (96).

FORWARD-LOOKING VISION: CNO AS A BASIS FOR CROSS-SPECIALTY DIGITAL TWINS

The previous sections have reviewed computational predecessors of CNO, describing how they must be adapted for RPT. In so doing, we have highlighted how prospective image-based PBRPK dosimetry can calculate tumor and organ AD and how radiobiologic calculations supplemented by small-scale subgrid dosimetry models can translate AD into observed clinical effects for treatment optimization. It is encouraging to see the progress that has already been made in each of these pieces. The natural next step is to sync the pieces together and interface the models with real-world clinical data, including validation, verification, and uncertainty quantification (97,98). The timing for these efforts is ripe, given the recent calls in the RPT community (68,99) for more robust data collection and standardized reporting of imaging, dosimetry, and outcomes. The myriad technical and logistic challenges that must be addressed to this end have been reviewed elsewhere (3,100).

We would like to draw attention to an intriguing, but often neglected, ancillary benefit of theranostic digital twins and the underlying CNO framework discussed herein. In this review, we have emphasized links between modeling paradigms from the communities of pharmacotherapy and radiation therapy to RPT. The resulting tools can serve as a powerful unifying framework for cross-institutional data sharing and model building across nuclear medicine clinics. However, in addition to facilitating intramodality sharing within the RPT community, CNO is also a natural language for facilitating intermodality sharing and cross-disciplinary fertilization with other medical specialties. The desire and push for data-driven modeling and digital twin personalization is not unique to nuclear medicine (101–103), and the medical subspecialities associated with the predecessor disciplines of CNO—medical oncology for pharmacotherapy (104,105) and radiation oncology for radiation therapy (106,107)—have also seen recent enthusiasm for digital twins. By emphasizing the relationship of RPT to these specialties, CNO will allow the nuclear medicine community to pursue appropriate stewardship of RPTs while also being able to synergistically interact with medical “relatives.”

This will also serve as a gateway for more regular cross-fertilization across the greater computational and mathematic oncology community. The application of mathematics to cancer biology and treatment response has a rich history, and recent years have seen an explosive number of breakthroughs in the field. Examples of such progress include ordinary differential equation models of tumor growth and response (108), partial differential equation models of tissue reorganization and metastasis (109), agent-based models of intercellular interactions and behavior (110), stochastic models of tumor ecoevolutionary extinction (111), and game-theoretic optimization of combination and adaptive therapies (112). Clearly, nuclear medicine and the RPT community have much to gain by synergizing with the state-of-the-art mathematic and computational modeling tools. CNO, as such, will facilitate the interdisciplinary communications necessary to realizing these gains.

CONCLUDING THOUGHTS

In this article, we have introduced CNO as a computational modeling approach that will ultimately enable personalization of RPTs via theranostic digital twins. Our exposition highlighted how RPT includes elements of both pharmacotherapy and radiation therapy but maintains its unique identity. These interdisciplinary origins, moreover, will help guide the nuclear medicine community in further adapting and integrating computational tools from other communities into the CNO toolkit.

As a final comment, it is irresistible to point out analogies and similarities between this discussion and the machine learning areas of large language models, foundation models, and artificial general intelligence (113,114). Interest in these fields is predicated on the idea that models trained on specific data modalities for particular tasks can be repurposed, via transfer learning and other methods (115), for application to new data modalities and tasks. Identifying which features are task- and modality-specific, and determining what can and cannot be transferred, is very much akin to the way CNO keeps certain elements from its predecessors while discarding others. One of the important lessons learned throughout the larger oncology community is that there is no magic bullet for cancer (116,117). A truly long-term approach to treatment will require a multipronged strategy as flexible and adaptive as the tumor being treated (112). Such visions are exciting to dream about but challenging to operationalize. We believe that CNO, and how it connects RPT to pharmacotherapy and radiation therapy while emphasizing its distinctiveness, will serve as an example to the medical community on how to practically realize these goals.

DISCLOSURE

Arman Rahmim and Carlos Uribe are cofounders of Ascinta Technologies Inc. No other potential conflict of interest relevant to this article was reported.

ACKNOWLEDGMENTS

We thank Bonnie Clarke and Lance Burrell for their continuous support.

Footnotes

  • Published online Feb. 13, 2025.

Immediate Open Access: Creative Commons Attribution 4.0 International License (CC BY) allows users to share and adapt with attribution, excluding materials credited to previous publications. License: https://creativecommons.org/licenses/by/4.0/. Details: https://jnm.snmjournals.org/page/permissions.

REFERENCES

  1. 1.↵
    1. Sgouros G,
    2. Bodei L,
    3. McDevitt MR,
    4. Nedrow JR
    . Radiopharmaceutical therapy in cancer: clinical advances and challenges. Nat Rev Drug Discov. 2020;19:589–608.
    OpenUrlCrossRefPubMed
  2. 2.
    1. St James S,
    2. Bednarz B,
    3. Benedict S,
    4. et al
    . Current status of radiopharmaceutical therapy. Int J Radiat Oncol Biol Phys. 2021;109:891–901.
    OpenUrlPubMed
  3. 3.↵
    1. Divgi C,
    2. Carrasquillo JA,
    3. Meredith R,
    4. et al
    . Overcoming barriers to radiopharmaceutical therapy (RPT): an overview from the NRG-NCI working group on dosimetry of radiopharmaceutical therapy. Int J Radiat Oncol Biol Phys. 2021;109:905–912.
    OpenUrlPubMed
  4. 4.↵
    1. Garin E,
    2. Tselikas L,
    3. Guiu B,
    4. et al
    .; DOSISPHERE-01 study group. Personalised versus standard dosimetry approach of selective internal radiation therapy in patients with locally advanced hepatocellular carcinoma (DOSISPHERE-01): a randomised, multicentre, open-label phase 2 trial. Lancet Gastroenterol Hepatol. 2021;6:17–29.
    OpenUrlCrossRefPubMed
  5. 5.↵
    1. Graves SA,
    2. Hobbs RF
    . Dosimetry for optimized, personalized radiopharmaceutical therapy. Semin Radiat Oncol. 2021;31:37–44.
    OpenUrlPubMed
  6. 6.↵
    1. Brosch-Lenz J,
    2. Yousefirizi F,
    3. Zukotynski K,
    4. et al
    . Role of artificial intelligence in theranostics:: toward routine personalized radiopharmaceutical therapies. PET Clin. 2021;16:627–641.
    OpenUrlPubMed
  7. 7.↵
    1. Abdollahi H,
    2. Yousefirizi F,
    3. Shiri I,
    4. et al
    . Theranostic digital twins: concept, framework and roadmap towards personalized radiopharmaceutical therapies. Theranostics. 2024;14:3404–3422.
    OpenUrlPubMed
  8. 8.↵
    1. Rahmim A,
    2. Brosch-Lenz J,
    3. Fele-Paranj A,
    4. et al
    . Theranostic digital twins for personalized radiopharmaceutical therapies: reimagining theranostics via computational nuclear oncology. Front Oncol. 2022;12:1062592.
    OpenUrlPubMed
  9. 9.↵
    1. Brosch-Lenz J,
    2. Uribe C,
    3. Rahmim A,
    4. Saboury B
    . Theranostic digital twins: an indispensable prerequisite for personalized cancer care [letter]. J Nucl Med. 2023;64:501.
    OpenUrlFREE Full Text
  10. 10.↵
    1. Uribe C,
    2. Peterson A,
    3. Van B,
    4. et al
    . An international study of factors affecting variability of dosimetry calculations, part 1: design and early results of the SNMMI dosimetry challenge. J Nucl Med. 2021;62(suppl 3):36S–47S.
    OpenUrl
  11. 11.↵
    1. Brosch-Lenz J,
    2. Ke S,
    3. Wang H,
    4. et al
    . An international study of factors affecting variability of dosimetry calculations, part 2: overall variabilities in absorbed dose. J Nucl Med. 2023;64:1109–1116.
    OpenUrlAbstract/FREE Full Text
  12. 12.↵
    1. Violet J,
    2. Jackson P,
    3. Ferdinandus J,
    4. et al
    . Dosimetry of 177Lu-PSMA-617 in metastatic castration-resistant prostate cancer: correlations between pretherapeutic imaging and whole-body tumor dosimetry with treatment outcomes. J Nucl Med. 2019;60:517–523.
    OpenUrlAbstract/FREE Full Text
  13. 13.↵
    1. Del Prete M,
    2. Buteau F-A,
    3. Arsenault F,
    4. et al
    . Personalized 177Lu-octreotate peptide receptor radionuclide therapy of neuroendocrine tumours: initial results from the P-PRRT trial. Eur J Nucl Med Mol Imaging. 2019;46:728–742.
    OpenUrlPubMed
  14. 14.↵
    1. Abdollahi H,
    2. Rahmim A
    . Digital twins for personalized healthcare: application to radiopharmaceutical therapies. Front Biomed Technol. 2023;10:1–5.
  15. 15.↵
    1. Alber M,
    2. Buganza Tepole A,
    3. Cannon WR,
    4. et al
    . Integrating machine learning and multiscale modeling: perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. NPJ Digit Med. 2019;2:115.
    OpenUrlPubMed
  16. 16.↵
    Committee on Foundational Research Gaps and Future Directions for Digital Twins, Board on Mathematical Sciences and Analytics, Committee on Applied and Theoretical Statistics, et al. Foundational Research Gaps and Future Directions for Digital Twins. National Academies Press; 2023:26894.
  17. 17.↵
    1. Currie GM
    . Pharmacology, part 2: introduction to pharmacokinetics. J Nucl Med Technol. 2018;46:221–230.
    OpenUrlAbstract/FREE Full Text
  18. 18.↵
    1. Sunderland JJ,
    2. Ponto LB,
    3. Capala J
    . Radiopharmaceutical delivery for theranostics: pharmacokinetics and pharmacodynamics. Semin Radiat Oncol. 2021;31:12–19.
    OpenUrlPubMed
  19. 19.↵
    1. Pouget J-P,
    2. Lozza C,
    3. Deshayes E,
    4. Boudousq V,
    5. Navarro-Teulon I
    . Introduction to radiobiology of targeted radionuclide therapy. Front Med. 2015;2:12.
  20. 20.↵
    1. Morris ZS,
    2. Wang AZ,
    3. Knox SJ
    . The radiobiology of radiopharmaceuticals. Semin Radiat Oncol. 2021;31:20–27.
    OpenUrlCrossRefPubMed
  21. 21.↵
    1. Aerts A,
    2. Eberlein U,
    3. Holm S,
    4. et al
    . EANM position paper on the role of radiobiology in nuclear medicine. Eur J Nucl Med Mol Imaging. 2021;48:3365–3377.
    OpenUrlPubMed
  22. 22.↵
    1. Kotasidis FA,
    2. Tsoumpas C,
    3. Rahmim A
    . Advanced kinetic modelling strategies: towards adoption in clinical PET imaging. Clin Transl Imaging. 2014;2:219–237.
    OpenUrlPubMed
  23. 23.↵
    1. Paranj AF,
    2. Brosch-Lenz J,
    3. Uribe C,
    4. Rahmim A,
    5. Saboury B
    . Modular model architecture for radiopharmaceutical therapy planning: physiologically-based radiopharmacokinetics (PBRPK) implementation. J Nucl Med. 2022;63:3197–3197.
    OpenUrl
  24. 24.
    1. Siebinga H,
    2. de Wit-van der Veen BJ,
    3. Stokkel MDM,
    4. Huitema ADR,
    5. Hendrikx JJMA
    . Current use and future potential of (physiologically based) pharmacokinetic modelling of radiopharmaceuticals: a review. Theranostics. 2022;12:7804–7820.
    OpenUrlPubMed
  25. 25.↵
    1. Fele-Paranj A,
    2. Saboury B,
    3. Uribe C,
    4. Rahmim A
    . Physiologically based radiopharmacokinetic (PBRPK) modeling to simulate and analyze radiopharmaceutical therapies: studies of non-linearities, multi-bolus injections, and albumin binding. EJNMMI Radiopharm Chem. 2024;9:6.
    OpenUrlPubMed
  26. 26.↵
    1. Jones HM,
    2. Gardner IB,
    3. Watson KJ
    . Modelling and PBPK simulation in drug discovery. Aaps J. 2009;11:155–166.
    OpenUrlCrossRefPubMed
  27. 27.
    1. Sager JE,
    2. Yu J,
    3. Ragueneau-Majlessi I,
    4. Isoherranen N
    . Physiologically based pharmacokinetic (PBPK) modeling and simulation approaches: a systematic review of published models, applications, and model verification. Drug Metab Dispos. 2015;43:1823–1837.
    OpenUrlAbstract/FREE Full Text
  28. 28.↵
    1. Elmokadem A,
    2. Zhang Y,
    3. Knab T,
    4. Jordie E,
    5. Gillespie WR
    . Bayesian PBPK modeling using R/Stan/Torsten and Julia/SciML/Turing.Jl. CPT Pharmacometrics Syst Pharmacol. 2023;12:300–310.
    OpenUrlPubMed
  29. 29.↵
    1. Strigari L,
    2. Konijnenberg M,
    3. Chiesa C,
    4. et al
    . The evidence base for the use of internal dosimetry in the clinical practice of molecular radiotherapy. Eur J Nucl Med Mol Imaging. 2014;41:1976–1988.
    OpenUrlCrossRefPubMed
  30. 30.↵
    1. Hofmann W,
    2. Li WB,
    3. Friedland W,
    4. et al
    . Internal microdosimetry of alpha-emitting radionuclides. Radiat Environ Biophys. 2020;59:29–62.
    OpenUrlPubMed
  31. 31.↵
    1. Rossi HH,
    2. Zaider M
    . Microdosimetry and Its Applications. Springer; 1996.
  32. 32.↵
    1. Goddu SM,
    2. Howell RW,
    3. Rao DV
    . Cellular dosimetry: absorbed fractions for monoenergetic electron and alpha particle sources and S-values for radionuclides uniformly distributed in different cell compartments. J Nucl Med. 1994;35:303–316.
    OpenUrlAbstract/FREE Full Text
  33. 33.
    1. Bolch WE,
    2. Eckerman KF,
    3. Sgouros G,
    4. Thomas SR
    . MIRD pamphlet no. 21: a generalized schema for radiopharmaceutical dosimetry—standardization of nomenclature. J Nucl Med. 2009;50:477–484.
    OpenUrlAbstract/FREE Full Text
  34. 34.↵
    1. Olguin E,
    2. President B,
    3. Ghaly M,
    4. Frey E,
    5. Sgouros G,
    6. Bolch WE
    . Specific absorbed fractions and radionuclide S-values for tumors of varying size and composition. Phys Med Biol. 2020;65:235015.
    OpenUrlPubMed
  35. 35.↵
    1. Malaroda A,
    2. Flux GD,
    3. Buffa FM,
    4. Ott RJ
    . Multicellular dosimetry in voxel geometry for targeted radionuclide therapy. Cancer Biother Radiopharm. 2003;18:451–461.
    OpenUrlCrossRefPubMed
  36. 36.
    1. Lee MS,
    2. Kim JH,
    3. Paeng JC,
    4. et al
    . Whole-body voxel-based personalized dosimetry: the multiple voxel S-value approach for heterogeneous media with nonuniform activity distributions. J Nucl Med. 2018;59:1133–1139.
    OpenUrlPubMed
  37. 37.↵
    1. Graves SA,
    2. Flynn RT,
    3. Hyer DE
    . Dose point kernels for 2,174 radionuclides. Med Phys. 2019;46:5284–5293.
    OpenUrlPubMed
  38. 38.↵
    1. Hobbs RF,
    2. Baechler S,
    3. Fu D-X,
    4. et al
    . A model of cellular dosimetry for macroscopic tumors in radiopharmaceutical therapy: a cellular tumor Monte Carlo model. Med Phys. 2011;38:2892–2903.
    OpenUrlCrossRefPubMed
  39. 39.
    1. Lim A,
    2. Andriotty M,
    3. Yusufaly T,
    4. Agasthya G,
    5. Lee B,
    6. Wang C
    . A fast Monte Carlo cell-by-cell simulation for radiobiological effects in targeted radionuclide therapy using pre-calculated single-particle track standard DNA damage data. Front Nucl Med. 2023;3:1284558.
    OpenUrlPubMed
  40. 40.↵
    1. Auditore L,
    2. Amato E,
    3. Italiano A,
    4. Arce P,
    5. Campennì A,
    6. Baldari S
    . Internal dosimetry for TARE therapies by means of GAMOS Monte Carlo simulations. Phys Med. 2019;64:245–251.
    OpenUrlPubMed
  41. 41.↵
    1. Rahmim A,
    2. Abdollahi H,
    3. Paranj AF,
    4. Lee K-N,
    5. Saboury B,
    6. Uribe C
    . Towards non-tracer kinetic modeling: our past returning through the future [abstract]. J Nucl Med. 2023;64(suppl 1):P1447.
    OpenUrlPubMed
  42. 42.↵
    1. Dewaraja YK,
    2. Frey EC,
    3. Sgouros G,
    4. et al
    . MIRD pamphlet no. 23: quantitative SPECT for patient-specific 3-dimensional dosimetry in internal radionuclide therapy. J Nucl Med. 2012;53:1310–1325.
    OpenUrlAbstract/FREE Full Text
  43. 43.↵
    1. Dewaraja YK,
    2. Ljungberg M,
    3. Green AJ,
    4. et al
    .; SNMMI MIRD committee. MIRD pamphlet no. 24: guidelines for quantitative 131I SPECT in dosimetry applications. J Nucl Med. 2013;54:2182–2188.
    OpenUrlAbstract/FREE Full Text
  44. 44.↵
    1. Capala J,
    2. Graves SA,
    3. Scott A,
    4. et al
    . Dosimetry for radiopharmaceutical therapy: current practices and commercial resources. J Nucl Med. 2021;62(suppl 3):3S–11S.
    OpenUrlPubMed
  45. 45.↵
    1. He B,
    2. Du Y,
    3. Segars WP,
    4. et al
    . Evaluation of quantitative imaging methods for organ activity and residence time estimation using a population of phantoms having realistic variations in anatomy and uptake. Med Phys. 2009;36:612–619.
    OpenUrlCrossRefPubMed
  46. 46.↵
    1. Beauregard J-M,
    2. Hofman MS,
    3. Pereira JM,
    4. Eu P,
    5. Hicks RJ
    . Quantitative 177Lu SPECT (QSPECT) imaging using a commercially available SPECT/CT system. Cancer Imaging. 2011;11:56–66.
    OpenUrlCrossRefPubMed
  47. 47.↵
    1. Akhavanallaf A,
    2. Peterson AB,
    3. Fitzpatrick K,
    4. et al
    . The predictive value of pretherapy [68Ga]Ga-DOTA-TATE PET and biomarkers in [177Lu]Lu-PRRT tumor dosimetry. Eur J Nucl Med Mol Imaging. 2023;50:2984–2996.
    OpenUrlPubMed
  48. 48.
    1. Kassar M,
    2. Drobnjakovic M,
    3. Birindelli G,
    4. et al
    . PBPK-adapted deep learning for pre-therapy prediction of voxel-wise dosimetry: in-silico proof-of-concept. IEEE Trans Radiat Plasma Med Sci. 2024;8:646–654.
  49. 49.↵
    1. Moreau J,
    2. Wang C,
    3. Wong KK,
    4. Blakkisrud J,
    5. Dewaraja Y
    . Predicting 177Lu-DOTATATE SPECT derived red marrow dosimetry from pretherapy 68Ga-DOTATATE PET and baseline biomarkers [abstract]. J Nucl Med. 2024;65(suppl 2):241724.
    OpenUrl
  50. 50.↵
    1. Cherry SR,
    2. Jones T,
    3. Karp JS,
    4. Qi J,
    5. Moses WW,
    6. Badawi RD
    . Total-body PET: maximizing sensitivity to create new opportunities for clinical research and patient care. J Nucl Med. 2018;59:3–12.
    OpenUrlAbstract/FREE Full Text
  51. 51.
    1. Katal S,
    2. Eibschutz LS,
    3. Saboury B,
    4. Gholamrezanezhad A,
    5. Alavi A
    . Advantages and applications of total-body PET scanning. Diagnostics. 2022;12:426.
    OpenUrlPubMed
  52. 52.↵
    1. Lee K-N,
    2. Rahmim A,
    3. Uribe C
    . Novel method to estimate kinetic microparameters from dynamic whole-body imaging in regular-axial field-of-view PET scanners. arXiv website. https://arxiv.org/abs/2404.10197. Published April 16, 2024. Revised May 13, 2024. Accessed February 3, 2025.
  53. 53.↵
    1. Ivashchenko OV,
    2. O’Doherty J,
    3. Hardiansyah D,
    4. et al
    . Time-Activity data fitting in molecular radiotherapy: methodology and pitfalls. Phys Med. 2024;117:103192.
    OpenUrlPubMed
  54. 54.↵
    1. Jiménez-Franco LD,
    2. Glatting G,
    3. Prasad V,
    4. Weber WA,
    5. Beer AJ,
    6. Kletting P
    . Effect of tumor perfusion and receptor density on tumor control probability in 177Lu-DOTATATE therapy: an in silico analysis for standard and optimized treatment. J Nucl Med. 2021;62:92–98.
    OpenUrlAbstract/FREE Full Text
  55. 55.↵
    1. Kletting P,
    2. Schuchardt C,
    3. Kulkarni HR,
    4. et al
    . Investigating the effect of ligand amount and injected therapeutic activity: a simulation study for 177Lu-labeled PSMA-targeting peptides. Plos One. 2016;11:e0162303.
    OpenUrlPubMed
  56. 56.↵
    1. Begum NJ,
    2. Glatting G,
    3. Wester H-J,
    4. Eiber M,
    5. Beer AJ,
    6. Kletting P
    . The effect of ligand amount, affinity and internalization on PSMA-targeted imaging and therapy: a simulation study using a PBPK model. Sci Rep. 2019;9:20041.
    OpenUrlPubMed
  57. 57.↵
    1. Rinscheid A,
    2. Kletting P,
    3. Eiber M,
    4. Beer AJ,
    5. Glatting G
    . Influence of sampling schedules on [177Lu]Lu-PSMA dosimetry. EJNMMI Phys. 2020;7:41.
    OpenUrlPubMed
  58. 58.↵
    1. Begum NJ,
    2. Thieme A,
    3. Eberhardt N,
    4. et al
    . The effect of total tumor volume on the biologically effective dose to tumor and kidneys for 177 Lu-labeled PSMA peptides. J Nucl Med. 2018;59:929–933.
    OpenUrlAbstract/FREE Full Text
  59. 59.↵
    1. Hardiansyah D,
    2. Maass C,
    3. Attarwala AA,
    4. et al
    . The role of patient-based treatment planning in peptide receptor radionuclide therapy. Eur J Nucl Med Mol Imaging. 2016;43:871–880.
    OpenUrlPubMed
  60. 60.↵
    1. Hall EJ
    . Radiobiology for the Radiologist. 3rd ed. Lippincott; 1988.
  61. 61.↵
    1. Joiner MC,
    2. van der Kogel AJ
    , eds. Basic Clinical Radiobiology. 6th ed. CRC Press; 2025.
  62. 62.↵
    1. McMahon SJ
    . The linear quadratic model: usage, interpretation and challenges. Phys Med Biol. 2018;64:01TR01.
    OpenUrlCrossRefPubMed
  63. 63.↵
    1. Fowler JF
    . The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 1989;62:679–694.
    OpenUrlAbstract/FREE Full Text
  64. 64.↵
    1. Palma G,
    2. Monti S,
    3. Conson M,
    4. Pacelli R,
    5. Cella L
    . Normal tissue complication probability (NTCP) models for modern radiation therapy. Semin Oncol. 2019;46:210–218.
    OpenUrlPubMed
  65. 65.↵
    1. Allen Li X,
    2. Alber M,
    3. Deasy JO,
    4. et al
    . The use and QA of biologically related models for treatment planning: short report of the TG-166 of the therapy physics committee of the AAPM—TG-166 report. Med Phys. 2012;39:1386–1409.
    OpenUrlPubMed
  66. 66.↵
    1. Fogliata A,
    2. Cozzi L,
    3. Reggiori G,
    4. et al
    . RapidPlan knowledge based planning: iterative learning process and model ability to steer planning strategies. Radiat Oncol. 2019;14:187.
    OpenUrlCrossRefPubMed
  67. 67.↵
    1. Bodensteiner D
    . RayStation: external beam treatment planning system. Med Dosim. 2018;43:168–176.
    OpenUrlPubMed
  68. 68.↵
    1. Kiess AP,
    2. O’Donoghue J,
    3. Uribe C,
    4. et al
    .; RPT-TEC group. How can radiopharmaceutical therapies reach their full potential? Improving dose reporting and phase I clinical trial design. J Clin Oncol. March 2024;42:1734–1737.
    OpenUrlPubMed
  69. 69.↵
    1. Strand S,
    2. Zanzonico P,
    3. Johnson TK
    . Pharmacokinetic modeling. Med Phys. 1993;20:515–527.
    OpenUrlCrossRefPubMed
  70. 70.↵
    1. English KK,
    2. Knox S,
    3. Graves SA,
    4. Kiess AP
    . Basics of physics and radiobiology for radiopharmaceutical therapies. Pract Radiat Oncol. 2022;12:289–293.
    OpenUrlPubMed
  71. 71.↵
    1. Hobbs RF,
    2. Wahl RL,
    3. Frey EC,
    4. et al
    . Radiobiologic optimization of combination radiopharmaceutical therapy applied to myeloablative treatment of non-Hodgkin lymphoma. J Nucl Med. 2013;54:1535–1542.
    OpenUrlAbstract/FREE Full Text
  72. 72.
    1. Hobbs RF,
    2. Howell RW,
    3. Song H,
    4. Baechler S,
    5. Sgouros G
    . Redefining relative biological effectiveness in the context of the EQDX formalism: implications for alpha-particle emitter therapy. Radiat Res. 2014;181:90–98.
    OpenUrlPubMed
  73. 73.↵
    1. Katugampola S,
    2. Wang J,
    3. Rosen A,
    4. Howell RW
    ; SNMMI MIRD committee. MIRD pamphlet no. 27: MIRDcell V3, a revised software tool for multicellular dosimetry and bioeffect modeling. J Nucl Med. 2022;63:1441–1449.
    OpenUrlAbstract/FREE Full Text
  74. 74.↵
    1. Roeske JC,
    2. Aydogan B,
    3. Bardies M,
    4. Humm JL
    . Small-scale dosimetry: challenges and future directions. Semin Nucl Med. 2008;38:367–383.
    OpenUrlCrossRefPubMed
  75. 75.
    1. Sgouros G,
    2. Roeske JC,
    3. McDevitt MR,
    4. et al
    .; SNM MIRD committee. MIRD pamphlet no. 22 (abridged): radiobiology and dosimetry of -particle emitters for targeted radionuclide therapy. J Nucl Med. 2010;51:311–328.
    OpenUrlAbstract/FREE Full Text
  76. 76.↵
    1. Sgouros G,
    2. Hobbs RF,
    3. Atkins FB,
    4. Van Nostrand D,
    5. Ladenson PW,
    6. Wahl RL
    . Three-dimensional radiobiological dosimetry (3D-RD) with 124I PET for 131I therapy of thyroid cancer. Eur J Nucl Med Mol Imaging. 2011;38:41–47.
    OpenUrl
  77. 77.↵
    1. Snyder WS,
    2. Ford MR,
    3. Warner GG,
    4. Watson S
    . MIRD Pamphlet No. 11: S, Absorbed Dose per Unit Cumulated Activity for Selected Radionuclides and Organs. Society of Nuclear Medicine and Molecular Imaging; 1975.
  78. 78.↵
    1. Bouchet LG,
    2. Bolch WE,
    3. Weber DA,
    4. Atkins HL,
    5. Poston JW Sr.
    MIRD pamphlet no. 15: radionuclide S values in a revised dosimetry model of the adult head and brain. Medical internal radiation dose. J Nucl Med. 1999;40:62S–101S.
    OpenUrlAbstract/FREE Full Text
  79. 79.↵
    1. Bolch WE,
    2. Bouchet LG,
    3. Robertson JS,
    4. et al
    . MIRD pamphlet no. 17: the dosimetry of nonuniform activity distributions—radionuclide S Values at the voxel level. J Nucl Med. 1999;40:11S–36S.
    OpenUrlAbstract/FREE Full Text
  80. 80.↵
    1. Rumiantcev M,
    2. Li WB,
    3. Lindner S,
    4. et al
    . Estimation of relative biological effectiveness of 225Ac compared to 177Lu during [225Ac]Ac-PSMA and [177Lu]Lu-PSMA radiopharmaceutical therapy using TOPAS/TOPAS-nBio/MEDRAS. EJNMMI Phys. 2023;10:53.
    OpenUrlPubMed
  81. 81.↵
    1. Sarrut D,
    2. Bardiès M,
    3. Boussion N,
    4. et al
    . A review of the use and potential of the GATE Monte Carlo simulation code for radiation therapy and dosimetry applications: GATE for dosimetry. Med Phys. 2014;41:064301.
    OpenUrlPubMed
  82. 82.↵
    1. Sgouros G,
    2. Hobbs RF,
    3. Abou DS
    . The role of preclinical models in radiopharmaceutical therapy. Am Soc Clin Oncol Educ Book. 2014:e121–e125.
  83. 83.↵
    1. Agostinelli S,
    2. Allison J,
    3. Amako K,
    4. et al
    . Geant4: a simulation toolkit. Nucl Instrum Methods Phys Res A. 2003;506:250–303.
    OpenUrlCrossRef
  84. 84.↵
    1. Arce P,
    2. Rato P,
    3. Canadas M,
    4. Lagares JI
    . GAMOS: a Geant4-based easy and flexible framework for nuclear medicine applications. In: 2008 IEEE Nuclear Science Symposium Conference Record. IEEE; 2008:3162–3168.
  85. 85.↵
    1. Hughes G
    . Recent developments in low-energy electron/photon transport for MCNP6. Prog Nucl Sci Technol. 2014;4:454–458.
    OpenUrl
  86. 86.↵
    MCNP 6.2 simulations of energy deposition in low-density volumes corresponding to unit-density volumes on the nanometre level. Radiat Meas. 2022;157:106831.
    OpenUrl
  87. 87.↵
    1. Battistoni G,
    2. Bauer J,
    3. Boehlen TT,
    4. et al
    . The FLUKA code: an accurate simulation tool for particle therapy. Front Oncol. 2016;6:116.
    OpenUrlPubMed
  88. 88.↵
    1. España S,
    2. Herraiz JL,
    3. Vicente E,
    4. Vaquero JJ,
    5. Desco M,
    6. Udias JM
    . PeneloPET, a Monte Carlo PET simulation tool based on PENELOPE: features and validation. Phys Med Biol. 2009;54:1723–1742.
    OpenUrlPubMed
  89. 89.↵
    1. Nuclear Energy Agency
    . PENELOPE-2018: A Code System for Monte Carlo Simulation of Electron and Photon Transport. OECD; 2019.
  90. 90.↵
    1. Zanzonico P
    . The MIRD schema for radiopharmaceutical dosimetry: a review. J Nucl Med Technol. 2024;52:74–85.
    OpenUrlAbstract/FREE Full Text
  91. 91.↵
    1. Besemer AE,
    2. Yang YM,
    3. Grudzinski JJ,
    4. Hall LT,
    5. Bednarz BP
    . Development and validation of RAPID: a patient-specific Monte Carlo three-dimensional internal dosimetry platform. Cancer Biother Radiopharm. 2018;33:155–165.
    OpenUrlCrossRefPubMed
  92. 92.↵
    1. Xiao Y,
    2. Roncali E,
    3. Hobbs R,
    4. et al
    . Toward individualized voxel-level dosimetry for radiopharmaceutical therapy. Int J Radiat Oncol Biol Phys. 2021;109:902–904.
    OpenUrlPubMed
  93. 93.↵
    1. Lassmann M,
    2. Eberlein U,
    3. Gear J,
    4. Konijnenberg M,
    5. Kunikowska J
    . Dosimetry for radiopharmaceutical therapy: the European perspective. J Nucl Med. 2021;62(suppl 3):73S–79S.
    OpenUrl
  94. 94.
    1. Strigari L,
    2. Caivano R,
    3. Avanzo M,
    4. et al
    . Twenty years of radiobiology in clinical practice: the Italian contribution. Tumori. 2014;100:625–635.
    OpenUrlPubMed
  95. 95.↵
    1. Pouget J-P,
    2. Santoro L,
    3. Piron B,
    4. et al
    . From the target cell theory to a more integrated view of radiobiology in targeted radionuclide therapy: the Montpellier group’s experience. Nucl Med Biol. 2022;104-105:53–64.
    OpenUrl
  96. 96.↵
    1. Bastiaannet R,
    2. Liatsou I,
    3. F Hobbs R,
    4. Sgouros G
    . Large-scale in vitro microdosimetry via live cell microscopy imaging: implications for radiosensitivity and RBE evaluations in alpha-emitter radiopharmaceutical therapy. J Transl Med. 2023;21:144.
    OpenUrlPubMed
  97. 97.↵
    1. Thacker BH,
    2. Doebling SW,
    3. Hemez FM,
    4. Anderson MC,
    5. Pepin JE,
    6. Rodriguez EA
    . Concepts of Model Verification and Validation. Los Alamos National Laboratory; 2004.
  98. 98.↵
    1. Riedmaier S,
    2. Danquah B,
    3. Schick B,
    4. Diermeyer F
    . Unified framework and survey for model verification, validation and uncertainty quantification. Arch Comput Methods Eng. 2021;28:2655–2688.
    OpenUrl
  99. 99.↵
    1. Lassmann M,
    2. Chiesa C,
    3. Flux G,
    4. Bardiès M
    ; EANM Dosimetry Committee. EANM Dosimetry Committee guidance document: good practice of clinical dosimetry reporting. Eur J Nucl Med Mol Imaging. 2011;38:192–200.
    OpenUrlCrossRefPubMed
  100. 100.↵
    1. Lassmann M,
    2. Eberlein U,
    3. Tran-Gia J
    . Multicentre trials on standardised quantitative imaging and dosimetry for radionuclide therapies. Clin Oncol (R Coll Radiol). 2021;33:125–130.
    OpenUrlPubMed
  101. 101.↵
    1. Venkatesh KP,
    2. Brito G,
    3. Kamel Boulos MN
    . Health digital twins in life science and health care innovation. Annu Rev Pharmacol Toxicol. 2024;64:159–170.
    OpenUrlPubMed
  102. 102.
    1. Laubenbacher R,
    2. Mehrad B,
    3. Shmulevich I,
    4. Trayanova N
    . Digital twins in medicine. Nat Comput Sci. 2024;4:184–191.
    OpenUrlCrossRefPubMed
  103. 103.↵
    1. Katsoulakis E,
    2. Wang Q,
    3. Wu H,
    4. et al
    . Digital twins for health: a scoping review. NPJ Digit Med. 2024;7:77.
    OpenUrlPubMed
  104. 104.↵
    1. Wu C,
    2. Lorenzo G,
    3. Hormuth DA,
    4. et al
    . Integrating mechanism-based modeling with biomedical imaging to build practical digital twins for clinical oncology. Biophys Rev (Melville). 2022;3:021304.
    OpenUrlPubMed
  105. 105.↵
    1. Wu C,
    2. Jarrett AM,
    3. Zhou Z,
    4. et al
    . MRI-based digital models forecast patient-specific treatment responses to neoadjuvant chemotherapy in triple-negative breast cancer. Cancer Res. 2022;82:3394–3404.
    OpenUrlCrossRefPubMed
  106. 106.↵
    1. Jensen J,
    2. Deng J
    . Digital twins for radiation oncology. In: Companion Proceedings of the ACM Web Conference 2023. ACM; 2023:989–993.
  107. 107.↵
    1. Sumini M,
    2. Teodori F,
    3. Isolan L
    . Digital twins in dosimetry and radiotherapy, a survey and some applications. Radiat Phys Chem. 2024;218:111649.
    OpenUrl
  108. 108.↵
    1. Enderling H,
    2. Chaplain M AJ
    . Mathematical modeling of tumor growth and treatment. Curr Pharm Design. 2014;20:4934–4940.
  109. 109.↵
    1. Anderson ARA,
    2. Chaplain MAJ,
    3. Newman EL,
    4. Steele RJC,
    5. Thompson AM
    . Mathematical modelling of tumour invasion and metastasis. Comput Math Methods Med. 2000;2:129–154.
    OpenUrl
  110. 110.↵
    1. Wang Z,
    2. Butner JD,
    3. Kerketta R,
    4. Cristini V,
    5. Deisboeck TS
    . Simulating cancer growth with multiscale agent-based modeling. Semin Cancer Biol. 2015;30:70–78.
    OpenUrlCrossRefPubMed
  111. 111.↵
    1. Baar M,
    2. Coquille L,
    3. Mayer H,
    4. et al
    . A stochastic model for immunotherapy of cancer. Sci Rep. 2016;6:24169.
    OpenUrlPubMed
  112. 112.↵
    1. Gatenby RA,
    2. Brown JS
    . Integrating evolutionary dynamics into cancer therapy. Nat Rev Clin Oncol. 2020;17:675–686.
    OpenUrlCrossRefPubMed
  113. 113.↵
    1. Li X,
    2. Zhao L,
    3. Zhang L,
    4. et al
    . Artificial general intelligence for medical imaging analysis. arXiv website. https://arxiv.org/abs/2306.05480. Published June 8, 2023. Revised November 21, 2024. Accessed February 4, 2025.
  114. 114.↵
    1. Moor M,
    2. Banerjee O,
    3. Abad ZSH,
    4. et al
    . Foundation models for generalist medical artificial intelligence. Nature. 2023;616:259–265.
    OpenUrlCrossRefPubMed
  115. 115.↵
    1. Weiss K,
    2. Khoshgoftaar TM,
    3. Wang D
    . A survey of transfer learning. J Big Data. 2016;3:9.
    OpenUrlCrossRef
  116. 116.↵
    1. Riether C,
    2. Schürch C,
    3. Ochsenbein A
    . From “magic bullets” to specific cancer immunotherapy. Swiss Med Wkly. 2013;143:w13734.
  117. 117.↵
    1. Basanta D,
    2. Gatenby RA,
    3. Anderson ARA
    . Exploiting evolution to treat drug resistance: combination therapy and the double bind. Mol Pharm. 2012;9:914–921.
    OpenUrlCrossRefPubMed
  118. 118.↵
    1. Fairman K,
    2. Choi M-K,
    3. Gonnabathula P,
    4. et al
    . An overview of physiologically-based pharmacokinetic models for forensic science. Toxics. 2023;11:126.
    OpenUrlPubMed
  119. 119.↵
    1. Fani M,
    2. Peitl P,
    3. Velikyan I
    . Current status of radiopharmaceuticals for the theranostics of neuroendocrine neoplasms. Pharmaceuticals. 2017;10:30.
    OpenUrlPubMed
  120. 120.↵
    1. Currie GM,
    2. Rohren EM
    . Radiation dosimetry, artificial intelligence and digital twins: old dog, new tricks. Semin Nucl Med. 2023;53:457–466.
    OpenUrlPubMed
  121. 121.↵
    1. O’Donoghue J,
    2. Zanzonico P,
    3. Humm J,
    4. Kesner A
    . Dosimetry in radiopharmaceutical therapy. J Nucl Med. 2022;63:1467–1474.
    OpenUrlAbstract/FREE Full Text
  122. 122.↵
    1. Lim DS,
    2. Jackson JD,
    3. Atala A,
    4. Yoo JJ
    . Leading approaches to vascularize kidney constructs in tissue engineering. Engineering. 2022;19:117–127.
    OpenUrlPubMed
  123. 123.↵
    1. Gameiro J,
    2. Marques F,
    3. Lopes JA
    . Long-term consequences of acute kidney injury: a narrative review. Clin Kidney J. 2021;14:789–804.
    OpenUrlPubMed
  124. 124.↵
    1. Fortuin A,
    2. De Rooij M,
    3. Zamecnik P,
    4. Haberkorn U,
    5. Barentsz J
    . Molecular and functional imaging for detection of lymph node metastases in prostate cancer. Int J Mol Sci. 2013;14:13842–13875.
    OpenUrlPubMed
  125. 125.↵
    1. Vargas CS,
    2. Struelens L,
    3. D’Huyvetter M,
    4. Caveliers V,
    5. Covens P
    . A realistic multiregion mouse kidney dosimetry model to support the preclinical evaluation of potential nephrotoxicity of radiopharmaceutical therapy. J Nucl Med. 2023;64:493–499.
    OpenUrlAbstract/FREE Full Text
  • Received for publication April 22, 2024.
  • Accepted for publication January 27, 2025.
Back to top

In this issue

Print
Download PDF
Article Alerts
Email Article
Citation Tools
Bookmark this article

Jump to section

Keywords