Abstract
242389
Introduction: A key PET system performance measurement is the noise equivalent count (NEC) rate vs. activity in a phantom, measured with high activity that decays. This measurement provides both the peak performance of the system and the activity at which that occurs. Neither metric can be assessed directly in patients. A method to predict NEC vs. activity based on a single scan and a simple dead-time model has been previously proposed [Stearns, 2003]. We have adapted that model to work on three different PET/CT systems, challenged by two long phantoms, one very small and one very large.
Methods: Three PET/CT scanners were used: GE Discovery 690 (D690), Discovery IQ (5-ring, DIQ), and Discovery MI (5-ring, DMI). These systems represent both BGO and LYSO, PMT and SiPM technologies and different block sizes, all of which affect count rate performance and background levels. One phantom was a 36 cm x 21 cm oval, 40 cm long (25 L) whole-body (WB) phantom around the size of a medium-large-sized patient. The other phantom was a 10.2 cm diameter, 41 cm long (3.15 L) PVC pipe phantom.
The WB phantom was filled with a large amount of radioactivity (~20 mCi) and was scanned repeatedly on the D690, DIQ, and DMI for ~16 hrs as it decayed. The PVC phantom was also filled with a large amount of radioactivity (~12 mCi for the D690 & DIQ, and ~17 mCi for the DMI) and was scanned for at least 11 hrs. The goal was to exceed the NEC peak for each system and produce NEC vs. activity curves over a wide range of activities.
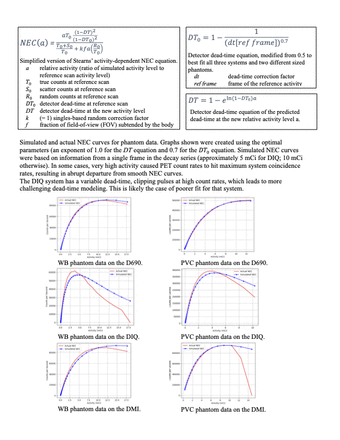
An initial evaluation of Stearns’ NEC model and using the dead-time data provided in the image header turned out to deviate from actual measurements. Slight adjustments were made to the dead-time scaling vs. activity to create a best-fit to the phantom data, considering the three different scanners and two phantom sizes. A more general expression for NEC vs. activity was developed that allowed two new exponent variables. To determine the optimal fit, both phantom sizes on all three systems were tested with a range of exponents, and the exponent that generated the lowest root mean square error for each of the six combinations was found. These exponents were averaged.
NEC was analyzed quantitatively using the NEC curve. Data including prompt and random counts, scan duration, activity, uptake time, scatter fraction, and dead-time correction factor were taken from the DICOM header using a Linux script. These data were graphed with a Python script to create NEC curves. The curves for each dataset were plotted vs. activity to compare how the different scanners and phantom sizes behaved for a range of activities.
Results: Different PET systems perform differently for the same activity levels. This claim is supported when comparing the different NEC curves between PET systems (shown in the supplemental material). For example, for the simulated PVC phantom data, image quality peaks at around 12.5 mCi on the D690 whereas it peaks at around 3.5 mCi on the DIQ and 9 mCi on the DMI.
It is also shown that these NEC curves peak at different activity levels for the different phantom sizes when looking at the same scanner. For example, for the simulated phantom data on the D690, image quality peaks at around 14 mCi for the WB phantom as opposed to 12.5 mCi for the PVC phantom.
The exponential parameter of the relative dead-time model (DT) from Stearns’ work produced the most accurate NEC curves when it was unchanged (1.0). The exponential parameter of the measured dead-time model (DT_0) in the denominator was changed from 0.5 to 0.7 to best fit the simulated data.
Conclusions: The newly-adjusted formula appears to accurately predict NEC rate over a wide activity range from a single scan for these PET systems scanners and phantom sizes. As expected, max NEC and peak activity vary considerably with phantom size and scanner. This process works well enough over a range of body sizes to pursue the optimization of patient doses.
In this issue
Jump to section
Related Articles
Cited By...
- No citing articles found.