Leveraging Counterfactual Generative Diffusion Probabilistic Model for Anomaly Detection: Application to Lung Cancer PET Images

Introduction: Minimizing the need for voxel-level annotated data for training PET image segmentation networks is crucial, particularly due to time and cost constraints related to expert annotations. Diffusion models are the current state-of-the-art for generative AI, which are primarily trained in an unsupervised/weakly-supervised manner, thereby reducing the need for annotations.

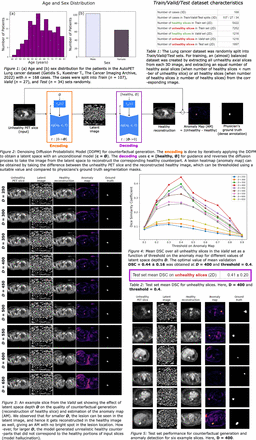
In this work, a Denoising Diffusion Probabilistic Model (DDPM) was trained with slice-level labels: unhealthy (with lesions) vs. healthy (without lesions) slices. During inference, the model was used to generate counterfactuals for unhealthy slices to obtain corresponding lesion-free slices. The anomaly map (AM) showing lesions was computed from the difference between the unhealthy and generated healthy slices.

Methods: In the forward process, inputs were normalized in (0,1) and were iteratively noised via Gaussian noise for 1000 timesteps. In the backward process, DDPM was implemented via a conditional denoising UNet which allowed controlling the synthesis process via labels c = {healthy, unhealthy}. Once the model was trained, the samples x were generated starting from noise by iteratively sampling from the reverse process via a Denoising Diffusion Implicit Model, mapping latent space to images.

During training, we employed implicit guidance by training DDPM on unconditional and conditional objectives via randomly dropping c (with 15% probability). For class conditioning, the underlying UNet was augmented with conditional attention mechanics where c was encoded (via embedding layers) and separately projected and concatenated to the attention context at each layer.

We used the lung cancer PET data obtained from the AutoPET challenge 2023. The 3D dataset was split into Train (n=107), Valid (n=27), and Test (n=34) sets. From cases in Train/Valid sets, all the unhealthy slices and an equal number of randomly sampled healthy slices were extracted along the axial direction to create a balanced 2D training dataset. For cases with more unhealthy slices than healthy, all the healthy slices were included in the Train/Valid set. All slices were centrally cropped, resampled (64x64) and normalized.

The input was encoded into a spatial latent space within an unconditional model c=∅. The counterfactual was generated by decoding the latent image while applying an intervention using c = healthy. The difference between the unhealthy input and the generated healthy image gave the AM which was used to recover lesions. The AM was normalized and thresholded using T. During inference on the Valid set, the number of time steps was fixed to 1000 and the latent space depth D was varied from 250 to 650 (stepsize=50). For each D, the mean DSC was computed between the unhealthy GT and thresholded AM for each value of T from 0.1 to 0.9 (stepsize=0.1). Hence, the best value of hyperparameters D and T were chosen on the Valid set for further analyses on Test set.

Results: The best hyperparameters were D=400 and T=0.4 obtaining a DSC = 0.44 ± 0.16 on the unhealthy slices in the Valid set (Fig. 4). We observed that for smaller D, the lesion can be seen in the latent image, and hence it gets reconstructed in the healthy image as well, giving an AM with no bright spot in the lesion location. However, for larger D, the model generated unrealistic healthy counterparts that did not correspond to the healthy portions of input slices (model hallucination; Fig. 3), again resulting in AMs with high uptake in unrealistic locations not overlapping the lesions in the GT mask. As a result, the optimal performance was found for an intermediate D = 400. With the same hyperparameters on the Test set, we obtained a DSC = 0.41 ± 0.20 (Fig. 5 and Table 2).

Conclusions: The anomaly detection model obtained meaningful generalization on the Test set. Ongoing work focuses on 3D models that directly process 3D images with class conditioning on different cancer phenotypes including extensive comparisons with other state-of-the-art techniques.

• Download figure
• Open in new tab
• Download powerpoint