Abstract
P1449
Introduction: To demonstrate the use of Cluster Gauss Newton (CGN) in pharmacokinetic models for radiopharmaceutical theranostics. Traditionally, parameter estimation problems have been expressed as nonlinear least square problems and solved iteratively. This approach, however, leads to local minimizers that are sensitive to initial iteration, while other proposed methods such as multi-start and derivative-free methods are computationally costly. By contrast, CGN is more computationally efficient and robust against local minima given its use of global linear approximations instead of Jacobians, and simultaneous solution of the nonlinear least squares problem from multiple initial iterations. As such, CGN is more likely to find approximate minimizers with a smaller sum of squared residuals (SSR).
Methods: Our physiologically based pharmacokinetic (PBPK) model for radiopharmaceutical delivery is modularly broken down into models for different organs and tumors. For organs and tumors with receptor binding, we utilize a 3-tissue compartmental model (Figure 1), modeling the radiopharmaceutical pathway from blood to interstitial space to receptor binding to cell internalization and release, including 6 parameters (K1, K2,K3,K4,λintern,λrelease). In this work, prostate-specific membrane antigen (PSMA) targeting radiopharmaceutical concentrations were simulated including statistical variations due to noise. Observation times were for up to 500 minutes (which can be achieved for F-18 for long axial field-of-view PET scanners, or for longer living radioisotopes such as Cu-64 and Tb-152). As shown in Figure 4, longer observations improve estimations, particularly for λinternand λrelease estimation. Longer observations result in more initializations reaching local minima with smaller SSRs. Based on prior knowledge defined by domain experts, an initial set of parameters were randomly generated within a range. For this study, the CGN parameters were set as N=250 (number of initializations; same as cluster number; i.e. number of points that cross-communicate), λ=1 (initial value of the regularization), γ=2 (strength of the weights) and Kmax (maximum number of iterations). Our last step is to pick the initialization that ends up with the lowest SSR amongst all cluster points. We performed a 20-time run of the algorithm on 20 different noise realizations, followed by analysis of bias and variance.
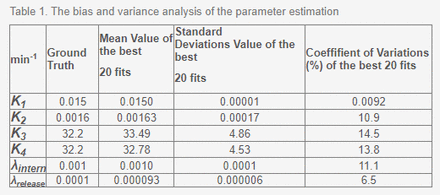
Results: A box plot of the initial cluster and the final cluster is shown in Figure 2. For K1, all points within the initial cluster achieved the smallest SSR (global minimizer), while the initial cluster spreads exhibited clear reductions for the other parameters. To reach local minimizers, CGN was used to estimate parameters from the initial cluster (Figure 3). Based on the best fit of CGN for 20 different runs, Table 1 summarizes the variance and bias analyses. According to the analysis, the mean values of the parameters have a maximum relative error of 7.0%, and the maximum coefficient variation is 14.5%. CGN reasonably estimated the parameters as a result of the analysis.
Table 1. The bias and variance analysis of the parameter estimation
Conclusions: PBPK models typically consist of stiff, ordinary differential equations with multiple parameters. In practice, many pharmacokinetic inverse problems are ill-posed and there are insufficient observations. For estimating parameters, CGN promises itself as an efficient method to overcome conventional nonlinear least square approaches.
In this issue
Jump to section
Related Articles
Cited By...
- No citing articles found.