Abstract
P1433
Introduction: Yttrium-90 (90Y) radioembolization is a minimally invasive technique to treat primary liver tumors, in which radioactive microspheres are injected into the hepatic artery to reach the tumor. For treatment planning, technetium-99 (99mTc) macroaggregated albumin (MAA) particles are previously injected and assumed to have a similar final distribution in the liver as 90Y microspheres. Our goal is to introduce a novel stochastic method to simulate the final distribution of different microspheres used in these treatments, based on liver-specific vasculature.
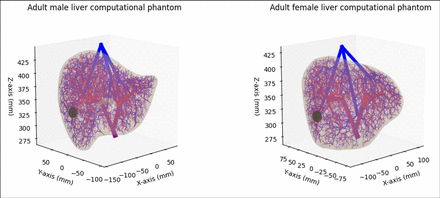
Methods: Adult male and female liver computational phantoms were implemented to include very detailed hepatic arterial, hepatic portal venous, and hepatic venous vasculature trees. Two spherical tumors of 20 mm diameter were arbitrarily placed in both models in the liver’s sixth segment based on the Couinaud classification (Figure 1). A tumor-scaling-specific parameter, α, was employed to transform the number of vessels entering the tumor in our vasculature model, V0, into the real number of vessels in the tumor accessible for microspheres, V = αV0. Three types of particles were simulated: 90Y glass (TheraSphere®), 90Y resin (SIR-Sphere®), and 99mTc–MAA. For each one of them, a Gaussian distribution of sizes was assumed according to the literature: 20-30, 20-60, and 10-90 microns, respectively. In each simulation, a user-definable number of microspheres were injected into the arterial branch of the sixth liver segment. Microspheres’ perfusion was simulated following a discrete Markov Chain, assigning probabilities to bifurcate according to Poiseuille’s and Murray’s Law or being stuck in the non-modeled capillaries branching out of each vessel, until reaching the tumor boundaries. Normal vessels were clogged whenever the particle size was bigger than the vessel size. Once at the tumor border, microspheres were stochastically lodged into the tumor according to a given probability, proportional to the number of vessels not-embolized in the tumor. In turn, microspheres entering the tumor may embolize its vessels as to a probability proportional to the cross-section of the microsphere, (Rm/Rv)2, being Rmthe radius of the microspheres and Rv the effective radius of the tumor vessels. Additionally, accumulated microspheres can jointly embolize vessels, so the resulting probability for vessel embolization also depends on the total number of microspheres (N) lodged into the tumor at a given point: (Rm/Rv)2 × [1-exp(-βN/α)], where β is a constant affecting the rate at which accumulated microspheres embolize vessels. The impact of the microsphere type and size on tumor filling was studied by simulating the injection of 600 000 microspheres for different values of the tumor-specific α and Rv parameters. For convenience, β was set at 0.01, meaning that, for every 100α microspheres the probability of embolizing a tumor vessel increases by 63%.
Results: Increasing the effective radius of the tumor vessels (Rv) while fixing the tumor-scaling parameter α, or increasing α while fixing Rv, lead to more microspheres in the tumor (Figure 2). Regardless α and Rv, larger microspheres (99mTc-MAA) tend to quickly embolize tumor vessels so fewer of them are needed to completely fill the tumor. On the other hand, a greater number of smaller microspheres (90Y) can be lodged in the tumor vessels.
Conclusions: This work shows the preliminary results of our novel stochastic method to investigate how microspheres perfuse through the liver vasculature. Our preliminary data show the ability of this method to cover different types and sizes of particles, as well as to consider tumor-specific scenarios. Of note, this model only considers the dynamics of tumor vessel embolization but disregards other aspects to be included in future versions, such as capillaries filling dynamic or tumor shunts. Lastly, for the determination and validation of the tumor-specific parameters of our model, patient-specific SPECT imaging will be considered.