Abstract
2431
Introduction: 18F-FDG-PET is sensitive to malignant tumors because it reflects increased uptake of glucose by tumour cells. The two-tissue compartment kinetic model parameters (K1, ml/g/min; k2, k3, 1/min; Ki=K1k3/(k2+k3), ml/g/min), introduced by Sokoloff et al., along with the cerebral metabolic rate of glucose derived from Ki, can contribute to the diagnosis and grading of brain tumours. The conventional approach in kinetic modelling is to extract kinetic parameters by fitting the kinetic model to the Time Activity Curve (TAC) using Non-Linear Least Squares (NLLS). In brain tumours, k3 and Ki are expected to be large. In this case, the TAC becomes less sensitive to k3 since the TAC only changes slightly with relatively large k3 changes. It then becomes difficult to estimate k3 accurately, especially when the TAC is noisy. A similar situation arises when k3 is small relative to k2 (i.e., low uptake). Both conditions are known to cause over-or under-estimation of kinetic parameters. Instead of just using the two-tissue compartment model, we consider the use of additional, simplified models, to aid in estimating kinetic parameters accurately. A machine learning model selection framework was used to first estimate kinetic model parameters, after which an assessment of which model better explains tracer kinetics was made.
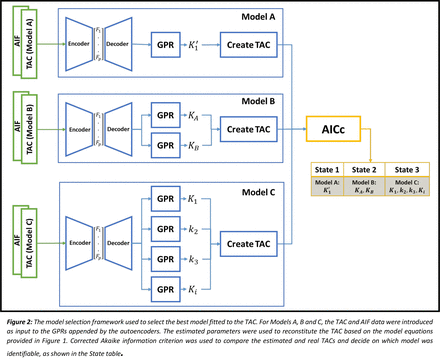
Methods: Three model configurations (Models A, B and C) were evaluated in terms of their ability to describe tissue kinetics. Figure 1 provides the model configurations; Models A and B are simplifications of Model C, assuming k3 >> k2 and k3 << k2 in the two-tissue compartment model, respectively. Figure 2 depicts the model selection technique. Gaussian Process Regression (GPR) appended by an autoencoder was employed to build the machine learning kinetic modelling framework. Individual TACs were simulated using an in-house simulation environment developed in MATLAB®, with Gaussian noise level set at c=0.1. Training consisted of 2,200 TACs, and testing was performed using 100 TACs for each k3 - k2 ratio. Each TAC was simulated using the two-tissue compartment model. Parameters K1, k2 and k3 were set using a pseudo-random number generator pulled from a (0, 1] uniform distribution constrained to k3 - k2 ratio ranges of 0-0.01, 0.01-0.1, 0.1-0.3, 0.3-0.5, 0.5-1.0, 1.0-2.0, 2.0-10, 10-100. GPRs for all three models were applied to the simulated TACs, and K'1, KA and KB, and K1, k2 and k3 (provided in Figure 2) were estimated using the corresponding models. The most parsimonious model was chosen using the corrected Akaike Information Criterion (AICc), and the computed R2 values for each of the parameters were used to assess the goodness-of-fit of each model.
Results: Figure 3 provides the model selection results with R2 values corresponding with each of the k3 - k2 ratio ranges evaluated. The table highlights that when model selection is not used, the values for k2 and k3 can be difficult to capture accurately for certain k3 - k2 ratios. In particular, R2 values are low when k3 > 2k2 and k3 < 0.01k2. For these cases, Models A and B are preferred, respectively. Parameters k2 and k3 in the standard two-tissue compartment model can be estimated accurately in the 0.01-1.0 k3 - k2 ratio range. The accuracy of kinetic model parameters generally improves with model selection. It should be noted that model selection provides an opportunity to identify and avoid k2 and k3 estimates in settings that may result in large errors (see summary plots in Figure 3).
Conclusions: In the case of blood-brain-barrier damage, k2 may be quite large, and similarly, k3 is likely large for brain tumour regions. In these two clinically relevant settings, model identifiability may play an important role in determining the accuracy of parameter estimates.
In this issue
Jump to section
Related Articles
Cited By...
- No citing articles found.