RADAR Guide: Standard Methods for Calculating Radiation Doses for Radiopharmaceuticals, Part 1—Collection of Data for Radiopharmaceutical Dosimetry

FDA REQUIREMENTS FOR RADIOPHARMACEUTICAL DOSIMETRY

The FDA expects that preclinical studies will be used to determine dosimetry in animals and that human dosimetry needs to be determined as part of phase 1, 2, and 3 studies. The FDA sets standards for the use of lasers (title 21 of Code of Federal Regulations) and other nonionizing radiation, food irradiation, and pharmaceuticals. Medical imaging agents are submitted for approval in investigational new drug applications, new drug applications, biologics license applications, abbreviated new drug applications, and supplements to new drug applications or biologics license applications.

The radiation safety assessment that is associated with the approval of use of medical imaging agents includes many requirements for dose calculations to support these submissions (3). Applicants should provide a description of which organs have a significant accumulation of activity over time, what activity levels were observed at different times (with at least 2 time points obtained per phase of radionuclide uptake or clearance), an evaluation of time integrals of activity, descriptions of how they were obtained, and a description of how they were combined with dose conversion factors to obtain doses (if not done by software). Any significant radiation hazards to other patients and health-care workers should also be assessed.

FDA requirements (4) require a preclinical phase, in which studies are done on an animal species, and phase 1, 2, and 3 clinical studies, in which dosimetry data are gathered from human subjects, to establish and refine the radiation dose estimates and establish the safety and efficacy of any new drug.

First-in-humans studies can establish the safety and tolerability and preliminary efficacy of a new drug before entering into full-fledged clinical trials, but all 4 phases of study are needed to establish the radiation dosimetry of any candidate for a new drug application (5).

PLANNING A STUDY TO OBTAIN BIOKINETIC DATA

In either animal or human studies, one must collect sufficient data to fully characterize the radiation dose (Gy) to all relevant organs and tissues in the body. Siegel et al. (1) noted that there are 5 key questions in study design: what regions are source regions, how fast the radioactivity accumulates in these source regions, how long the activity remains in the source regions, how fast the activity is excreted from the source organs, and how much activity is in the source regions as a function of time after administration.

A starting point in considering study design is the physical half-life of the radionuclide used. Gathering data over several half-lives should give a good evaluation of the complete decay of the compound in the body. A very short-lived nuclide such as ¹¹C (which has a 20-min physical half-life) does not afford a long time for gathering image data. Furthermore, one must consider the radiopharmaceutical’s effective half-time (although usage varies, the term half-life is generally used for physical half-lives, whereas half-time is generally used for biologic and effective half-times): Eq. 1 where T_e is the effective half-time, T_p is the radionuclide’s physical half-life, and T_b is the compound’s biologic half-time (the time for half the activity in a region to be cleared by biologic elimination). Physical decay and biologic clearance work in parallel to remove radioactivity more quickly overall than either one would alone. For example, because ^99mTc has a 6-h T_p, one might think of gathering data over 24–48 h. However, because ^99mTc-DTPA is cleared by the kidneys in just a few short minutes and is cleared from the body overall with about a 1.7-h biologic half-time (6), 3–10 effective half-times would be 4–13 h, and many data points would need to be gathered in a relatively short time after administration. A more slowly cleared ^99mTc compound could be imaged over longer times. A compound labeled with ¹³¹I (T_p = 8 d) and whose clearance is relatively slow could possibly be sampled with a few data points on the first day and then one data point per day for several days. Study design is not an exact science, but care must be taken not to undersample the data when there may be several phases of uptake and clearance. Some radiopharmaceuticals (e.g., ¹³¹I tositumomab; Bexxar [GlaxoSmithKline]) are well characterized by a single exponential decay function for the whole body, whereas others may have 2 distinct phases of clearance—an early phase that is dominated by rapid clearance of a portion of the administered activity and a later phase that is dominated by slower clearance of the remainder of the administered activity. Of course, physical decay is superimposed on these biologic clearance processes. Although it is common for most uptake in organs to be fairly rapid, some organs, tissues, and tumors may exhibit an exponential phase of uptake and one or more phases of clearance. In any case, it is important to capture the early peak uptake and rapid washout phase, covering at least 3–5 effective half-times (T_e) of the radiopharmaceutical. Report 67 of the International Commission on Radiation Units and Measurements (7) suggests that data points typically be taken near ⅓, ⅔, 1½, 3, and 5 times the T_e; be collected from at least 2 time points during the interval in which each biologic clearance phase is dominant; account for 100% of the activity at all times; and account for all major paths of excretion (e.g., urine, feces, and exhalation).

Clinical application of these requirements can be difficult. For longer-lived radionuclides such as ¹³¹I and ¹⁷⁷Lu, capturing the behavior of early and late clearance phases may require obtaining multiple data points on the first day, then one data point each day for several days afterward. Obtaining these at times when clinical staff are available and patients can return may present logistic challenges. Siegel et al. (1) analyzed the error that can occur if the uptake and washout phases of clearance are not adequately sampled. For example, Figure D2 of their article (Fig. 1) shows the variation of t_max (the time for initial sampling) that constrains the error to a given percentage, as a function of effective washout half-time (T_e) for 4 different values of percentage error (<10%) in estimates of an organ’s area under the curve (i.e., the time-integrated activity).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 1.

Variation in t_max to constrain error on area under curve to fixed percent. (Reprinted from (1).)

Madsen et al. demonstrated that when the effective half-time of a monoexponentially clearing radiopharmaceutical is fairly consistent among patients, the time-integrated activity may be estimated by taking a single measurement at the mean lifetime (i.e., 1.443 times the effective half-time) of the radiopharmaceutical. In the case of a biexponential clearance, the effective half-time of the longer-lived component should be used. Although most of the resulting renal dose estimates in a clinical study of 47 patients who were administered ⁹⁰Y-DOTATOC were within 10% of those based on multiple-time-point imaging, some differed by as much as 22%. The investigators suggest that the population effective half-time may be obtained from a clinical study or from pharmacokinetic modeling. This approach might not be sufficiently accurate, though, when there is a wide variation among patients or even among the source organs within individuals.

Stabin (8) provided a more comprehensive analysis of the influence of all parameter values on the overall uncertainty in internal dose estimates.

EXTRAPOLATING ANIMAL DATA TO HUMANS

In an animal study, the compound under study may be administered to several animals, which are then sacrificed at different times, with the activity within the organs estimated by counting (harvesting the organs and counting them in a well counter or other device), or perhaps using autoradiography techniques or imaging of the animals (e.g., with a small-animal PET or small-animal SPECT imaging system). Serial imaging with microimaging systems obviates killing of animals but may complicate the interpretation of the kinetic data that are obtained, as the animals generally need to be anesthetized, which may alter their physiologic state.

The data gathered are then used to predict uptake values in humans from the concentrations seen in animal tissues (extrapolation). Extrapolation of animal data to humans is by no means an exact science. Crawford and Richmond (9) and Wegst (10) studied some of the strengths and weaknesses of various extrapolation methods that have been proposed in the literature. One method of extrapolating animal data that has been widely applied is the % kg/g method (11). Considering %/organ or %/g in an animal to be the same as %/organ or %/g in humans is subject to certain pitfalls. In the % g/kg method, the animal organ data need to be reported as percentage injected activity per gram of tissue, and this information plus knowledge of the animal whole-body weight is used in the following extrapolation: 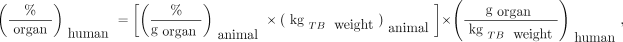Eq. 2 where % is percentage administered activity, g_organ is the mass of the organ in grams, and kg_TBweight is the mass of the whole animal in kilograms. Table 1 shows example calculations of data extrapolated from an animal species to humans using this approach (12). The animal whole-body weight was 20 g (0.02 kg), and the human source organ chosen had a mass of around 300 g. The human total-body weight for the standard adult male of 70 kg was used in the calculations. For example: 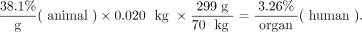Eq. 3

Some researchers have also suggested a transformation of the time scale, to account for the differences in metabolic rate among species of different body mass, based on the idea that faster metabolic rates will result in faster clearance of compounds from the body. One suggested scaling approach is given as follows: 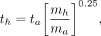Eq. 4 where t_a is the time at which a measurement was made in an animal system, t_h is the corresponding time assumed for the human data, and m_a and m_h are the total-body masses of the animal species and of humans, respectively. Table 2 shows an example with data extrapolated from an animal species to humans using this time-scaling approach (10). In this example, the animal whole-body weight was 200 g (0.2 g), and again, the human total-body weight for the standard adult male of 70 kg was used in the calculations. For example: 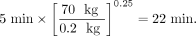Eq. 5

One problem in the area of animal data extrapolation to humans is the treatment of activity that is not accounted for in individual animal organs. Some researchers manage to successfully account for activity in the carcass, or the rest of the animal body that was not harvested for counting. If the radionuclide is particularly short-lived, this assessment may not be necessary, as one may be able to simply assume that activity unaccounted for was uniformly distributed in other tissues and eliminated only by radioactive decay. For many radiopharmaceuticals, this assumption may significantly overestimate the number of disintegrations in these remainder tissues and underestimate the number of disintegrations in excretory organs such as the urinary bladder and the intestines. An assessment of the activity in these regions, via direct counting or analysis of excreta, is usually needed. Such values are usually not extrapolated to humans on a mass basis but are assumed to apply directly (i.e., % excreted by the animal = % excreted by the human); a time extrapolation may be applied if desired. Gathering of excreta data is quite important to accounting for 100% of the administered activity. If it is known that all excretion is urinary, one can use (100% minus the total-body retention) as the excreted fraction. If both urinary and intestinal excretion are possible, the collection of both urinary and fecal data is needed.

Sparks and Aydogan (13) investigated the accuracy of animal data extrapolation to humans for several radiopharmaceuticals. They reached no solid conclusions that any particular method was superior to another. They did find, however, that extrapolated animal data tend to underestimate human organ self-doses. Figure 2, adapted from Figures 1 and 4 in their publication, show 2 examples of their results. These figures show the ratio of organ residence times (normalized number of disintegrations), which is also proportional to organ self-dose, when no extrapolation was performed (their Fig. 1) or both the time and the mass extrapolations shown above (their Fig. 4) were performed. A ratio of 1.0 represents perfect agreement, whereas ratios below 1.0 imply that the animal data underpredicted human doses, and ratios above 1.0 imply overestimation of human doses. One would like to see a normal distribution centered around 1.0. The graphs might fit a lognormal distribution, but nonetheless, in most cases, extrapolated animal data underpredicted human doses. Thus, providing dosimetry data to the FDA in preclinical studies is necessary in the drug approval process, but in most cases, reasonably accurate human doses will be derived only from the phase 1, 2, and 3 clinical studies on humans.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 2.

Frequency distribution of ratio of organ residence times using raw data or time and mass data extrapolated from animals to humans. (Adapted from (13).)

An important point in the elements of study design that are listed above is to account for 100% of the activity at all times. This is not always easy in preclinical studies, especially for organs that are distributed, such as the musculature and the skeleton, and for the whole body if the carcass of the animal after the removal of specific source organs is too large to be counted unless cut into numerous small pieces. The design of a preclinical study should include how this matter will be addressed, as it might well be too late to obtain this information after the performance of a study that neglects this point.

STEPS FOR COLLECTING DATA FROM HUMAN SUBJECTS

The external conjugate-view method, using anterior and posterior projection images from a nuclear medicine camera, is the method used most frequently used to obtain quantitative data in human studies for dosimetry. In this method, the source activity A_j is given as follows (1): 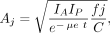Eq. 6 Eq. 7 where I_A and I_P are the observed counts over a given time for a given region of interest (ROI) in the anterior and posterior projections (counts/time); t is the average patient thickness over the ROI; μ_e is the effective linear attenuation coefficient for the radionuclide, camera, and collimator; C is the system calibration factor C (counts/time per unit activity); and the f is a correction for the source region attenuation coefficient (μ_j) and source thickness (t_j) (i.e., source self-attenuation correction). Figure 3 shows the geometric relationships. This expression (Eq. 6) assumes that the views are well collimated (i.e., they are oriented toward each other without offset) and also assumes a narrow-beam geometry without significant scattered radiation, septal penetration, or other interferences. Corrections for scatter are usually advisable; several proposed methods are described below.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 3.

Geometric representation of correction for attenuation in geometric mean method. t is total thickness of subject, whereas t₁ is depth of middle of source from upper surface and t₂ is depth of source from lower surface. t = t₁ + t₂. Product of upper and lower attenuation factors is dependent only on total thickness and not position of source within subject.

CORRECTIONS FOR SCATTERED RADIATION

One relatively straightforward correction procedure for scatter compensation is the triple-energy-window method (14); this involves establishing counting windows on either side of the γ-camera photopeak window such that the area of the 2 adjacent windows is equal to that of the photopeak (or if not, the count ratios should be appropriately scaled). The corrected photopeak counts (C_T) are given as follows: Eq. 8 where C_pp is the total count recorded within the photopeak window and C_LS and C_US are the counts within the lower and upper scatter windows, respectively. The scaling factor (F_S) corrects for the (most common) case in which the total width of the scatter windows (in keV) is not equal to that of the photopeak window. It would be unity if they were equal. Thus, adjustment of the adjacent windows is assumed to compensate for the high-energy-photon scatter tail on which the true photopeak events ride. Even if the areas of the scatter windows are equal to the area of the photopeak window, the use of a scaling factor other than unity may provide the best correction for scatter in a given system with a particular radionuclide. This correction may be determined by studying a source of known volume submerged to a realistic depth in a water phantom whose dimensions are similar to those of a human subject (Fig. 4). An extension of the triple-energy-window approach is to use more energy windows and to apply principal-component analysis or factor analysis to the resulting data in the energy dimension.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 4.

Example of use of multiple windows to correct for scattered radiation in γ-camera images. Ideal spectrum of ¹⁶⁶Ho is plotted in blue, and spectrum blurred by energy resolution of γ-camera is plotted in orange. Upper scatter window captures down-scatter from high-energy γ-rays, whereas lower scatter window captures down-scatter from 81-keV γ-ray as well. Weighting factor of 0.65 on lower scatter window was determined empirically. LS = lower scatter window; PP = photopeak; US = upper scatter window.

SPECT reconstruction methods have incorporated more sophisticated methods of scatter correction such as estimating the point-spread function of the scattering and applying it during the forward projection of data in an iterative reconstruction algorithm such as maximum-likelihood expectation maximization.

Commercial SPECT/CT cameras and software have recently been introduced that offer quantitative SPECT in the same manner that PET is quantitative. They include calibrations for specific radionuclides with corrections for attenuation and scatter.

CORRECTIONS FOR BACKGROUND ACTIVITY

When an ROI is drawn over a source region on a projection image, some counts from the region will have originated from activity in the subject’s body that is outside the identified source region. This includes scattered radiation from other ROIs, background radiation, and other sources. Thus, a background ROI is drawn over some region of the body that is close to the source ROI and that, in the analyst’s opinion, best represents the activity of nearby tissues to the source that will provide the best estimate of a background count rate to be subtracted from the source ROI. As with the scatter correction shown above, a scaling factor may be needed to correct the number of counts in the background ROI so that the appropriate correction is made, given the number of pixels in the source and background ROI. Alternately, one may simply subtract the number of counts per pixel in the background ROI from the number of counts per pixel in the source ROI and then calculate the total number of counts in the source ROI as the corrected number of counts per pixel times the number of pixels.

One way to make a quality assurance check is to place a source of activity of the radionuclide being imaged external to the body. Then, an ROI is drawn away from the subject’s body and also away from any star-pattern streaks that may accompany the source image because of septal penetration, but close enough that it captures a typical number of counts per pixel that represents background and scattered radiation within the imaging area close to the subject. The counts of this source over time should reflect the radionuclide physical half-life.

It is important to avoid drawing a background ROI over body structures that may contain a high level of activity (e.g., blood vessels and areas of the skeleton with significant uptake), as this will remove too many counts from the source ROI. It is also important not to draw the background ROI too far away from the source region in an area of particularly low background, as this may not remove enough counts from the source ROI. The choosing of locations and sizes of background ROIs is difficult to prescribe exactly, and practices vary considerably among investigators, potentially resulting in markedly different results for the final estimates of activity assigned to a source ROI. This process should be performed with care and attention to the above points for the best and most reproducible results. The locations of the background ROIs should be documented, perhaps by graphical screen captures if necessary, to enhance the reproducibility of a dosimetric analysis.

Pereira et al. (15) showed examples of optimized background regions for regions in a water phantom representing organs of interest (Fig. 5), noting possible uncertainties in different quantification methods.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 5.

Background regions drawn by Pereira et al. in water phantom. Background region is positioned over area near source that has count density of object in absence of source. (Reprinted from (15).)

CORRECTION FOR OVERLAPPING ORGANS AND REGIONS

It is not uncommon for some organs or tumors to overlap other structures in projection images. The right kidney and the liver are frequently partially superimposed in such images, as are the left kidney and spleen, in many subjects. When organ overlap occurs, the total activity within a source can be estimated by various approximate methods. For paired organs, such as the kidneys and lungs, one approach is simply to quantify the activity in one of the organs for which there is no overlap with other organs and double the number of counts in this organ to obtain the total counts in both organs. If the masses of the paired organs can be determined, perhaps using volumes that are derived from CT or MR images, and are then multiplied by the tissue density, then the scaling factor could be the combined masses of the 2 organs divided by the mass of the organ without overlap. Another approach is to draw an ROI over the region of the organ that has no overlap in scans where there is overlap, count the number of pixels, note the average count rate per pixel, use an ROI from another image in which there is no apparent overlap and the whole organ is clearly visible, count the number of pixels in a larger ROI drawn on this image, and then simply multiply the count rate per pixel from the first image by the number of pixels in the second image in order to estimate the total counts from the organ in the first image. Or, equivalently, take the total number of counts in the partial-organ ROI in the first image and multiply by the ratio of the numbers of pixels in the ROIs in the second and the first images, respectively. If no image can be found in which a significant overlap with another organ does not obscure the organ boundaries, an approximate ROI may need to be drawn just from knowledge of the typical shapes of such organs. This kind of approximation is obviously not ideal, but it may be necessary.

OBTAINING γ-CAMERA SYSTEM ATTENUATION AND CALIBRATION COEFFICIENTS

System Calibration Factor

As with the attenuation coefficient, the system calibration factor, C, must be measured at some time before or after radiopharmaceutical administration in a separate experiment. For this factor, the method is to prepare a standard of known activity of the same radionuclide as that to be used for administration to subjects, usually a few tens of megabecquerels in almost any suitable container (e.g., a syringe or vial). The exact source strength is not important, as long as sufficient counts are obtained for a consistent evaluation over the course of the study and as long as not too many counts are obtained, resulting in count saturation and possibly dead time in the camera. The standard should be counted in air for a fixed time (e.g., 5 min) at a source-to-collimator distance that approximates that of the patient midline distance used for the imaging study (Fig. 6).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 6.

Use of point source to establish system calibration coefficient.

The count rate per unit activity (in units of, for example, cpm/Bq or cpm/µCi) represents the calibration factor. The collimator count-rate response as a function of the source-to-collimator distance must be known. For parallel-hole collimators, the collimator efficiency is invariant near the center of the field of view; however, for other collimators, such as diverging, converging, and pinhole collimators, the efficiency is dependent on the source-to-collimator distance. It is also important to use the same camera settings, such as the width of the energy window, for this calibration as for the patient imaging.

In most cases the self-attenuation factor f is not significantly different from unity and is rarely important. Normally, one assumes that the variation in body thickness across individual ROIs is small, and so a single attenuation factor may be used to calculate the activity for the entire ROI. On the other hand, if the ROI is large and body thickness is thought to vary substantially within the ROI, a pixel-by-pixel calculation may be made. A pixel-by-pixel attenuation calculation can always be made, regardless of this assumption. A conjugate-view measurement is thus made at each of the time points chosen and the best ROIs for each region are superimposed on the images at each time. Because of potentially different rates of uptake and clearance in various tissues, individual organs or tumors may be best visualized at different times after administration. Some regions have most of their uptake early and clear quickly, whereas others may accumulate activity more slowly. Thus, different times may be chosen at which to draw the best ROIs for different regions. The best approach is to have a computer program that allows the ROIs to be independently defined and saved but then linked together and moved together, to allow the relative locations of all ROIs to be retained when new ROIs are defined, or when different patient images reflect slightly different patient placement on the imaging table or slightly different patient orientation toward the camera heads. Care should be taken to have the patient recline in the same position in all images, as differences in patient orientation toward the camera heads may change the lateral separation between organs. One aid in achieving this consistency are the cushions that are used to stabilize the patient and produce reproducible positioning in radiation oncology.

USE OF TOMOGRAPHIC DATA IN QUANTITATIVE IMAGING

The use of tomographic data, either SPECT or PET, for quantitative image analysis for dosimetry overcomes some of the problems inherent in anterior–posterior planar imaging. The advent of hybrid SPECT/CT cameras enable improved attenuation correction, and iterative reconstruction techniques allow correction for scattering and for depth-dependent resolution. The first quantitative SPECT/CT systems for implementing voxel-based dosimetry are appearing commercially. Scatter and attenuation corrections are inherently applied in the image reconstruction process. An important problem in planar imaging is organ overlap. For example, the right kidney is usually partially or totally obscured by the liver. Tumors may also be difficult to delineate because of other overlying structures with significant activity. In the case of PET, routine calibrations for clinical diagnoses ensure that the data provided are already quantitative and can be used directly for dose calculations. In SPECT, clinical needs normally do not necessitate an absolute activity quantification. Performing quantitative SPECT for internal dose calculations is somewhat more difficult than is planar imaging, but for the reasons noted above, may offer desirable advantages. Dewaraja et al. (16) provided an overview of methods to perform quantitative SPECT for radionuclide therapy. The steps that they outlined were as follows: acquisition, dead-time corrections, image reconstruction, compensation for image-degrading effects (attenuation, scatter, and detector response), definition of targets, determination of the camera calibration factor, completion of partial volume corrections, and integration of the time–activity curves.

As SPECT image acquisition and quantification is more difficult and time-consuming than a planar image acquisition, and each CT scan for attenuation correction imparts an additional absorbed radiation dose to the patient, one may use a hybrid method—using a series of planar images to establish the overall biokinetic behavior, with one or more SPECT images taken concurrently with a planar image—to better establish absolute accuracies (Fig. 7).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 7.

Combining SPECT and planar images for activity quantification. Planar images are acquired at every time point, whereas quantitative SPECT/CT images are acquired at only one time point. Volume of interest containing source in SPECT images is then used to calibrate counts from same source in planar images.

At the time that this is being written, new technology both in PET and in SPECT is promising to improve the accuracy of dosimetric workups by enabling volumetric imaging. Two recently introduced commercial long-axial-extent PET systems might be characterized as whole body. One has a 2-m axial field of view, which can literally image the entire body of most patients at once. The other has a 106-cm axial field of view, which is designed to be able to image most patients from the crown of the head to the mid thigh. These systems have much higher sensitivity than more typical PET scanners and thus can acquire useful data over a longer portion of the time–activity curve, which should improve the estimation of the time-integrated activity. They also acquire the entire volume simultaneously, which again improves the time–activity curve.

Whole-body SPECT is available in preclinical instrumentation. That technology is reportedly being scaled up to accommodate adult humans. The novel SPECT technology that was originally developed for cardiac imaging acquires data from many points of view in such rapid succession that it is effectively simultaneous in 3 dimensions over the time scale of the physiologic processes of interest in internal dosimetry. That technology has been built into a full-ring SPECT camera with an axial field of view of roughly 60 cm. Although its cadmium-zinc-telluride detectors are better suited to low- and medium-energy radionuclides than to high-energy radionuclides, its higher sensitivity and better energy resolution allow SPECT scans of many radionuclides to be acquired in the time that an ordinary γ-camera requires for a planar whole-body scan.

DISCLOSURE

No potential conflict of interest relevant to this article was reported.