Abstract
82Rb cardiac PET allows the assessment of myocardial perfusion with a column generator in clinics that lack a cyclotron. There is evidence that the quantitation of myocardial blood flow (MBF) and coronary flow reserve (CFR) with dynamic 82Rb PET is feasible. The objectives of this study were to determine the accuracy and reproducibility of MBF estimates from dynamic 82Rb PET by using our methodology for generalized factor analysis (generalized factor analysis of dynamic sequences [GFADS]) and compartment analysis. Methods: Reproducibility was evaluated in 22 subjects undergoing dynamic rest and dipyridamole stress 82Rb PET studies at a 2-wk interval. The inter- and intraobserver variability of MBF quantitation with dynamic 82Rb PET was assessed with 4 repeated estimations by each of 4 observers. Accuracy was evaluated in 20 subjects undergoing dynamic rest and dipyridamole stress PET studies with 82Rb and 13N-ammonia, respectively. The left ventricular and right ventricular blood pool and left ventricular tissue time–activity curves were estimated by GFADS. MBF was estimated by fitting the blood pool and tissue time–activity curves to a 2-compartment kinetic model for 82Rb and to a 3-compartment model for 13N-ammonia. CFR was estimated as the ratio of peak MBF to baseline MBF. Results: The reproducibility of the MBF estimates in repeated 82Rb studies was very good at rest and during peak stress (R2= 0.935), as was the reproducibility of the CFR estimates (R2 = 0.841). The slope of the correlation line was very close to one for the estimation of MBF (0.986) and CFR (0.960) in repeated 82Rb studies. The intraobserver reliability was less than 3% for the estimation of MBF at rest and during peak stress as well as for the estimation of CFR. The interobserver reliabilities were 0.950 at rest and 0.975 at peak stress. The correlation between myocardial flow estimates obtained at rest and those obtained during peak stress in 82Rb and 13N-ammonia studies was very good (R2 = 0.857). Bland–Altman plots comparing CFR estimated with 82Rb and CFR estimated with 13N-ammonia revealed an underestimation of CFR with 82Rb compared with 13N-ammonia; the underestimation was within ±1.96 SD. Conclusion: MBF quantitation with GFADS and dynamic 82Rb PET demonstrated excellent reproducibility as well as intra- and interobserver reliability. The accuracy of the absolute quantitation of MBF with factor and compartment analyses and dynamic 82Rb PET was very good, compared with that achieved with 13N-ammonia, for MBF of up to 2.5 mL/g/min.
PET measures of myocardial blood flow (MBF) (in mL/min/g) and coronary vasodilator reserve are very sensitive for evaluating microvascular function in vivo (1–3). Although the quantitation of MBF with 13N-ammonia and 15O-water as PET flow tracers has been validated, these tracers are seldom used clinically because they are cyclotron products with short physical half-lives (10 and 2 min, respectively) and therefore require an on-site cyclotron. In contrast, 82Rb can be produced with a column generator; consequently, it is the agent most commonly used for assessing myocardial perfusion in patients with known or suspected coronary artery disease (CAD) (4–10). Although this approach has been shown to be highly accurate for the detection of obstructive CAD (11,12), it underestimates the extent of underlying CAD, especially in patients with multivessel disease. This limitation could be overcome by adding the quantification of MBF to routine visual or semiquantitative assessments of myocardial perfusion.
We and others have shown that the absolute quantitation of MBF and coronary flow reserve (CFR) with dynamic 82Rb PET is feasible in humans (7–10,13,14). However, little is known about the accuracy and reproducibility of this approach to estimating MBF. Accordingly, we sought to determine the reproducibility of MBF estimates with 82Rb PET as well as the intra- and interobserver reliability of these quantitative measures. In addition, we determined the accuracy of the quantitative 82Rb PET approach by comparing measures of MBF obtained with 82Rb and those obtained with 13N-ammonia.
MATERIALS AND METHODS
Study Population
Two separate groups of subjects were recruited for the reproducibility and accuracy studies. We included patients at risk for or with known CAD, defined by the presence of fixed or reversible perfusion defects on clinically indicated PET. We also included healthy volunteers with a low likelihood of obstructive CAD, on the basis of the absence of chest pain and coronary risk factors and a normal resting electrocardiogram. Subjects who were pregnant or breast-feeding were excluded, as were those with uncontrolled hypertension (>200/120 mm Hg), unstable coronary syndromes, significant cardiac arrhythmias, valvular heart disease, decompensated congestive heart failure, bronchospastic pulmonary disease, or known hypersensitivity to dipyridamole.
Study Design
The Institutional Review Board of Partners Healthcare System, Boston, MA, approved the study protocol, and all participants gave written informed consent. Each subject made 2 hospital visits (visits 1 and 2), during which rest and dipyridamole stress myocardial perfusion was assessed. In the reproducibility study, all subjects underwent rest and dipyridamole stress myocardial perfusion PET studies with 82Rb as the flow agent at a 2-wk interval. In the accuracy study, all subjects underwent separate rest and dipyridamole stress myocardial perfusion PET studies with 82Rb and 13N-ammonia, respectively, also at a 2-wk interval.
PET
All subjects refrained from using caffeine-containing beverages or theophylline-containing medications for 24 h before each PET scan. Vasoactive medications were withheld for 24 h before the study. All subjects were studied in the fasting state.
82Rb PET
All 82Rb studies were performed in the 2-dimensional mode with a whole-body PET/CT scanner (Discovery STE Lightspeed 64; GE Healthcare). Myocardial perfusion was assessed at rest and during vasodilator stress with dipyridamole. Initial scout (120 kVp; 10 mA) and transmission (140 kVp; 10 mA) CT scans were obtained for orientation and attenuation correction. Beginning with the intravenous bolus administration of 1,850 MBq (∼50 mCi) of 82Rb (Bracco Diagnostics) in 14 ± 6 (mean ± SD) mL of saline, serial images were acquired for ∼6 min (fourteen 5-s images, six 10-s images, three 20-s images, three 30-s images, and one 90-s image). Immediately after completion of the rest study, a standard intravenous dipyridamole infusion (0.142 mg/kg/min) was administered for 4 min. Three minutes after termination of the dipyridamole infusion, a second dose of 1,850 MBq (∼50 mCi) of 82Rb was injected, and dynamic PET images were acquired in the same fashion. A second CT transmission scan (140 kVp, 10 mA) was then acquired for attenuation correction of the stress images. The heart rate, systemic blood pressure, and 12-lead electrocardiogram were recorded at baseline and throughout the infusion of dipyridamole. The rate × pressure product (RPP) was calculated as the heart rate multiplied by the systolic blood pressure.
The attenuation map used for correction of the 511-keV photon attenuation was derived from the CT scan by use of a continuous conversion scale with a range of slopes dependent on the CT kilovoltage and number of scans (15). Randoms correction was performed by direct subtraction of delayed events, and scatter correction was performed with the scatter correction approach proposed by Bergstrom et al. (16). All dynamic sinograms were reconstructed with attenuation-weighted ordered-subset expectation maximization (21 subsets and 2 iterations, as recommended by the manufacturer of the scanner) into 26 dynamic frames, each with a volume of 128 × 128 × 47 voxels. No postfiltering was performed.
13N-Ammonia PET
All 13N-ammonia studies were performed in the 2-dimensional mode with a whole-body PET scanner (PC-2048 Scanditronix; GE Healthcare). A 10-min transmission scan was first acquired for the correction of photon attenuation. Beginning with the intravenous bolus administration of 13N-ammonia at 925 MBq (25 mCi), serial images were acquired over 19 min (thirty 6-s images and then eight 120-s images). Thirty minutes later, a second transmission scan was obtained to ensure correct positioning of the patient and attenuation correction during stress. Next, intravenous dipyridamole (0.142 mg/kg/min) was infused for 4 min. Three minutes after completion of the dipyridamole infusion, a second dose of 925 MBq (25 mCi) of 13N-ammonia was injected, and images were recorded with the same acquisition sequence. The heart rate, systemic blood pressure, and 12-lead electrocardiogram were recorded at baseline and throughout the infusion of dipyridamole. The RPP was calculated as the heart rate multiplied by the systolic blood pressure.
The attenuation map used for correction of the 511-keV photon attenuation was measured at 511 keV with a 68Ge source. Randoms correction was performed by subtraction of delayed events, and scatter correction was performed with the scatter correction approach proposed by Bergstrom et al. (16). All dynamic sinograms were reconstructed with a filtered backprojection clinical protocol (recommended by the manufacturer of the scanner) into 38 dynamic frames, each with a volume of 128 × 128 × 47 voxels. No postfiltering was performed.
Quantification of MBF
All reconstructed dynamic PET data were analyzed with quantitative dynamic analysis software, which we previously developed and reported (14,17). The software uses generalized factor analysis of dynamic sequences (GFADS), an approach that addresses the nonuniqueness problem in cardiac PET (14,18) by penalizing spatial overlap between factor images, to sample the right ventricular (RV) and left ventricular (LV) blood pools and the LV myocardium to derive the blood pool and tissue time–activity curves for both the 82Rb and the 13N-ammonia studies as described previously (14).
In brief, GFADS was performed and then overlap between factor images was eliminated by modifying the factors and factor images obtained in the first step to minimize the nonnegative term that penalizes the overlap between images of factor coefficients while keeping the matrix product of factor and factor images constant. Therefore, the time–activity curve in each voxel was modeled as a combination of 3 contributions: the contribution from myocardial tissue, modeled with compartment analysis, and contributions from RV and LV blood pools, modeled as fractions of measured LV and RV input functions. Figure 1 shows typical factors and corresponding factor images associated with 82Rb and 13N-ammonia dynamic studies in the same subject. Note that the LV and RV input functions are obtained automatically as the LV and RV factors estimated for the whole factor image, as opposed to a region of interest.
Typical factors and corresponding factor images associated with 82Rb (A) and 13N-ammonia (B) dynamic studies in same subject. AU = arbitrary units; MYO = whole myocardium.
Next, kinetic analysis was performed as described later. The user input consisted of choosing the parameters of the kinetic model (such as type of study [13N ammonia or 82Rb] and number of compartments). The result was a parametric 17-segment polar map (19). The 3 main coronary arteries (left anterior descending artery [LAD], left circumflex coronary artery [LCX], and right coronary artery [RCA]) were overlaid on the polar map to allow direct reading of the mean flow in each coronary territory.
Tracer Kinetic Model
MBF for 82Rb was obtained by fitting the 82Rb time–activity curves to a 2-compartment kinetic model as described previously (20). The 2 compartments of the model are the “free rubidium space” (blood perfusing the myocardium and the interstitial space) and the “trapped rubidium space” (myocardium). The main parameters of the model are the kinetic transport constants K1 (mL/min/g) and k2 (min−1), which denote the extraction (forward) and egress (backward) rates of transport between the metabolically trapped space (myocardium) and the freely diffusible space (blood pool), respectively. To estimate MBF from measures of K1, we used the extraction fraction (E) reported previously for an open-chest procedure on dogs by Yoshida et al. (21):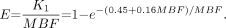
Eq. 1
Equation 1 was solved for MBF by use of the fixed-point iteration approach (22). Because the equation does not have a solution for high MBF values, we used the following linear extrapolation for K1 values of greater than 0.92 mL/g/min to allow for extraction fractions for flow values of greater than 3.7 mL/g/min while ensuring continuity of the function:
Eq. 2
The tissue time–activity curve in each voxel, CT(t), was modeled as a combination of 3 contributions: the contribution from myocardial tissue, modeled with the 2-compartment model, and contributions from LV and RV cavities, modeled as fractions of measured LV and right RV input functions:
Eq. 3where 
is the value at time t for polar map sector i (1 ≤ i ≤ 17); 
is the time–activity curve for sector i; 
is the measured LV input function;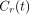 
is the measured RV input function; and 
, 
, 
, and 
are the kinetic parameters for sector i, where 
(mL/min/g) characterizes myocardial tissue extraction (inflow), 
(min−1) characterizes myocardial tissue egress (outflow), 
(dimensionless) represents the contribution to the total activity from the blood input function 
, and 
(dimensionless) represents the contribution from the activity in the RV [
], which differs, in general, from the input function 
.
For 13N-ammonia, MBF was obtained by fitting the 13N-ammonia time–activity curves to a previously validated 3-compartment model (2). The 3 compartments assumed in the model are arterial blood, the interstitial and free cellular space, and the metabolic space. The activity concentration in LV arterial blood is denoted Ca(t), that in RV arterial blood is denoted Cr(t), that in the interstitial and free cellular space is denoted CE(t), and that in the metabolic space is denoted CG(t). We denoted 
as the value of the tissue time–activity curve at time t in polar map sector i (1 ≤ i ≤ 17). The formalism used for 82Rb was also used for 13N-ammonia; that is, 
(mL/g/min), 
(1/min), and 
(1/min) were used as the kinetic parameters for the 13N-ammonia compartment model. The tissue time–activity curve, 
, can be expressed as:
Eq. 4where 
and 
correspond to the fractions of LV input and LR input in the tissue and, therefore, model the vascular fraction in the tissue and the spillover from the left and right ventricles. Differential equations corresponding to the kinetic model were solved with the fourth-order Runge–Kutta approach (23). Nonlinear optimization of the kinetic parameters (
, 
, 
, 
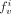, and 
) was performed with the Marquardt least squares method. As validated and reported by Muzik et al. (2), the extraction fraction for the range of blood flow values in the present study was assumed to be one. Thus, blood flow was calculated as the value for 
.
Intra- and Interobserver Reliability
The estimation of MBF was performed by 4 independent observers to assess interobserver variability, and MBF was estimated separately 4 times to assess intraobserver variability. All observers were instructed with a separate teaching dataset on how to follow the same rules in selecting a large volume of interest encompassing the heart to perform factor and compartment analyses and to perform oblique rotations into a short axis and vertical and horizontal long axes to estimate a polar map. The compartment analysis was performed for each sector of the polar map. The mean estimates for the 4 measurements of flow at rest and flow during stress were used to assess the variability introduced by the factor and compartment analyses. Finally, the reproducibility of the 82Rb imaging itself was assessed by comparing MBF measured at rest and MBF measured during peak stress at visits 1 and 2.
Statistical Analyses
The Spearman (ρ) nonparametric correlation coefficient (24) was used to assess the reproducibility of MBF quantitation by 82Rb PET at visits 1 and 2 and for comparison of MBF estimates obtained with 82Rb and 13N-ammonia. Bland–Altman plots of the residuals (difference between mean MBF values in repeated 82Rb studies or in 82Rb and 13N-ammonia studies) against the means were also constructed to assess any systematic error or bias (25,26).
The intraobserver variability in estimating MBF with 82Rb was assessed by averaging all 4 estimates of MBF made by each observer and computing the coefficient of repeatability for the GFADS and the compartment analysis in the rest and stress studies. The interobserver reliability was assessed by computing the average measured intraclass correlation among the 4 observers (and applying the Spearman–Brown correction) by use of a 2-way mixed-effects model with absolute agreement definition and then computing the interrater reliability coefficient. The interobserver variability in estimating MBF with 82Rb was assessed with the Spearman (ρ) nonparametric correlation coefficient (24). A P value of less than 0.05 was used to define statistical significance.
RESULTS
Study Population and Systemic Hemodynamics
Table 1 summarizes the characteristics of the study population for the reproducibility and accuracy portions of the study. The reproducibility cohort consisted of 20 healthy volunteers and 22 subjects (11 men and 11 women; mean age, 48 y) who were at risk for CAD (n = 2), as evidenced by the presence of coronary risk factors (such as prior myocardial infarct or CAD), or who had prior CAD (n = 1). Twenty subjects (12 women and 8 men; mean age, 34 y) participated in the accuracy study and included 19 healthy volunteers and 1 subject at risk for CAD with prior CAD.
Characteristics of Study Cohorts
Table 2 summarizes the systemic hemodynamics of the study cohorts. The resting heart rate, systolic blood pressure, mean arterial blood pressure, and RPP were similar in both PET studies for each study cohort. During dipyridamole stress, the heart rate and the RPP increased similarly, whereas the blood pressure remained unchanged in both study cohorts.
Per-Patient Analysis of Systemic and Coronary Hemodynamics
MBF, CFR, and Coronary Vascular Resistance
Per-Patient Analysis
The baseline MBF was regionally homogeneous and similar in the 2 PET studies performed for each subject in the reproducibility and accuracy cohorts (Table 2). During hyperemia, blood flow increased and coronary vascular resistance decreased homogeneously and significantly (P < 0.05, as determined with paired Student t test) in the 2 PET studies performed for each subject in the reproducibility and accuracy cohorts (Table 2). RPP-normalized rest MBF and peak stress MBF in subjects enrolled in the reproducibility study were not significantly different from those in subjects enrolled in the accuracy study (Table 2). Consequently, estimates of coronary vasodilator reserve in subjects in the reproducibility study were not statistically significantly different from those in subjects in the accuracy study (Table 2).
Per–Vascular Territory Analysis
Tables 3 and 4 show the rest and peak stress mean MBF values in the 3 main coronary territories (LAD, LCX, and RCA) as well as the CFR obtained with repeated 82Rb PET scans in the reproducibility study and with 82Rb and 13N-ammonia in the accuracy study. No statistically significant differences were observed at the level of P < 0.05 in any of the LAD, LCX, or RCA territories in repeated 82Rb studies at rest or during peak stress or when estimating the CFR. Figure 2 shows a typical example of 82Rb and 13N-ammonia stress studies performed in the same subject. Transverse, coronal, and sagittal slices as well as short-axis, vertical-long-axis (VLA), and horizontal-long-axis (HLA) are shown along with polar maps of relative perfusion and absolute MBF in the typical display of our quantitation software. Note the lower spatial resolution in the 82Rb PET study than in the 13N-ammonia PET study, mainly because of the greater positron range of 82Rb (full width at half maximum, 1.6 mm) than of 13N-ammonia (∼0.28 mm).
Transverse, coronal, and sagittal slices (left) as well as short-axis, long-vertical-axis, and horizontal-axis images (top right) of 82Rb (A) and 13N-ammonia (B) stress studies in same subject. Polar maps of relative perfusion (center) and absolute hyperemic MBF (right) are also shown (bottom right); white corresponds to highest values in color scale.
Per–Vascular Territory Analysis of Reproducibility of MBF, CFR, and Coronary Vascular Resistance (CVR)
Per–Vascular Territory Analysis of Accuracy of MBF, CFR, and Coronary Vascular Resistance (CVR)
Intra- and Interobserver Reliability
Figure 3 shows the intraobserver and GFADS variability of the estimation of MBF at rest and MBF during stress, which can be imputed to factor and compartment analyses and, to a lesser extent, to observer variability because the processing was fully automated—except for the choice of the volume of study and the quality control of the polar map generation. Similar results were obtained for the reproducibility of the estimation of CFR. Our results indicated excellent reproducibility of our quantitative dynamic 82Rb approach based on factor and compartment analyses for the estimation of MBF (R2 = 0.99) and CFR (R2 = 0.97). The coefficients of repeatability for the estimation of MBF at rest, MBF during peak stress, and CFR were 1.7%, 1.4%, and 2.8%, respectively.
Intraobserver and GFADS variability of estimation of rest MBF and stress MBF with 82Rb. Mean values for flow from 4 repeated estimates are shown for one observer.
The interobserver variability among the 4 observers who participated in the present study is shown in Figure 4 for the estimation of CFR. Similar results were obtained for the estimation of MBF at rest and MBF during stress. The interobserver variability between any 2 observers for the estimation of MBF and CFR was also very good, with correlation coefficients of greater than 0.87. Similar results were obtained for the estimation of MBF at rest and MBF during stress.
Interobserver variability of estimation of CFR with 82Rb.
Table 5 shows the Spearman ρ nonparametric correlations. All of the correlations were greater than 0.827 and statistically significant at the 0.01 level (2-tailed test). Finally, the intraclass correlation coefficients, reflecting the variability of different MBF measurements in the same subject relative to the total variation across all MBF measurements and all observers, were 0.8271 for rest 82Rb MBF estimates (lower limit, 0.7419; upper limit, 0.8934) and 0.9058 for stress 82Rb MBF estimates (lower limit, 0.8552; upper limit, 0.9432). The corresponding interobserver reliability coefficients were 0.950 at rest and 0.975 during peak stress.
Spearman ρ Nonparametric Correlations Among 82Rb PET Estimates of MBF Obtained by 4 Observers
Reproducibility of 82Rb PET Estimates of MBF
Figure 5 shows the correlations between MBF estimates obtained for the 3 main coronary territories (LAD, LCX, and RCA) at rest and during peak stress in repeated 82Rb studies as well as the corresponding Bland–Altman plots. The reproducibility of MBF estimates (R2 = 0.935) and that of CFR estimates (R2 = 0.841) were very good. Furthermore, the slope of the correlation line was not significantly different from one when estimating MBF (slope, 0.986) or CFR (slope, 0.960) in repeated 82Rb studies. The coefficients of repeatability computed from the Bland–Altman plots were 15.2% for rest MBF and 16.0% for stress MBF and CFR. Furthermore, almost all differences between estimates obtained at visit 1 and those obtained at visit 2 were within the mean ± 1.96 SDs for both rest MBF and stress MBF, and no absolute systematic error was observed.
Reproducibility of rest MBF and stress MBF estimated with 82Rb at 2 visits. (A) Correlation plot of 2 MBF measurements. (B) Bland–Altman plot of 2 MBF measurements.
Accuracy of 82Rb PET Estimates of MBF
Figure 6 shows the correlations between MBF estimates obtained for the 3 main coronary territories at rest and during peak stress in 82Rb and 13N-ammonia studies. Very good correlations were obtained between the 82Rb studies and the 13N-ammonia studies (R2 = 0.857) for MBF ranging from 0.5 to 3 mL/g/min. The Bland–Altman plots revealed no significant proportional error for rest MBF or stress MBF and no dependence of the variations on the amplitude of MBF at rest or during stress. Furthermore, virtually all differences between estimates obtained with 13N-ammonia and those obtained with 82Rb were within the mean ± 1.96 SDs for both rest MBF and stress MBF. Compared with 13N-ammonia, 82Rb resulted in a small systematic overestimation of MBF at rest (0.129 mL/g/min) and an underestimation of MBF during stress (0.22 mL/g/min). The overall error was an underestimation of MBF of 0.04 mL/g/min by 82Rb compared with 13N-ammonia.
Comparison of rest MBF and stress MBF estimated with 82Rb and 13N-ammonia. (A) Correlation plot of 82Rb and 13N-ammonia MBF measurements. (B) Bland–Altman plot of 82Rb and 13N-ammonia MBF measurements. Bland–Altman plot illustrates slight overestimation of MBF at rest and underestimation during peak stress with 82Rb compared with 13N-ammonia.
The correlation between CFR estimates obtained with 13N-ammonia and 82Rb was slightly lower (R2 = 0.633) than that for MBF, with CFR values ranging from 1 to 4.5. This finding was not unexpected because errors in the estimation of MBF at rest or stress will tend to magnify errors in the estimation of CFR (because CFR is calculated as peak MBF during stress/MBF at rest). Furthermore, the Bland–Altman plots for CFR revealed no significant proportional error and no dependence of the variations on the amplitude of CFR for values between 1 and 4.5. Furthermore, all differences between CFR estimates obtained with 13N-ammonia and 82Rb were within the mean ± 1.96 SDs. A systematic underestimation of CFR was observed with 82Rb (0.58), presumably because of the smaller extraction fraction of 82Rb.
These results were consistent with the results of paired Student t tests performed on MBF values obtained with 82Rb and 13N-ammonia. At rest, there was no significant difference at P < 0.05 in the LAD (t = 1.5) and the LCX (t = 1.1), but there was a small significant difference in the RCA (t = 2.6). During stress, there was no significant difference between MBF values obtained with 82Rb and 13N-ammonia in the LCX (t = 2.1) and the RCA (t = 0.5), but there was a marginal significant difference in the LAD (t = 2.3).
DISCUSSION
The detection of coronary artery stenosis and the evaluation of its physiologic significance (i.e., myocardial ischemia) have remained the central paradigms of the diagnosis and management of CAD. Myocardial perfusion imaging represents a robust approach to diagnosing obstructive CAD, quantifying the magnitude of jeopardized myocardium, and assessing the extent of myocardial viability. However, this approach often uncovers only the territory supplied by the most severe coronary artery stenosis and is inadequate to define the presence of multivessel CAD or diffuse microvascular dysfunction; these limitations may explain the paradoxical underestimation of clinical risk by a normal scan pattern in high-risk cohorts (e.g., subjects with diabetes). These limitations are widely recognized and apply to both SPECT and PET. The absolute quantification of MBF has been proposed as a possible solution to the underestimation of jeopardized myocardium by stress myocardial perfusion imaging. Previous studies suggested that the absolute quantification of regional myocardial perfusion (in mL/min/g) with 82Rb is feasible. However, there are very few data on the accuracy and reproducibility of such measurements, which represent the main focus of the present study.
We used the GFADS approach (14) to estimate noninvasively the LV and RV input functions from the dynamic 82Rb and 13N-ammonia PET studies, and we used these estimates in the subsequent kinetic analysis. After fitting of the time-varying factor model to the dynamic data with a least squares objective function, a different objective function that penalized spatial overlap between factor images was minimized. Our approach does not require a priori knowledge of kinetics and can be used in other dynamic imaging applications, such as imaging with 15O-water. Furthermore, our approach does not require drawing of volumes of interest to obtain LV and RV input functions. This feature is a major advantage because it obviates manual intervention in the quantitation scheme and makes the approach reproducible in the clinical setting. Although the number of factors must be defined before GFADS is performed, we found that P = 3 always yielded robust estimates of LV and RV input functions in all patient studies included in this work, as well as in more than 500 patient studies performed in our clinic. This finding is consistent with the fact that the first 3 eigenvectors obtained by principal components analysis were consistently several times higher than the other eigenvectors.
Ideally, GFADS provides independent factor images of the LV, RV, and myocardium. Therefore, kinetic model fitting with the blood time–activity curves derived from GFADS should essentially subtract the influence of LV and RV blood from the myocardial contribution, making a partial-volume correction for spillover unnecessary with our approach. Therefore, spillover attributable to myocardial contamination by the input function or to cardiac motion translates into an overestimation of 
and 
but not of k1 or k2. The fitting of rv for all myocardial territories comes at the cost of a potential increase in the variance of this fit because some territories are not affected by RV spillover. In the compartment model, spillover from tissues was ignored for myocardial curves. Spillover to LV and RV from surrounding tissue is likely to be minimal because geometrically LV and RV are separated from surrounding tissue by the myocardium. Furthermore, we did not model spillover from lung tissue because lung retention of 82Rb was previously reported by Chow et al. (27) to be very low (myocardial-to-lung activity ratio, 12:1). Such high values suggest a very low lung retention compared with myocardial retention and make lung spillover negligible. Spillover from the myocardium into the lung, on the other hand, may result in an underestimation of myocardial tissue concentration, which in turn may affect MBF quantification. Note that lung retention is much greater in 13N-ammonia cardiac PET than in 82Rb cardiac PET, especially in people who smoke and in patients with a low ejection fraction.
Our results show that estimation of MBF with dynamic 82Rb PET is highly reproducible when generalized factor analysis is used to semiautomatically estimate LV and RV input functions and regional compartment analysis while modeling the extraction fraction for 82Rb as a function of flow over a wide range of MBF values (0.7–5 mL/g/min). Our results are consistent with our previous findings (14) showing that reproducibility in realistic Monte Carlo simulations of MBF estimation with image-based estimation of input functions with GFADS and compartment modeling was substantially and significantly better than that of manual drawing of small regions of interest over the LV and RV regions of the reconstructed volumes followed by compartment modeling. The high reproducibility of MBF quantitation was achieved by requiring minimal intervention from the observer that consisted in delineating the large volume of study that encompasses the heart where all analyses were performed. No statistical differences were observed in any coronary territory in repeated 82Rb studies at rest or during peak stress. This finding is consistent with results previously reported by Nagamachi et al. in the case of 13N-ammonia (28). The excellent interstudy reproducibility with 82Rb is comparable to that reported for 13N-ammonia (∼11%) by Nagamachi et al. (28). We also observed excellent intra- and interobserver reliability of our quantitative approach, which is likely related to the fact that it requires minimal observer intervention.
We have shown that the GFADS approach used in this study to estimate noninvasively the LV and RV input functions from the dynamic 82Rb and 13N-ammonia PET studies is highly reproducible (14). After fitting the time-varying factor model to the dynamic data using a least squares objective function, a different objective function which penalized spatial overlap between factor images was minimized. Our approach does not require a priori knowledge of kinetics and can be used with other radiotracers. Furthermore, our approach does not require drawing of volumes of interest to obtain LV and RV input functions. This feature is a major advantage because it obviates manual intervention in the quantitation algorithm and likely is responsible for the excellent results in the reproducibility analysis presented in this study. Although the number of factors must be defined before performing GFADS, we have found that P = 3 always yielded robust estimates of LV and RV input functions in all patient studies included in this work. This is consistent with the fact that the first 3 eigenvectors obtained by principal components analysis were consistently several times greater than the other eigenvectors.
Our results show that 82Rb flow estimates correlated very well with 13N-ammonia flow estimates for flow values that ranged from 0.5 to 2.5 mL/g/min. We observed a small systematic overestimation of rest MBF (0.129 mL/g/min) and an underestimation of stress MBF (0.22 mL/g/min) with 82Rb. Several authors have measured the 82Rb extraction fraction in animal models (21,29,30), and we have previously reported reasonable agreement among these models over the flow range of interest for healthy subjects and patients with mild CAD (e.g., 1 ≤ flow ≤ 3.5 mL/g/min), as is the case in our present work (31). Nonetheless, the inaccuracies in the estimation of MBF with 82Rb compared with 13N-ammonia, especially during peak stress, may be related to the lower extraction of 82Rb and the difficulties with its modeling as well as the lack of modeling of veinous egress.
In the accuracy study, systolic and mean arterial blood pressures and RPP tended to be lower when the subjects underwent the 13N-ammonia study. These differences are most likely related to the sequence of the 2 scans, which for logistical reasons included the 82Rb study before the 13N-ammonia evaluation in most of the subjects. In addition, the fact that subjects were studied at 2 different hospitals, with potential differences in scanner room temperature and other factors, may have also contributed to the observed differences in resting hemodynamic parameters. Nonetheless, resting MBF was normalized to the RPP to account for within-group (reproducibility and accuracy) differences in resting cardiac work.
Despite our best efforts, we had few patients with documented CAD and none with evidence of stress perfusion defects. Furthermore, our extraction fraction model was not validated in a pathologic situation. Thus, our findings regarding the reproducibility and accuracy of MBF estimates with 82Rb cannot be readily extrapolated to areas of low or very low blood flow (e.g., myocardial infarction). However, these areas of low blood flow are readily identifiable on visual or circumferential profile analyses. Thus, it is unlikely that absolute quantification of MBF would enhance diagnosis or risk assessment based on flow estimates in areas of obvious stress-induced ischemia or infarction.
CONCLUSION
Absolute quantitation of MBF with 82Rb dynamic cardiac PET is reproducible and accurate compared with 13N-ammonia. The reproducibility of the quantitative approach itself, as assessed by the intra- and interobserver reliability and that of repeated 82Rb studies, was very good, with slopes of the correlation lines very close to unity. The correlation between MBF estimates obtained at rest and during peak stress with 82Rb and 13N-ammonia studies was also very good, with no significant proportional error and no dependence of variations on the amplitude of the MBF over the range of MBF values considered in the study.
Acknowledgments
This work was supported in part by grants from the National Institutes of Health (RO1-EB005876) and the American Heart Association (GIA-655909T) and by an unrestricted educational Bracco Diagnostics grant. The contents of this article are the responsibility of the authors and do not represent the views of the National Institutes of Health or the American Heart Association.
Footnotes
-
COPYRIGHT © 2009 by the Society of Nuclear Medicine, Inc.
References
- Received for publication August 13, 2008.
- Accepted for publication March 23, 2009.
Jump to section
Related Articles
Cited By...
- Coronary Microvascular Function Following Severe Preeclampsia
- Intermuscular Adiposity is Associated with Coronary Microvascular Dysfunction Independently of Body Mass Index and Modifies its Effect on Adverse Cardiovascular Outcomes
- Discovery of cardiac imaging biomarkers by training neural network models across diagnostic modalities
- Cardiovascular Imaging Techniques to Assess Microvascular Dysfunction
- Structural and Practical Identifiability of Dual-input Kinetic Modeling in Dynamic PET of Liver Inflammation
- Myocardial Scar But Not Ischemia Is Associated With Defibrillator Shocks and Sudden Cardiac Death in Stable Patients With Reduced Left Ventricular Ejection Fraction
- Coronary Microvascular Dysfunction and Cardiovascular Risk in Obese Patients
- Reduced Myocardial Flow Reserve by Positron Emission Tomography Predicts Cardiovascular Events After Cardiac Transplantation
- Integrated Noninvasive Physiological Assessment of Coronary Circulatory Function and Impact on Cardiovascular Mortality in Patients With Stable Coronary Artery Disease
- Quantitative Assessment of Coronary Microvascular Function: Dynamic Single-Photon Emission Computed Tomography, Positron Emission Tomography, Ultrasound, Computed Tomography, and Magnetic Resonance Imaging
- Ranolazine in Symptomatic Diabetic Patients Without Obstructive Coronary Artery Disease: Impact on Microvascular and Diastolic Function
- Diagnostic Performance of Resting and Hyperemic Invasive Physiological Indices to Define Myocardial Ischemia: Validation With 13N-Ammonia Positron Emission Tomography
- Excess Cardiovascular Risk in Women Relative to Men Referred for Coronary Angiography Is Associated With Severely Impaired Coronary Flow Reserve, Not Obstructive Disease
- Characterization of 3-Dimensional PET Systems for Accurate Quantification of Myocardial Blood Flow
- Prognostic Value of Coronary Flow Reserve in Patients with Dialysis-Dependent ESRD
- Effect of Outflow Tract Contributions to 82Rb-PET Global Myocardial Blood Flow Computations
- Interaction of Impaired Coronary Flow Reserve and Cardiomyocyte Injury on Adverse Cardiovascular Outcomes in Patients Without Overt Coronary Artery Disease
- Global Coronary Flow Reserve Is Associated With Adverse Cardiovascular Events Independently of Luminal Angiographic Severity and Modifies the Effect of Early Revascularization
- Comparison and Prognostic Validation of Multiple Methods of Quantification of Myocardial Blood Flow with 82Rb PET
- Quantification of Myocardial Blood Flow in Absolute Terms Using 82Rb PET Imaging: The RUBY-10 Study
- Effects of Sex on Coronary Microvascular Dysfunction and Cardiac Outcomes
- Preserved Coronary Flow Reserve Effectively Excludes High-Risk Coronary Artery Disease on Angiography
- Multisoftware Reproducibility Study of Stress and Rest Myocardial Blood Flow Assessed with 3D Dynamic PET/CT and a 1-Tissue-Compartment Model of 82Rb Kinetics
- 2012 ACCF/AHA/ACP/AATS/PCNA/SCAI/STS Guideline for the Diagnosis and Management of Patients With Stable Ischemic Heart Disease: A Report of the American College of Cardiology Foundation/American Heart Association Task Force on Practice Guidelines, and the American College of Physicians, American Association for Thoracic Surgery, Preventive Cardiovascular Nurses Association, Society for Cardiovascular Angiography and Interventions, and Society of Thoracic Surgeons
- 2012 ACCF/AHA/ACP/AATS/PCNA/SCAI/STS Guideline for the Diagnosis and Management of Patients With Stable Ischemic Heart Disease: A Report of the American College of Cardiology Foundation/American Heart Association Task Force on Practice Guidelines, and the American College of Physicians, American Association for Thoracic Surgery, Preventive Cardiovascular Nurses Association, Society for Cardiovascular Angiography and Interventions, and Society of Thoracic Surgeons
- Association Between Coronary Vascular Dysfunction and Cardiac Mortality in Patients With and Without Diabetes Mellitus
- Coronary Vascular Dysfunction and Prognosis in Patients With Chronic Kidney Disease
- Comparison of Clinical Tools for Measurements of Regional Stress and Rest Myocardial Blood Flow Assessed with 13N-Ammonia PET/CT
- Stress Myocardial Perfusion Imaging for Assessing Prognosis: An Update
- Improved Cardiac Risk Assessment With Noninvasive Measures of Coronary Flow Reserve
- Clinical Value of Absolute Quantification of Myocardial Perfusion With 15O-Water in Coronary Artery Disease
- Quantitative Relationship Between the Extent and Morphology of Coronary Atherosclerotic Plaque and Downstream Myocardial Perfusion
- Impaired Myocardial Flow Reserve on Rubidium-82 Positron Emission Tomography Imaging Predicts Adverse Outcomes in Patients Assessed for Myocardial Ischemia
- Leaving Relativity Behind: Quantitative Clinical Perfusion Imaging
- Prediction of Short-Term Cardiovascular Events Using Quantification of Global Myocardial Flow Reserve in Patients Referred for Clinical 82Rb PET Perfusion Imaging
- Quantitative PET Measurements of Myocardial Blood Flow in Young, Healthy Volunteers: What Should We Expect?
- Simplified Quantification of Myocardial Flow Reserve with flurpiridaz F 18: Validation with Microspheres in a Pig Model
- Cardiac PET: A Versatile, Quantitative Measurement Tool for Heart Failure Management
- Cardiac Positron Emission Tomography/Computed Tomography Imaging Accurately Detects Anatomically and Functionally Significant Coronary Artery Disease
- Cardiac PET Imaging for the Detection and Monitoring of Coronary Artery Disease and Microvascular Health
- Low-Dose Quantitative Myocardial Blood Flow Imaging Using 15O-Water and PET Without Attenuation Correction