Research ArticleClinical Investigation

Can Internal Carotid Arteries Be Used for Noninvasive Quantification of Brain PET Studies?

Laura Providência, Chris W.J. van der Weijden, Philipp Mohr, Joyce van Sluis, Johannes H. van Snick, Riemer H.J.A. Slart, Rudi A.J.O. Dierckx, Adriaan A. Lammertsma and Charalampos Tsoumpas
Journal of Nuclear Medicine April 2024, 65 (4) 600-606; DOI: https://doi.org/10.2967/jnumed.123.266675

Abstract

Because of the limited axial field of view of conventional PET scanners, the internal carotid arteries are commonly used to obtain an image-derived input function (IDIF) in quantitative brain PET. However, time–activity curves extracted from the internal carotids are prone to partial-volume effects due to the limited PET resolution. This study aimed to assess the use of the internal carotids for quantifying brain glucose metabolism before and after partial-volume correction. Methods: Dynamic [18F]FDG images were acquired on a 106-cm-long PET scanner, and quantification was performed with a 2-tissue-compartment model and Patlak analysis using an IDIF extracted from the internal carotids. An IDIF extracted from the ascending aorta was used as ground truth. Results: The internal carotid IDIF underestimated the area under the curve by 37% compared with the ascending aorta IDIF, leading to Ki values approximately 17% higher. After partial-volume correction, the mean relative Ki differences calculated with the ascending aorta and internal carotid IDIFs dropped to 7.5% and 0.05%, when using a 2-tissue-compartment model and Patlak analysis, respectively. However, microparameters (K1, k2, k3) derived from the corrected internal carotid curve differed significantly from those obtained using the ascending aorta. Conclusion: These results suggest that partial-volume–corrected internal carotids may be used to estimate Ki but not kinetic microparameters. Further validation in a larger patient cohort with more variable kinetics is needed for more definitive conclusions.

Fully quantitative PET studies of the brain provide a more accurate assessment of the underlying physiologic processes than SUV analyses. In contrast to SUV analysis, kinetic modeling corrects for confounding factors that contribute to the PET signal, such as variations in tissue perfusion, transport rate, and tracer clearance over time (1).

In general, kinetic modeling requires an arterial input function, describing the concentration of parent tracer in arterial plasma over time. The gold-standard technique for obtaining this function is through continuous arterial sampling after arterial catheterization. This is, however, an invasive and laborious procedure, making it less practical for clinical routine (2), and it may discourage some subjects from participating in research studies because of the discomfort of placing an arterial line (3). To avoid arterial cannulation, image-derived input functions (IDIFs) have emerged (4,5) as an alternative noninvasive approach to obtain the arterial input function.

Extracting an IDIF from large blood pools such as the left ventricle and the aorta has been widely validated since the 1990s (6), making this method suitable for cardiac PET and quantification of regions within the thorax (2). Such large vessels are, however, not available in or near the brain, as conventional PET systems have a relatively short axial field of view ranging from 15 to 30 cm. The largest arteries found near the brain, and that are still included in the field of view, are the internal carotids, with a diameter of 3.9–6.0 mm (7), making them the best candidate for IDIF extraction in quantitative brain studies (8–10). However, the internal carotids’ size is comparable to the spatial resolution of PET, and therefore extraction of tracer concentrations from these vessels is prone to partial-volume effects (2,3). Even though the use of the internal carotids has been validated in several studies (8,11,12), laborious and complex procedures are needed to correct the raw time–activity curves for partial-volume effects. In addition, these methods for partial-volume correction (PVC) often are tailor-made for a specific cohort of patients or radiotracers and cannot be easily extended for general use. Examples of PVC methods include count recovery models (11), blood-based techniques (8), and methods based on segmentation of the carotids using coregistered MR images or MR angiography (12). A purely PET-based noninvasive PVC method that does not require additional medical images or blood sampling is necessary for the wider translation of kinetic analysis using IDIFs in both research and clinical practice.

Iterative deconvolution methods (IDMs) have emerged as a PVC technique that relies solely on PET images and can be used to increase image resolution (13,14). Until now, IDMs have been investigated for correcting partial-volume effects only in brain tissue, and not in the carotid arteries. Their performance regarding PVC in the internal carotids is, therefore, still unknown.

The introduction of systems with a long axial field of view provides a solution to the problem of noninvasive brain quantification, allowing for simultaneous imaging of brain and thoracic regions. The IDIF can be derived from a large vascular structure, such as the ascending aorta, which is large enough (25–38 mm) to minimize partial-volume effects. The purpose of this study was to assess the use of the internal carotids for quantification of the metabolic rate of glucose, before and after applying PET-based PVC, using the ascending aorta as the gold standard.

MATERIALS AND METHODS

Patient Population

Eight oncology patients (4 men, 4 women; age range, 61–81 y; mean ± SD, 75 ± 4 y) with suspected lung malignancy, referred for clinical diagnosis, were included in this study. The local Medical Ethics Review Committee of the University Medical Center Groningen waived the need for formal ethical review (waiver METc2020/554).

Data Acquisition

After a delay of 10 s after automated [18F]FDG bolus injection and a saline flush of 30 mL, list-mode PET data were acquired on a long-axial-field-of-view Siemens Biograph Vision Quadra (axial field of view of 106 cm) for 65 min. Patients received a standard weight-based injection of 3 MBq/kg (±10). Data were binned over 42 frames (4 × 10, 16 × 5, 6 × 30, 5 × 60, and 11 × 300 s), and images were reconstructed using an ordered-subset expectation maximization algorithm (4 iterations, 5 subsets) with time of flight and resolution modeling (point-spread function). Data were corrected for attenuation, random coincidences, scattered radiation, dead time, and decay. Reconstructed images consisted of 645 planes of 440 × 440 voxels (voxel size, 1.65 × 1.65 × 1.645 mm) and image resolution of approximately 3.5 mm in the center of the field of view (15). No filter was applied. Image reconstructions were performed using e7tools, a prototype research software package from Siemens Healthineers.

Motion Correction and Interframe Alignment

Dynamic images were originally reconstructed without attenuation correction. Subsequently, the attenuation correction CT was registered to each non–attenuation-corrected PET frame to correct for potential CT-to-PET mismatches, therefore creating a motion-corrected CT frame for each PET frame. This was done using a deep learning–based tool (16) and the open-source software NiftyReg (17) (further details in the supplemental materials, available at http://jnm.snmjournals.org). The motion-corrected CT images were used for reconstruction of the final PET images. Postreconstruction interframe alignment was performed on the slices comprising the head region (∼24 cm) using a cubic spline interpolation. The correction was applied when motion was larger than 3 mm.

PVC

PVC was performed with the reblurred Van Cittert iterative deconvolution technique (18) (details regarding the choice of this method in the supplemental materials). The reblurred Van Cittert technique was used as implemented in the open-source toolbox PETPVC (14). A point-spread function of 4.4 × 4.4 × 3.8 mm (transverse × axial) was chosen on the basis of system acceptance measurements. To identify the most suitable number of PVC iterations for the present data, reblurred Van Cittert technique was used with 4, 8, 12, and 16 iterations. The number of iterations for which the internal carotid time–activity curve had the best correspondence with the ascending aorta time–activity curve was considered as the most suitable for performing IDM. IDM with the selected parameters was applied to the complete dataset, and the resultant images were used to extract corrected internal carotid time–activity curves.

IDIF

The volumes of interest for extracting the internal carotid time–activity curve were obtained by choosing the 4 highest-intensity pixels over 16 consecutive planes for both left and right internal carotids (9). Volumes of interest were defined on an image corresponding to the average of earlier frames (∼60–110 s). Subsequently, these volumes of interest were applied to all frames to generate an IDIF from the internal carotids (IDIFIC). As ground truth, an IDIF from the ascending aorta (IDIFAA) was obtained by placing a 15-mm diameter (∼9 planes) sphere in the center of this structure. The ascending aorta has previously been validated as an alternative to arterial blood sampling showing excellent agreement with the blood time–activity curve (19) and the resulting quantitative parameters (6).

Kinetic Modeling

Volumes of interest in the brain were extracted using the Hammers maximum-probability atlas within PMOD’s PET-only workflow (version 4.105; PMOD Technologies LLC). Regional time–activity curves were generated for whole brain, gray matter (union of parietal lobe, frontal lobe, temporal lobe, and occipital cortex), and white matter (corpus callosum). For each segmented region, quantification was performed using an irreversible 2-tissue-compartment model (2T3k_VB) with 3 rate constants, K1 (mL·cm−3·min−1), k2 (min−1), and k3 (min−1), and a blood volume parameter, VB. In addition, Patlak graphical analysis was performed, assuming that steady-state conditions apply after 30 min (t* = 30 min). Net tracer influx, Ki (mL·cm−3·min−1), was calculated using both the compartment model and Patlak analysis. Additionally, the Patlak intercept was calculated.

Statistical Analysis

Internal carotids and ascending aorta time–activity curves were compared by calculating the areas under the curve (AUC). Differences in model parameters obtained with IDIFIC and IDIFAA were assessed using the paired Student t test or a Wilcoxon signed-rank test, depending on the result of the Shapiro–Wilk test for normality. Agreement between Ki derived with IDIFIC and IDIFAA was analyzed using a Bland–Altman plot. In addition, the correlation of these Ki values was evaluated using Pearson correlation analysis, and values of slope, intercept, intraclass correlation coefficient, and coefficient of determination (R2) were reported. P values lower than 0.05 were considered as statistically significant.

RESULTS

No PVC

Figure 1 shows time–activity curves extracted from the internal carotids and ascending aorta for all 8 patients (SUVmean ± SD per time point). In all patients, the internal carotids significantly underestimated the activity compared with the ascending aorta. The mean AUCs of the full curves, peaks, and tails are shown in Table 1. Overall, the AUC of the internal carotids showed an underestimation of 37%, 47%, and 34% for full curve, peak, and tail, respectively, compared with the ascending aorta.

FIGURE 1.
FIGURE 1.

Time–activity curves (mean of 8 patients) derived from ascending aorta (AA) and internal carotids (IC): complete curve with time in logarithmic scale (A) and AUC (B). Shadows represent SD for each time point across studied population.

View this table:
TABLE 1.

Mean AUCs of Ascending Aorta and Internal Carotid Curves for [18F]FDG

Mean kinetic parameters for white matter, gray matter, and whole brain obtained using IDIFIC and IDIFAA are shown in Table 2. In the case of the 2T3k_VB model and for all 3 brain regions, K1, k3, and Ki derived using IDIFIC were significantly different from those obtained using IDIFAA, with K1 and Ki being systematically overestimated by the internal carotids and k3 underestimated. No significant difference was observed for k2. For the Patlak analysis of all 3 brain regions, both Ki and intercept derived using IDIFIC were significantly different (overestimated) from those obtained using IDIFAA.

View this table:
TABLE 2.

Mean Model Parameters Obtained with 2T3k_VB and Patlak Analysis Using [18F]FDG, Derived with IDIFAA and IDIFIC

PVC: Parameter Optimization

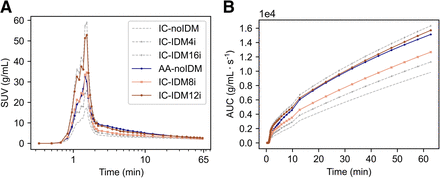
Figure 2 shows the time–activity curves extracted from the internal carotids (mean ± SD per time point) after applying IDM with 4 (IDM4i), 8 (IDM8i), 12 (IDM12i), and 16 (IDM16i) iterations to the original images. Both internal carotids and ascending aorta time–activity curves extracted from the original images (i.e., no IDM) are also shown for comparison. The internal carotid time–activity curves before and after IDM (referred to as IC and IC-IDM, respectively), were compared with the original ascending aorta time–activity curves, for which no IDM was applied: as demonstrated in Figure 3, larger structures such as the ascending aorta are not affected by partial-volume effects. The internal carotid time–activity curve after IDM4i underestimated the activity compared with the ascending aorta time–activity curve, both for the peak and for the tail. After IDM8i, the peak of the internal carotids showed good recovery, but the tail was still underestimated. In contrast, after IDM12i and IDM16i, the internal carotid time–activity curves overestimated the peak, but the tail came closer to those of the ascending aorta time–activity curves. On the basis of these results, it was concluded that 4 iterations were not enough to correct the internal carotid time–activity curves. The reconstruction with 16 iterations was also discarded as it provided very similar results to the one with 12 iterations but with the disadvantage of adding more noise due to the additional iterations. The internal carotid curves corrected using IDM8i (IDIFIC-IDM8i) and IDM12i (IDIFIC-IDM12i) were therefore selected for further kinetic analysis.

FIGURE 2.
FIGURE 2.

Time–activity curves (mean of 8 patients) derived from ascending aorta (AA-noIDM) and internal carotids before (IC-noIDM) and after application of IDM with 4 (IC-IDM4i), 8 (IC-IDM8i), 12 (IC-IDM12i), and 16 (IC-IDM16i) iterations: complete curve with time in logarithmic scale (A) and AUC (B).

FIGURE 3.
FIGURE 3.

Time–activity curves (mean of 8 patients) of ascending aorta time–activity curves before IDM and after application of IDM with 8 (AA-IDM8i) and 12 (AA-IDM12i) iterations.

PVC

After parameter optimization, IDM8i and IDM12i were applied to the original images of all patients. The mean AUCs of the full curve, peak, and tail of IDIFIC-IDM8i and IDIFIC-IDM12i are shown in Table 1. After IDM8i, the internal carotid AUC was overestimated by 0.8% in the peak and underestimated by 18% in the tail. With IDM12i, the internal carotid AUC was overestimated by 52% in the peak and underestimated by 1% in the tail.

Kinetic parameters derived using IDIFIC-IDM8i and IDIFIC-IDM12i were compared with those obtained using IDIFAA (Table 3). When using IDIFIC-IDM8i, k2 and k3 were significantly different from those obtained using IDIFAA for all brain regions, but no significant differences were observed for either K1 or Ki. Even though the Ki values estimated with IDIFIC-IDM8i were very close to the ones estimated with IDIFAA (ratio ∼1), this is because both the numerator and the denominator of Ki estimated with the IDIFIC-IDM8i were underestimated by a similar factor, and the errors cancelled out (Supplemental Fig. 1). With the Patlak analysis, and for all brain regions, Ki obtained using IDIFIC-IDM8i was also not significantly different from the one obtained using IDIFAA, but a significant difference was found for the intercept. When IDIFIC-IDM12i was used as input function (Table 3), significant differences were found for all parameters of both the 2T3k_VB model and the Patlak analysis in all 3 brain regions, compared with using IDIFAA.

View this table:
TABLE 3.

Mean Model Parameters Obtained with 2T3k_VB and Patlak Analysis Using [18F]FDG, Derived with IDIFAA, IDIFIC-IDM8i, and IDIFIC-IDM12i

Bland–Altman Plots and Correlation Analysis (Before and After PVC)

Bland–Altman relative difference plots and scatterplots were analyzed to assess the agreement and correlation between Ki derived using IDIFIC, IDIFIC-IDM8i, and IDIFIC-IDM12i and Ki obtained using IDIFAA. The plots comparing Ki derived with IDIFIC-IDM12i and IDIFAA are not shown because of the poor results obtained with the IDIFIC-IDM12i (Table 3) and can be seen in the Supplemental Figures 2 and 3.

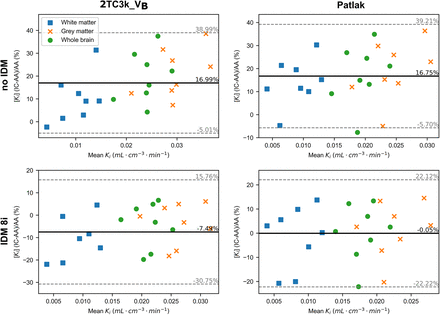
Figure 4 shows Bland–Altman plots for both the 2T3k_VB and Patlak analyses. Without PVC, the Bland–Altman plot revealed a positive bias of 17% in both 2T3k_VB and Patlak analyses. The Bland–Altman plot comparing Ki values derived using IDIFIC-IDM8i with those derived using IDIFAA showed average relative errors of −7.5 and −0.5% for 2T3k_VB and Patlak analyses, respectively.

FIGURE 4.
FIGURE 4.

Bland–Altman relative difference plots of Ki values derived with internal carotids (IC) and ascending aorta (AA) IDIF. First row: Ki derived using IDIFIC vs. IDIFAA (no IDM). Second row: Ki derived using IDIFIC-IDM8i vs. IDIFAA (IDM8i). y-axis represents relative percentage error of internal carotid Ki compared with that of ascending aorta, that is, Embedded Image. Average relative error is represented by solid black line, and upper and lower CI limits are represented by dashed gray lines.

Figure 5 shows Ki correlation plots. Table 4 gives an overview of the values resulting from the correlation analyses, that is, slope, intercept, intraclass correlation coefficient, and R2.

FIGURE 5.
FIGURE 5.

Correlation of Ki values derived using internal carotids (IC) IDIF vs. Ki derived using ascending aorta (AA) IDIF. First row: Ki derived using IDIFIC vs. IDIFAA (no IDM). Second row: Ki derived using IDIFIC-IDM8i vs. IDIFAA (IDM8i). Dashed line corresponds to identity line.

View this table:
TABLE 4.

Results of Correlation Analyses Between Ki Derived Using IDIFAA and Ki Derived Using IDIFIC, IDIFIC-IDM8i, and IDIFIC-IDM12i

DISCUSSION

This study aimed to assess whether the internal carotids can be used to define an IDIF for noninvasive kinetic analysis of [18F]FDG brain PET. Without PVC, internal carotid time–activity curves underestimated blood concentrations compared with those derived from the ascending aorta. Consequently, all kinetic parameters derived using IDIFIC, except for k2, were significantly different from those obtained using IDIFAA. IDIFIC resulted in a significant overestimation of Ki both for 2T3k_VB and for Patlak analysis. To correct for partial-volume effects, a postreconstruction PVC technique, the reblurred Van Cittert method (13,18), was used. The best results with this method were obtained after 8 iterations (IDIFIC-IDM8i), which resulted in a reduction of the error between the internal carotid and ascending aorta AUCs from 47% to −0.8% in the peak and from 34% to 18% in the tail. When IDIFIC-IDM8i was used as the input function in the 2T3k_VB analysis, the estimated Ki values were not significantly different from those obtained with IDIFAA. However, the microparameters K1, k2, and k3 obtained using IDIFic-IDM8i were in general significantly different from those generated using IDIFAA. When IDIFIC-IDM8i was used as the input function in the Patlak analysis, derived Ki values were not significantly different from those obtained using IDIFAA.

The overestimation of Ki when using an IDIFIC without PVC is in agreement with previous studies. For example, Sari et al. (12) showed that when an uncorrected IDIFIC was used, Ki values in white and gray matter were overestimated by 46.2% and 51.0%, respectively, when compared with an input function based on arterial samples. Interestingly, in the present study, Ki overestimation for the uncorrected IDIFIC was only 10.0% and 17.4% in white and gray matter, respectively. The significant improvement in results obtained with an uncorrected IDIFIC may be attributed to several factors. First, the present study was performed using a Biograph Vision Quadra, which has substantially improved sensitivity compared with older scanners. Apart from an overall decrease in noise, the higher sensitivity of the system also allows for reconstructing the first minutes of the scan with shorter frames (2–5 s), resulting in better recovery of the internal carotid peak than when the frames are longer (10 s). Second, we correct for head motion by aligning the original CT images to the individual frames before the final image reconstruction. When head motion is corrected for only by realigning the frames after reconstruction, the attenuation correction is inaccurate and can lead to erroneous activity values possibly affecting the kinetic parameter estimation. Finally, region-of-interest definition may also play a role in the observed differences.

The results of this study show that an uncorrected curve using the internal carotids leads to significantly biased model parameters and to an overestimation of Ki and, therefore, should not be used for quantification. Although this study was performed using [18F]FDG data, the main results should also be valid for other tracers, as partial-volume effects are inherently linked to the size of the object in relation to the PET resolution. After application of PVC, 2T3k_VB Ki values were not significantly different from those obtained using IDIFAA. Similarly, Ki values estimated using Patlak analysis were also not significantly different from those obtained using IDIFAA, and the corresponding Bland–Altman plot showed no bias, indicating that this could be a potential correction method for Ki calculation.

Despite the accurate results obtained for Ki, the microparameters K1, k2, and k3 obtained with 2T3k_VB were still biased, suggesting that the method used in this study, the reblurred Van Cittert, is insufficient to correct for PVC when full kinetic modeling is needed. In line with the present findings, Sari et al. (12) also observed that microparameters K1 and k3 derived using a corrected IDIF still were significantly biased. The reason why biased microparameters lead to accurate Ki estimates remains unclear, but it is known that macroparameters are generally more stable than microparameters, as errors in microparameter estimation might cancel out in the calculation of the macroparameters (Supplemental Fig. 1) (20,21). Nevertheless, compared with previously published values (22), K1, k2, and Ki values estimated using IDIFIC-IDM8i are within the reference range in both white and gray matter; k3, however, is underestimated compared with literature results.

The main limitation of this study is the use of a single point-spread function value to perform deconvolution. Ideally, location-specific measurements of point-spread function for the position of each carotid artery within the field of view should be used when performing IDM. Here, a single value based on system acceptance measurements was used, which may introduce errors when correcting the internal carotids for partial volume. Another limitation is the relatively small sample size used in this study. A larger sample size could potentially yield more robust results.

CONCLUSION

These findings indicate that using an IDIF measured from the internal carotid curve results in overestimation of Ki as well as biased microparameters and should therefore not be used for brain quantification. With the proposed PVC method, Ki values derived using an internal carotid IDIF closely align with those obtained using the ascending aorta as IDIF, suggesting that this PVC method may be of interest for this specific purpose. However, the underlying microparameters still showed significant bias, indicating that a system with a long axial field of view is the best option for noninvasive brain quantification. In the future, to use the internal carotids as input function, a PET system with high spatial resolution is needed.

DISCLOSURE

No potential conflict of interest relevant to this article was reported.

KEY POINTS

QUESTION: Does using the internal carotids for brain quantification result in accurate kinetic parameters?

PERTINENT FINDINGS: In a cohort of 8 patients imaged using a scanner with a long axial field of view, the use of the internal carotids—compared with the ascending aorta—as the input function led to biased kinetic parameters. After PVC, Ki values obtained with the internal carotids were not significantly different from the ones obtained with the ascending aorta, but most of the microparameters were.

IMPLICATIONS FOR PATIENT CARE: The internal carotids should not be used for brain quantification without proper PVC for scanners with at least a 3-mm spatial resolution.

ACKNOWLEDGMENTS

We thank Siemens Healthineers for providing us with the tool for CT-to-PET motion correction and the e7tools, and we thank Dr. Joshua Schaefferkoetter for his guidance.

Footnotes

  • Published online Mar. 14, 2024.

REFERENCES

  1. 1.↵
    1. Huang SC
    . Anatomy of SUV. Nucl Med Biol. 2000;27:643–646.
    OpenUrlCrossRefPubMed
  2. 2.↵
    1. Vanzi E,
    2. Berti V,
    3. Polito C,
    4. et al
    . Cerebral metabolic rate of glucose quantification with the aortic image-derived input function and Patlak method: numerical and patient data evaluation. Nucl Med Commun. 2016;37:849–859.
    OpenUrl
  3. 3.↵
    1. Zanotti-Fregonara P,
    2. Chen K,
    3. Liow JS,
    4. Fujita M,
    5. Innis RB
    . Image-derived input function for brain PET studies: many challenges and few opportunities. J Cereb Blood Flow Metab. 2011;31:1986–1998.
    OpenUrlCrossRefPubMed
  4. 4.↵
    1. van der Weijden CWJ,
    2. Mossel P,
    3. Bartels AL,
    4. et al
    . Non-invasive kinetic modelling approaches for quantitative analysis of brain PET studies. Eur J Nucl Med Mol Imaging. 2023;50:1636–1650.
    OpenUrl
  5. 5.↵
    1. van der Weijden CWJ,
    2. van der Hoorn A,
    3. Wang Y,
    4. et al
    . Investigation of image-derived input functions for non-invasive quantification of myelin density using [11C]MeDAS PET. Neuroimage. 2022;264:119772.
    OpenUrl
  6. 6.↵
    1. Henriksen AC,
    2. Lonsdale MN,
    3. Fuglø D,
    4. Kondziella D,
    5. Nersesjan V,
    6. Marner L
    . Non-invasive quantification of cerebral glucose metabolism using Gjedde-Patlak plot and image-derived input function from the aorta. Neuroimage. 2022;253:119079.
    OpenUrl
  7. 7.↵
    1. Krejza J,
    2. Arkuszewski M,
    3. Kasner SE,
    4. et al
    . Carotid artery diameter in men and women and the relation to body and neck size. Stroke. 2006;37:1103–1105.
    OpenUrlAbstract/FREE Full Text
  8. 8.↵
    1. Chen K,
    2. Bandy D,
    3. Reiman E,
    4. et al
    . Noninvasive quantification of the cerebral metabolic rate for glucose using positron emission tomography,18F-fluoro-2-deoxyglucose, the Patlak method, and an image-derived input function. J Cereb Blood Flow Metab. 1998;18:716–723.
    OpenUrlCrossRefPubMed
  9. 9.↵
    1. Mourik JEM,
    2. Lubberink M,
    3. Klumpers UMH,
    4. Comans EF,
    5. Lammertsma AA,
    6. Boellaard R
    . Partial volume corrected image derived input functions for dynamic PET brain studies: methodology and validation for [11C]flumazenil. Neuroimage. 2008;39:1041–1050.
    OpenUrlCrossRefPubMed
  10. 10.↵
    1. Zanotti-Fregonara P,
    2. Fadaili EM,
    3. Maroy R,
    4. et al
    . Comparison of eight methods for the estimation of the image-derived input function in dynamic [18 F]-FDG PET human brain studies. J Cereb Blood Flow Metab. 2009;29:1825–1835.
    OpenUrlCrossRefPubMed
  11. 11.↵
    1. Srinivas SM,
    2. Dhurairaj T,
    3. Basu S,
    4. Bural G,
    5. Surti S,
    6. Alavi A
    . A recovery coefficient method for partial volume correction of PET images. Ann Nucl Med. 2009;23:341–348.
    OpenUrlCrossRefPubMed
  12. 12.↵
    1. Sari H,
    2. Erlandsson K,
    3. Law I,
    4. et al
    . Estimation of an image derived input function with MR-defined carotid arteries in FDG-PET human studies using a novel partial volume correction method. J Cereb Blood Flow Metab. 2017;37:1398–1409.
    OpenUrlCrossRef
  13. 13.↵
    1. Tohka J,
    2. Reilhac A
    . Deconvolution-based partial volume correction in raclopride-PET and Monte Carlo comparison to MR-based method. Neuroimage. 2008;39:1570–1584.
    OpenUrlCrossRefPubMed
  14. 14.↵
    1. Thomas BA,
    2. Cuplov V,
    3. Bousse A,
    4. et al
    . PETPVC: a toolbox for performing partial volume correction techniques in positron emission tomography. Phys Med Biol. 2016;61:7975–7993.
    OpenUrlCrossRef
  15. 15.↵
    1. Prenosil GA,
    2. Sari H,
    3. Fürstner M,
    4. et al
    . Performance characteristics of the Biograph Vision Quadra PET/CT system with long axial field of view using the NEMA NU 2-2018 standard. J Nucl Med.
  16. 16.↵
    1. Schaefferkoetter J,
    2. Shah V,
    3. Hayden C,
    4. Prior JO,
    5. Zuehlsdorff S
    . Deep learning for improving PET/CT attenuation correction by elastic registration of anatomical data. Eur J Nucl Med Mol Imaging. 2023;50:2292–2304.
    OpenUrl
  17. 17.↵
    1. Modat M,
    2. Cash DM,
    3. Daga P,
    4. Winston GP,
    5. Duncan JS,
    6. Ourselin S
    . Global image registration using a symmetric block-matching approach. J Med Imaging (Bellingham). 2014;1:024003.
    OpenUrl
  18. 18.↵
    1. Carasso AS
    . Linear and nonlinear image deblurring: a documented study. SIAM J Numer Anal. 1999;36:1659–1689.
    OpenUrlCrossRef
  19. 19.↵
    1. van der Weerdt AP,
    2. Klein LJ,
    3. Boellaard R,
    4. Visser CA,
    5. Visser FC,
    6. Lammertsma AA
    . Image-derived input functions for determination of MRGlu in cardiac 18F-FDG PET scans. J Nucl Med. 2001;42:1622–1629.
    OpenUrlAbstract/FREE Full Text
  20. 20.↵
    1. Aston JAD,
    2. Cunningham VJ,
    3. Asselin MC,
    4. Hammers A,
    5. Evans AC,
    6. Gunn RN
    . Positron emission tomography partial volume correction: estimation and algorithms. J Cereb Blood Flow Metab. 2002;22:1019–1034.
    OpenUrlCrossRefPubMed
  21. 21.↵
    1. Sari H,
    2. Erlandsson K,
    3. Marner L,
    4. et al
    . Non-invasive kinetic modelling of PET tracers with radiometabolites using a constrained simultaneous estimation method: evaluation with 11C-SB201745. EJNMMI Res. 2018;8:58.
    OpenUrl
  22. 22.↵
    1. Phelps ME,
    2. Huang SC,
    3. Hoffman EJ,
    4. Selin C,
    5. Sokoloff L,
    6. Kuhl DE
    . Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18)2-fluoro-2-deoxy-D-glucose: validation of method. Ann Neurol. 1979;6:371–388.
    OpenUrlCrossRefPubMed
  • Received for publication September 19, 2023.
  • Revision received January 23, 2024.
Back to top

In this issue

Print
Download PDF
Article Alerts
Email Article
Citation Tools
Bookmark this article

Jump to section

Keywords