MIRD Pamphlet No. 20: The Effect of Model Assumptions on Kidney Dosimetry and Response—Implications for Radionuclide Therapy

THEORETIC BASIS AND MODEL EQUATIONS

The LQ model, with its possible advantages as outlined by Fowler and Stern in 1960 (43), is now used extensively in clinical radiobiology (44). The model is based on the consideration of 2 types of cell killing: single-hit or double-hit DNA events. A single-hit cell kill (type A event) corresponds to a lethal single-ionization event and is thus independent of dose rate. A double-hit cell kill (type B event) can be induced only by 2 closely spaced separate ionization interactions occurring in a short interval and is thus a function of dose rate. The LQ equation for the surviving fraction (SF) of cells after an instantaneously delivered absorbed dose D is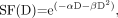Eq. 1where αD is attributed to cell kill from type A events, and βD² from type B events. If the absorbed dose D is delivered over a time T (protracted irradiation), type B events must be corrected for repair of sublethal damage: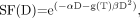Eq. 2where g(T) is a dimensionless function expressing the decrease in lethality from type B events with increasing treatment time, T (44,45). When the duration, T, of the protracted absorbed dose, D, becomes significantly long compared with the repair half-time, then for an absorbed dose delivered at a constant dose rate, g(T) can be approximated by the expressionEq. 3Awhere μ is the rate of repair of sublethal damage (μ = ln 2/T_rep, where T_rep represents the repair half-time constant) (45–51). Equation 3A is derived from the double integration of a constant dose rate (D/T) according to the Lea–Catcheside formulism developed for the incomplete repair model (48,50). For most organs, T_rep ranges between 0.25 and 3.0 h (45), which supports the use of Equation 3A for most radionuclide therapy agents, the notable exceptions being the α-emitters ²¹³Bi, ²¹²Bi, and ²¹¹At and others (42,52,53). A comprehensive characterization of the histopathology of radiation-induced renal failure, renal tubulointerstitial changes after internal irradiation with α-particle–emitting actinium daughters, as well as an examination of agents that can reduce renal toxicity have been reported (53,54). It should be noted that the effects of relative biological effectiveness associated with high–light-energy-transfer radiation are beyond the scope of these analyses and can be incorporated using the method described by Dale (42).

Assuming rapid, near-instantaneous uptake and exponential clearance of activity in a target organ, the time dependence of radiation absorbed dose to the target organ follows an exponential curve with an effective decay constant of λ_e, assuming single-exponential kinetics. In this case, the factor g(T), expressed as a function of the elapsed time T after injection of the radionuclide, is obtained by a double integration method similar to that used in deriving Equation 3A but with an exponential decay term included in the dose-rate function (50):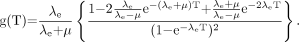Eq. 3BEquation 3B reflects the overall effect of type B damage over the whole of the selected time, T, rather than the instantaneous effect at any particular moment. The term g(T) becomes very small and the quadratic term in Equation 2 diminishes when the effective half-time is much greater than the repair half-time (i.e., λ_e < < μ). With short effective half-lives, g(T) is a more significant factor, especially immediately after injection of the radionuclide and at the onset of radiation absorbed dose delivery to the kidneys.

To account for the biologic effect of dose rate, the LQ model has been used to derive a biologically effective dose (BED). BED is related to the logarithmic cell kill, and because the radiobiologic model parameters differ between tumors and normal tissues, there are different BED values for each irradiated tissue (35,42,43). The original BED is a cell survival model in which all cells receive the same absorbed dose and are subject to the same temporal pattern of absorbed dose. The relative change between tumor BED and critical normal-tissue BED when treatment delivery conditions are altered is therefore a useful indicator in predicting and assessing how the therapeutic index differs in such cases. Therapeutic index is defined in this context as the ratio of probabilities of tumor cure and normal-tissue complications (42). Calculation of tissue-specific BEDs should make it possible to predict the impact of different treatment modalities, including targeted radiotherapy regimes, on the basis of knowledge derived from the effects of external-beam treatments.

The BED is the product of the total absorbed dose (D_T) and a biologic factor designated the relative effectiveness per unit dose, namely:Eq. 4

The main radiobiologic parameters important in conventional radiotherapy are equally relevant for targeted radionuclide therapy. Thus, with temporal variations in dose rate included, the LQ formulation may be applied to this modality also. There are 3 relevant formulae for calculating late-responding normal-tissue BEDs. For fractionated external-beam therapy, the formula is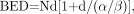Eq. 5where N is the number of fractions and d the dose per fraction and therefore RE = 1 + d/(α/β) and the total absorbed dose D_T = Nd. For continuous therapy at a low, constant dose rate, the formula is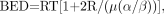Eq. 6where R is the dose rate, T is the elapsed treatment time after administration, and D_T has been expressed as the product RT (32,35,51). For continuous therapy with an exponentially decreasing dose rate, the formula isEq. 7Awhere R₀ is the initial dose rate and λ_e is the effective rate constant describing the loss of radioactivity (assumed to be exponential) from the organ in question. The parameter λ_e is the sum of the radioactive decay rate constant and the organ clearance rate constant (35). In this case, D_T has been expressed as R₀/λ_e. This expression accounts for the radionuclide complete decay where T → ∞. Similarly, the exact expression for times less than infinity is given by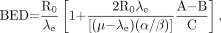Eq. 7B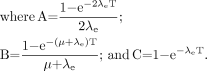

The g(T) factor is implicit in Equation 7B and may be expressed in terms of the g(T) factor described in Equation 3B. Equations 1–3 are relevant for late-responding normal tissues. For tumors and early (acute)-responding normal tissues, either of which may exhibit cellular repopulation during treatment, more complex formulations are necessary (35,49). Also, the temporal pattern of activity uptake and clearance in targeted radiotherapy is complex and may not always be adequately approximated by a monoexponential function, as was assumed in deriving Equation 3A (32,35). Finally, the derivation described by Equations 3B, 7A, and 7B equates radioactivity kinetics with dose-rate kinetics. This equivalence is strictly true only for the self-dose terms. If the target organ is being irradiated by other organ or suborgan components from radionuclides with high photon fluences, then the derivation should account for the impact of cross dose on the target organ dose rate (55).

APPLICATION OF LQ AND BED MODELS TO KIDNEY

If the absorbed dose and dose rate to individual regions of the kidney are known, then it is possible to compute region-specific cell survival taking into account both temporal and spatial distribution of activity. Unfortunately, suborgan, region-specific α- and β-values are not available in the experimental literature and may be derived only by using the α/β-ratios for the whole organ, as these are widely reported (45). Further, BED is conceived of as an average value of homogeneous cell survival and is customarily reported for whole-organ systems to compare toxicities for different irradiation fractionation patterns and tissue radiosensitivities.

In this report, we extend and apply the LQ model to be used with the multiregion kidney model to predict cell survival in different regions of the kidney depending on the model radiosensitivity assumed for these regions and the computed absorbed dose. The factor g(T), introduced in Equation 2, which accounts for incomplete repair as a function of time, can also be used to correct for the low dose rates associated with targeted radiotherapy (43,46). It has been suggested that the kidney be considered a collection of functional subunits (or FSUs) such that it may be useful to view the toxicity in terms of FSU survival rather than survival at a cellular or a whole-organ level. Organ radiotoxicity occurs only if a sufficient number of FSUs are destroyed (29). This approach, which has been gaining theoretic appeal for many organ systems, is based on the assumption that organs consist of independent FSUs. The response of an organ to irradiation depends on individual FSU radiosensitivity and the arrangement of the FSU in the organ architecture. At least 2 distinct arrangements of FSUs have been identified: namely, serial and parallel organ architectures. In the serial organ model, it is assumed that a complication will occur if a single FSU is destroyed by irradiation (e.g., spinal cord, esophagus, or gastrointestinal tract). In the parallel model, it is assumed that there is some threshold value for the fractional number of FSUs that must be eradicated in order for whole-organ complications to manifest. These parallel models have been applied to the complication rate and redundant architecture observed in the kidneys, lungs, and liver (56).

The nephron is the fundamental FSU for the kidney. This FSU is responsible for the formation of urine, and it physically extends from the cortex through the medulla. In the sense that there are 2 kidneys, it can be considered a parallel system, but each kidney in turn is composed of many nephrons (each an FSU) arrayed as parallel elements. In line with the critical volume model described by Niemierko and Goitein (57) and independently described by Källman et al. (58), FSUs may also be identified for different regions of the kidney (e.g., the different cortical segments, or their fractional distribution in the medulla and cortex). In these models that allow for nonuniformity in absorbed dose to an organ, the primary elementary compartment may not conform to a well-defined FSU but rather may be appropriately specified to a volume element or voxel. For example, a region (cluster of voxels) in the cortex may sustain a specific level of damage to nephrons while the kidney still adequately functions. However, if many regions of the cortex are damaged, and the damage is to such an extent that the number of intact FSUs falls below a critical value, the entire organ is likely to fail.

Assuming that this discussion regarding volume-defined FSUs is applicable and, further, that these FSUs have known or parameterized values of α and β, given by (α_Cor, β_Cor) and (α_Med, β_Med) for the cortex and medulla, respectively, the SF of FSUs in the cortex and the medulla can be calculated as follows: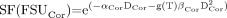Eq. 8

andEq. 9where g(T) is the dimensionless factor correcting for low dose rate, and D_Cor and D_Med are the average absorbed doses in the cortex and medulla, respectively. A combined SF of FSU can also be calculated for the whole kidney, assuming that the number of FSUs in a given region is proportional to its volume:Eq. 10where V_Cor and V_Med are the volumes of the cortex and medulla, respectively. From these last 3 equations, kidney failure can be determined as a function of nonuniform dose and dose rate. The LQ model for high-dose radiation therapy and cellular survival will be used in the examples that follow.

PARAMETERIZATION AND MODEL PREDICTIONS

For a more complete understanding of kidney response to radiation arising from the clearance of therapeutic levels of radiopharmaceuticals in systemic targeted therapy, several potentially relevant examples have been developed. These illustrate the relative importance of dose rate, radiosensitivity, and suborgan spatial nonuniform activity distribution using regionally deposited absorbed dose data and known radiobiologic tissue sensitivity to the formalism presented in Equations 1–10. The cortical region of the kidney is estimated to contain an abundance of the proximal tubule structures and 85% of the glomeruli, which are assumed to be the most radiosensitive target (59–61) for this work. The model calculations assist in understanding the dose–response relationships for existing radiolabeled therapeutic agents used in humans and in predicting the behavior of new agents.

Example 1: Effect of Dose Rate

First, when radiobiologic information is introduced into dose–response relationships, one of the most highly correlated variables is dose rate. Simply, when higher dose rates are delivered to an organ, greater cellular lethality will occur (43,48,51). As shown in the previous section and in Figure 1A, this dose-rate effect is dependent on the intrinsic α/β-ratio (related to tissue radiosensitivity) and the repair half-time for the irradiated tissue.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 1. 

(A) Theoretic illustration of variation of SF of FSU in renal cortex of kidney vs. duration of exposure. Effect of several different half-times of cellular repair on FSU survival is also shown. This illustration assumes that kidney receives uniform average absorbed dose of 15 Gy (D_cor = 15 Gy) and that α_Cor = 0.06 Gy⁻¹ and α_cor/β_Cor = 2.5 Gy based on data idealized from Thames and Hendry (45). As average dose rate is increased by irradiating cortex in shorter time to same total absorbed dose, SF of FSU correspondingly decreases. Longer repair half-times are also associated with decreased capacity for repair after protracted irradiation. (B) SF of FSU in cortex vs. T_eff of radiopharmaceutical (radionuclide conjugate). Model calculation assumes that kidney receives uniform average absorbed dose of 15 Gy (D_cor = 15 Gy) with α_cor/β_Cor = 2.5 Gy. (C) Relative contribution of g(T) for double-hit cell kill due to protracted irradiation, plotted as function of time after injection for radiopharmaceutical with several effective half-lives. Repair half-time for sublethal damage was assumed to be 2 h. Equation 3B was used to derive these curves. (D) Dose volume histograms for absorbed dose distribution by ⁹⁰Y, ¹¹¹In, and ¹⁷⁷Lu in adult male renal cortex (MIRD pamphlet no. 19 model) by homogeneous activity distribution (top) and by inhomogeneous activity distribution (bottom). In both cases, 71% of kidney uptake was in cortex and 29% in medulla. Mean absorbed dose to cortex was 15 Gy according to MIRD pamphlet no. 19 kidney model, with absorbed dose distributions calculated using MCNP Monte Carlo code. Inhomogeneous distribution was modeled to follow uptake structure observed in autoradiographs of kidney segments after ¹¹¹In-DTPA-octreotide administration (66).

Similarly in Figure 1B, to highlight the dose-rate effect in terms of the effective half-time T_eff of the radiopharmaceutical through the kidney, the SF in the cortex is plotted against the T_eff for several values of the tissue repair half-time constant T_rep. A shorter T_eff for the radiopharmaceutical was associated with a higher average dose rate and a corresponding decrease in SF in the cortex.

In Figure 1C, the relative contribution of the quadratic term in Equation 2, which is strongly dependent on dose rate, is shown for different values of T_eff for radiopharmaceutical clearance.

For all effective half-lives, g(T) followed a common curve during the first 10 h. After that time, radiopharmaceuticals with longer T_eff values corresponded to lower values of g(T). For the radiopharmaceuticals with 3- and 6-h effective half-lives, 90% and 69%, respectively, of the total kidney absorbed dose had been deposited by 10 h.

The reference conditions for the classic cases of radiation nephritis are from whole or hemibody external-beam irradiation. Nonuniformity in the radiation absorbed dose to the kidney has been shown to be mostly anatomic (e.g., the urinary collecting ducts and part of the cortices of both kidneys in a 4-field paraaortic lymph node irradiation (62)). In radionuclide therapy, the functional units are irradiated from within. Radioactivity uptake in the kidney is frequently highly nonuniform, as shown by De Jong et al. (63). With nonuniform radioactivity uptake in the kidney cortex comes a corresponding nonuniform dose distribution for high-energy β-emitters, as depicted in Figure 2 of De Jong et al. For an equally nonuniform activity distribution, low-energy β-emitters, such as ¹⁷⁷Lu and other therapeutic agents, will result in less uniformity in the absorbed dose distribution (64,65).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 2. 

SF of FSU vs. absorbed dose ratio between cortex and medulla for renal cortex, renal medulla, whole-kidney multiregion model, and whole-kidney single-region model based on 15 Gy delivered within 6 h (A), 24 h (B), or 72 h (C) from ¹³¹I self-dose contribution to whole kidney. Single-region model can be shown only as single point at cortex-to-medulla absorbed dose ratio of 1.0.

As shown in Figure 1D and by Konijnenberg et al. (66), the absorbed dose nonuniformity in the case of uniform activity distributions of high-energy β-ray emitters such as ⁹⁰Y is mainly in the outer cortex, as calculated using the MCNP Monte Carlo code. Radiation transport of the long-range β-particles to tissues outside the kidney caused a reduction in the absorbed dose to the outer cortex. The absorbed dose volume histogram for the low-energy β-emitter ¹⁷⁷Lu follows closely the human cortex activity distribution, but a build-down region near the outer rim was observed. Animal and human autopsy data have indicated a difference in the size and density of juxtamedullary, midcortically, and outer cortically positioned glomeruli (59–61). The glomeruli were larger in the outer cortex than elsewhere, and the density of glomeruli in the inner cortex was therefore lower near the renal pelvis.

Figures 1A–1C show the dose response of the kidney substructure FSU (cortex) as the dose rate and cellular repair half-time are varied over ranges typically associated with radionuclide therapy and survival-related endpoints. Substantial decreases in survival were a consequence of shorter times for delivering a 15-Gy total absorbed dose when combined with longer half-times for cellular repair. For these examples, we have assumed that if 75% or more of any suborgan target in the kidney loses its function, the function of this component is inactivated. Consequently, because the functional renal cortex and medulla are serial units, the whole kidney will fail if either component ceases to function. Figure 1D shows that the range of particle irradiation contributes to spatial dose nonuniformity.

Example 3: Differential Clearance Rate for Multiregion Kidney Model

The analysis thus far has assumed several effective clearance half-times resulting in corresponding constant low dose rates given in specified intervals to deliver 15 Gy to the whole kidney. In this example, the impact of exponentially decaying low dose rate and a differential clearance between the cortex and medulla is examined. The kinetics for these different kidney compartments are based on renal clearance data obtained in rats, reported by Flynn et al. (67), and dose rate data reported by Green et al. (68). The repair half-time (T_rep) and tissue α/β-values used are the same as in Example 2.

In this example, a relatively short T_eff of 4 h is used to deliver a total average dose of 14.4 Gy in 24 h (96% of 15 Gy delivered over 24 h), providing an initial dose rate of approximately 2.5 Gy/h. A defined interval of irradiation was used in this example in consideration that after substantial decay and clearance of the radioactivity, the dose rate may become sufficiently low and not able to offset the potential for repopulation during prolonged irradiation (32). Figure 3A shows a plot of fractional activity in the whole kidney, medulla, and cortex versus time. A_Cor is defined as the instantaneous activity in the cortex, and A_Med as the instantaneous activity in the medulla. Figure 3A uses differential activity clearance data based on the results of Flynn et al. (67). Those data (67) showed that the ratios of counts in the cortex relative to the medulla for F(ab′)₂, Fab, and a single-chain fragment antibody in rat kidney ranged between 2 and 3 within several hours. The model boundary conditions for Figure 3A have been set to A_Cor/A_Med = 1.0 at t = 0 and A_Cor/A_Med = 3.0 at t = 6 h, assuming single exponential growth of the A_Cor/A_Med ratio over the interval. The activity distribution at t = 0 has been considered to reach transient equilibrium within minutes after injection (69) and is small compared with the T_eff used in the model calculations. After 6 h, the A_Cor/A_Med ratio has been assumed to be constant at 3.0. As expected, the fractional activity remains higher in the cortex than in the medulla at all times except t = 0, and the sum of the cortex and medulla activity is equal to the whole-kidney activity.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 3. 

(A) Fractional activity vs. time after injection for cortex and medulla of kidney (T_eff = 4 h and A_Cor/A_Med = 3.0 at t = 6 h) used as input data for SF calculations shown in B. (B) For irradiation times greater than 6 and 20 h using self-dose contribution from ¹³¹I, cortex SF and whole-kidney SF, respectively, are less than what has been defined as kidney failure line (25% of surviving cells). Irradiated medulla region never falls below minimum SF necessary to sustain function for region.

Equation 3B has been used to reflect the changes in g(T) associated with exponentially decaying dose rate when Equations 8–10 are applied for computing regional FSU survival (Fig. 3B).

Example 4: Differential Uptake and Clearance Rates for Multiregion Kidney Model

Similar to Example 3, the cumulated activity ratio for the cortex and medulla was varied by differential exponential clearance rates by region (cortex and medulla) based on rat clearance data by Flynn et al. (67) with respect to time to show the effect on relative dose to those regions. Parameters for repair half-life, tissue α/β-ratios for the cortex and medulla, were the same as used in Example 2.

In this example, a relatively longer T_eff of 24 h was used to deliver a total average dose of 14.4 Gy over a specified time of 100 h (96% of 15 Gy is delivered in 100 h), with initial dose rates of approximately 0.44 Gy/h. Figure 4A shows the plot of fractional activity in the whole kidney, medulla, and cortex versus time. As with the example shown in Figure 3A, Figure 4A also uses the boundary conditions for differential activity clearance based on the rat clearance data of Flynn et al. (67). These idealized boundary conditions have been set at A_Cor/A_Med = 1.0 at t = 0 and A_Cor/A_Med = 3.0 at t = 6 h, assuming single exponential growth of the A_Cor/A_Med ratio over the interval. After 6 h, the A_Cor/A_Med ratio has been assumed to be constant at 3.0.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 4. 

(A) Fractional activity vs. time after injection for cortex and medulla of kidney (T_eff = 24 h and A_Cor/A_Med = 3.0 at t > 6 h) used as input data for SF calculations shown in B. (B) For all irradiation times using self-dose contribution from ¹³¹I, cortex, medulla, and whole-kidney SF are greater than what has been defined as kidney failure line (25% of surviving cells). No irradiated region ever falls below minimum SF necessary to sustain function for region or kidney as a whole.

Examples 3 and 4 provide a more clinically relevant activity profile as shown in Figures 3A and 4A. These profiles are based on the boundary condition derived from both animal and human measurements (67,70) and provide for the time variation of activity in the cortical and medullary regions to rise from an initial ratio (cortex to medulla) of 1.0 to a ratio of 3.0 in 6 h. In Figures 3B and 4B, increased dose rate resulting from delivering dose by radionuclide therapy in a shorter time (Fig. 3B: T_eff = 4 h) is the primary consideration for increased lethality, as compared with nonuniformity in uptake, for these examples. Furthermore, the potential for increased lethality would be accentuated when activity heterogeneity is introduced in the presumed radiobiologically sensitive target.

CORRELATION OF MODEL PREDICTIONS WITH CLINICAL RESPONSE

Renal failure from nephrotoxicity associated with radionuclide therapy (71) has been recognized as an important clinical event (4–7). This toxicity has been reported as both acute and chronic. Typically, acute effects appear several weeks to months after exposure as a decrease in creatinine clearance. Chronic kidney toxicity may present as an increased level of serum creatinine that does not return toward normal. A mildly elevated serum creatinine level may persist, or renal function may gradually deteriorate and eventually require dialysis. Deaths from toxicity associated with radionuclide therapy have been reported. Biopsies have demonstrated histologic findings of thrombotic microangiopathy similar to the findings of nephropathy in kidneys in the treatment field of external-beam radiation.

Because even the acute effects take several weeks or longer to become apparent, hundreds of patients were exposed to potentially toxic doses of radionuclide therapeutic agents before the toxic effects were appreciated. Many of these patients were enrolled in phase 1 or 2 clinical therapy trials that documented the severity of the toxicity and the corresponding kidney dose estimates. Hence, a significant amount of dose–response data is now available in the radionuclide therapy literature. A brief review of patient data for several of the major clinical trials in terms of accrual (over 700 patients) follows.

Cumulative clinical experience by investigators with ⁹⁰Y-tetraazacyclododecanetetraacetic acid (DOTA)-octreotide in the group from Basel consists of a pilot clinical trial with 29 patients (71), 2 phase 2 clinical studies including 41 patients (72) and 39 patients (73) with neuroendocrine tumors, and a study on 20 patients with medullary thyroid cancer (74). In the initial studies, the investigators reported early renal insufficiency in 4 patients and 2 additional patients in whom coadministration of amino acids for renal protection was not used. These patients received a cumulative activity of more than 7.4 GBq of ⁹⁰Y-DOTA-octreotide per square meter given in up to 4 administrations. In their later studies, which were always performed with amino acids, only a single patient was reported to have grade 2 renal toxicity (74).

A retrospective study of patient-specific kidney dosimetry for 18 patients in a phase I multicenter trial of ⁹⁰Y-DOTA-Tyr³-octreotide was performed by Barone et al. (75). The study was originally designed to give the patients a maximum absorbed dose of 27 Gy to the kidneys. The activity escalation was aimed at a maximum dose per cycle to the target while limiting the total kidney dose to 27 Gy. Some patients were given additional cycles of therapy. Patient-specific kinetics of kidney uptake and clearance were determined by quantitative PET of the positron-emitting analog ⁸⁶Y DOTA-Tyr³-octreotide at 3.5, 24, and 48 h after injection. To reduce uptake of the peptide in the kidneys, an infusion of amino acids was started 0.5 h before injection of the compound and continued for 4 h after injection. The kidney absorbed dose was calculated according to the MIRD schema by using the sex-appropriate phantom in MIRDOSE3 and the kidney residence time for ⁹⁰Y. This study showed no correlation between the MIRD-based kidney absorbed dose and the decrease in serum creatinine clearance, which was monitored regularly. The dosimetry was made more patient-specific by adjusting the computed absorbed dose to the kidney using the CT-derived volumes instead of uncorrected values obtained from phantoms. On average, the specific kidney volumes were larger than the stylized MIRD kidney volume. The volume-corrected kidney dose correlated better with the decrease in creatinine clearance. A stronger correlation was also observed when applying the LQ model–based BED, compared with using absorbed dose alone. By using the BED methodology, one can account for differences in the delivery of dose to the kidney by relatively high or low dose-rate radiation from either external-beam or radionuclide therapy.

A further advantage of using the BED is that the dose–effect relationship for kidney damage after ⁹⁰Y-DOTA-octreotide therapy can be compared with the classic dose–effect relationship for radiation nephropathy after external-beam radiotherapy. A statistically significant approach has been applied by observing the proportion of patients per dose interval in whom nephropathy develops. A decline in creatinine clearance of more than 20% per year over 5 y has been used to indicate end-stage renal disease (75). The dose–response curve for external-beam therapy shows an approximate threshold at 15 Gy, whereas for ⁹⁰Y radionuclide therapy, the threshold has been shifted to 20 Gy (Fig. 5).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 5. 

Dose–response curve for symptomatic radiation nephropathy after external-beam radiotherapy. Curve for normal-tissue complication probabilities based on external-beam radiotherapy data (26) is fitted with TD₅₀ = 28 Gy and at slope of m = 0.15 through external-beam radiotherapy data with statistically significant Pearson score of r = 0.98. External-beam radiotherapy data are based on experience with approximately 300 patients with 120 cases of radiation nephropathy (24); each entry in graph represents at least 10 patients. Absorbed dose per fraction, sample size, and definition of end-stage renal disease varied for external-beam radiotherapy data per Cassady (24) and as indicated in original citations. Clinical data for renal damage after therapy with ⁹⁰Y-DOTA-octreotide from Barone et al. (75) (n = 18) and Bodei et al. (76) (n = 25) were added to generate second (normal-tissue complication probabilities) ⁹⁰Y curve. Minimum decline of 20% per year in creatinine clearance has been used to indicate end-stage renal disease within 5 y (75). This curve was fitted through ⁹⁰Y data with TD₅₀ = 35 Gy and m = 0.18 and Pearson score of r = 0.90. Each ⁹⁰Y data entry represents at least 3 patients, except entry at 19 Gy (Barone et al.), 20 Gy, and 53 Gy (Bodei et al.), which are single patients. Data from Bodei et al. at 53 Gy (arrow) with just 13% rate of creatinine clearance loss per year were considered to be outlier (n = 1). ⁹⁰Y-DOTA-octreotide therapy data were obtained with various dosing schemes compared with external-beam radiotherapy reference conditions of dose uniformity and 2 Gy per fraction (75,77).

Renal toxicity was evaluated in 25 patients by Bodei et al. (76) after peptide receptor radiation therapy (PRRT) with ⁹⁰Y-DOTATOC or ¹⁷⁷Lu-DOTATATE-octreotide. The patients were enrolled in several clinical phase I–II protocols. From 1997 to 2002, 256 patients received treatment with these radiolabeled peptides. Renal toxicity evaluation used creatinine clearance and creatinine toxicity grade as surrogate endpoints. Multiple administrations (2–9 cycles) separated by 1–3 mo were given to a variety of patients with neuroendocrine tumors. BED, instead of absorbed dose, was considered for possible correlation with renal damage, according to Barone et al. (75). BED values for the kidneys were calculated according to the LQ model, with α/β = 2.5 Gy, T_rep = 2.8 h, and T_eff = 42 h.

In Figure 6, Bodei data (76) show that 1 patient of 9 with a BED to the kidneys in the 30- to 40-Gy interval who received 2–4 cycles of PRRT and 5 patients of 8 with a BED in the 40- to 50-Gy interval who received 5 or more cycles had a higher loss in creatinine clearance (>20%/y over 5 y after treatment). Grade I serum creatinine toxicity was observed in 6 patients with a BED to the kidneys over 40 Gy, and grade II creatinine toxicity was observed in 1 patient with a BED greater than 55 Gy. A greater number of cycles with an associated higher total BED appeared to manifest as greater toxicity. Concomitant risk factors seem to be associated with a greater loss of creatinine clearance. One patient with a BED of 67 Gy (RE = 1.25) showed a moderate decrease in creatinine clearance of 13%/y, as shown in Figures 5 and 6 as zero toxicity (statistical outlier) since the threshold of toxicity for these figures was taken to be a creatinine clearance loss of more than 20%/y over 5 y.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 6. 

Dose–response curve for correlation between kidney BED and symptomatic radiation damage to kidneys for external-beam data, compared with ⁹⁰Y-DOTA-octreotide data.

Figure 6 combines the results of both Barone et al. (75) and Bodei et al. (76) into a single set of data (dashed line) in which the fitting of a new line for normal-tissue complication probabilities yields a kidney TD_50/5 (1) of 44 Gy for PRRT BED versus renal damage (m = 0.12, r = 0.99). Each ⁹⁰Y data point represents at least 3 patients within 10-Gy BED intervals, except that the entry at a BED of 28 Gy from Barone has been based on 2 patients. In the data from Bodei, the 22-Gy point has been based on 2 patients, and both the 55-Gy and the 67-Gy points are based on single patients only. The arrow highlights the data from Bodei at 67 Gy, which were not included in the fit and were considered a curve fit outlier as per Figure 5. The BED data associated with external-beam radiotherapy kidney nephropathy (24,26,77) have been replotted for reference (solid line) where the kidney TD₅₀ has also been shown to be 44 Gy. Uncertainties (error bars) associated with the data points presented in Figures 5 and 6 vary widely since these graphs were a compilation of data from nearly a dozen sources over the past 30 y. External-beam radiotherapy data have standard errors in the 5%−10% range where the PRRT data uncertainties ranged from 10% to 25% for entries based on 3 or more patients.

By calculating the BED for each external-beam data point with α/β = 2.5 Gy, the BED data for PRRT radiotherapy (75,78) fit in well with the external-beam radiotherapy–NCTP curve. Because the BED accounts for differences in administration schemes, a steeper dose–effect curve can be fitted through the data. The threshold for kidney radiation damage is approximately a BED of 33 Gy, although none of the 3 patients receiving ⁹⁰Y-DOTA-octreotide therapy (67) with a BED of 41 Gy show high creatinine clearance loss.

Breitz et al. (10,79) reported on the dosimetry and kidney toxicity from skeleton-targeted radiotherapy using a β-emitting radiophosphonate, ¹⁶⁶Ho-1,4,7,10-tetraazacyclododecane-1,4,7,10-tetramethylene-phosphonic acid (DOTMP). Two phase I/II studies were performed to determine the maximum tolerated dose of ¹⁶⁶Ho-DOTMP in combination with high-dose chemotherapy with and without total-body irradiation as a preparative regimen for peripheral blood stem cell transplantation in patients with multiple myeloma (10). Adverse events consistent with radiation toxicity on the genitourinary system (kidney and bladder) presented as a late effect in the phase I studies. Kidney toxicity presented as a permanent increase in serum creatinine (≥grade 2 or greater than 3 times the upper limit of normal) in approximately one third of patients (33/95 patients), and thrombotic microangiopathy was confirmed by biopsy in 5 patients. With 5 y of follow-up, 18 patients treated at the highest doses had received dialysis. This toxicity occurred in the setting of improved response rate and overall survival compared with treatment of similar patients without the addition of ¹⁶⁶Ho-DOTMP (80). The kidney absorbed dose estimates ranged from 0.5 to 7.9 Gy for administered activities of ¹⁶⁶Ho-DOTMP between 12.4 and 126.2 GBq (using the International Commission on Radiation Protection [ICRP] 53 model based on the whole-body clearance method to estimate kidney dose) (10,67). There was a significant relationship of renal toxicity with administered dose and with kidney radiation absorbed dose, although the estimates of kidney absorbed dose were surprisingly low considering the degree of renal toxicity. A third study focused on improving the accuracy of the radiation absorbed dose estimates, particularly to the kidneys, because of unexpected radiation nephropathy (based on absorbed dose estimates) that occurred at the higher administered activities in the phase I studies. Twelve patients were evaluated at lower therapeutic administered activities, receiving 2 tracer administrations of radiopharmaceutical 1 wk apart before therapy to evaluate intrapatient consistency. Clearance of the radioactivity that was not bound to bone surfaces was relatively rapid; 70% of the activity was cleared in the first 12 h (81). Thus, a dose-rate effect could have contributed to the toxicity.

For patients receiving administered activities ranging from 38 to 67 GBq, the estimates of absorbed dose to the kidney varied from 1.6 to 4.0 Gy using the ICRP 53 model (69) and from 8.3 to 17.3 Gy using a scintillation camera imaging method based on quantitation of ¹⁶⁶Ho in the kidneys. The latter method resulted in high interpatient variability that the authors ascribed to technical problems in the imaging process. These problems included accommodating the complex spectrum of ¹⁶⁶Ho, poor camera counting statistics, and high scatter contamination that resulted in high interpatient variability (10,81). BED estimates using the absorbed dose to the kidney reported using the ICRP 53 model (69) (5–7.5 Gy) were somewhat higher (6.5–9.8 Gy) using an RE of 1.3, but substantially less than the corresponding BED threshold for kidney toxicity of 30 Gy calculated by Barone et al. (75). If the dosimetry was derived from the results of the region-of-interest–based scintillation camera method, the initial dose rate, RE, and correspondingly the resultant BED would be substantially increased to the range that Barone reported (75) for clinical kidney toxicity.

The low dose estimates from the ICRP 53 model (69) appeared inconsistent with radiation nephropathy. However, multiple myeloma is a challenging disease on which to draw conclusions on the correlation of kidney absorbed dose and toxicity, because the kidneys are often damaged by the disease and therefore more susceptible to toxicity. Contrast agents are not administered for CT scans in this patient population because of the potentially compromised status of the kidneys. The authors concluded that higher administered activities were associated with the observed kidney toxicity, supporting radiation as the primary cause as confirmed by the histologic findings on kidney biopsy in 5 of the patients. This confirmation led the investigators to use lower administered activities of this radiopharmaceutical in subsequently treated patients.

If one were to extrapolate the RE for data presented by Breitz et al. (10) based on the toxicity observed using an estimated absorbed dose of 7.5–15 Gy to the kidney for those patients receiving over 55.5 GBq/m², the RE would be on the order of 3.0, where REs for low–dose-rate PRRT studies (70–76) are computed in the range of 1.1–1.8 per the example cited in Wessels (82) based on dose-rate considerations alone. A comparison of the relevant observations is illustrated in Table 2.

Table 2 compares the absorbed doses and dose rates to the kidneys with radionuclide therapies based on information available or estimated from published work (10,70–72,75,79–81) and the threshold doses for external-beam radiotherapy, either locally (11) or from total-body irradiation used as a part of the conditioning regimen for bone marrow transplantation (30,77). The range of values for the absorbed doses computed for the kidney and the resultant initial dose rates, the RE and BED values shown in Table 2, for the ¹⁶⁶Ho trials were based on using a range of administered activities up to a maximum of 167 GBq (10) and applying the 2 dosimetry methods reported (79–81).

In a review of the dosimetry and toxicity data associated with PRRT, Cremonesi et al. (83) highlighted the impact that kidney toxicity has played in designing strategies for more effective delivery of tumor doses. Clearing agents, patient-specific CT kidney volumetrics, and maximum dose-rate reduction through multiple-dose administration have played an important role in elimination of kidney toxicity after PRRT. Cremonesi et al. also found that the patients who had a high computed BED after PRRT and an increase of serious kidney toxicity were those who received a relatively few high-dose repeated administrations. These findings were consistent with other reports (71,84,85) suggesting that reductions in initial dose rate from a high number of multiple administrations (cycles) and, whenever possible, prolonged administration of renal protectors for reduction of kidney uptake improves the repair rate for irradiated kidney tissues. Such strategies of increasing the number of fractions and reducing fraction size or dose rate to an equivalent tumor BED are entirely consistent with the successful experience of total-body irradiation for transplant conditioning regimens when lung toxicity was a dose-limiting problem (86,87). In the total-body irradiation example, 9 Gy in 1 treatment was reduced to 1.5 Gy in each of 9 treatments (administered twice per day over 5 d). The BED dose delivered to the bone marrow was the same in both cases, taking advantage of the reduced α/β-ratio of lung compared with that of bone marrow.

DISCUSSION

CONCLUSION

Absorbed dose computed from a uniform distribution of activity in the kidney using standard reference phantoms without regard to the dose rate and spatial nonuniformities will not provide meaningful dose–response correlations.

In clinical trials involving nearly 1,000 patients receiving radionuclide peptide or small-molecule therapy, a significant number of patients experienced renal toxicity. Renal uptake and clearance of large amounts of therapeutic activity was observed in these patients and resulted in their presenting with both acute and late kidney toxicity. This toxicity has decreased in recent years as investigators have altered delivery by using fractionated administrations, have limited the absolute amount of administered activity given in 1 fraction, and have added clearing agents to the treatment regimen.

Improved methods of collecting data can provide the dose estimates needed for radiobiologic model predictions based on absorbed dose to the different kidney regions, taking into account nonuniformity in spatial and temporal dose, dose rate, and repair processes. Calculations using patient-specific measurement of kidney mass in combination with the LQ model and the associated BED concept have improved the correlation between radionuclide therapy toxicity and external-beam experience.

Model applications shown in our examples highlight potential scenarios where toxicity may be predicted and avoided. These include high initial and average dose rates for a short-lived radiopharmaceutical that is observed to localize and be retained in radiosensitive portions of the kidney.

The demonstration that a dose–response curve for radionuclide therapy may correlate with well-established external-beam data suggests that this type of analysis may guide the investigator in determining the safe maximum regional absorbed dose and resulting BED for proposed clinical trials.