Wasserstein Distance-Based Nonlinear Dimensionality Reduction for Depth-of-Interaction Decoding in Monolithic Crystal PET Detector

Introduction: Monolithic crystal PET detectors are studied as an alternative to pixelated crystal detectors and the coordinates of the gamma interaction positions can be estimated from the number of photons detected (light distribution, LD) in each photosensor. Statistics-based positioning (SBP) are widely used to estimate interaction positions in monolithic crystals. SBPs require a calibration set to produce a lookup table (LUT) of LD for interaction position, but Depth-of-Interaction (DOI) calibration at the system level is difficult because it needs side-on irradiation of PET detectors. Therefore, model-based methods and data-driven embedding were attempted for DOI decoding. However, the performance of the model-based method using the sum and maximum of LD can be degraded by the mismatch of model and detector characteristics. Data-driven decoding using Local Linear Embedding (LLE) does not require an exact model but relies on the Euclidean distance in measuring the similarity of LDs. To overcome these problems, we propose the Wasserstein distance-based LLE (W-LLE) for DOI decoding. The Wasserstein distance is a metric defined to compare probability distributions, and a closed-form solution for 1D distribution exists. We validated the feasibility of W-LLE using simulation data and compared it with LLE, t-SNE, and the model-based method.

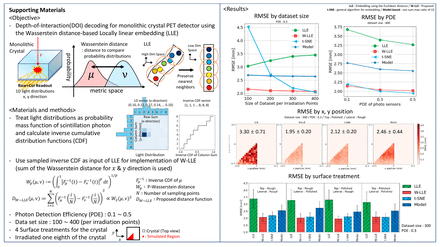
Methods: LLE is an algorithm that finds a low dimensional mapping that preserves neighboring elements computed using Euclidean distance, and the Wasserstein distance between 1D distributions is a function of inverse cumulative distribution function (CDF). To implement the proposed W-LLE, we calculated inverse CDF for LD for x and y-directions, sampled them in vector form, then performed LLE. For LLE and t-SNE, LD vectors for x and y-directions were concatenated and used, and for W-LLE, inverse CDF vectors for x and y-directions were concatenated and used. We used the Scikit-learn 0.24.2, a Python package for machine learning to perform LLE and t-SNE. After embedding, we calculated DOI using the probability distribution of DOI to match the range. The whole data set was obtained via the GATE (ver. 8.2) Monte Carlo Simulation toolkit. We simulated LYSO crystal (25.4×25.4×15 mm³), and an array of photosensors (8×8 arrays of 3×3 mm^2, 3.2 mm pitch). The photon detection efficiency (PDE) of the photosensors was set as 0.1 to 0.5. Row-column readout was used to reduce readout channels. The calibration set was obtained by irradiating the 511 keV point source perpendicularly, and the interval of irradiating points was 1 mm for both x and y-directions. We used the LUT-Davis model for accurate optical modeling. We tested four surface treatment conditions. We randomly sampled the calibration set multiple times and performed DOI decoding because embedding performance is data-dependent. We used the root-mean-square error (RMSE) of DOI to evaluate the algorithms.

Results: W-LLE showed the lowest RMSE (e.g., 2.1 mm RMSE for PDE of 0.3) among tested algorithms except for the case when the data set size is 400. t-SNE showed the lowest RMSE (2.04 mm) when dataset size was 400, but showed significant performance degradation as dataset size decreases. The RMSE of all algorithms increased as the PDE of the photosensor decreased, but the W-LLE showed the smallest change. The model-based method showed a large difference in RMSE according to location, while RMSE of t-SNE and W-LLE does not depend on the location. Surface treatment did not remarkably affect the performance of the algorithms.

Conclusions: By treating LD vectors as one-dimensional probability mass functions and finding neighboring elements using the Wasserstein distance, W-LLE achieved low RMSE in DOI estimation with a small dataset. Although t-SNE showed lower RMSE than W-LLE with enough dataset, obtaining a calibration set with a pencil beam source is time-consuming. Therefore, W-LLE would have a practical advantage in calibration time.

• Download figure
• Open in new tab
• Download powerpoint