Abstract
Preclinical evaluation of new radiopharmaceuticals is performed in animal systems before testing is started in humans. These studies, often performed in murine or other rodent models, are important in understanding the relationship between absorbed dose and response, which can be translated to preclinical results for humans. In performing such calculations, either electrons are assumed to deposit all of their energy locally or idealized models of mouse anatomy are used to determine absorbed fractions. Photon contributions are generally considered negligible. To improve the accuracy of such absorbed dose calculations, mouse-specific S factors for 131I, 153Sm, 32P, 188Re, and 90Y have been generated, and the photon and electron portions have been tabulated separately. Absorbed fractions for 5 monoenergetic electrons, ranging in energy from 0.5 to 2 MeV, are also provided. Methods: Female athymic mouse MR images were obtained on a 4.7-T MRI device. Fifteen T1-weighted, 1.5-mm-thick slices (0.5-mm gap) were collected. Using a previously developed software package, 3-dimensional Internal Dosimetry (3D-ID), organ contours were drawn to obtain a 3-dimensional representation of liver, kidneys, and spleen. Using a point-kernel convolution, the mean absorbed dose to each organ from the individual contributions of each source organ were calculated. S factor equivalent values were obtained by assuming a uniform distribution of radioactivity in each organ. Results were validated by comparing 3D-ID generated electron S factors for different-sized spheres with published data. Depending on matrix size, sphere size, and radionuclide, 1% (2562 matrix) to 18% (642 matrix) agreement was obtained. Results: S factor values were calculated for liver, spleen, and right and left kidneys. Cross-organ electron-absorbed fractions of up to 0.33 were obtained (e.g., 90Y right kidney to liver). Comparisons between S factor values and values obtained assuming complete absorption of electron energy yielded differences of more than 190% (90Y spleen self-dose). Conclusion: The effect of cross-organ and self-absorbed dose is dependent on emission energy and organ geometry and should be considered in murine dose estimates. The approach used to generate these S factors is applicable to other animal systems and also to nonuniform activity distributions that may be obtained by small-animal SPECT or PET imaging or by quantitative autoradiography.
- S factors
- murine model
- dosimetry
- 90Y
- 131I
- 153Sm
- 32P
- 188Re
- monoenergetic electron
Initial assessment of the potential toxicity of investigational radiopharmaceuticals is typically performed using murine or other rodent models. These studies are important in the evaluation of pharmacokinetics and potential toxicity in humans. Generally, numerous animals in each study are injected or implanted with radioactive agents and sacrificed at various times points so that organs and tissues can be examined, weighed, and counted for amounts of activity. Using these data, activity in tissues and organs is often expressed as percent of injected dose.
To understand the effect of the radiopharmaceuticals used in these preclinical studies, it is necessary to examine dose–response relationships in the animal system and to translate the results to the human case. Dose estimates in animal studies are generally obtained using one of several methods. Thermoluminescent dosimeters (TLDs) can be implanted into an animal for in vivo absorbed dose measurements (1). However, TLD measurements are sensitive to the effects of temperature, location of the implant, and pH of the implant environment (2,3). To overcome these problems, new materials are being examined (4).
A second method is to apply MIRD dosimetry methods, which use S factor tables dependent on human organ size and relationships subject to the simplifying assumptions of local energy deposition and negligible cross-organ dose deposition (5–7). However, as previously recognized (8–11), the extension of the MIRD methodology in the human for the determination of absorbed dose to mice in the laboratory is not direct. Issues such as the size and relationship of mouse organs are significantly different from those found in the human anatomy. Furthermore, the difference between human and murine anatomy can be of greater importance depending on the characteristic decay process of the specific radionuclide for which dosimetry is desired. In the case of energetic β-emissions, which have a range that approaches and exceeds mouse organ dimensions, the simplifying assumptions of absorbed fraction (φ) equal to 1 (i.e., source and target organs are the same) no longer holds. In addition, because of the smaller interorgan distances relative to human anatomy, it is necessary to consider cross-organ dose to accurately access the mean absorbed dose to an individual organ.
These limitations have been addressed by previous researchers (8–11), and several steps have been taken to improve dosimetric estimates in the murine model for a variety of radionuclides. In Hui et al. (8), a geometric mouse model was calculated based on organ size and proximity measurements from 10 athymic mice, and all organs except bone and marrow (modeled as cylinders) were modeled as ellipsoids. By assuming a uniform dose distribution, both MIRD methods and Monte Carlo techniques were used to calculate organ self-dose for 90Y. Cross-organ dose was calculated using a model of overlapping and adjacent organs, in which the amount of overlap determined the amount of energy deposited in directly adjacent organs. Yoriyaz and Stabin (9) also used the concept of overlapping organs to generate a geometric mouse model. The Monte Carlo code, MCNP4A, was used to generate S factor values for selected organs (lungs to heart, liver to stomach) for 213Bi and 90Y. Further work was done by Muthuswamy et al. (10) for 131I, 186Re, and 90Y. Using slab, cylinder, and spheric geometry to generate computer models of marrow, this work extended the Hui model by considering all marrow spaces instead of just the femur and by adding 2 radionuclides. They concluded that, while it is critical to consider cross-organ dose for high-energy β-emitters such as 90Y, it is also of importance for lower-energy β-emitters. Most recently, Flynn et al. (11) used a composite model wherein the kidneys were resolved into the cortex and medulla, and other organs were represented as ellipsoids or cylinders; point-dose kernel convolution was used to obtain absorbed fractions.
In all but one of the works referenced, cross-organ φ or S factors were determined on the basis of geometric modeling of overlapping regions. In this work, murine S factors are generated on the basis of the anatomic structure of an actual mouse, as defined by noninvasive MRI using the previously developed 3-dimensional internal dosimetry package (3D-ID) (12) for 131I, 153Sm, 32P, 188Re, and 90Y. The radionuclides selected are of interest in radionuclide therapy (13–18). To facilitate absorbed dose calculations for radionuclides not included in this work, S factors and absorbed fractions have also been generated for 5 discrete monoenergetic electron energies ranging from 0.05 to 2 MeV.
MATERIALS AND METHODS
S factor calculations were performed using the software package 3D-ID by assigning unit cumulated activity to the liver, spleen, and right and left kidneys. Photon and electron dosimetry were considered separately by using appropriate kernels. The mean absorbed dose to each target organ then corresponds to the S factor value for that source–target organ combination. High-resolution MRI was used to define the murine anatomy.
MR Images
MR images of a disease-free female athymic mouse weighing 25 g were obtained on a 4.7-T small-animal MRI device using a custom-built coil. Fifteen T1-weighted, 1.5-mm-thick slices with a 0.5-mm gap were collected. The field of view for the acquisition was 25 mm. The MR images were acquired using a matrix size of 2562 over 15 slices, resulting in pixel dimensions of 0.01 × 0.01 × 0.2 cm. The 15-slice MR images were interpolated using Multiple Image Analysis Utility (MIAU), a previously described software package (19), to generate a 3-dimensional dataset with matrix dimensions of 2563.
The MR image data were read into 3D-ID, and anatomic segmentation was performed by drawing contours on individual 2-dimensional slices for the kidneys, spleen, and liver to define regions of interest (ROIs).
Point Kernels and Convolution
Point kernels were obtained from 2 sources: Monte-Carlo–derived β-dose point kernels for 90Y, 188Re, 131I, 153Sm, 32P, and 5 mono-energetic electrons (0.05, 0.1, 0.5, 1, and 2 MeV) from Simpkin and Mackie (20), and Monte-Carlo–derived photon dose kernels for 188Re, 131I, and 153Sm from Furhang et al. (21). Two techniques are used by 3D-ID for carrying out the convolution between a selected point kernel and an activity distribution image. The first approach is the previously described method of direct table lookup (12). However, for the extremely large datasets involved in the murine S factor calculations, the lookup method is inefficient in terms of time. Therefore, a second method has been implemented using a discrete fast Fourier transformation (dFFT) function (22), in which the entire image is convolved with the point kernel; this approach for calculating dose distributions was used in the past (23). Using the dFFT method places additional requirements on the image input data. Both image and kernel data must have the same dimensions, and the dimensions need to be isometric; image and kernel voxels must be cubic and have the same units and scaling.
In both techniques (table lookup and dFFT), it is necessary to calculate the self-dose for a voxel when source and target image voxels are spatially coincident. This calculation depends on the relationship of the voxel dimensions to the spacing of the point kernel tabulation. Assuming that there are n entries in a table, r0 is the smallest and rn is the largest distance over which the kernel is defined. For the β-kernels used in this work, rn is 2 times X90, which is the radius of a sphere absorbing 90% of the energy emitted by a point source at its center; for monoenergetic electrons, rn is approximately 1.2 times the continuous-slowing-down approximation range of the electron (24).
Three cases, dependent on the relationship of the voxel edge to the size of the point kernel, are considered when calculating voxel self-dose (Eq. 1). In the first case, the dimension of a single edge of the image voxel, s, is less than r0; the point kernel is inappropriate, and no dose calculation is performed. In the third case, s > rn, the total β or electron energy, Δ, is added to the voxel. The second case, r0 ≤ s ≤ rn, is more complex. It is necessary to calculate the portion of the electron energy that deposits within the volume of the voxel, a quantity no longer directly obtainable from the point kernel table. To calculate the total energy that should be assigned to the voxel, the point kernel is integrated from s to rn. This result is subtracted from the total energy, Δ, to yield the energy assigned to a single voxel. This is then divided by the voxel volume to yield the absorbed dose assigned to the voxel.
Mathematically, the voxel self-dose is given by:
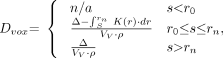 Eq. 1 where s is one edge of the image voxel, Δ is the total electron or β-particle energy (Gy kg/Bq-s), K(r) is the dose absorbed at radial distance r from point source (Gy/Bq-s), Vv is the voxel volume (cm3), r is the density (set to 1 g/cm3), and Dvox is the self-dose per unit cumulated activity in voxel (Gy/Bq-s).
Eq. 1 where s is one edge of the image voxel, Δ is the total electron or β-particle energy (Gy kg/Bq-s), K(r) is the dose absorbed at radial distance r from point source (Gy/Bq-s), Vv is the voxel volume (cm3), r is the density (set to 1 g/cm3), and Dvox is the self-dose per unit cumulated activity in voxel (Gy/Bq-s).
S Factor Calculation
A series of dose calculations were run in 3D-ID in which each defined ROI (i.e., liver, spleen, and left and right kidneys) was selected individually as the source organ. Each source organ was assumed to contain a uniform distribution of activity corresponding to unit total cumulated activity in each organ.
As noted above, to perform the dFFT convolution of the kernel function, K(r), with the image function, f(x,y,z), it is necessary that both functions have the same sampling frequency and the same dimensions. This is accomplished by resampling K(r) at distances corresponding to the dimensions of each voxel edge. In addition, K(r) is placed within a 3-dimensional matrix (u,v,w) with 0 values at distances greater than the largest distance in the original kernel table and symmetric with respect to the center placed at [u/2,v/2,w/2], giving K′(u,v,w). Because convolution in the spatial domain is complex multiplication in the frequency domain, the kernel and image functions are first transformed into the Fourier domain, multiplied together, and the inverse Fourier transform taken. The real portion of the result is extracted from the imaginary portion resulting in the function representing the dose distribution for the entire source image, f(D).
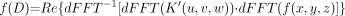 Eq. 2
Eq. 2
Mean dose was calculated for each target organ both for self-dose and for cross-organ dose in the third step of 3D-ID by assuming a cumulated activity of 1. Absorbed fractions (φt←s) are obtained using the following relationship:
 Eq. 3 where Mt is the mass of the target region and S(t←s) is the S factor for the specific source (s)–target (t) combination. In addition, selected dose distribution images were obtained to visualize the dose distribution for uniform radioactivity in the source organs.
Eq. 3 where Mt is the mass of the target region and S(t←s) is the S factor for the specific source (s)–target (t) combination. In addition, selected dose distribution images were obtained to visualize the dose distribution for uniform radioactivity in the source organs.
Validation
3D-ID was originally validated by calculating S factors using the standard human phantom geometry described by the MIRD Committee (12,25). The resulting S factors were then compared with S factors tabulated by the MIRD Committee (25). To ensure that the method is reliable in images with voxel dimensions much smaller than those found in human images and that its validity extends to the β-emitting radionuclides chosen for this work, the methodology was validated by comparison with previously published absorbed fractions for spheres of different radii (26,27). To perform this comparison, a series of spheric voxel phantoms with varying radii and voxel sizes were generated. The voxel phantoms were created using MIAU (19) by generating serial 2-dimensional images of circles of the appropriate radius, defined with a value of 1 inside the circle and 0 elsewhere. Spheres were created with radii ranging from 0.05 to 2.0 cm. To simulate the image pixel resolution from a variety of imaging devices, the spheres were generated within matrices of 643, 1283, and 2563. The 3-dimensional spheric datasets were then read into 3D-ID, and contours defining the outer edge of each sphere were drawn. The volume defined by the ROI was convolved with individual kernels as described above for each subject radionuclide, and S factor values were calculated for comparison with published Monte-Carlo–derived estimates.
RESULTS
Organ Volumes
Organ volumes obtained from the ROIs used in the dose calculation are shown in Table 1. Comparisons with organ volumes used in the Hui model (8) show differences of 32% in liver, 20% in combined kidney volume, and −40% in the spleen.
Volumes from 3D-ID ROI Analysis
S Factors and Absorbed Fractions
Tables 2 and 3 list the β-radionuclide and monoenergetic electron S factor values, respectively. Corresponding absorbed fraction values are shown in Tables 4 and 5. Table 6 shows 131I, 153Sm, and 188Re S factors and absorbed fractions for separately calculated photon contributions. The β-absorbed fractions are compared with previously published murine absorbed fractions for 131I and 90Y (8,9) in Table 7. Generally, good agreement was seen with previous estimates. Direct comparisons for the kidneys cannot be made because estimates for individual kidneys were not reported in those studies. The errors associated with the earlier estimates were estimated to be 5%–10% (8) and were deemed not significant compared with the gross error of ignoring cross-organ β-doses. Example absorbed dose distribution images and dose volume histogram are shown in Figures 1 and 2.
Three-panel composite image from dose histogram displays module of 3D-ID. (A) Transverse slice of mouse MR image with contours shown for spleen (green), right kidney (yellow), left kidney (red), and liver (orange). (B and C) Corresponding transverse slices from β-dose distribution images of 131I and 90Y, respectively. Also shown in panels B and C are isodose curves at 1%, 5%, 50%, and 90% levels. Bulge in 1% isodose level shows effect from 0.5-mm-distant portions of spleen. However, as seen in 131I image, even 1% level does not irradiate nearest organ (left kidney) compared with 90Y image, which shows significant portion of left kidney receiving dose from spleen at 1% isodose level.
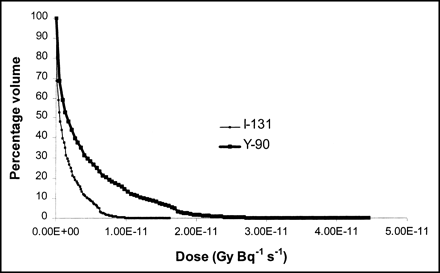
Dose volume histogram of liver to right kidney for 131I (light line) and 90Y (heavy line). It can be observed in dose volume histogram that β-dose effect of 90Y extends over longer range.
β-Only S Factors (Gy/Bq s) for 5 Radionuclides
S Factors (Gy/Bq s) for 5 Monoenergetic Electrons
β-Only Absorbed Fractions for 5 Radionuclides
Absorbed Fractions for 5 Monoenergetic Electrons
Photon-Only S Factors and Absorbed Fractions for 131I, 153Sm, and 188Re
Comparison of 3D-ID Calculated β-Absorbed Fractions with Previously Published Values
Validation
3D-ID–generated S factors were compared with values published by Bardies and Chatal (26) for all 5 radionuclides at 3 matrix sizes and for radii ranging from 0.05 to 2 cm. Spheres generated within 643 matrices showed differences ranging from 5% to 18%; corresponding values for 1283 and 2563 matrices were 2%–12% and 1%–10%, respectively. Figure 3 depicts the comparison across different radii for a 2563 matrix for 131I and 90Y. As shown in the figure, selected comparisons for these 2 radionuclides were also made using data published by Siegel and Stabin (27).
Comparison of β S factor values in spheres of different masses calculated using different methods. S factors derived from 3D-ID calculations are denoted by circular symbols and are compared with Bardies and Chatal (26), denoted by square symbols, and Siegal and Stabin (27), indicated by triangular symbols. Top graph, indicated by dashed line and unfilled symbols, plots S factor values for 90Y, whereas lower graph, indicated by solid line and solid symbols, plots S factors value comparisons for 131I. It can be seen in graph that values generally fall on same line, with best coincidence seen in middle of graph and less coincidence seen on either end. Sphere of smallest radii shows most disparity of values as calculated by 3 methods.
DISCUSSION
Using MR images of a mouse, we have generated β- and photon S factors for liver, spleen, and kidneys by point kernel convolution for several radionuclides and also for a series of monoenergetic electrons. The latter may be used to derive S factor values for radionuclides not listed in this work. The calculation for the photon contribution to the S factors for 131I, 153Sm, and 188Re showed that, whereas photon self-dose in each of these 3 cases accounted for less than 3% of the total S factor value, the cross-organ absorbed dose was significant. Therefore, a separate photon table (Table 6) was included so that the different types of radiation may be considered separately or in combination as needed.
In addition, images of the absorbed dose distribution for unit cumulated activity in each volume, dose-volume histograms, and isodose contours were generated and show the impact of emission energy and pathlength.
The differences between the longer- and shorter-range β-emitters can be seen visually in Figure 1, where the more limited range of 131I shows the dose distribution to be mainly within the boundaries of the organs, as opposed to the image of the 90Y dose distribution, where the effect of the dose can be seen to spread out from the organ into the surrounding tissue areas. Comparison of current self-dose S factors with S factors derived assuming complete absorption of emitted energy gave a maximum difference of 190% for 90Y spleen self-dose. Correspondingly, cross-organ S factors for longer-range β-emitters, 90Y, 188Re, and to a lesser extent, 32P, are greater than for the short-range emitters.
The ROI-derived volumes for liver and kidneys were 32% and 20% greater than the volumes reported in the model by Hui et al. (8). The spleen volume was 40% lower, suggesting that the organ volume differences are not the result of using different-sized animals in the 2 calculations. These differences in organ volumes may be the result of estimates obtained in vivo (by MRI) versus estimates obtained ex vivo (8). Despite these differences in organ mass, good agreement between 3D-ID–derived and published S factors was found in the cases where such comparison was possible.
Validation studies showed that agreement between Monte Carlo–derived S factors and those based on voxelized phantoms generally improved with increasing matrix resolution. The murine S factors were, therefore, calculated at the 2563 resolution.
Absorbed dose images obtained for unit source organ cumulated activity show that the cross-organ absorbed dose for β-emissions is largely confined to a small portion of the target organ volume adjacent to the source organ. This high level of nonuniformity in absorbed dose suggests that absorbed dose calculations using cross-organ S factor values are not likely to predict potential biologic effects and that suborgan or 3-dimesional–based dosimetry would be required.
CONCLUSION
In this work, we report murine S factor values for 5 radionuclides. By validation studies, we demonstrated that the 3D-ID software package, originally designed for human, patient-specific dosimetry may be applied at the smaller resolutions found in animal imaging. In addition, we have generated absorbed fractions for 5 monoenergetic electrons that should be useful for estimating the dose to the organs of the liver, kidney, and spleen in mice for radionuclides other than those explicitly reported.
Acknowledgments
This work was supported by National Institutes of Health grants RO1 CA62444, PO1 CA33049, and R24 CA83084 and Department of Energy grant DE-FG02-86ER-60407.
Footnotes
Received Jul. 15, 2002; revision accepted Jan. 20, 2003.
For correspondence or reprints contact: Katherine S. Kolbert, MS, Department of Medical Physics, Memorial Sloan-Kettering Cancer Center, 1275 York Ave., New York, NY 10021.
E-mail: kolbertk{at}mskcc.org