Non-invasive estimation of hepatic glucose uptake from [¹⁸F]FDG PET images using tissue-derived input functions

Abstract

Purpose

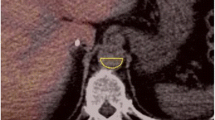
The liver is perfused through the portal vein and hepatic artery. Quantification of hepatic glucose uptake (HGU) using PET requires the use of an input function for both the hepatic artery and portal vein. The former can be generally obtained invasively, but blood withdrawal from the portal vein is not practical in humans. The aim of this study was to develop and validate a new technique to obtain quantitative HGU by estimating the input function from PET images.

Methods

Normal pigs (n = 12) were studied with [¹⁸F]FDG PET, in which arterial and portal blood time-activity curves (TAC) were determined invasively to serve as reference measurements. The present technique consisted of two characteristics, i.e. using a model input function and simultaneously fitting multiple liver tissue TACs from images by minimizing the residual sum of square between the tissue TACs and fitted curves. The input function was obtained from the parameters determined from the fitting. The HGU values were computed by the estimated and measured input functions and compared between the methods.

Results

The estimated input functions were well reproduced. The HGU values, ranging from 0.005 to 0.02 ml/min per ml, were not significantly different between the two methods (r = 0.95, p < 0.001). A Bland-Altman plot demonstrated a small overestimation by the image-derived method with a bias of 0.00052 ml/min per g for HGU.

Conclusion

The results presented demonstrate that the input function can be estimated directly from the PET image, supporting the fully non-invasive assessment of liver glucose metabolism in human studies.

Appendix

A model function for hepatic input function for ¹⁸FDG was created, by assuming a three-compartment model, in which the tracer is administered in a rectangular form and diffuses bidirectionally between arterial blood and whole-body peripheral tissue compartments. Part of the tracer is metabolized and accumulated in the third compartment. Differential equations for the model function (C _I(t)) can be expressed as;

$$ \frac{{dC_I \left( t \right) }}{dt}=\frac{dF}{dt} - K_E C_I \left( t \right) + K_I C_{WB} \left( t \right) $$

(5)

$$ \frac{{dC_{WB} \left( t \right)}}{dt} = K_E C_I \left( t \right) - K_I C_{WB} \left( t \right) - K_M C_{WB} \left( t \right) $$

(6)

$$ \begin{gathered} \frac{dF}{dt} = A\quad \quad \left( {t_1 \le t \le t_2 } \right) \hfill \\ \quad \quad \quad 0\quad \quad \left( {elsewhere} \right) \hfill \\ \end{gathered} $$

(7)

where t ₁ assumes the appearance time of administered tracer and t ₂-t ₁ represents the administration duration, A is scalar of input function. The equation F (Eq. 7) represents the bolus administration of tracer in the rectangular form with duration t ₂-t ₁. C _WB(t) is the expected tracer concentration in whole-body peripheral tissues, K _E and K _I are bidirectional tracer diffusion rates between blood and peripheral tissue compartments, respectively, and K _M is the metabolic rate of the tracer in assumed whole body. Solving Eq. 6 for C _WB gives:

$$ C_{WB} \left( t \right) = K_e e^{{ - \left( {KI + KM} \right) \cdot t}} \int_0^t {C_I \left( \tau \right)e^{{\left( {KI + KM} \right) \cdot \tau }} d\tau } $$

(8)

The sum of Eq. 5 and a × Eq. 6 generates:

$$ \frac{{d\left( {C_I \left( t \right) + aC_{WB} \left( t \right)} \right) }}{dt}=\frac{dF}{dt} + \left( {a - 1} \right)K_E \left( {C_I + aC_{WB} } \right) $$

(9)

where

$$ a = {{\left( {{{{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E - 1 + K_M }}} \right. } {K_E - 1 + K_M }}} \mathord{\left/ {\vphantom {{{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E - 1 + K_M }}} \right. } {K_E - 1 + K_M }}} {K_E }}} \right. } {K_E }}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E - 1 + K_M }}} \right. } {K_E - 1 + K_M }}} \mathord{\left/ {\vphantom {{{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E - 1 + K_M }}} \right. } {K_E - 1 + K_M }}} {K_E }}} \right. } {K_E }}} \right)} 2}} \right. } 2} + \sqrt {{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E }}} \right. } {K_E }} + {{\left( {{{{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E - 1 + K_M }}} \right. } {K_E - 1 + K_M }}} \mathord{\left/ {\vphantom {{{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E - 1 + K_M }}} \right. } {K_E - 1 + K_M }}} {K_E }}} \right. } {K_E }}} \right)^2 } \mathord{\left/ {\vphantom {{\left( {{{{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E - 1 + K_M }}} \right. } {K_E - 1 + K_M }}} \mathord{\left/ {\vphantom {{{{K_I } \mathord{\left/ {\vphantom {{K_I } {K_E - 1 + K_M }}} \right. } {K_E - 1 + K_M }}} {K_E }}} \right. } {K_E }}} \right)^2 } 4}} \right. } 4}} $$

(10)

Thus,

$$ C_I \left( t \right) + aC_{WB} \left( t \right)=\frac{dF}{dt} \otimes \exp \left( { - \left( {1 - a} \right)K_E t} \right) $$

(11)

where ⊗ indicates convolution integral. Substitution of C _WB from Eq. 8 into Eq. 11 after multiplying e ^(KI+KM)·t gives:

$$ e^{{\left( {KI + KM} \right) \cdot t}} C_I \left( t \right) + aK_E \int_0^t {C_I \left( \tau \right)e^{{\left( {KI + KM} \right) \cdot \tau }} d\tau } = e^{{ - \left( {1 - a} \right)Ke \cdot t + \left( {KI + KM} \right) \cdot t}} \int_0^t {\frac{dF}{dt}e^{{\left( {1 - a} \right)Ke \cdot t}} d\tau } $$

(12)

Differentiation with respect to t after arrangement gives:

$$ \left( {\frac{{K_I }}{a} + K_E } \right)C_I \left( t \right) + \frac{{dC_I \left( t \right)}}{dt} = \frac{{K_I }}{a}e^{{ - \left( {1 - a} \right)Ke \cdot t}} \int_0^t {\frac{dF}{dt}e^{{\left( {1 - a} \right)Ke \cdot t}} d\tau } + \frac{dF}{dt} $$

(13)

Thus,

$$ C_I \left( t \right) = \frac{{K_I }}{a}\,e^{{ - \beta \cdot t}} \int_0^t {e^{{Ke \cdot \left( {a - 1} \right) \cdot T + \beta \cdot T}} \int_0^T {\frac{dF}{dt}} e^{{Ke \cdot \left( {1 - a} \right) \cdot \tau }} d\tau } dT + e^{{ - \beta \cdot t}} \int_0^T {\frac{dF}{dt}} e^{{Ke \cdot \beta \cdot \tau }} d\tau $$

(14)

where β=(K _I /a+K _E ). Solving Eq. 14, we obtain:

$$ \begin{gathered} \begin{array}{*{20}c} {C_{\text{I}} \left( t \right)~ = ~0.\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( {t < t_1 } \right)} \\ { = A\left[ {\frac{{1 - \exp \left( {\beta \left( {t_1 - t} \right)} \right)}}{\beta } + \frac{{\alpha \left( {1 - \exp \left( {\beta \left( {t_1 - t} \right)} \right)} \right)}}{{a\left( {1 - a} \right)\beta }} - \frac{{\alpha \left( {\exp \left( {K_E \left( {1 - a} \right)\left( {t_1 - t_2 } \right)} \right) - \exp \left( {\beta \left( {t_1 - t} \right)} \right)} \right)}}{{a\left( {1 - a} \right)\gamma }}} \right]\quad \quad \quad \left( {t_1 < t < t_2 } \right)} \\ { = \left[ {A\frac{{\exp \left( {\beta \left( {t_2 - t} \right)} \right) - \exp \left( {\beta \left( {t_1 - t} \right)} \right)}}{\beta } + \frac{{\alpha \left( {1 - \exp \left( {\beta \left( {t_1 - t_2 } \right)} \right)} \right)}}{{a\left( {1 - a} \right)\beta }} + \frac{{\alpha \left( {\exp \left( {K_E \beta \left( {t_1 - t_2 } \right)} \right) - \exp \left( {\beta \left( {t_1 - t_2 } \right)} \right)} \right)}}{{a\left( {1 - a} \right)\gamma }} + \frac{{\alpha \left( {\exp \left( {K_E \left( {1 - a} \right)t_2 } \right) - \exp \left( {K_E \left( {1 - a} \right)t_1 } \right)} \right)\left. {\left( {\exp \left( {K_E \left( {1 - a} \right)t} \right) - \exp \left( {\gamma t_2 - \beta t} \right)} \right)} \right)}}{{a\left( {1 - a} \right)\gamma }}} \right]\quad \quad \quad \left( {t > t_2 } \right)} \\ \end{array} \hfill \\ ~ \hfill \\ ~ \hfill \\ ~ \hfill \\ \end{gathered} $$

(15)

where α= K _I /K _E and γ=(K _I /a+aK _E ).