Visual Abstract
Abstract
In radiopharmaceutical therapy, dosimetry-based treatment planning and response evaluation require accurate estimates of tumor-absorbed dose. Tumor dose estimates are routinely derived using simplistic spherical models, despite the well-established influence of tumor geometry on the dosimetry. Moreover, the degree of disease invasiveness correlates with departure from ideal geometry; malignant lesions often possess lobular, spiculated, or otherwise irregular margins in contrast to the commonly regular or smooth contours characteristic of benign lesions. To assess the effects of tumor shape, size, and margin contour on absorbed dose, an array of tumor geometries was modeled using computer-aided design software, and the models were used to calculate absorbed dose per unit of time-integrated activity (i.e., S values) for several clinically applied therapeutic radionuclides (90Y, 131I, 177Lu, 211At, 225Ac, 213Bi, and 223Ra). Methods: Three-dimensional tumor models of several different shape classifications were generated using Blender software. Ovoid shapes were generated using axial scaling. Lobulated, spiculated, and irregular contours were generated using noise-based mesh deformation. The meshes were rigidly scaled to different volumes, and S values were then computed using PARaDIM software. Radiomic features were extracted for each shape, and the impact on S values was examined. Finally, the systematic error present in dose calculations that model complex tumor shapes versus equivalent-mass spheres was estimated. Results: The dependence of tumor S values on shape was largest for extreme departures from spherical geometry and for long-range emissions (e.g., 90Y β-emissions). S values for spheres agreed reasonably well with lobulated, spiculated, or irregular contours if the surface perturbation was small. For marked deviations from spherical shape and small volumes, the systematic error of the equivalent-sphere approximation increased to 30%–75% depending on radionuclide. The errors were largest for shapes with many long spicules and for spherical shells with a thickness less than or comparable to the particle range in tissue. Conclusion: Variability in tumor S values as a function of tumor shape and margin contour was observed, suggesting use of contour-matched phantoms to improve the accuracy of tumor dosimetry in organ-level dosimetry paradigms. Implementing a library of tumor phantoms in organ-level dosimetry software may facilitate optimization strategies for personalized radionuclide therapies.
Tumors are inherently variable, and tumor geometric characteristics including volume, shape (e.g., ovoid or irregular), margin morphology (e.g., circumscribed, lobulated, or spiculated), and composition (e.g., calcifications) are routinely assessed as anatomic imaging biomarkers or radiomic features (1,2). For tumors and normal organs, geometric features and composition influence the absorbed doses received from therapeutic radiopharmaceuticals. Over the last 50 y, human computational phantoms have evolved with tools for simulating radiation transport. Software programs implementing phantoms with anatomically realistic 3-dimensional organ shapes are now in widespread use for organ-level internal dosimetry (3–6). In contrast to organs, tumors are generally modeled as soft-tissue spheres of equivalent mass in organ-level dosimetry workflows—that is, tumor shape, margin morphology, and composition are rarely, if ever, incorporated into tumor dosimetry analyses.
A principal barrier to incorporation of these factors has been the lack of computational phantoms representative of shapes and compositions other than soft-tissue spheres and ellipsoids (7,8). In a recent study, Olguin et al. comprehensively investigated the dependence of tumor self-dose on tissue composition using a series of spheroid phantoms comprising various combinations of soft-tissue and mineral bone content (8). This study illustrated that assuming soft-tissue composition for highly mineralized tumors may translate to relative errors exceeding 80% in tumor dose estimates. Absorbed doses per unit of time-integrated activity (i.e., S values) derived from this study were built into the new MIRDcalc dosimetry software to enable routine consideration of tumor composition in tumor dosimetry calculations (5). The present study expands on previous work (8) to more comprehensively investigate the effect of tumor shape and margin contour on tumor self-dose.
In the present work, a procedural noise-based method for generating mesh-type representative tumor computational phantoms is described. Using this method, a library of tumor phantoms of differing volume, shape, and margin contour was generated. Using the library, S values for several therapeutic radionuclides were computed to provide insights into the influence of shape and contour on tumor-absorbed dose. Finally, practical application of such a library in routine clinical organ-level dosimetry workflows is discussed.
MATERIALS AND METHODS
Tumor Modeling
The 3-dimensional modeling software Blender (version 3.0.0; Blender Foundation) was used to generate the tumor phantom library (Fig. 1). Blender’s icosphere geometric primitive (a triangulated spherical surface) was used as the base mesh from which all other library members were generated. Specific procedures for generating additional shapes and contours are described below.
Tumor phantom library scaled to constant Feret diameter. Relevant parameters defining each shape or contour are provided on axis gridlines. C = coverage parameter; D = density parameter; L = length parameter; T = relative shell thickness; Z = z-axis scale factor.
Spheroids
Spheroid shapes were generated by scaling the unit icosphere along the z-axis. Two oblate spheroids were generated using z-axis scale factors of 0.25 and 0.5. Two prolate spheroids were generated using z-axis scale factors of 2.0 and 4.0. Isotropic scaling was then used to generate similar spheroids of a range of volumes.
Spherical Shells
Spherical shells were modeled to approximate lesions with target-expressing malignant cells concentrated at the periphery (e.g., lesions with central necrosis). These were generated using a unit icosphere and a smaller icosphere. The latter icosphere partitions the phantom into an inner spherical core and an outer spherical shell or annulus. The relative shell thicknesses T were defined in relation to the outer (i.e., overall tumor) radius R: T = 0.2, 0.4, 0.6, or 0.8 R. Isotropic scaling was then used to generate similar spherical shells of a range of volumes.
Lobulated, Spiculated, and Irregular Contours
Tumor surface contours were generated by radially displacing the vertices of the icosphere. Let r be a vertex on the unit icosphere centered on the origin. Let 
be a function for the relative radial displacement of each vertex; the range of f is 0–1. A point on the surface of the deformed shape is defined as…
where L is a scaling factor for controlling the magnitude of the displacement.
There are numerous basis functions that might be used to determine suitable values of f to approximate tumor contours. Here, Worley noise (9), a procedural noise function implemented in Blender’s Voronoi texture node, was used. Worley noise is often used in 3-dimensional design to simulate structures with discernable boundaries, such as pebbles, cell clusters, soap bubbles, or other self-organizing structures. In the present case, the Worley noise field was generated by seeding random points in 3-dimensional space and evaluating the Euclidean distance to the closest random point as a function of position. The range of distances in the noise field are then normalized to range between 0 and 1 (i.e., a relative noise field). Optionally, thresholding, smoothing, or other manipulations can be applied to the field before normalization. The values of f are obtained by sampling the relative noise field at each vertex. The positions of the vertices in the deformed shape then follow from Equation 1. Finally, the shape can be scaled to an arbitrary volume by isotropic scaling.
Our method for generating tumor surface contours is based on 3 central inputs that parameterize the Worley noise field and a fourth isotropic scaling factor. The first parameter, L, is discussed above. Second, a density parameter, D, is varied to control the number of bump or spike projections from the sphere surface. Third, a coverage threshold parameter, C, influences the fraction of the sphere surface that can be perturbed. Finally, an isotropic scaling factor, I, is used to scale the tumor to an arbitrary volume:
where V is the desired volume and V0 is the initial volume. Alternatively, the tumor may be scaled to an arbitrary Feret diameter (10,11), F, which represents the greatest dimension of a tumor (formally, the maximal pairwise Euclidean distance between the surface mesh vertices). F0 is the Feret diameter of the initial (i.e., nonscaled) shape.
Notably, by adjustment of the parameters, the morphologic characteristics of the output shape can be made to mimic tumor margin pathology including lobulations, microlobulations, spiculations, or irregularity (Fig. 2). A range of representative margin contours has been generated using parameter combinations guided by clinical experience and the literature. Readers themselves may generate tumor phantoms by adjusting the node input parameters in the Blender file as described in the supplemental material (available at http://jnm.snmjournals.org).
Method for generating representative lobulated, spiculated, or irregular tumor phantoms. (A and B) Contours are parameterized by length parameter L, density parameter D, and threshold parameter C (A), which together determine 3-dimensional Worley noise field (B). (C) Noise field is sampled at vertices of unit icosphere. (D) Vertices are radially displaced on basis of value sampled from noise field. (E) Shape is then isotropically scaled to desired volume.
The tumor surface meshes were exported from Blender in stereolithography (*.stl) format and converted to tetrahedral meshes with Tetgen (12) (using the -pAY command line arguments) in preparation for S-value computations. The volumes of the n tetrahedral elements comprising the volumetric tumor mesh were summed to yield V0, namely…
where 
, 
, 
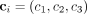, and 
. These are position vectors defining the vertices of the ith tetrahedral element.
The surface area of each phantom was computed by summing the n triangular elements comprising the surface of the phantoms:
where ai, bi, and ci are position vectors defining the vertices of the ith triangle.
S-Value Computation
In the MIRD dosimetry formalism, the S value 
(Gy/Bq·s) (13) quantifies the absorbed dose 
(Gy) to a radiosensitive target 
per unit of time-integrated activity 
(Bq·s) of radionuclide 
in source 
:
In the present case, tumor self-dose (i.e.,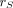 
= 
) was considered and the distribution of activity in the tumor was assumed to be spatially uniform.
For each tumor phantom, self–S values for 3 β-particle emitters (90Y, 131I, and 177Lu) and 4 α-emitters or α-generating decay chains (225Ac, 213Bi, 223Ra, and 211At) were computed using PARaDIM software (3). S values for the radionuclides with radioactive progeny were computed separately. Relevant decay information for each radionuclide are provided in Table 1.
Radionuclides Considered in Present Study
PARaDIM used PHITS, version 3.24 (14), for Monte Carlo simulations. Each calculation used the PARaDIM default parameters for physical models in PHITS, which used the International Commission on Radiological Protection publication 107 library for decay spectra (15), the PHITS-EGS5 method for treatment of multiple scattering, explicit treatment of fluorescent x-rays, consideration of Rayleigh and incoherent scattering, and consideration of electron-impact ionization. Sampling was used to determine bremsstrahlung polar angles, electron–positron pair polar angles, and distribution of photoelectrons. A cutoff energy of 1.0 keV were used for electrons and photons. Soft-tissue elemental composition and density, as defined in International Commission on Radiation Units and Measurements report 46 (16), were the attributes assigned to the tetrahedral mesh tumor region and surrounding material. A sufficient number of particle histories was run such that the relative statistical uncertainties in the S values were less than 1%. For the β-particle emitters, the full β-spectrum was used. For all radionuclides, the contributions of monoenergetic electrons (e.g., conversion and Auger or Coster–Kronig electrons) were included.
The S-value calculations were repeated for different tumor volumes using the phantom scaling function in PARaDIM. Specific volumes were selected by sampling values for the equivalent-sphere diameter at semiregular intervals. For an arbitrary tumor shape of the same composition, the radius of the equivalent-mass sphere is 
, where V is the volume of the shape. The equivalent-sphere diameter is 2Req. The range of sampled values for the equivalent-sphere diameter was deemed clinically relevant based on concordance with the eighth edition TNM staging system (Table 2) (17,18).
Tumor Volumes Used to Compute S Values in This Study
Comparative Evaluation
Of interest here are the systematic errors that arise when tumors with various morphologic characteristics are modeled as equivalent-mass spheres in self-absorbed dose calculations. The percentage error in the S value is defined as follows:
where Stumor is the S value for the actual tumor shape and Sequivalent sphere is the self–S value for the icosphere (representing a sphere) of equivalent mass.
Validation of S-Value Calculations
S values computed for the icosphere were compared with those for spheres obtained from the new MIRDcalc dosimetry software tool (5,8) as a validation measure.
Radiomic Shape Features
The imaging subfield of radiomics involves the identification of quantitative features in digital images that may be predictive of tumor pathophysiology; one large class of radiomic features includes shape- and size-based features (2,10,11,19–21). We hypothesized that these features may inform dosimetric relationships—namely, the influences of tumor shape on the S values and the systematic errors in S values associated with the equivalent-sphere approximation. Eight shape features, in addition to the parameters defining our tumor shape library, were extracted. Potential correlations among the shape features and S values were then considered. Definitions and descriptions of each feature are provided in Table 3.
Radiomic Features Derived Across Tumor Phantom Library
RESULTS
S values for 90Y, 131I, 177Lu, 225Ac, 213Bi, 223Ra, 211At, and decay chain members, when applicable, are provided in Supplemental Tables 1–19 for each phantom in the tumor library. The contributions of radioactive progeny are tabulated separately from the parent.
Figures 3 and 4 demonstrate that the standard practice of defining lesions as equivalent-mass spheres systematically overestimates the absorbed dose and, further, that the magnitude of the error is influenced by the radionuclide, shape, volume, and margin contour. In the case of high-energy β-emitters (e.g., 90Y), relative errors of up to 75% were observed for spiculated contours with high values of L and up to 68% for thin spherical shells (Fig. 3). Relative errors for all isotopes are provided in Supplemental Tables 20–38. Radiomic features associated with each shape are provided in Supplemental Tables 39–49. Figure 4 provides insight on how the relative errors in the equivalent-sphere S values trend with different radiomic features and provides an indication of the potential magnitude of dosimetric error when the equivalent-sphere approximation is applied for specific radionuclides. For example, for the α-emitter 211At, relative errors were less than 10% across the entire shape library for volumes of more than 0.2 cm3, sphericity values of more than 0.2, and area-to-volume ratios of less than 150. Over the present shape library, the relative errors tended to increase with surface area–to–volume ratio and tended to decrease with increasing sphericity, volume, and Feret diameter. None of the examined radiomic features yielded quantitatively predictive relationships with S values or with their relative errors.
Relative error in absorbed dose if equivalent mass spheres are used to approximate various representative nonspheric tumors. Req values on abscissa are centimeters; corresponding volumes can be obtained from Table 2. C = coverage parameter; D = density parameter; L = length parameter; T = relative shell thickness; Z = z-axis scale factor.
Correlation of relative errors with radiomic shape features for various shapes and radionuclides. Progeny are not included for 211At.
Validation
S values obtained from MIRDcalc for soft-tissue spheres agreed within 2.5% of the S values derived in this work for the icosphere geometry (Supplemental Fig. 1). The differences may be attributed to subtle differences in geometry definition or simulation settings.
DISCUSSION
A library of tumor computational phantoms of various shapes and contours, created using 3-dimensional design software, has been assembled to improve accuracy in tumor dosimetry.
Envisioned Practical Use
Radionuclide S values were generated across the library for tumor self-absorbed dose calculations via a shape lookup table. In general, the dose calculations will involve 3 steps: shape matching, time-integrated activity estimation, and absorbed dose calculation. The latter 2 steps are commonly performed using organ-level dosimetry software (4–6), but these software applications currently support only spherical phantoms; the S-value database generated in this work might be integrated into these existing software tools to enhance their versatility for tumor dosimetry.
Shape-Matching Considerations
The library phantom that is the closest match should be identified, guided by quantitative or semiquantitative analysis of anatomic images and the visual interpretation and clinical judgment of the users. Some characteristics for appearance-based semiquantitative matching might include lobule or spicule count, apparent spicule length, or apparent Feret diameter. Quantitative features might be extracted via image segmentation and compared with feature values extracted from the library phantoms to determine the optimal match. The uncertainty associated with each feature might be estimated to determine which features to prioritize. For example, the lesion volume can be difficult to estimate accurately if features such as spiculations are not well resolved or if only planar images are available; in that case, the Feret diameter may be a better indicator of the true tumor S value. Finally, if several phantoms provide a reasonable match to the tumor, their corresponding S values might be averaged, or alternatively, an interpolation scheme might be applied.
Importantly, the techniques for visualizing the library phantoms and the tumor should be congruent. For example, CT slices should be compared with corresponding slices of the phantoms, whereas projections of the phantoms would be more appropriate comparators for CT maximum-intensity projections, radiographic projections such as mammography, or digitally reconstructed radiographs (Fig. 5).
When matching phantom to image data, shape visualization technique should be appropriate for imaging modality. (A) Tumors imaged with different imaging modalities. (B and C) Slice (B) and rendered projection (C) views of most closely matching phantoms from library, assessed by authors. (D) Entire phantom library displayed for reference. (Lung tumor CT images adapted from (23); breast tumor mammography image adapted from (24).)
The method for generating the tumor phantom library was designed to be versatile but with minimal parameter inputs, such that the library can be systematically expanded if it proves useful. Through variation of up to 4 parameters, representative tumor phantoms can be generated with characteristic features—size, shape, and margin contour—observable in planar or tomographic anatomic images or expected on the basis of knowledge of the pathology. The Blender file used to generate the library phantoms has been provided in the supplemental materials. This enables one to optimize each parameter to more closely replicate observed tumor features. In that case, several Monte Carlo particle transport codes can compute the S value with the output shape, including GEANT4, PHITS, and MCNP.
Advantages and Limitations
There cannot realistically be a 1:1 correspondence between a representative phantom and a real tumor, and the approach is somewhat subjective. However, by accounting for the salient features that influence the mean absorbed dose, a more accurate result should be achievable than is possible with the first-order equivalent-mass-sphere approximation that has typically been used.
Ideally, one would account for the unique characteristics of each lesion in dosimetry calculations, including lesion size, lesion shape, lesion contour, intratumoral heterogeneity, the dynamics of radiopharmaceutical distribution, and their collective impact on the dose distribution. Recent progress toward this goal includes advancements in nuclear imaging instrumentation, image segmentation, image registration, and software developments that enable voxel-level dosimetry calculations. One inherent limitation of traditional voxel-level dosimetry is that the accuracy ultimately depends on the resolution of the nuclear imaging modality, which at best approaches 5 mm (clinical PET); this can be insufficient to capture activity concentration gradients or absorbed dose gradients that are dosimetrically relevant (22). The resolution of anatomic imaging modalities is far superior, with submillimeter resolution achievable with modern CT and MR scanners that accompany modern PET and SPECT systems; especially for high-contrast scenarios (e.g., lung nodules), these anatomic imaging modalities might provide lesion contour information to inform selection of a representative tumor phantom from our library. Moreover, for metastatic or multifocal disease, the concept of the index tumor is commonly used, wherein a representative lesion (usually, the largest lesion) is presumed to determine the overall clinical behavior of the disease. An analogous strategy might be applied for dosimetric evaluation, wherein the morphology of the index tumor is presumed to dictate the shape and contour of other foci. This strategy might have merit when the margin morphology of an index tumor is resolvable by the anatomic imaging modality or can be plausibly inferred from other available anatomic information such as biopsy specimens, a surgically resected lesion, or correlations with other biomarkers. However, the accuracy of such inferences would need to be rigorously evaluated before use in practice.
CONCLUSION
A tumor phantom library was generated to enable integration of tumor shape and contour into routine tumor dosimetry calculations. Using the library, we have shown that mean absorbed doses are systematically overestimated for tumors when the equivalent-sphere approximation is applied to tumors with distinctly different shapes. Integrating the phantom library within internal dosimetry software would enable greater versatility and might increase the accuracy of tumor-absorbed dose estimates.
DISCLOSURE
Funding support was received from NIH P30 CA008748 and NIH U01 EB028234. Simone Krebs is supported in part by NIH R37 CA262557 and P50 CA192937. No other potential conflict of interest relevant to this article was reported.
KEY POINTS
QUESTION: How accurate are the spherical tumor models implemented in common organ-level internal dosimetry software, and can these models be improved?
PERTINENT FINDINGS: Using a library of computational tumor phantoms that recapitulate dosimetrically relevant tumor morphology, we found that spherical tumor models may systematically overestimate the absorbed dose by over 75% for certain therapeutic radionuclides.
IMPLICATIONS FOR PATIENT CARE: Tumor phantom libraries might improve software programs for organ-level dosimetry by allowing the morphology of the real tumor to be accounted for in dosimetry calculations, thereby translating to dosimetry estimates that are more tumor-specific.
Footnotes
Published online Dec. 8, 2022.
- © 2023 by the Society of Nuclear Medicine and Molecular Imaging.
REFERENCES
- Received for publication September 13, 2022.
- Revision received November 29, 2022.
