Fundamental Statistical Concepts in Clinical Trials and Diagnostic Testing

NRG-HN006 TRIAL

There is a lack of consensus in the head and neck cancer community on how to treat patients with early-stage oral cancer (1,2). NRG-HN006 (NCT04333537) randomizes T1–2N0M0 oral cavity patients with negative ¹⁸F-FDG PET or PET/CT findings to elective neck dissection (END) or sentinel lymph node biopsy (SLNB). The coprimary objectives assess noninferiority in disease-free survival and superiority in quality of life.

For the SLNB arm, the primary tumor is injected with a radiotracer that travels to the cervical lymph nodes. The first echelon of nodes that are localized by the radiotracer represent those most likely to harbor metastatic disease. The SLN can then be biopsied when the primary tumor is excised. Typically, the incision made in the neck is smaller than normal, and rather than having to dissect the entire lymph node basin, as with END, less surgical manipulation is required to remove a small number of lymph nodes. Pathologic examination is then focused on nodes with the highest likelihood of harboring disease, rather than on many nodes harvested from END. An important research question is whether there is a significant difference in the performance of radiotracers in terms of the false-negative rate (FNR). The FNR, to be described later, corresponds to a negative SLNB result in a patient who subsequently develops metastatic lymph nodes without recurrence at the primary site (3).

HYPOTHESIS TESTING

Clinical trials are designed around a hypothesis that is used to determine the trial’s primary objective. Trials are conducted within a sample, a subset of the population of interest. Statistics are used to summarize the sample and estimate an unknown population parameter, a number summarizing the population (Table 1) (4). Hypothesis tests are based on a null hypothesis, H₀, and an alternative hypothesis, H_A. The H₀, which is the hypothesis being tested, is a very specific statement about a parameter of the population. The H_A is a broader statement that pairs with the H₀ but is mutually exclusive from it. The H_A is sometimes referred to as the research hypothesis because it states, in statistical terms using parameters, the primary hypothesis of the trial. For example, if the FNRs were compared between 2 radiotracers (Rad1 and Rad2) in NRG-HN006, H₀ and H_A would be…Hypothesis testing involving a symmetric H_A such as the one above would use a 2-sided test. For a 1-sided test: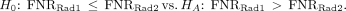A trial with this H_A hypothesizes that radiotracer 1 has a higher FNR, and worse performance, than radiotracer 2 in the target population. Whether the test is 1- or 2-sided is dependent on the question of interest, such as a primary or secondary objective, and is determined a priori.

Hypothesis testing is usually performed using a test statistic, which summarizes the sample information. Under a certain set of assumptions, a test statistic follows an exact or approximate distribution under H₀ that reflects the randomness associated with the sample. The P value, the probability of obtaining a statistic at least as extreme as the test statistic in the direction of H_A if H₀ were true, is used to interpret that test statistic (4). The smaller the P value, the stronger the evidence against H₀, leading one to reject it. Typically, this result is stated as being statistically significant in favor of H_A. Conversely, large P values do not provide enough evidence against H₀, leading one to fail to reject it. Not being able to reject H₀ does not make it true but rather allows one to conclude that there is not enough evidence to reject it.

Consider the 2-sided test statistic for comparing the FNR between 2 radiotracers for SLNB in NRG-HN006. Previous studies have suggested that the FNR of the SLNB procedure can be around 5%–15% (5). The value of the test statistic z for comparing the FNR between radiotracers 1 (15%) and 2 (7%) observed with 154 patients per group, assuming a normal approximation, is 2.26 (Table 2) (5). z is used to determine the P value by matching this value to probabilities of the standard normal distribution. With a 2-sided test, the P value corresponding to a z of 2.26 is 0.0238. The threshold, set a priori, to determine whether the P value is small enough to reject H₀ or large enough to fail to reject H₀ is known as the significance level. If the significance level is 0.05, which is commonly used, then there is enough evidence to conclude that the FNR differs between the 2 radiotracers since a P value of 0.0238 is less than 0.05 (i.e., H₀ is rejected). Statistical significance, however, does not provide evidence on the magnitude of the effect, making a statistically significant difference not necessarily clinically meaningful. For example, in a large sample size, a small effect can reach statistical significance because of the small variation in the sample. Likewise, if the sample is too small, large effects may fail to be deemed statistically significant because of the large amount of chance variation (i.e., the analysis is underpowered).

The significance level also represents the probability of type I error, denoted as α. This error occurs when H₀ is rejected but is actually true (Table 3). Thus, there is the truth for the population and a decision to be made using the sample, yielding 4 possible scenarios. In addition to the type I error, the type II error is an incorrect decision that occurs when H₀ fails to be rejected but is actually false (i.e., H_A holds); its probability is denoted as β. The 2 correct decisions are rejecting H₀ when it is false and failing to reject H₀ when it is correct.

Statistical power is related to the type II error by being its complement, 1 − β. Thus, the statistical power of a hypothesis test is its ability to identify a specified effect size at α significance level or, conversely, to reject H₀ when H_A is true—a correct decision described above. Ideally, a trial should have enough power to correctly conclude H_A when it is true. With continuous outcomes, 4 main components impact power: the specified effect size, the significance level, the sample size n, and the population variance σ². Specifically, power increases with larger effect sizes, higher values of α, larger sample sizes, and less variability within the sample. Most clinical trials are designed with statistical power ranging from 80% to 95%. Trials with power of less than 80% or an overly optimistic hypothesized treatment effect size are usually considered underpowered (6).

CIs are used to determine the range of possible values of the true parameter, determined from the sample data, based on a certain level of confidence. For instance, 95% CIs are commonly used and indicate that with 95% confidence, the true value being estimated is within the interval. The level of confidence is determined by 1 − α and, in general, is thus equivalent to the probability of failing to reject H₀ when H₀ is true. In many cases, since the level of confidence is determined on the basis of the significance level, α, interpretation of the CI will correspond to that of the statistical test. For instance, if the FNR estimate for radiotracers 1 and 2 based on 154 patients per group is 15% and 7%, respectively, the 95% CI based on a normal approximation of the difference in FNR between the 2 radiotracers is 1.1%–14.9% (Table 2). The CI for the difference in FNR between the radiotracers does not contain 0, which would allow one to conclude that the radiotracers perform differently in terms of FNR. This result corresponds to the P value for the test in the prior example—a P value of 0.0238, which is less than an α of 0.05—which produces a statistically significant result.

PARAMETRIC VERSUS NONPARAMETRIC TESTS

When the assumption that the sample data follow a known probability distribution is met, such as the normal distribution, parametric tests can be used. The t test, which is used to test the difference between 2 means, is a parametric test that assumes the sample data come from a normally distributed population (7). In large samples (e.g., >30) that do not meet the normality assumption, methods based on the normal distribution can still be used after invoking the central limit theorem. Broadly speaking, the central limit theorem states that regardless of the distribution of the population, as the sample gets larger, the distribution of the sample means approaches a normal distribution (8). This allows tests that assume data are normally distributed to be used to compare means. Versions of the t test can be used in 2 independent samples or in paired samples (i.e., pretest and posttest samples). An ANOVA is an extension of the t test to more than 2 independent samples.

In small samples or those that draw from populations with heavily skewed distributions, nonparametric tests can be used instead. The distribution of the nonparametric test statistic can be derived under H₀ without specifying the underlying distribution of the population (8). The Wilcoxon–Mann–Whitney test is the nonparametric version of the 2-independent-sample t test, whereas the Wilcoxon signed-rank test is the counterpart to the paired t test (Table 4) (9,10). The Kruskal–Wallis test can be used to test differences between more than 2 independent groups. Nonparametric tests are not testing means, as in a t test, but rather assign ranks to the data in order to test for differences in the groups’ probability distributions; thus, nonparametric tests typically report medians.

The χ² goodness-of-fit test was used when comparing FNR, a proportion, between 2 independent groups. χ² tests can be used for a single proportion, such as comparing the FNR of a diagnostic test with a fixed value, or for 2 independent groups, as previously presented. The χ² test is a nonparametric test (since it does not require that the sample data follow a distribution) that uses frequencies from categoric or count data to describe how well these data fit with H₀. The expected value of 80% of the counts is required to be at least 5 for the test to have a good approximation to the χ² distribution (11). If this assumption is violated, other tests, such as the Fisher exact test, can be considered. The exact binomial test, a parametric test based on the binomial distribution, can be used for binary data for a single proportion.

MULTIPLICITY

Recall that the type I error, α, is the probability of incorrectly rejecting H₀. In a single study with an α of 0.05, a type I error is expected to occur 5% of the time. Take the context of brain imaging, with tests performed on each vertex of the image representation of the brain, as an example (12,13). Roughly 100,000 voxels are obtained from a series of 3-dimensional brain volumes with the same number of hypothesis tests to depict activated regions (13). If α is 0.05, then 5,000 false-positive results would be expected. Control of the familywise error rate, the probability of at least one type I error in the trial, is thus desired under the presence of multiple testing (14).

Multiple methods exist to control the type I error rate. The Bonferroni adjustment may be the most commonly used but is also the most conservative, which can be desirable if strict control of the type I error is desired (15). When there are coprimary endpoints in a study, such as in NRG-HN006, a Bonferroni adjustment would require splitting the type I error. To maintain an overall α of 0.05, each endpoint may use an α of 0.025. This increases the sample size required.

A study can be designed to avoid the issue of multiplicity. Hierarchic testing is a method to control the type I error rate without affecting a clinical trial’s sample size (16). In NRG-HN006, the coprimary endpoint of disease-free survival is assessed first, and if noninferiority is shown, quality-of-life superiority is tested. This allows both tests to use an α of 0.05 while maintaining an overall α of 0.05.

Alternatively, control of the false-discovery rate, which is the proportion of significant results that are actually false-positives, can be used to correct for multiplicity (17). False-discovery rate–based methods are often preferred at early stages of discovery because of their higher power to detect true-positives while controlling the proportion of type I errors. A less conservative approach than the Bonferroni adjustment that is commonly used in function MRI analysis is the Hochberg step-down procedure, which adjusts for multiplicity by controlling the false-discovery rate (13,17,18). This procedure orders the P values beginning with the least significant and compares each with an adjusted type I error, a′. Once the P value is less than a′, the comparisons stop and that test and all following tests are deemed statistically significant. Details on and comparisons of the corrections addressed here, as well as additional ones, such as parametric tests, can be found elsewhere (12–14,19).

DIAGNOSTIC TESTING

In biomedical studies, diagnostic tests or procedures are typically used to determine the presence or absence of a disease or health condition. Diagnostic tests can be used for screening or surveillance, treatment monitoring, or staging. Some examples of diagnostic imaging tests are radiography, PET, CT, PET/CT, MRI, and ultrasound (20). Test-accuracy studies are usually designed to answer diagnostic or prognostic questions. Diagnostic test-accuracy studies use the test information to classify a patient into a current health status, whereas prognostic test-accuracy studies refer to the risk of a future health status. An example of a prognostic test-accuracy study is given by the NRG-HN002 substudy that estimated the accuracy of 12- to 14-wk posttherapy ¹⁸F-FDG PET/CT results to predict 2-y locoregional control (21). In general, a diagnostic test under study is also known as the index test (22). The true disease state is determined using a gold standard or reference standard test. In test-accuracy studies with a diagnostic goal, index tests are usually proposed because they are associated with lower costs and faster results or are less invasive. For instance, serology tests to detect the presence of antibodies in the blood when the body is responding to severe acute respiratory syndrome coronavirus 2 are considered index tests. These tests show whether a person has been infected by coronavirus in the past. Antigen tests can also be considered index tests, but they instead diagnose active coronavirus infections. Because antigen tests have a higher chance of missing an active infection, negative test results are usually confirmed with a molecular test. Because of their high diagnostic accuracy, molecular tests such as the nucleic acid amplification test are considered the gold standard to determine whether a patient has coronavirus disease 2019. Several antigen and antibody tests have been proposed because of their lower costs and sometimes faster results. In the NRG-HN002 prognostic test-accuracy substudy, the ¹⁸F-FDG PET/CT at 12–14 wk after treatment is the index test, and the protocol-specified method to assess locoregional failure at 2 y after randomization is the reference standard (21).

Continuing with the NRG-HN006 example of radiotracers, the SLNB with a given radiotracer is the index test, which was used to determine lymph node metastasis. The SLNB result is a positive or negative nodal metastasis according to the pathology findings from the SLNB. The subsequent development of isolated cervical metastasis assessed through standard imaging after the SLNB is the reference standard. A patient is called a false-negative if there is a lymph node metastases but the SLNB gives a negative result (Table 5). Conversely, a patient is called a false-positive if there is no lymph node metastases but the SLNB predicts a positive result. The FNR, a measure to assess the performance of a diagnostic test, determines the proportion of incorrect negative test results among individuals with the disease. The sensitivity (1 − FNR, or the true-positive rate) of the test indicates the probability of a positive result among those with the disease (Table 6) (23). Similarly, the false-positive rate (FPR) determines the proportion of incorrect positive test results among those without the disease. The specificity of the test (1 − FPR, or the true-negative rate) indicates the probability of a negative result among those individuals without the disease. The ideal diagnostic test should have high specificity and sensitivity (24). A trade-off between specificity and sensitivity depends on whether the diagnostic test is used for screening, staging, or prognosis.

In SLNB, an objective can be to estimate the ability of the SLNB to predict an N0 neck result (i.e., no lymph node metastasis) since these patients may avoid an unnecessary neck dissection. That is, what is the probability of developing isolated cervical metastasis after a negative SLNB (i.e., N0 neck)? The negative predictive value (NPV) of a test indicates the probability of not having the disease given a negative test result. Likewise, the positive predictive value (PPV) represents the probability of having the disease given a positive test result. The complements of the NPV and PPV are called the false-omission rate and false-discovery rate, respectively. Although the sensitivity and specificity are quantities inherent in the performance of the diagnostic test, the NPV and PPV depend not only on the test’s performance but also on the prevalence of the disease or health condition (Fig. 1).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 1.

Relationship between NPV, specificity, and disease prevalence when sensitivity of diagnostic test is 50% and 90%. D⁻ and D⁺ = number of patients without and with true nodal metastasis, respectively; P = prevalence; T⁻ and T⁺ = number of patients with negative and positive SLNB results, respectively.

In the Sentinel European Node Trial, patients with a negative SLNB who subsequently developed cervical metastasis and had a negative primary tumor site were classified as false-negatives (25). It is typical in SLNB studies that the number of false-positives is deliberately kept to zero since a positive SLNB result is deemed sufficient to declare the presence of cervical nodal metastases (Table 7) (26). That is, the specificity and PPV of the SLNB are both 100% (FPR is 0%). Occult lymph node metastases not detected by the SLNB (false-negatives) are of concern to clinicians since these patients may receive alternative therapies, such as close observation for low-risk patients (2). Patients with occult nodal metastasis may be at risk of distant metastatic disease given that the cancer has spread to the lymph node basins. However, if the SLNB predicts N0 necks with high probability, these patients may avoid unnecessary therapy and its implications relative to morbidity, decreased quality of life, and cost. False-negatives in SLNB can occur if the lymphatic pathway to the involved node is blocked, if the pathologist fails to detect micrometastasis or isolated tumor cells inside a lymph node, or if the surgeon misses a positive sentinel lymph node because of poor training or the complexity of the surgical region (26). An estimate of the FNR for SLNB in oral cancer is 15 of 109 cases, or 0.138 (13.8%) (Table 7). Assuming normality, a 95% CI for the FNR is 0.073–0.203 which indicates that the true FNR is between 7.3% and 20.3% with 95% confidence. This FNR estimate for the SLNB is of concern to some clinicians since roughly 1 or 2 of 10 patients could be incorrectly diagnosed. The NPV for the SLNB to detect N0 neck patients is given by 306 of 321 cases, or 0.95. Similarly, the sensitivity and specificity of the SLNB are 0.86 (94/109) and 1.00 (306/306), respectively. For a given patient, the probability of having lymph node metastasis after a negative SLNB result increases to 0.95 from 0.74, the latter being the probability of no nodal metastasis before the SLNB. It is important to interpret the NPV (and PPV) after considering disease prevalence. For a given sensitivity and specificity rate, the NPV increases as the prevalence of the disease decreases (Fig. 1). Publications by Civantos et al. and Hines et al. provide additional examples of these terms (26,27).

An example of a prognostic test-accuracy study is a potential NRG-HN006 substudy assessing the predictive accuracy (NPV) of ¹⁸F-FDG PET/CT when combined with END or SLNB to predict 1-y locoregional control. Patients with negative results on ¹⁸F-FDG PET/CT and on END or SLNB (index test) would have locoregional control assessed at 1 y using standard imaging and a biopsy confirmation (reference test) per protocol-specified techniques. Only the row with the negative index test results from Table 5 is included in the study by design. Given the negative index results, the locoregional control rates at 1 y can be compared using a χ² test.

When designing a test-accuracy study, it is crucial to carefully examine the objectives and, therefore, the design type, as it dictates what accuracy measures can be properly estimated from the data. For instance, NPV and PPV cannot be estimated from a case-control design given that the proportion of patients with the disease based on the reference standard is manipulated by researchers, for example, by setting a 1:1 case-control matching (28). One of the NRG-HN006 eligibility criteria is an ¹⁸F-FDG PET/CT–negative result for lymph node metastasis. Thus, a reasonable inference target would be to estimate the NPV of ¹⁸F-FDG PET/CT in this population within only the END arm since the number of patients with a negative index test is fixed by researchers through the trial design. In this case, the true metastatic nodal status is determined by the pathologic findings after the END.

RECEIVER-OPERATING-CHARACTERISTIC (ROC) ANALYSIS

In many applications, investigators use continuous or ordinal biomarkers or build predictive models based on a continuous or ordinal scale using a combination of variables such as biomarkers, gene expression, and patient characteristics, among others (29). A single biomarker or predictive model can be regarded as a classifier for purposes of diagnostic testing. These classifiers can, however, be converted into a binary classifier after selection of a given threshold on a suitable scale. For instance, logistic regression models are usually used to construct classifiers based on a set of predictors (30). Often, thresholds are selected on a probability scale. For instance, if a patient has a predictive probability of more than 0.5 based on the logistic model, then that patient will be considered a positive result for diagnostic purposes. This binary classifier based on a threshold can then be framed within the binary diagnostic testing discussion presented in Table 5. The selection of a threshold should follow some type of optimality criterion to obtain a classifier (diagnostic test) with at least acceptable accuracy. The discriminative power or diagnostic performance of a classifier is usually summarized and measured using the area under the ROC curve (AUC) (31). The ROC curve plots the FPR (1 − specificity) by sensitivity for different thresholds (Fig. 2). A classifier that perfectly predicts the disease status among those with and without the disease has an AUC of 1. Randomly predicting the disease status leads to a classifier with an AUC of 0.5. The AUC can also be interpreted using probabilities. Assume a rater is asked to score 2 individuals, one with the disease and the other without. The AUC can be seen as the probability that the rater will give a higher score to the individual with the disease than to the patient without the disease. An alternative interpretation of the AUC is that it is the average sensitivity across all possible FPRs. A publication by Hyun et al. provides an example using AUC (32).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 2.

ROC curve. Each point along curve represents set of coordinates (1 − specificity, sensitivity) for classifier defined by threshold. Diagonal line represents random classifier. D⁻ and D⁺ = number of patients without and with true nodal metastasis, respectively; T⁻ and T⁺ = number of patients with negative and positive SLNB results, respectively.

The goal in an ROC analysis is, therefore, to select an optimum threshold that produces a classifier closer to the upper left corner of the graph. For a random classifier (i.e., classification of an individual within each disease status is done randomly with equal probability, using, for instance, a fair coin), the NPV is 1 − disease prevalence. This result tells us that the classifier does not improve the predictive ability of nondisease.

The AUC is a statistic allowing typical inferential procedures to be applied. Namely, it is possible to perform hypothesis testing and CI estimation for the AUC. Likewise, it is possible to compare the AUC for 2 or more groups.