Abstract
β-amyloid (Aβ) accumulation in the brain is 1 of 2 pathologic hallmarks of Alzheimer disease (AD), and the spatial distribution of Aβ has been studied extensively ex vivo. Methods: We applied mathematical modeling to Aβ in vivo PET imaging data to investigate competing theories of Aβ spread in AD. Results: Our results provided evidence that Aβ accumulation starts in all brain regions simultaneously and that its spatiotemporal distribution is due to heterogeneous regional carrying capacities (regional maximum possible concentration of Aβ) for the aggregated protein rather than to longer-term spreading from seed regions. Conclusion: The in vivo spatiotemporal distribution of Aβ in AD can be mathematically modeled using a logistic growth model in which the Aβ carrying capacity is heterogeneous across the brain but the exponential growth rate and time of half maximal Aβ concentration are constant.
The major constituent of neuritic plaques, which appear to play a key role in the pathogenesis of Alzheimer disease (AD) (1–3), is β-amyloid (Aβ) (4,5). The spatiotemporal distribution of Aβ in AD has been extensively characterized ex vivo through neuropathologic studies using Aβ immunostaining (6–8). A consistent spatiotemporal distribution is observed with Aβ, initially restricted to a small number of brain regions before becoming widespread later in the disease (6,8). There are competing hypotheses for the biologic mechanism causing the evolution of Aβ pathology. One hypothesis is that Aβ accumulation is determined by properties of the local tissue environment (9–12). A second hypothesis is that Aβ originates in a small number of seed regions and, over the duration of the disease, spreads to other brain regions by means such as prion-like self-propagation or transynaptic spread (7,13–16).
The in vivo regional Aβ concentration can be measured in humans using PET. Large-cohort cross-sectional studies have been performed (17,18), but analysis has focused mainly on classifying the distinct clinical phases of the disease. This approach has provided relatively little information about the way Aβ plaques accumulate over time. Analysis of longitudinal studies has been restricted to either short time windows of no more than 2 years (19–21) or the average deposition across the whole cortex (22). Thus, despite the large amount of in vivo data collected, the spatiotemporal distribution of Aβ has yet to be fully characterized.
The logistic growth model has been used to model the growth of a wide range of biologic and clinical phenomena, such as the postglacial expansion of forest trees (23), the in vitro pharmacodynamics of bactericidal kinetics (24), and, most interestingly, in vitro Aβ fibrillation (25). Here, we introduce the logistic growth model to provide a mathematical description of a sigmoidal increase in Aβ concentration over time (Fig. 1), Eq. 1where t is the time through the accumulation process (a t of 0 corresponds to a time point at which Aβ levels are minimal), SUVr(t) is the PET Aβ SUV ratio at time t, Aβ(t) is the concentration of Aβ at time t, NS is the tracer nonspecific binding, r is the exponential uninhibited growth rate, T50 is the time of half-maximal Aβ concentration, and K is the carrying capacity.
Eq. 1where t is the time through the accumulation process (a t of 0 corresponds to a time point at which Aβ levels are minimal), SUVr(t) is the PET Aβ SUV ratio at time t, Aβ(t) is the concentration of Aβ at time t, NS is the tracer nonspecific binding, r is the exponential uninhibited growth rate, T50 is the time of half-maximal Aβ concentration, and K is the carrying capacity.
Logistic growth model describing Aβ PET imaging signal over time as function of PET NS, K, T50, and r.
It is possible to test between the two competing hypotheses for Aβ accumulation by considering whether each of the 4 model parameters is constant across different brain regions or whether they are regionally different. A summary of the different logistic growth models is displayed in Figure 2. If T50 varies between regions, the model is consistent with longer-term spreading from seed regions because seed regions would have a lower T50 than other regions (models shown in gray in Fig. 2). If T50 is constant across the brain, the model is consistent with local tissue properties driving the accumulation process (models shown in white in Fig. 2). Application of statistical model selection criteria allows us to test between the competing hypotheses.
Sixteen logistic growth models of Aβ accumulation with example curves from 3 distinct brain regions. Models in gray have regionally different T50s and are consistent with spreading from seed regions, whereas models in white are consistent with local tissue properties driving Aβ accumulation process.
We took a novel approach to testing between the competing models of Aβ accumulation: we used the whole-cortex Aβ profile derived from the longitudinal study of Jack et al. (in which the patients did not receive any treatment) (26) to transform a large cross-sectional study into a chronological dataset by assigning each subject in the cross-sectional dataset a time through the accumulation process. This dataset enabled full spatiotemporal modeling of the Aβ accumulation process in AD, at a population level. Applying the logistic growth model to in vivo Aβ accumulation in this dataset allowed us to test whether accumulation was best explained by the longer-term spreading of amyloid from seed regions or by heterogeneous regional carrying capacities across brain regions.
MATERIALS AND METHODS
Longitudinal Model of Aβ Accumulation
We introduce a logistic growth model to describe the accumulation of Aβ in the human brain. The model assumes that the rate of change of Aβ concentration is proportional to the product of the current concentration of Aβ and a term limiting growth due to the K of the local environment. The model is defined by the following differential equation: Eq. 2
Eq. 2
Solving the differential equation yields a function for the concentration of Aβ over time: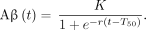 Eq. 3
Eq. 3
In vivo PET amyloid tracers are quantified in terms of the SUVr between a target region containing amyloid and a reference region containing only background NS, and therefore: Eq. 4
Eq. 4
Substituting Equation 3 for Aβ(t) into equation 4 yields the bottom line of Equation 1, which describes the temporal evolution of the in vivo PET Aβ signal over time (with the 4 parameters NS, r, T50, and K).
Imaging Data
A chronological Aβ dataset for the AD disease pathway at the population level was generated by transforming a large cross-sectional Aβ dataset using a population time course for the mean cortical SUVr obtained in a smaller longitudinal study.
Cross-sectional 18F-AV-45 ((E)-4-(2-(6-(2-(2-(2-18F-fluoroethoxy)ethoxy)ethoxy)pyridin-3-yl)vinyl)-N-methyl benzeneamine) human Aβ PET imaging data and structural MRI data were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (27) for 779 subjects. The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner. The primary goal of ADNI has been to test whether serial MRI, PET, testing of other biologic markers, and clinical and neuropsychologic assessment can be combined to measure the progression of mild cognitive impairment and early AD. Up-to-date information can be found online at www.adni-info.org.
18F-AV-45 Human Aβ PET Imaging Data
Each subject underwent a 20-min 18F-AV-45 PET scan 50 min after injection (370 ± 37 MBq) according to the standardized ADNI protocol (28). Three image preprocessing steps were applied to the data before entry into the ADNI imaging database (http://adni.loni.usc.edu/methods/pet-analysis/). Briefly, 4 late-time 5-min frames were coregistered and averaged. The resulting image was converted to a 160 × 160 × 96 voxel static image with voxel dimension of 1.5 × 1.5 × 1.5 mm. Finally, a gaussian filter of 8 mm in full width at half maximum (corresponding to the lowest-resolution scanner used in the study) was applied. These primary data were downloaded from the ADNI database and used in the subsequent analyses.
T1-Weighted MRI Data
All subjects underwent T1-weighted 1.5-T structural MRI; the MR images were downloaded from the ADNI imaging database.
Image Processing
Registration of Images into Stereotactic Space
18F-AV-45 data were nonlinearly registered into Montreal Neurological Institute 152 (MNI152) space (29) using DARTEL (30). Initially, the structural MR images were segmented into gray matter and white matter using SPM12 and registered to a group-average template. The group-average template was then registered to MNI152 space. Each subject’s 18F-AV-45 SUVr image was registered to the corresponding MR image using a rigid-body registration. Finally, the individual’s DARTEL flow field and template transformation were applied without modulation, resulting in 18F-AV-45 images in MNI152 space. The normalized maps were spatially smoothed (gaussian kernel of 8 mm in full width at half maximum). Each registration was visually assessed, with the data of 10 subjects being rejected. Therefore, the final dataset used to construct the chronological data contained 769 subjects.
Calculation of SUVr Data
A neuroanatomic atlas (31) containing 90 cortical and subcortical regions, and a gray matter probability atlas in MNI152 space, were used to calculate SUVr data. SUVr data were quantified using the gray matter cerebellum as the reference region, which was defined as the intersection between voxels that are in the cerebellum region of interest in the neuroantomic atlas and voxels that have an intensity of over 0.5 in the gray matter probability map. The mean uptake value for the gray matter cerebellum region of interest was obtained, and each image was divided by this mean value to generate an SUVr image for each subject. Finally, the 90 regions of interest were applied to this image to derive regional SUVr data for each subject. Finally, an average cortical SUVr was obtained by calculating the mean SUVr for all 76 cortical regions (weighted by region volume).
Construction of Population-Level Chronological Aβ Data
Jack et al. (26) presented a functional form describing the time course of mean cortical SUVr in AD by integrating rates of change of SUVr in a longitudinal study. Demographics for the study are summarized in Table 1.
Subject Characteristics
Conversion of Functional Form into 18F-AV-45 SUVr Units
The functional form (kindly provided to us by Clifford Jack (26)) was derived from longitudinal Aβ imaging data using 11C-Pittsburgh compound B rather than 18F-AV-45. Previous work scanning the same subjects with both 11C-Pittsburgh compound B and 18F-AV-45 showed that a linear equation can appropriately convert between the different PET tracers (32–34): AV-45 SUVr = a(Pittsburgh compound B SUVr) + b. Therefore, the 11C-Pittsburgh compound B–derived functional form was transformed into 18F-AV-45 SUVr units so that the resultant function  ranged between the mean of the 2.5th and 97.5th cortical 18F-AV-45 SUVr percentiles for the cross-sectional ADNI dataset (a = 0.72 and b = 0.02).
ranged between the mean of the 2.5th and 97.5th cortical 18F-AV-45 SUVr percentiles for the cross-sectional ADNI dataset (a = 0.72 and b = 0.02).  describes the time course of 18F-AV-45 mean cortical SUVr in AD.
describes the time course of 18F-AV-45 mean cortical SUVr in AD.
Timepoint in Chronology of AD
We used  to determine a time in the chronology of AD, t, for each of the 769 subjects in the cross-sectional study by calculating their mean cortical SUVr and then finding the value for t from
to determine a time in the chronology of AD, t, for each of the 769 subjects in the cross-sectional study by calculating their mean cortical SUVr and then finding the value for t from  to which that SUVr corresponded in the range 0–30 y. This process generated a chronological dataset at the population level for the spatiotemporal accumulation of Aβ with data at 769 time points over the 30-y disease cascade.
to which that SUVr corresponded in the range 0–30 y. This process generated a chronological dataset at the population level for the spatiotemporal accumulation of Aβ with data at 769 time points over the 30-y disease cascade.
The calculated times were normally distributed, with a mean of 11.8 y and an SD of 5.12 y. It was verified that there was no relationship between the calculated t and SUV in the cerebellum. The test–retest variability of mean cortical 18F-AV-45 SUVr has been calculated to be less than 3% (35). This would translate to a variability of 0.68 y in calculated time through the disease process, for a median SUVr of 1.3.
The coherence of the regional curves in the cross-sectional dataset (Fig. 3) shows not only that there is a stereotypic temporal accumulation at a global level but also that—relative to this stereotypic temporal accumulation—each region has an accumulation curve that is consistent across subjects.
Model fitting of most parsimonious logistic growth model (model 11) to chronological 18F-AV-45 Aβ PET data in 9 regions. Model accurately describes data for regions of high (top row), medium (middle row), and low (bottom row) accumulation. A = anterior; D = dorsal; inf = inferior.
Regional Analysis of Aβ Accumulation
The logistic growth model of Aβ accumulation (Eq. 1) was then fitted to the chronological data. To determine whether each of the 4 model parameters was constant across the whole brain or varied by region, we investigated 16 different models corresponding to all the permutations of using either global (the parameter is constant across all brain regions) or local (the parameter varies by region) values for each of the 4 model parameters. The full set of models is summarized in Table 2 and contains between 4 and 360 parameters.
Sixteen Parameterizations of Logistic Growth Model of Aβ Accumulation Used to Analyze Chronological 18F-AV-45 SUVr PET Data at Regional Level
Each model was fitted using a nonlinear trust-region reflective algorithm implemented in MATLAB (The MathWorks Inc.) that minimized the residual sum of squared errors subject to an Aβ(0) of less than 0.1 (this constraint did not occur for the optimum model). The Bayesian information criterion (BIC) (36) was used to select the most parsimonious model, and the posterior probability that each model was optimum was ascertained from the weights of each model (37–40).
Parametric Image Analysis of Aβ Accumulation
Having identified model 11 (global r and T50; local NS and K) as optimal on the basis of the regional analysis, we fitted this model at the voxel level to generate parametric images for NS and K. Parameter values for r and T50 were fixed from the regional analyses, and the individual voxel time course was fitted using a linearization of the model (supplemental material, available at http://jnm.snmjournals.org).
RESULTS
Chronological Aβ Dataset
A chronological Aβ 18F-AV-45 dataset was created in stereotactic space from 769 subjects who ranged from healthy individuals to AD patients. The chronological data exhibited coherent but different trajectories within individual regions, providing evidence of a stereotypic spatiotemporal distribution at the population level (Fig. 3).
Model Selection and Implications
Each of the logistic growth models was fitted to the chronological in vivo PET data at a regional level to investigate the spatiotemporal evolution of the Aβ signal in the AD process. The 16 logistic growth models were successfully fitted, and model 11 was identified as the most parsimonious description of the data as determined by the BIC model selection criteria (Table 1). The difference in BIC between model 11 and all the other models was at least 267. Evidence is considered strong when the difference in BIC is greater than 10 (41). The posterior probability that model 11 is the best choice was also high (P > 0.999999). The model accurately describes the time course of Aβ accumulation in all regions (Supplemental Figs. 1 and 2). A selection of 9 regions with different levels of Aβ accumulation is displayed in Figure 3, demonstrating the ability of the model to accurately describe distinct regional time courses.
Model 11 requires that regional values for K and tracer NS vary. In contrast, T50 and r are constant across brain regions in this model. This suggests that regional variability in Aβ carrying capacities determines the distribution of Aβ concentration, because regions with higher carrying capacities will accumulate more amyloid over time. These results support the hypothesis that Aβ accumulation is limited by properties of the local tissue environment. The observation that the data are best explained by a model with a global T50 provides evidence against the spreading hypothesis, as long-term spreading from seed regions would imply a shorter T50 for seed regions and therefore require a model (such as model 12) with a local T50.
The analysis process was also run on 2 additional sets of regions of interest: a set of 9 regions of interest that are larger and cover the whole brain, and a parcellation that is restricted to cortical regions. Model 11 was the optimum model for both these alternative analyses (Supplemental Tables 2 and 3).
For model 11, the carrying capacity was highest in the anterior cingulate gyrus, precuneus, and frontal operculum cortex (1.55, 1.50, and 1.46 SUVr units, respectively), intermediate in parts of the frontal cortex and insular cortex (1.13 and 1.19), and low in the thalamus and brain stem (0.48 and 0.38). The global T50 was 14.9 y, and the global r was 0.20 y−1.
Parametric Imaging of K
The regional variation normally seen in AD was predicted when model 11 was fitted at the voxel level using the fixed global values of r (0.20 y−1) and T50 (14.9 y) estimated from the regional analysis. Parametric images were generated for K and NS (Fig. 4).
Parametric images displayed as orthographic projections for K and NS obtained from fitting model 11 at voxel level. Gray matter (GM) and white matter (WM) probability maps are displayed for reference. Highest carrying capacities were in frontal lobe, and lowest were in cerebellum, occipital lobe, and brain stem. NS image is consistent with known NS of 18F-AV-45 to white matter.
DISCUSSION
Using a logistic growth model, we have mathematically modeled with a high degree of accuracy the spatiotemporal distribution of amyloid in the brain as AD pathology increases. Our results support the hypothesis that regional accumulation of Aβ originates at the same time, and has the same r, in all regions. The implication is that the heterogeneous Aβ distribution observed in AD is caused by a property of the local tissue environment rather than by longer-term spreading from seed regions, as the latter would require different values of r or T50 (e.g., for long-term spreading, T50 would be expected to be earlier in seed regions). If the T50 differed in different regions, it would have been impossible to distinguish whether the onset of accumulation occurs at different times in different regions or whether the rate of accumulation differs in different regions. Both mechanisms would require a heterogeneous T50 across regions. Because this heterogeneity was not found, one can infer that accumulation begins at the same time and occurs at the same rate in all regions.
Our analysis shows that the spatiotemporal distribution of Aβ at the population level can be accurately modeled using a 4-parameter logistic growth model, where K and NS vary across the brain but r and T50 are constant. A model with these characteristics was clearly identified as the most parsimonious model using the BIC model selection criteria. Interestingly, this model has previously been shown to be capable of characterizing the accumulation of Aβ in vitro (25).
The current work had some limitations. First, to model the accumulation of Aβ in AD at the population level, we assumed that there is a consistent spatiotemporal distribution for all subjects within the cross-sectional ADNI cohort, which may be an oversimplification. However, the clear coherence of individual trajectories in all brain regions (Supplemental Figs. 1 and 2) and previous postmortem data (6) provide confidence that this assumption is reasonable. Second, when creating the cross-sectional dataset, we assumed that all subjects in the longitudinal data and in the cross-sectional study were following the same accumulation trajectory. Table 1 shows demographics for both studies. Both studies have scans from healthy controls, patients with mild cognitive impairment and AD patients, and the subjects are well matched on all characteristics apart from the number of cognitively impaired subjects, which was lower in the longitudinal study. Third, the outcome measure that we have considered (SUVr) does not account for brain atrophy during the 30-y period and the impact that this factor may have on Aβ signal. Studies have shown that the rate of atrophy is greatest in medial temporal regions: 0.6%/y (SD, 0.7) for healthy controls, increasing to 1.5%/y (SD, 0.7) in AD patients (42). With these atrophy rates, it is unlikely that atrophy would have a significant impact on the model identification and conclusions presented. Further, it has been shown that atrophy occurs after Aβ accumulates in AD (43); therefore, atrophy is not likely to affect our result in this analysis. In the future, it will be important to further investigate the temporal relationship between regional Aβ accumulation and atrophy.
Spatiotemporal modeling of longitudinal data with the logistic growth model introduced here could have much wider utility. The trajectory of Aβ accumulation in dementias and neurodegenerative diseases with different patterns of Aβ needs to be investigated to ascertain whether the temporal process is the same but the topography driven by different regional carrying capacities or whether the accumulation process is actually different.
CONCLUSION
The in vivo spatiotemporal distribution of Aβ in AD can be mathematically modeled using a logistic growth model in which the Aβ K is heterogeneous across the brain but r and T50 are constant. This finding suggests that the heterogeneous Aβ accumulation in AD results from different regional carrying capacities rather than from longer-term spreading from a small number of seed regions.
DISCLOSURE
Data collection and sharing for this project were funded by the ADNI (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging and the National Institute of Biomedical Imaging and Bioengineering, as well as through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd. and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC; Johnson & Johnson Pharmaceutical Research & Development LLC; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education. Roger Gunn is a consultant for Abbvie and Cerveau. No other potential conflict of interest relevant to this article was reported.
Acknowledgments
Data used in preparation of this article were obtained from the ADNI database (adni.loni.usc.edu). As such, the investigators within the ADNI contributed to the design and implementation of ADNI or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at https://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf. The study was coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California. We thank Clifford Jack for kindly providing us with the longitudinal mean cortical PET SUVr data; Ilan Rabiner and Paul Matthews for helpful comments on the manuscript; and Yasser Ituria and Alan Evans for interesting discussions on this topic.
Footnotes
Published online Nov. 16, 2017.
- © 2018 by the Society of Nuclear Medicine and Molecular Imaging.
REFERENCES
- Received for publication April 11, 2017.
- Accepted for publication October 5, 2017.











