Abstract
64Cu emits positrons as well as β− particles and Auger and internal conversion electrons useful for radiotherapy. Our objective was to model the cellular dosimetry of 64Cu under different geometries commonly used to study the cytotoxic effects of 64Cu. Methods: Monte Carlo N-Particle (MCNP) was used to simulate the transport of all particles emitted by 64Cu from the cell surface (CS), cytoplasm (Cy), or nucleus (N) of a single cell; monolayer in a well (radius = 0.32–1.74 cm); or a sphere (radius = 50–6,000 μm) of cells to calculate S values. The radius of the cell and N ranged from 5 to 12 μm and 2 to 11 μm, respectively. S values were obtained by MIRDcell for comparison. MCF7/HER2-18 cells were exposed in vitro to 64Cu-labeled trastuzumab. The subcellular distribution of 64Cu was measured by cell fractionation. The surviving fraction was determined in a clonogenic assay. Results: The relative differences of MCNP versus MIRDcell self-dose S values (Sself) for 64Cu ranged from −0.2% to 3.6% for N to N (SN←N), 2.3% to 8.6% for Cy to N (SN←Cy), and −12.0% to 7.3% for CS to N (SN←CS). The relative differences of MCNP versus MIRDcell cross-dose S values were 25.8%–30.6% for a monolayer and 30%–34% for a sphere, respectively. The ratios of SN←N versus SN←Cy and SN←Cy versus SN←CS decreased with increasing ratio of the N of the cell versus radius of the cell and the size of the monolayer or sphere. The surviving fraction of MCF7/HER2-18 cells treated with 64Cu-labeled trastuzumab (0.016–0.368 MBq/μg, 67 nM) for 18 h versus the absorbed dose followed a linear survival curve with α = 0.51 ± 0.05 Gy−1 and R2 = 0.8838. This is significantly different from the linear quadratic survival curve of MCF7/HER2-18 cells exposed to γ-rays. Conclusion: MCNP- and MIRDcell-calculated S values agreed well. 64Cu in the N increases the dose to the N in isolated single cells but has less effect in a cell monolayer or small cluster of cells simulating a micrometastasis, and little effect in a sphere analogous to a tumor xenograft compared with 64Cu in the Cy or on the CS. The dose deposited by 64Cu is less effective for cell killing than γ-rays.
Because it can be routinely produced in a biomedical cyclotron and emits moderate energy positrons (Emax = 0.653 MeV [19%]) that provide good spatial resolution (0.7 mm), 64Cu is an attractive radionuclide for positron-emission tomography. The half-life of 64Cu (12.7 h) is also compatible with the pharmacokinetics of peptides (1) or antibody fragments (2,3) that recognize tumor-associated receptors overexpressed on cancer cells. Moreover, many different bifunctional chelators that strongly complex 64Cu have been developed for conjugation to these targeting ligands (4). In addition to its positron emission, 64Cu emits β− particles, Auger and internal conversion (IC) electrons, and γ-photons. The β− particles and Auger electrons of 64Cu have been studied for radiation treatment of tumors (5–9). The maximum β− energy of 64Cu is 0.579 MeV (40%) (10). These particles have a maximum range in tissues of about 2 mm and are most suitable for treatment of small tumors (11). The Auger and IC electrons that are emitted during the electron capture (40%) decay of 64Cu have low energy (∼2 keV) and only a subcellular range of less than 1 μm (12). These forms of radiation are most suitable for killing single cells or small clusters of cells (e.g., micrometastases). In theory, the positron emissions of 64Cu may also be used to treat tumors, because the positron-emitting agent 18F-FDG has been shown to have tumor growth–inhibitory effects (13). The nucleus (N) of tumor cells is considered to be the critical target for radiation treatment. Because the Auger and IC electrons have a subcellular range, it is important to understand the effects of subcellular distribution of 64Cu on the radiation dose deposited in the N. The dose deposited by the β− and β+ emissions is also important, but because of their longer range, these emissions have a major cross-dose effect that can deposit dose in the N of a cell from radioactivity that is located outside the cell (e.g., in another cell or in the extracellular environment) within the 2-mm range of these particles. Various experimental geometries are used to assess the cytotoxic effects of radionuclides on tumor cells. These include single cell or monolayer geometries used in vitro (e.g., clonogenic assays), as well as small sphere geometries used in vivo in tumor xenograft mouse models. To appreciate the effects of these different geometries on the self-dose (the absorbed dose to the N from the radioactivity in the same cell) and cross-dose (the absorbed dose to the N from the radioactivity outside the cell) from 64Cu, we calculated the S values (the absorbed dose per unit time-integrated radioactivity) to the N from radioactivity located at the cell surface (CS) or in the cytoplasm (Cy) or N of a single cell, in a closely packed monolayer of cells in different-sized culture plates, or in a spheric cluster of cells with different dimensions. These S values were calculated by Monte Carlo N-Particle (MCNP) modeling (14) and were compared with the values from the MIRD publication (15) and calculated by MIRDcell software (16). Previously, we found that MCNP computer code was able to assess both the self-dose and the cross-dose to the N from the Auger electron emitter 111In with accuracy comparable to that by analytic methods (17). Finally, the survival fraction (SF) for human epidermal growth factor receptor-2 (HER2)–overexpressing MCF7/HER2-18 cells exposed in vitro to 64Cu-labeled trastuzumab was determined by clonogenic assay and plotted versus the absorbed dose calculated by the MIRD schema using MCNP-calculated S values and time-integrated activity determined by cell fractionation. The survival curve of MCF7/HER2-18 cells exposed to 64Cu-labeled trastuzumab was compared with that for γ-rays.
MATERIALS AND METHODS
Cell Culture and 64Cu-DOTA-Trastuzumab
The human breast cancer cell line MCF7/HER2-18, stably transfected with the HER2 gene and overexpressing HER2 (1.2 × 106 HER2/cell), was donated by Dr. Mien-Chiu Hung (MD Anderson Cancer Center, Houston) (18). These cells were cultured in Dulbecco's modified Eagle medium/Ham's F12 1:1MIX + antibiotics supplemented with 10% fetal bovine serum and geneticin (0.5 mg/mL; Gibco) at 37°C and 5% CO2. Trastuzumab (Herceptin; Hoffmann-La Roche) was derivatized with 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid mono N-hydroxysuccinimide ester (DOTA-NHS; Macrocyclics) as previously reported (2). Details are provided in the supplemental materials (available at http://jnm.snmjournals.org).
Clonogenic Assays and Cell Fractionation Studies
MCF7/HER2-18 cells (7 × 105 cells/well) cultured to subconfluence overnight in 6-well plates were incubated with 1.9 mL of 64Cu-DOTA-trastuzumab (0–0.368 MBq/μg, 67 nM) for 18 h, then clonogenic assays were performed as previously reported (19). The details are provided in the supplemental materials. The SF versus the MCNP-calculated absorbed dose to the N was plotted and fit to a linear or a linear-quadratic survival curve, then compared with the survival curve of MCF7/HER2-18 cells exposed to γ-rays, which we previously found to follow a linear-quadratic model (Eq. 1):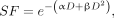 Eq. 1
Eq. 1
where α and β were 0.823 and 0.02633 Gy−2, respectively (19).
For subcellular uptake experiments, subconfluent MCF7/HER2-18 cells (7 × 105 cells/well) cultured overnight in 6-well plates were incubated with 64Cu-DOTA-trastuzumab (0.245 MBq/μg, 67 nM) in 1.9 mL of medium for 1, 3, 15, or 18 h. For subcellular efflux experiments, subconfluent MCF7/HER2-18 cells (1.3 × 107 cells) cultured overnight in a 175 cm2 flask were incubated with 64Cu-DOTA-trastuzumab (0.245 MBq/μg, 67 nM) in 25 mL of medium for 18 h and harvested by trypsinization, then 5 × 105 cells/well were seeded and cultured in 6-well plates with 3 mL of medium per well for 9.5, 22.5, 30, and 50 h. At the end of incubation, cell fractionation was performed as previously reported to isolate the CS, Cy, or N radioactivity, which was measured in a γ-counter (20). Details are provided in the supplemental materials. This method provides complete separation of trastuzumab in the Cy from the N (<1%), which we validated for MCF7/HER2-18 cells by exposing similarly to Alexa-488–labeled trastuzumab (10 μg/mL) and visualizing the isolated nuclei by confocal fluorescence microscopy (Supplemental Fig. 1). We previously showed that this cell fractionation method yields nuclei without cytoplasmic contamination (20).
Calculation of S Values by Monte Carlo Simulation
MCNP Monte Carlo code (version 5; Los Alamos National Laboratory) (14) was used to estimate S values for dose deposition to the N from 64Cu for a single cell, a closely packed monolayer or cluster of cells of various dimensions. The positron and β− particle emission spectra of 64Cu were taken from Lund Nuclear Data (http://nucleardata.nuclear.lu.se) whereas the spectra of the Auger and IC electrons, x-rays, and γ-photons were based on the MIRD radionuclide data (10). The positron, β− particles, Auger and IC electrons, x-rays, and γ-photons, including the two 511-keV γ-photons from positron annihilation, were included in the MCNP input file to be directly sampled during the radiation transport simulation. The schematic cell geometry and modeling of 64Cu distributions used in MCNP simulation were similar to our previous publication on cellular dosimetry of 111In (17) and are shown in Figure 1. 64Cu was assumed to be distributed homogeneously at the CS, in the Cy or in the N, or in 0.2-cm-thick water in a tissue culture plate (non–cell-bound 64Cu). The cell and N were assumed to be concentric spheres, which fit tightly in a closely packed hexahedral universe in the case of the monolayer and cluster of cell geometries to facilitate the comparison of the S values calculated by MCNP with MIRDcell (16). For the purposes of the calculation, the radius of the cell and N (RC and RN) ranged from 5 to 12 μm and 2 to 11 μm, respectively. For simulating the exposure of cells seeded into wells in a 6-, 12-, 24-, 48-, or 96-well plate, the studied volume was defined as a cylinder with a radius of 1.74, 1.10, 0.77, 0.55, or 0.32 cm that contained 0.2-cm-thick water and had a 0.1-cm-thick polystyrene bottom on which a monolayer of cells, which were defined as breast tissue–equivalent phantom (ICRU-44) (21), was attached. To compare the MCNP results with those estimated by MIRDcell (16), the radius of the cylinder was set as 0.1 mm. For simulating the cluster of cells, the studied volume was defined as a sphere of breast tissue–equivalent phantom (21). The effect of the sphere radius (50, 100, 250, 500, 1,500, and 6,000 μm) on the S values was examined. Three types (maximum, minimum, and mean) of cross-dose S values (Scross) were calculated. To simplify the calculation, with the assumption that the energy deposited to target i from source j would be equivalent to the energy deposited to target j from source i if their shape, size, and relative position were kept the same, we applied a target-source reverse approach in the calculation of the maximum and minimum Scross values. For the maximum Scross, the cell from which the source particles were emitted was set at the center of either the well or the sphere. For the minimum Scross, the cell from which the source particles were emitted was set at the edge of either the well or the sphere farthest from the center. For the mean Scross, the source particles were emitted homogeneously from either a cylinder or a sphere. The energy deposition per starting particle in all cell nuclei of the monolayer or sphere in the case of maximum or minimum S values or in the cylinder or sphere in the case of mean S values was tallied. All emitted electrons with energy less than 1 keV were assumed to deposit all their energy locally within the same cell compartment in which 64Cu was located. The maximum or minimum absorbed dose to the N per starting particle was calculated by dividing the deposited energy by the mass of the N. The mean S values to either the cylinder or the sphere were calculated by dividing the deposited energy by the mass of the modeled breast tissue packed in the cylinder or sphere. The mean S values per cell were obtained by multiplying the mean S values per cylinder or sphere by cell numbers per cylinder or sphere. For each simulation, 1 × 104 to 1 × 106 particles were launched to reach an SD of less than 1% for all energy deposition results. The Scross values were determined by subtracting the respective self-dose S values (Sself) from the total mean S values. The Sself values to be subtracted from the total mean S values were calculated assuming the homogeneous distribution of 64Cu in a cube with the side equal to the diameter of the respective cell.
Schematic cell geometry used in MCNP simulation. (A) Top view of concentric spheres representing cell nuclei and cells, which fit tightly in a closely packed hexahedral universe in a 3-dimensional cluster or a monolayer. (B) Side view of monolayer cells in cell culture plate. RC = cell radius; RN = nucleus radius.
Calculation of S Values by MIRDcell
MIRDcell (version 2.0 software; http://mirdcell.njms.rutgers.edu/) (16) was used to calculate mean S values for dose deposition to the N from 64Cu for a closely packed monolayer of cells within a 0.2-mm-diameter circle or for a 0.5-mm-diameter spheric cluster of cells. The diameter of the cell and N ranged from 10 to 24 μm and 4 to 22 μm, respectively. The predefined MIRD radionuclide 64Cu and the full β-energy spectrum were chosen in the Radiation Source Table in the Source/Target tab; the N was selected as the target region; and the CS, Cy, and N were chosen as the source regions. In the Multicelluar Geometry tab, 2D Colony or 3D Cluster were selected. The distance between the cells, the percentage of cell binding, and the distribution of radioactivity among the cells were set at the cell diameter, 100%, and uniform, respectively. The maximum mean activity per cell (all cells) and time-integrated activity coefficient were set as default of 0.001 Bq and 100 h. At the completion of compute, the self-dose SN←N, SN←Cy, and SN←CS were shown in the right window of the output tab, and mean activity per cell (Bq) and the corresponding mean absorbed dose to the cell (Gy) were listed on the left window of the output tab. The mean S value was obtained by dividing the mean absorbed dose to the cell by mean activity per cell and time-integrated activity coefficient 100 h × 3,600 s/h. The Scross value was calculated by subtracting the Sself value from the corresponding mean S value.
Calculation of Mean Radiation Absorbed Dose to N
The mean radiation absorbed dose to the N was calculated on the basis of the MIRD schema (Eq. 2): Eq. 2
Eq. 2
where, Ã was the time-integrated activity in each source region (M = medium, CS, Cy, or N), and S was the MCNP-calculated mean S value for the medium or the respective cell compartments. When cells were incubated with 64Cu-DOTA-trastuzumab in a 6-well plate for 18 h, the mean S values were taken from the circular monolayer model with a 1.74-cm radius packed with 7 × 105 cells (RC = 10, RN = 8 μm). The time-integrated activity up to 18 h in the N, Cy, and CS compartments was calculated from the area under the curve for the radioactivity versus incubation time, measured in cell fractionation studies. The time-integrated activity up to 18 h in the surrounding medium was calculated on the basis of the physical decay of 64Cu using formula A0/λ × [1-exp(-λTD)], where A0 is the initial radioactivity in the medium, λ is the decay constant (1.52 × 10−5 s−1) for 64Cu, and TD is the dose-integration period. Once single cells were seeded in fresh medium and cultured for 10 d to allow colony formation, the S values were taken from the single cell model. The time-integrated activity in each cell compartment up to 50 h was calculated on the basis of efflux cell fractionation experiments, after which the radioactivity was under the detection limit and thus the time-integrated activity from 50 h to 10 d was assumed to be zero.
RESULTS
Comparison of MCNP- and MIRDcell-Calculated S Values
To evaluate the differences in subcellular S values calculated by MCNP simulation versus the MIRDcell-calculated values or MIRD-published values (15), the Sself and Scross values to the N for 64Cu uniformly distributed in the N, Cy, or CS compartments of a single cell or cubically close-packed cells of various dimensions in a 2-dimensional circular monolayer (radius = 0.1 mm) or 3-dimensional sphere (radius = 0.25 mm) were calculated by MCNP and MIRDcell (Supplemental Tables 1–3). The relative differences of MCNP-calculated versus MIRDcell-calculated Sself were −0.2 to −3.7% for SN←N, −8.5%–3.1% for SN←Cy, and −11.9%–10.5% for SN←CS, respectively. For a single cell with a constant cell radius, as the radius of the N increased, the curve of SN←Cy versus N radius exhibited a valley, but SN←CS increased (Supplemental Figs. 2A and 2B), whereas for a single cell with a constant N radius, as the cell radius increased, both SN←Cy and SN←CS decreased (Supplemental Figs. 2C and 2D). These observations were in good agreement with the published MIRD reports and MIRDcell-calculated values (15,16). The relative differences of mean MCNP-calculated versus MIRDcell-calculated Scross for monolayer or sphere were 26%–31% and 30%–34%, respectively. Scross depended on the location of the cell within the monolayer or sphere (Figs. 2A and 2B). MCNP-calculated mean Scross values were consistently larger than those calculated using MIRDcell. However, maximum and minimum Scross by MCNP, as well as mean Scross by MIRDcell, only slightly depended on the subcellular location of 64Cu and the radius of the cell N with the maximum difference observed of 18% and 11% for MCNP and MIRDcell, respectively, both from the smallest RC and the smallest RN calculated (5 and 2 μm), but these differences decreased as the cell radius increased. Scross decreased as the cell radius increased, following the equation of Scross = constant/RC3 (Fig. 2).
Effect of cell radius and subcellular location of 64Cu on maximum, minimum, and mean Scross values for cells within monolayer (0.2-mm-diameter circle) (A) and cluster (0.5-mm-diameter sphere) (B) calculated with MCNP and MIRDcell.
S Values for 64Cu Under Different Experimental Conditions
The mean S values for 64Cu uniformly distributed in subcellular compartments of a monolayer of cells with RC of 5–12 μm in a single well of a 96-, 48-, 24-, 12-, or 6-well plate were calculated, then the Scross values were derived by subtracting the self-dose S values from the calculated mean monolayer cell S values. The mean Scross only slightly decreased (<3.2% difference between 96-well and 6-well plates) as the well size decreased (Supplemental Table 4). To examine whether the subcellular location of 64Cu has an effect on the S values, the ratio of mean SN←N versus SN←Cy and SN←Cy versus SN←CS was calculated and plotted versus the ratio of RN versus RC for a single cell or a monolayer of cells in a 6-well plate (Figs. 3A and 3B). Both ratios decreased as the ratio of RC/RN increased. The ratio of mean SN←N versus SN←Cy was much greater than that of SN←Cy versus SN←CS, and the difference became larger as RC/RN decreased. S values and Scross for 64Cu uniformly distributed in subcellular compartments in a spheric cell cluster (radius of 0.05, 0.1, 0.25, 0.5, 1.5, or 6.0 mm) composed of cells with RC of 5–12 μm were calculated. The mean Scross increased as the cluster size increased and RC decreased (Supplemental Table 5), in accordance with the increased number of cells within the cluster, as listed in Supplemental Table 6. To again examine whether subcellular location of 64Cu has an effect on the S value, the ratio of mean SN←N versus SN←Cy and SN←Cy versus SN←CS was calculated and plotted versus RN/RC (Figs. 3C and 3D). Only for the smaller spheres (e.g., radius = 50, 100, 250, and 500 μm) and RN/RC ratio less than 0.5 would 64Cu located in the N deposit at least 1.5 times absorbed dose to the N than 64Cu in the Cy. The S value to the N for 64Cu uniformly distributed in 2-mm water (simulating non–cell-bound 64Cu) was also determined (Supplemental Table 7).
Plots of SN←N/SN←Cy and SN←Cy/SN←CS against RN/RC for single cell (A), monolayer cells in 6-well plate (B), and spheres (C and D) with radii of 50, 100, 250, 500, 1,500, and 6,000 μm, demonstrating effect of subcellular location of 64Cu on S values.
Contribution of Radiation Emissions to Sself and Scross Values
The contributions of γ-photon, β− particle, positron, and Auger/IC electron emissions from 64Cu to the Sself and Scross values are shown in Supplemental Tables 8 and 9, respectively. For a single cell, the Auger/IC electrons contributed most to SN←N (53%–84%), followed by β− particles, positrons, and γ-photons, whereas the β− particles were mainly responsible for SN←Cy (45%–70%) and SN←CS (73%–77%). The positrons also contributed to SN←Cy (13%–21%) and SN←CS (21%–24%). For a monolayer of cells attached to a well in a plate or a cluster of cells, the largest contributor to the Scross were the β− particles (67.3%–82.1%), followed by the positrons (28.9%–30.9%) and γ-photons (0.8%–1.1%). As the size of monolayer or cluster increased, the relative contribution of β− particles to Scross decreased, whereas the contribution of positrons and γ-photons increased. Figure 4 shows that the Scross from β+, β−, and γ-photons increased with the radius of the 18-μm-diameter cell cluster, though the slope became smaller except that Scross from the γ-photons continued to increase linearly with the cell cluster radius.
Dependence of mean Scross values by sum or individual contributions of different forms of radiation emitted by 64Cu on radii of spheric cluster composed of closely packed 18-μm-diameter cells.
Clonogenic Survival Curve
The clonogenic survival of MCF7/HER2-18 cells exposed to 1.9 mL of 64Cu-DOTA-trastuzumab (0–0.368 MBq/μg, 67 nM) for 18 h was determined. The subcellular distribution of 64Cu in MCF7/HER2-18 cells incubated with 64Cu-DOTA-trastuzumab (0.245 MBq/μg, 67 nM) for 1, 3, 15, and 18 h or treated similarly for 18 h, followed by culturing in fresh medium for 9.5, 22.5, 30, and 50 h, is shown in Figures 5A and 5B. Table 1 provides the time-integrated activity, Ã, in each source compartment (medium, CS, Cy, or N) for the 18-h incubation period, and the 10-d period allowed for colony formation. The radiation absorbed dose deposited in the N was calculated to be 3.8 ± 0.1 Gy (Table 1). The dose deposited in the N of MCF7/HER2-18 cells treated with the same concentration (67 nM) of 64Cu-DOTA-trastuzumab but different specific radioactivities (0.016, 0.031, 0.061, 0.123, and 0.368 MBq/μg) was estimated to be 0.23, 0.46, 0.93, 1.86, and 5.57 Gy assuming the same cellular uptake and efflux of trastuzumab. The SF versus the calculated absorbed dose to the N was plotted (Fig. 5C) and found to fit better to a linear survival curve, with an α = 0.51 ± 0.05 Gy−1 and R2 = 0.8838, than a linear quadratic model. This survival curve was significantly different from the previously reported survival curve of MCF7/HER2-18 cells exposed to γ-rays, which was best fit with a linear quadratic curve with an α and β of 0.823 Gy−1 and 0.02633 Gy−2 (19).
Subcellular uptake (A) and efflux (B) of 64Cu by MCF7/HER2-18 cells incubated with 64Cu-DOTA-trastuzumab (0.245 MBq/μg, 67 nM) as function of incubation time. Inset shows 64Cu effluxed into medium. Integrated activity in each cell compartment was calculated from area under curve and was used for estimating absorbed dose to cell nucleus. (C) Survival curves of MCF7/HER2-18 cells treated with 64Cu-DOTA-trastuzumab (0–0.368 MBq/μg, 67 nM) for 18 h in comparison to previously reported survival curve for MCF7/HER2-18 cells exposed to γ-rays (19).
Estimate of Absorbed Dose to N of MCF7/HER2-18 Cells Exposed to 64Cu-DOTA-Trastuzumab (0.245 MBq/μg, 67 nM) for 18 Hours, Followed by Clonogenic Assay
DISCUSSION
In this study, we calculated S values for 64Cu in a single cell, monolayer, or cell cluster geometry by MCNP simulation (14) and compared these values with those calculated by MIRDcell (16) or with the published cellular MIRD S values (15). Monolayer geometry is relevant to the treatment of cancer cells in vitro in a multiwell plate, whereas the cell cluster geometry applies to in vitro spheroids and in vivo treatment of tumor xenografts in mice. Although S values for single cell dosimetry (15) and organ macrodosimetry in humans (22), rats (23), or mice (24) have been published, our report is the first, to our knowledge, to describe S values for 64Cu in a monolayer or cell cluster geometry. In a previous study, we found that MCNP simulation was an accurate and reliable method to assess the cellular and subcellular radiation absorbed doses from the Auger electron–emitting radionuclide 111In in monolayer or cell cluster (17). MCNP-calculated S values for a monolayer predicted the SF of MDA-MB-468 cells exposed in vitro to 111In-diethylenetriaminepentaacetic acid human epidermal growth factor based on the survival obtained by γ-radiation exposure at similar calculated doses. To assess the accuracy of MCNP for calculating the S values for 64Cu, we first determined whether the MCNP-calculated Sself value agreed with those calculated by MIRDcell or published MIRD S values. There was good agreement between the MCNP-calculated and MIRD S values (Supplemental Table 1). We now report a comparison of the Scross for 64Cu calculated by MCNP or MIRDcell for cubically closely packed circular (diameter = 0.2 mm) monolayer and spheric (diameter = 0.5 mm) cluster cells (Supplemental Tables 2 and 3) by varying RC and RN from 5 to 12 μm and 2 to 11 μm, respectively. MCNP-calculated mean Scross values were 25.8%–30.6% and 30%–34% larger than those calculated by MIRDcell for a monolayer and cluster, respectively. This was probably due to inclusion of the γ-photons in the MCNP calculation, which were ignored by MIRDcell, the difference in electron spectra, the composition of materials used, and the different calculation approach applied by MCNP and MIRDcell. Using 0.2-mm-diameter monolayer cells with RC of 10 μm and RN of 8 μm as an example, we calculated the Scross for each of the 69 cells one by one with the same electron spectrum used by MIRDcell, defining the material of cell and cell N as water, as MIRDcell does. The average of 69 calculated Scross values (Supplemental Fig. 3A) was 0.068 mGyBq−1s−1, still 25.9% larger than the value obtained by MIRDcell. In contrast, this value was only 1.4% lower than the mean Scross value, suggesting that the difference was due to the different calculation approach applied. MCNP is based on Monte Carlo simulation and allows the transport of radiation through a 3-dimensional geometry, whereas MIRDcell uses the analytic method and propagates electrons in straight trajectories. Falzone et al. found that when the source was farther from the target region, the difference between cellular S values for Auger-emitting radionuclides calculated from PENELOPE Monte Carlo simulation and the MIRD method tended to increase (25).
The packing density of tumor cells in monolayer or cluster also has an effect on Scross. The hexagonal closely packed spheres account for 74.0% of the cluster volume and 90.7% of the monolayer area, whereas closely packed spheres in a simple cubic lattice account for only 52.4% of the volume and 78.5% of the area. Higher packing density means more cells are included in the defined cluster or monolayer. Because this study assumed that 64Cu was homogeneously distributed in each cell compartment, Scross calculated using hexagonal closely packed spheres would be higher than that calculated using a cubic lattice. There are 2 reasons that we chose a cubic lattice to calculate S values: a cubic lattice is used in MIRDcell and the subconfluent monolayer cells normally occupy no more than 75% of the well area and seldom reaches 90%. Depending on the cell lines, the cell packing density both in vitro and in vivo varies but seldom reaches the highest possible density. Ideally the Scross should be calculated on the basis of the known cell packing density. For dose estimation in the clonogenic assay of MCF7/HER2-18 cells, the S values were calculated on the basis of the measured cell number (7 × 105 cells per well) in a 6-well plate, which occupied only about 25% of the well area.
With positive verification of the MCNP calculation with MIRDcell, we then used MCNP to determine cellular S and Scross values for monolayer cells on 96-, 48-, 24-, 12-, and 6-well plates and in a spheric cell cluster of the size (diameter of 0.1–12 mm) equivalent to a micrometastasis and typical mouse tumor xenografts (Supplemental Tables 4 and 5; Fig. 4). We also calculated the S value for 64Cu uniformly distributed in 2-mm-thick water sufficient to cover cells in a well (Supplemental Table 7). These S values help to accurately calculate the absorbed doses to the cell N for cells exposed to 64Cu-labeled radiopharmaceuticals during in vitro and in vivo cytotoxicity studies. Our results also inform on the design of these experiments. For example, the well size of the tissue culture plate for in vitro cytotoxicity assays is not an important factor for 64Cu bound to cells, because this does not affect the absorbed doses delivered to the N. In vivo, the size of tumor xenograft needs to be considered when the therapeutic effect of 64Cu agents are evaluated (Fig. 4). If the tumor is a sphere with a diameter greater than 3.0 mm, the tumor size has less effect on the absorbed dose. However, if tumor diameter is less than 3.0 mm and the time-integrated activity per tumor cell is the same, the dose decreases as tumor size decreases, due to the decreased contribution of the cross-dose.
We next examined whether the subcellular location of 64Cu has an effect on the S values (Fig. 3) for a single cell, cells in a plate, or cells in a tumor xenograft. We found that the effect of subcellular location on S values was more pronounced for cells with a smaller RN-to-RC ratio, a single cell, followed by monolayer and small cluster cells. With the same RN-to-RC ratio, SN←N/SN←Cy is always far larger than SN←Cy/SN←CS. Our results suggest that for treatment of a tumor greater than 1 mm in diameter with 64Cu, it would be sufficient to simply target the tumor cells, but there would not be substantial benefit to route 64Cu to the Cy or N. For treating a micrometastasis, however, it would be advantageous targeting the N to increase the dose deposited. The effect of 64Cu subcellular location on the radiotoxicity observed in vitro would not be representative for a tumor larger than 1 mm in vivo.
We then examined the contribution of each radiation type to S values for a single cell, monolayer, or cluster of cells (Supplemental Tables 8 and 9). For a single cell, the subcellular location of 64Cu was important for all the S values, because Auger/IC electrons contribute most to SN←N (53%–84%) and substantially to SN←Cy (8.2%–42%). For cells in a monolayer or in a sphere, the main contributors to the cross-dose were β− particles, followed by positron, whereas Auger/IC electrons contributed 0.05%–5% to the Scross value. Thus, only when the self-dose from Auger/IC electrons outweighed the cross-dose did the subcellular location of 64Cu have an effect on the overall radiation dose deposited. Only for monolayer and a sphere with a diameter less than 1 mm did the subcellular location of 64Cu have an effect on S values (Fig. 3).
Finally, we calculated the absorbed dose to the N of MCF7/HER2-18 cells during 18-h exposure to 64Cu-DOTA-trastuzumab and 10-d colony formation using the respective mean S values for monolayer cells and a single cell obtained by MCNP calculations as well as the time-integrated activity estimated from the uptake and efflux experiments. The absorbed doses to the N ranged from 0.23 to 5.57 Gy depending on the specific radioactivities of 64Cu-DOTA-trastuzumab (0.016–0.368 MBq/μg). At the highest dose, the SF was 0.10 ± 0.02. Eiblmaier et al. (26) estimated the dose to the cell and N of A427-7 cells exposed to 64Cu-TETA-Y3-TATE or 64Cu-CB-TE2A-Y3-TATE using only the self-dose S value, as less than 1 Gy and 0.3 Gy, respectively, even if using high-specific-radioactivity radiopeptides (37 MBq/μg). Thus, they did not pursue further cytotoxicity experiments. However, these doses were underestimated using the self-dose S value instead of the much larger mean monolayer S values determined in our study.
We found that the survival curve of MCF7/HER2-18 cells exposed to 64Cu-DOTA-trastuzumab in vitro in wells of a 6-well plate followed a linear model, which was significantly different from the previously reported survival curve of MCF7/HER2-18 cells exposed to γ-rays (Fig. 5C) (19), which was best fit by a linear quadratic curve. Moreover, as the dose increased, the difference between the 2 survival curves became more evident. At the same mean dose, 64Cu appeared to be less cytotoxic than γ-rays. The heterogeneous distribution of 64Cu-DOTA-trastuzumab bound to cells (e.g., normal or lognormal distribution) and cross-doses to cells (higher cross-dose to cells closer to the center of the well or sphere (Supplemental Fig. 3), as well as the much lower dose rates than γ-rays might account for the difference in survival curves.
CONCLUSION
S values of 64Cu for closely packed monolayer and cluster cells reported here represent a valuable new contribution for dose estimation in the therapeutic application of 64Cu that inform on the design of both in vitro and in vivo experiments. MCNP- and MIRDcell-calculated S values were in good agreement. Targeting 64Cu into the cell N maximizes the dose to the N in isolated single tumor cells but has less effect in a cell monolayer and little effect in a sphere analogous to a tumor xenograft. 64Cu appeared to be less cytotoxic than γ-rays.
DISCLOSURE
This study was supported by a grant from the Canadian Cancer Society Research Institute (grant #701682) with funds from the Canadian Cancer Society. Yongkyu Luke Kwon received a scholarship from the Canadian Institutes of Health Research Training Program in Biological Therapeutics and a MDS Nordion Scholarship. No other potential conflict of interest relevant to this article was reported.
Footnotes
Published online Sep. 22, 2016.
- © 2017 by the Society of Nuclear Medicine and Molecular Imaging.
REFERENCES
- Received for publication March 14, 2016.
- Accepted for publication September 1, 2016.












