Abstract
Patients undergoing nuclear medicine procedures for cancer therapy are administered radiopharmaceuticals that emit various types of radiation. Because radiation has differential delivery to and uptake by cells in tissue, radiation exposures are often highly nonuniform. Some cell populations in a tissue may contain widely different amounts of radioactivity, whereas other cell populations in the same tissue may contain no radioactivity, referred to as labeled and unlabeled cells, respectively. Furthermore, the toxicity of the radiations emitted can depend on the location of the radioactive decay within the cell (e.g., nucleus vs. cytoplasm). Therefore, the response of a given cell depends on the absorbed dose received from radiations emitted by decays within the cell (self-dose) and emitted by decays in neighboring cells (cross-dose), among other factors. Taken together, these variables make it difficult to predict the response of cell populations to radiopharmaceuticals. Accordingly, to assist in designing treatment plans for therapeutic radiopharmaceuticals, an applet software application called MIRDcell was developed. This applet models the distribution of radiopharmaceuticals in tissues, calculates the distribution of radiation dose, models responses on a cell-by-cell basis, and predicts the surviving fraction of the labeled and unlabeled cell populations. MIRDcell can be accessed at http://mirdcell.njms.rutgers.edu/.
Prediction of tumor and normal-tissue responses in therapeutic nuclear medicine relies heavily on calculation of the absorbed dose. However, absorbed-dose specification is complex because of the wide variety of radiations emitted, heterogeneity in activity distribution, biokinetics, and other confounding factors (1). After the administration of a radiopharmaceutical, the radioactivity is taken up by tumors (if any) and the various organs within the body, and the radioactivity is then eliminated through both biologic clearance and physical decay. A general formalism was developed by the MIRD Committee of the Society of Nuclear Medicine and Molecular Imaging to calculate absorbed doses from tissue-incorporated radioactivity (2). Conventional organ absorbed-dose estimates assumed that the radioactivity was distributed uniformly throughout the organ and that the mean absorbed dose to the organ was being calculated. However, there have been dramatic improvements in dosimetry models that reflect the substructure of organs as well as tissue elements within them (3–5). These models rely on improved nuclear medicine imaging capabilities that facilitate determination of activity within the voxels that represent tissue elements that are about 0.2–1 cm3 in volume (6–9). However, even these improved approaches assume that all cells within the tissue element receive essentially the same absorbed dose. The tissue element may comprise a variety of cells having very different radiosensitivities (10) and sometimes, depending on the radiopharmaceutical, very different levels of incorporated radioactivity (11,12). Accordingly, the absorbed dose delivered to the various cells in the tissue element and their response may differ markedly. Therefore, a combination of voxel-, cellular-, and multicellular-level dosimetry is required to accurately predict biologic response to nonuniform distributions of radioactivity (1,13).
The extent to which nonuniform distributions of radioactivity within a small tissue element affect the absorbed dose distribution, and ultimately the biologic effect, is strongly dependent on the number, type, and energy of the radiations emitted by the radionuclide. Many radionuclides used in nuclear medicine decay by electron capture or internal conversion (e.g., 67Ga, 99mTc, 111In, 123I, and 201Tl) and consequently emit a large number of low-energy Auger and conversion electrons. Many of these electrons deposit their energy over subcellular dimensions and therefore produce nonuniform dose distributions (14,15). Similarly, the short range of α particles in biologic tissues (40–100 μm) also leads to nonuniform dose distributions from 223Ra and other α-particle emitters of potential use in nuclear medicine (15–20). Energetic β emitters such as 90Y have a greater degree of cross-irradiation because their mean range in tissue is at least several hundred microns. However, the nonuniform distribution of these radionuclides invariably leads to nonuniform dose distributions as well (21–25). Although it is essential to consider the dose distributions that arise from nonuniform distributions of radioactivity, it is also necessary to know whether the dose to a given cell arises from radioactive decays within itself (self-dose) or decays in surrounding cells or other parts of the body (cross-dose). Cellular response to self-dose delivered by a radiopharmaceutical can be considerably different from its response to cross-dose from the same radiopharmaceutical. This is well known for Auger emitters, for which—depending on the subcellular distribution of the radiopharmaceutical—the relative biological effectiveness of the self-dose can be an order of magnitude greater than that of the cross-dose (26). This has been observed for β emitters as well, for which the self-dose from 131I was shown to be 3 times more lethal than the cross-dose (27).
There is a growing body of experimental data on the biologic effects of nonuniform distributions of radioactivity at the multicellular level. Detailed studies have been performed in which varying proportions (from 1% to 100%) of a 3-dimensional (3-D) population of mammalian cells were radiolabeled with 125I (28), 131I (27,29), or 210Po (30). In the case of 210Po and 131I, survival curves for 10% labeling were concave upward despite the high degree of cross-irradiation delivered under these conditions. The survival curve for 100% labeling with 210Po also was somewhat concave upward (30). These complex responses can be attributed, in part, to the nonuniform distribution of activity in these multicellular structures (31,32). These findings can have significant consequences for therapeutic uses of these and other radionuclides. Accordingly, there is a need for software tools that can model biologic responses to nonuniform activity distributions encountered in nuclear medicine. The software, MIRDcell, described in this pamphlet provides tools that can be used to assist in designing nuclear medicine treatment strategies.
MATERIALS AND METHODS
In collaboration with the MIRD Committee of the Society of Nuclear Medicine and Molecular Imaging, Rutgers University created a Java applet to provide worldwide access (http://mirdcell.njms.rutgers.edu/) to new software that facilitates multicellular dosimetry and biologic-response modeling. A graphical user interface consisting of a multitabbed pane was generated. Under each tab, the user can select the values of variables that are used to model radiation dose and response in 2-dimensional (2-D) and 3-D cell populations. 2-D cell populations are constrained to lie on a plane (e.g., monolayer cell cultures, cells on bone surface). Provision is also made for calculation of self- and cross-dose S values for a pair of cells that are referred to as 1-dimensional (1-D). The organization of the tabs and options within each tab are provided in an online data supplement available at http://jnm.snmjournals.org. Although most of the options are self-explanatory, some features are explained below. Nomenclature is consistent with MIRD pamphlet no. 21 (33). The computational speed of MIRDcell is strongly coupled to computing power; version 2.0 (V2.0) should be run on a processor equal to or better than an Intel i5. The Java control panel should be used to increase memory allocation to 1,024 MB and to add http://mirdcell.njms.rutgers.edu to the exception list on the security tab. The computing power required is proportional to the number of cells in the multicellular cluster. Details regarding the computational platform requirements and several benchmark computational times are provided in the online supplemental data.
“Source Radiation” Tab (Fig. 1)
The “Source Radiation” tab allows the user to select the radioactivity in the source cells (i.e., cells labeled with radioactivity). After a selection is made, the radiation data are shown in the box entitled “Input Data for Calculation.” Three choices are available, including a predefined MIRD radionuclide, a monoenergetic particle emitter, and a user-defined radionuclide.
Screenshot of “Source Radiation” tab. This tab provides 3 options for selecting radioactivity to be placed in labeled cells: (1) Predefined MIRD radionuclide (top left). Radiation spectra are available for predefined radionuclides that include average β-particle energies (“β Average Energy Spectrum”) or complete β-particle spectrum (“β Full Energy Spectrum”). (2) Monoenergetic particle emitter (top right). Here, user can select either α particle or electron and can specify particle yield per disintegration and energy. (3) User-created radionuclide (lower left). User can create a radionuclide that includes a variety of selectable radiations (α, Auger electron, β−, and β+). Data are streamed into bottom right box, input data for calculation.
There are 2 options within the predefined MIRD radionuclide. The “β Full Energy Spectrum” option provides a dropdown list of the radionuclides for which data are provided in the MIRD monograph on radionuclide data and decay schemes (34). The datasets correspond to the radiation data that were used to prepare the monograph; however, the yield and mean energies for all β-particle (β−) and positron (β+) emitters were replaced with full logarithmically binned β spectra. Use of the continuous β spectrum as opposed to the mean β energy can play an important role in cellular dosimetry (35); however, there can be a considerable increase in computation time when the former is used. This altered dataset was originally created for calculating cellular S values in the MIRD monograph on that topic (35). Some of the spectra contained in excess of 1,000 different radiations for a given radionuclide, many of which are insignificant with respect to internal dosimetry. Therefore, only those radiations that contributed greater than 0.1% to the total energy emitted per nuclear transformation (Δ) for that particular radiation type were retained. The different radiation types considered separately in this manner were α particles and conversion electrons. However, the 0.1% cutoff was implemented neither for the spectrum of β particles nor for Auger electrons. The recoil energy of the residual daughter after α decay was not included because experiments indicate that this energy is not biologically relevant (36). The “β Average Energy Spectrum” option provides the radiation data contained on the compact disk that accompanies the second edition of MIRD: Radionuclide Data and Decay Schemes (37). Average β-particle energies are contained within this dataset.
Extreme care must be exercised when conducting calculations for radionuclides that are part of a decay chain (e.g., 211At, 213Bi, 223Ra, and 225Ac). Unless specifically stated in the predefined dropdown menu, the radiations listed for a given radionuclide do not include radiations emitted by descendant (i.e., daughter) radionuclides. Depending on the half-life of the descendant, it may diffuse away from the site of parent decay and have a cell-level distribution and kinetic profile that differs substantially from that of the parent. Users can create files that include daughters, provided that branching ratios are accounted for (online supplement). However, this should be done only when the descendant radionuclides either are known to be retained at the site of parent decay or can be assumed to do so on the basis of half-life.
The “Monoenergetic Particle Emitter” option allows the user to select a hypothetical monoenergetic electron or α-particle emitter. Particle energy and yield per nuclear transformation are specified by the user.
The “User Created Radionuclide” option provides maximum flexibility by allowing the user to create a radionuclide that is not available in the predefined dropdown lists. After specifying the name of the radionuclide, the user chooses radiation type, its yield, and its energy and then clicks “Add Radiation.” This process is repeated until all desired radiations have been added. “Confirm List of Radiations” is then clicked. If it is desired to save the radionuclide for later use, the user clicks “Save” and the radionuclide will be saved to a local storage location.
Finally, once the user selects the desired radionuclide from one of the 3 options above, the radiation data stream into the box entitled, “Input Data for Calculation.” Specified in descending order are the radionuclide, physical half-life, and principal decay type. This is followed by the radiation data for the radionuclide; these include the total number of radiations in the file and the radiation type, yield, energy, and mean energy emitted per nuclear transition for each radiation Δi.
“Cell Source/Target” Tab (Fig. 2)
As described in detail by Goddu et al. (38) and the MIRD monograph on cellular S values (35), the cell is modeled as 2 concentric spheres with radii corresponding to those for the nucleus (RN) and cell (RC). The cells are assumed to be composed of liquid water of unit density. The radioactivity in the cell is assumed to be uniformly distributed in the source region of the cell, selectable among cell (C), cell nucleus (N), cytoplasm (Cy), or cell surface (CS). The target region in the cell for which the absorbed radiation dose will be calculated can be selected as either the entire cell or the cell nucleus. The radii of the cell and cell nucleus are limited to integer values and are specified by the user. The minimum cell size is RC = 2 μm, RN = 1 μm. No limit has been set on the maximum cell size; however, extensive testing has been conducted only up to RC = 10 μm. Although we believe that the algorithms should be adequate for calculating absorbed doses to much larger cells (i.e., spheres), caution should be exercised when interpreting results for RC > 10 μm.
Screenshot of “Cell Source/Target” tab. Source region (red) in cell that contains radiopharmaceutical can be selected as cell, cell surface, nucleus, or cytoplasm (top left). Selectable target regions (blue) include cell, nucleus, or cytoplasm (top left). Cell and cell nucleus are represented by concentric shells of unit density water with cell radius (RC) and cell nucleus radius (RN), which can be set as desired (bottom left).
“Radiobiologic Parameters” Tab (Not Shown)
MIRDcell enables the user to model the surviving fraction of cells in a specified cell population based on the calculated absorbed doses to the individual cells. Similar to the approach used by Rajon et al. (32) and Akudugu et al. (39), the probability that a given cell survives is calculated with the linear quadratic model (Eq. 1),
Eq. 1where αself and βself are the linear quadratic parameters that characterize the cellular response to self-dose (Dself) and αcross and βcross characterize the cellular response to cross-dose (Dcross) (15,27,40). This distinction can often be necessary for Auger electron emitters (28), or even β-particle emitters (27), when they are incorporated into the DNA. Under these circumstances, the relative biological effectiveness of Auger emitters can be akin to α particles (28). The default parameters are set to αself = αcross = 1 Gy−1, and βself = βcross = 0 Gy−2. These default values are arbitrary and the user is cautioned to enter values that are relevant to their application. Whether a given cell survives is determined by a Monte Carlo method that is described below in “Multicellular Geometry < 2-D Colony < Surviving Fraction.”
“Multicellular Geometry” Tab
“Multicellular Geometry < 1-D Cell Pair” Tab (Fig. 3)
Figure 3 depicts the cell geometry that is used to calculate the self- and cross-doses for a pair of cells. This configuration is considered 1-D. The source and target volumes are color-coded: the radioactivity-containing source volume is red, and the target volume in the neighboring cell is blue. The user sets the distance (d) between the centers of 2 cells that are nearest neighbors. The self-dose and cross-dose S values (mean absorbed dose per unit cumulated activity in the source region) for the specified source and target regions are calculated when the “Compute” button is clicked. The self-dose and cross-dose S values are calculated using stopping powers and geometric factors as described in the MIRD monograph on cellular S values (35,38) and by Goddu et al. (15), respectively. As in the MIRD monograph, the stopping power relationship of Cole was used for electrons, and α-particle stopping powers were taken from reports of the International Commission on Radiation Units and Measurements (41). This computational approach was previously validated by the MIRD Committee by comparison with results obtained with the EGS4 Monte Carlo radiation transport code (35). New Monte Carlo radiation transport codes have recently been developed for low-energy electrons (42); their self-dose S values can vary significantly from those calculated with MIRDcell V2.0 for low-energy Auger electron emitters such as 125I localized on the cell surface or cytoplasm.
Screenshot of “Multicellular Geometry < 1-D Cell Pair.” This subtab enables rapid calculation of self-dose to labeled cell and cross-dose to neighboring cell that lies at some distance (i.e., 16 μm between centers in this example). Self- and cross-doses per unit cumulated activity in source cell (Gy Bq−1 s−1), also known as S value (2,35), are reported for selected source radiation (i.e., 90Y in this example) in box labeled “Result.” Calculation can be repeated for different cell separation distances (top left).
“Multicellular Geometry < 2-D Colony < 2-D Colony” Tab (Fig. 4A)
This option is used to create a cell population that resides on a plane (i.e., colony). In the “Cell Geometry” box, the user specifies the distance between the cells and the shape and dimensions of the colony (circle, rectangle, ellipse). In the “Cell Labeling” box, the user selects the distribution of activity among the labeled cell population (uniform, normal, lognormal) and enters the SD of the mean for the normal distribution or shape factor for the lognormal distribution. A uniform activity distribution among the labeled cells implies that each labeled cell has the same initial activity A in its source region (Fig. 4B). In the normal distribution, the initial activity per cell is distributed according to the probability density function: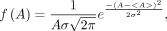
Eq. 2where <A> is the mean initial activity per cell and σ is the SD of the mean. A conscious effort is required by the user to avoid entering an SD that can result in negative values of A. When this occurs, the user is prompted to choose a smaller value for σ. In the case of the lognormal distribution, the activity per cell is distributed according to the probability density function:
Eq. 3where σ is the lognormal shape parameter. Thus, if <A> is known experimentally, then only σ is required. “Mean Activity per Cell” (labeled + unlabeled) and time-integrated activity coefficient (ã) are then entered. The time-integrated activity coefficient is defined in MIRD pamphlet no. 21 (33). The user then specifies the “Percentage of Cells That Are Labeled” with radioactivity. Once all the parameters are specified, the user clicks the “Compute” button. Calculation times vary dramatically depending on the number of radiations emitted by the selected radionuclide, the range of the particles emitted, and the percentage of cells that are labeled. A progress bar appears below the “Compute” button to provide the status of the calculation. Progress for part 1 corresponds to the calculation of all necessary self- and cross-dose S values. Progress for part 2 corresponds to the process of creating a virtual assembly of cells in a Cartesian coordinate system with a close-packed square lattice (number of cells is displayed), assigning activity to each cell, tallying self- and cross-doses for each cell, calculating the surviving fraction of cells, and plotting the colony geometry in the graphical user interface. Labeled cells are selected randomly, and each cell is randomly assigned an initial activity according to a user-selected distribution. The time-integrated activity in the source compartment of each cell is calculated by taking the product of the initial activity in the cell and the user-specified time-integrated activity coefficient (ã). The activity in all labeled cells is assumed to have the same time-integrated activity coefficient, formerly known as the residence time (τ). The algorithms for these computations have been described by Howell et al. (31).
Screenshots of “Multicellular Geometry < 2-D Colony < 2-D Colony.” (A) Here, user can select multicellular geometry wherein cell population lies on plane. In “Cell Geometry” box, cell population can be constrained to different selectable shapes including circle (shown), ellipse, and rectangle (top left). Dimensions of each shape are provided by user (i.e., circle with 66-μm radius in this example). In “Cell Labeling” box, activity can be distributed among cell population according to selectable labeling methods: uniform (shown), normal, and lognormal. Mean activity per cell, residence time, and percentage of cells that are labeled can be specified. On selecting parameters and clicking “Compute,” resulting multicellular geometry is plotted on right in a manner that indicates whether cell is labeled (red) or unlabeled (green), and transparency represents whether cell is dead (transparent) or alive (opaque). (B) Histogram of activity per cell. This example shows uniform distribution of activity among labeled cells (each labeled cell has same activity). (C) Plot of surviving fraction of cells.
“Multicellular Geometry < 2-D Colony < Activity Distribution Histogram” Tab (Fig. 4B)
The user-specified activity distribution is plotted in this tab.
“Multicellular Geometry < 2-D Colony < Surviving Fraction” Tab (Fig. 4C)
Also calculated on clicking the “Compute” button is the surviving fraction of cells in the colony. The surviving fraction is calculated using the Monte Carlo method described by Howell et al. (31). Briefly, for each cell, a survival probability is calculated by substituting the self-dose and cross-dose that are calculated specifically for that cell into Equation 1. A random number between 0.0 and 1.0 is generated (Java class java.util.Random; it uses a 48-bit seed, which is modified using a linear congruential formula) and compared with the survival probability. If the random number was smaller than the generated probability, the cell was scored as a survivor. Otherwise, it was scored as dead (i.e., having undergone reproductive failure). This process is then repeated for every cell in the population. The fraction of survivors among the cell population that composes a given simulation represents the surviving fraction of the cell population. This entire process is repeated for numerous values of <A> up to a maximum value corresponding to the user-assigned mean activity per cell. The resulting surviving fractions are plotted as a function of cellular activity or absorbed dose to the labeled, unlabeled, and entire cell population according to user-selectable ordinates and abscissae. These choices allow the user to explore the characteristics of the response of each population of cells. Labeled cells receive both self-dose and cross-dose, whereas unlabeled cells receive only cross-dose.
“Multicellular Geometry < 3-D Cluster < 3-D Cluster” Tab (Fig. 5)
The planar cell configuration described above is extended to 3-D clusters as shown in Figure 5A. The user selects the shape of the cluster: sphere, ellipsoid, rod, or cone (Fig. 6). The desired dimensions of the cluster are then entered along with the time-integrated activity coefficient (ã), mean activity per cell (labeled + unlabeled cells), and percentage of cells labeled. When the user clicks the “Compute” button, the simulation and modeling begin. The process is essentially the same as for the 2-D colony except that the cluster is assembled in a 3-D Cartesian coordinate system in a close-packed cubic lattice. As in the 2-D colony case, the user-specified activity distribution is plotted in the “Activity Distribution Histogram” tab (Fig. 5B). Survival curves are provided in the “Surviving Fraction” tab (Fig. 5C).
Screenshot of “Multicellular Geometry < 3-D Cluster < 3-D Cluster.” (A) User can select multicellular geometry wherein cell population is contained within 3-D geometry. In “Cell Geometry” box, cell population can be constrained to different selectable shapes including sphere (shown), ellipsoid, and cone. Dimensions of each shape are provided by user (i.e., sphere with 65-μm radius in this example). In “Cell Labeling” box, activity can be distributed among cell population according to selectable labeling distributions: uniform, normal, and lognormal (shown). Mean activity per cell, residence time, and percentage of cells that are labeled can be specified. When parameters are selected and “Compute” is clicked, the resulting multicellular geometry is plotted on right in a manner that indicates whether cell is labeled (red) or unlabeled (green), and transparency represents whether cell is dead (transparent) or alive (opaque). (B) Histogram of activity per cell. Small number of labeled cells (in this case it is 172) magnifies stochastic aspects of distribution in such a small population. Repeated clicking of “Compute” tab shows variations in distribution when Monte Carlo calculations are repeated. (C) Plot of surviving fraction of cells.
Examples of additional geometries available in “Multicellular Geometry < 3-D Cluster < 3-D Cluster.” These are 3-D cluster shapes with 50% of cells labeled. Cluster shapes are sphere, rod, cone, and ellipsoid. Cells are labeled (red) or unlabeled (green), and transparency represents whether cell is dead (transparent) or alive (opaque).
“Output” Tab
Output data are written to 2 boxes in the “Output” tab; these data can be copied and pasted into other software applications. The left box contains information on the geometry of the cell population, the values of the various input parameters, and the calculated data used to create survival curves. The right output box contains a tabulation of the cellular self- and cross-dose S values for the various target and source volumes in cells having the dimensions selected in the “Cell Source/Target” tab. The top row provides the S values for a labeled cell. The cross-dose S values begin on the row corresponding to the minimum cell separation distance in micrometers. The online supplement provides instructions on cutting data from the output box and pasting into other software applications.
“Credits” Tab
This code has undergone various stages of development. Several publications emerged during this process, the first being that by Sastry et al. (43) describing a 3-D multicellular cluster of cells that were labeled on the cell surface by monoenergetic electron emitters. Howell et al. introduced additional capabilities, including different subcellular activity distributions and exponential radial distributions of activity (44). Goddu et al. introduced the concept of cellular S values, which were used to calculate self-dose (38). This was extended to cross-doses and used to calculate self-dose–to–cross-dose ratios for multicellular clusters containing a variety of radionuclides (15). Howell et al. introduced cell survival analysis into the code (31). Despite these improvements, the broad capabilities of the code were inaccessible to the scientific community because the FORTRAN language used before this report did not provide for robust graphical user interfaces. Accordingly, we translated the code to Java, wrote new code to provide additional capabilities, and developed a graphical user interface to make the software available on the Web.
DISCUSSION
MIRDcell V2.0 is a versatile platform that can be used to calculate the surviving fractions of cell populations that are labeled with radioactive materials. Although a large number of variables can be controlled by the user, there are many variables of physical and radiobiologic nature that are not. For example, the cell and cell nucleus are modeled as concentric spheres. Theoretic models have shown that the shape of the cell can have an impact on the calculated absorbed dose (45); however, the impact is typically small (35). MIRDcell V2.0 also assumes that all cells in the population are the same size. Charlton has demonstrated that the distribution of cell sizes and packing density can have some effect on the surviving fraction of spheric clusters of cells labeled with α-particle emitters (46), whereas Fisher and Harty showed that the location of the nucleus within the cell can influence the response to this class of radionuclides (47). Furthermore, in the case of α particles, for which only one to several traversals across the cell nucleus are generally required to kill a cell, there are stochastic variations in the number of decays, hits, and energy deposited (48), all of which can affect the surviving fraction. The present model, which uses S values for determination of absorbed dose, does not address these aspects, which can be addressed with microdosimetry (46,49,50). Those elements include the fine structure of secondary electrons (i.e., δ rays) and the stochastic nature of single-energy-deposition events. The impact of these variables on the surviving fraction is likely to be more significant when the number of cells in the population is small and when cross-doses are small relative to self-doses. MIRDcell V2.0 permits some evaluation of the stochastic nature of cell death for a given activity distribution. Repeatedly clicking on the “Compute” button causes both activity distribution and cell survival to be resimulated and the survival curve to change for each new simulation. Changes in response are most apparent when the survival curve approaches the point at which there are few survivors.
Also not accounted for explicitly in MIRDcell V2.0 is the dependence of the survival response on dose rate and its temporal changes. In targeted radionuclide therapy, dose rate kinetics are dictated by the biologic uptake and clearance of the radiopharmaceutical and physical decay of the radionuclide (51). However, in principle, this variable can be accounted for by entering appropriate values for the linear-quadratic model parameters in the “Radiobiology” tab of MIRDcell V2.0. Bystander, cohort, and abscopal effects are not explicitly modeled in this program (52). They can be of considerable importance in the context of targeted radionuclide therapy (53) and, more specifically, in the context of the algorithms used in MIRDcell V2.0 when small fractions of cells are labeled with α-particle emitters (31). Therefore, users of MIRDcell V2.0 should be cognizant that radiation-induced bystander effects might alter the results.
We have compared some of the results produced by MIRDcell V2.0 with those in the published literature—for example, in Table 1 of Charlton (46). The parameters were cells (n = 2,469) with a mean radius of approximately 6 μm packed into a 200-μm-diameter sphere with a packing density of 50%, 211At distributed uniformly among the cells, nucleus not modeled, and mean lethal dose D37 = 0.5 Gy (equal to 1/α when β = 0 in the linear quadratic model). Using these parameters as a guide, MIRDcell V2.0 was run with the following parameters: RN = 4 μm, RC = 6 μm, d = 12 μm, Target←Source = C←C, αself = αcross = 2 Gy−1, βself = βcross = 0, 3-D cluster, sphere with radius of 100 μm, uniform distribution, mean activity per cell of 0.0005 Bq, time-integrated activity coefficient (assuming no biologic clearance and complete decay) of 10.4 h, and 100% of cells labeled. The time-integrated activity coefficient was formerly known as the residence time (33). This results in a nearly exponential survival curve with D37 = 0.5 Gy, which corresponds closely to the results of Charlton (46). Similar comparisons have been made with the calculations described by Howell et al. (31), wherein 100%, 10%, or 1% of the cells in a multicellular cluster were labeled with the α-particle emitter 210Po. This comparison is described fully in worked example 2 in the online supplement. The survival curves calculated with MIRDcell V2.0 match those of Howell et al. (31). As shown in Figure 7, a comparison has also been made between these results from MIRDcell, version 2.0.13, and the corresponding experimental cell survival data in Neti and Howell (30). The correlation is very good, with the exception of 1% labeling at high activity per labeled cell. This was also observed by Howell et al. and may be due to a radiation-induced bystander effect (31). Application of MIRDcell V2.0 to several other experimental datasets can be found in the online supplement.
Comparison of experimental cell survival data (symbols) and theoretic cell survival data (solid lines; calculated with MIRDcell, version 2.0.9) for α-particle emitter 210Po in multicellular clusters. Experimental data are from Neti et al. (30), where 100%, 10%, or 1% of cells in cluster are labeled with 210Po. Inset shows full datasets for 1% labeling case. Modeling parameters are described fully in worked example 2 in online supplement.
CONCLUSION
Given the highly nonuniform cellular exposures received in nuclear medicine, designing treatment plans for therapeutic radiopharmaceuticals is challenging. Therefore, this applet was developed to allow users to visualize and understand the impact of radionuclide choice, distribution of activity in and among cells, cell dimensions, intercell distances, cluster size, and radiobiologic response parameters on the capacity to kill populations of cells. All these parameters can play a substantial role in determining the surviving fraction of cells. Accordingly, this applet can assist in designing treatment plans for therapeutic radiopharmaceuticals suited to individual needs.
DISCLOSURE
No potential conflict of interest relevant to this article was reported.
DISCLAIMER
This program is provided for educational purposes only. It has undergone a limited set of validation tests, but there is no guarantee or warranty of accuracy for any purpose expressed or implied. Any user of this program assumes any and all responsibility and liability for its use. Any use of this program is “as is” and should only follow the user’s independent confirmation that it produces valid results for the user. In no case shall the authors, Rutgers University, the MIRD Committee, or the Society of Nuclear Medicine and Molecular Imaging be liable for any incorrect or invalid results that are obtained by any use of this program, nor shall they be liable for any direct or indirect damages arising out of or in connection with the use or performance of this program. MIRDcell V2.0 has not undergone review by the United States Food and Drug Administration, and therefore this version of MIRDcell should not be used for human patients.
VERSION HISTORY
Version 2.0.15: April 26, 2014 (http://mirdcell.njms.rutgers.edu)
Version 2.0.13: February 14, 2014 (http://mirdcell.njms.rutgers.edu)
Version 2.0.6.1: July 18, 2013 (http://mirdcell.njms.rutgers.edu)
Version 2.0: September 6, 2012 (http://njmsweb04.umdnj.edu)
Version 1.1: March 21, 2012 (http://njmsweb04.umdnj.edu)
Version 1.0: December 23, 2010 (http://njmsweb04.umdnj.edu)
Acknowledgments
We are grateful to the many individuals who have developed different aspects of this code over many years: Chris Haydock (43), the late Kandula Sastry (43), Dandamudi Rao, Murty Goddu, Elizabeth Paul, and Rozana Rahman. We also greatly appreciate the efforts of Tom Bäck and Massimo Pinto, who tested the code and helped us troubleshoot problems related to locale-dependent data and services when using Java internationally. This work was supported in part by NIH R01CA083838. We thank Harvey Ozer and Gwendolyn Mahon for supporting BV in the Cancer Summer Student Research Program, supported by NCI 5R25CA019536-32.
Footnotes
Published online Jul. 10, 2014.
- © 2014 by the Society of Nuclear Medicine and Molecular Imaging, Inc.
REFERENCES
- Received for publication August 14, 2013.
- Accepted for publication May 16, 2014.
Jump to section
Related Articles
Cited By...
- The MIRD Schema for Radiopharmaceutical Dosimetry: A Review
- Development and Preclinical Evaluation of [211At]PSAt-3-Ga: An Inhibitor for Targeted {alpha}-Therapy of Prostate Cancer
- [123I]CC1: A PARP-Targeting, Auger Electron-Emitting Radiopharmaceutical for Radionuclide Therapy of Cancer
- Gadolinium-Based Nanoparticles Sensitize Ovarian Peritoneal Carcinomatosis to Targeted Radionuclide Therapy
- Efficacy of HER2-Targeted Intraperitoneal 225Ac {alpha}-Pretargeted Radioimmunotherapy for Small-Volume Ovarian Peritoneal Carcinomatosis
- Marshalling the Potential of Auger Electron Radiopharmaceutical Therapy
- MIRD Pamphlet No. 28, Part 1: MIRDcalc--A Software Tool for Medical Internal Radiation Dosimetry
- Dosimetry in Radiopharmaceutical Therapy
- MIRD Pamphlet No. 27: MIRDcell V3, a Revised Software Tool for Multicellular Dosimetry and Bioeffect Modeling
- Modeling Early Radiation DNA Damage Occurring During 177Lu-DOTATATE Radionuclide Therapy
- Dosimetry for Radiopharmaceutical Therapy: Current Practices and Commercial Resources
- Overview of the First NRG Oncology-National Cancer Institute Workshop on Dosimetry of Systemic Radiopharmaceutical Therapy
- Targeted Brain Tumor Radiotherapy Using an Auger Emitter
- PARP-1-Targeted Auger Emitters Display High-LET Cytotoxic Properties In Vitro but Show Limited Therapeutic Utility in Solid Tumor Models of Human Neuroblastoma
- PARaDIM: A PHITS-Based Monte Carlo Tool for Internal Dosimetry with Tetrahedral Mesh Computational Phantoms
- Targeting Micrometastases: The Effect of Heterogeneous Radionuclide Distribution on Tumor Control Probability
- Antibody with Infinite Affinity for In Vivo Tracking of Genetically Engineered Lymphocytes
- Monte Carlo N-Particle (MCNP) Modeling of the Cellular Dosimetry of 64Cu: Comparison with MIRDcell S Values and Implications for Studies of Its Cytotoxic Effects
- 124I PET Assessment of Response of Bone Metastases to Initial Radioiodine Treatment of Differentiated Thyroid Cancer
- Biokinetic Modeling and Dosimetry for Optimizing Intraperitoneal Radioimmunotherapy of Ovarian Cancer Microtumors
- Comparison of the Therapeutic Response to Treatment with a 177Lu-Labeled Somatostatin Receptor Agonist and Antagonist in Preclinical Models
- Nanoconjugation of PSMA-Targeting Ligands Enhances Perinuclear Localization and Improves Efficacy of Delivered Alpha-Particle Emitters against Tumor Endothelial Analogues
- Monte Carlo Evaluation of Auger Electron-Emitting Theranostic Radionuclides
- Proceedings of the Second NCI-SNMMI Workshop on Targeted Radionuclide Therapy