Abstract
90Y resin and glass microsphere liver radioembolizations delivering lobar doses of 70 and 120 Gy, respectively, display hepatic toxicity similar to 40-Gy fractionated external-beam radiotherapy. We investigated how the lower number of glass microspheres could induce a sufficiently nonuniform dose distribution explaining this paradox. Methods: Microscale dosimetry was assessed in the realistic liver model developed by Gulec et al. but using the Russell’s dose deposition kernel. A lattice of hexagonal prisms represented the hepatic lobules. Two hepatic arterial tree models—that is, a fixed-length and a variable-branches length—were used for the microsphere transport. Equal or asymmetric microsphere relative-spreading probability between 2 daughter vessels was assumed. Several 120-Gy liver simulations were performed: periodic simulations, where 1 or 6 glass microspheres were trapped in all and in only 1 of 6 portal tracts, respectively, and random simulations, where glass microsphere trapping assumed an equal probability for all the portal tracts or a variable probability depending on the successions of artery connections leading to the portal tract, both for the 2 arterial tree models. Results: For the 2 uniform simulations, all hepatic structures received at least 100 Gy. The fast decrease of the 90Y kernel as the inverse of the square of the distance r is counterbalanced by the number of contributing lobules containing microspheres that increases as r2. The random simulation with equal-spreading probability gave for the less irradiated tissue a lobule dose distribution centered around 103 Gy (full width at half maximum, 20 Gy). The distribution became significantly asymmetric with the 60%–40% relative-spreading probability, with a shift of the maximum from 103 down to 50 Gy, and about 17% of the lobules got a dose lower than 40 Gy to their different structures. Conclusion: The large nonuniform trapping produced by the microsphere transport in the arterial tree jointly with the low number of injected glass microspheres begins to explain their lower hepatic toxicity per Gray. In addition, the nonuniform trapping supports the fact that the granular aspect of 90Y PET imaging observed in patients could represent some reality and not only statistical noise.
Recommendations in liver lobar radioembolization are different in terms of maximum-tolerable liver absorbed dose according to the medical device: less than 70 Gy when using resin microspheres (1) and less than 120 Gy with glass microspheres (2). Recent voxel-based dosimetry SPECT/CT studies (3,4) support similar differences in hepatic toxicity risk per Gray for these 2 therapies. For hepatocarcinoma treatment with resin spheres, after a mixed lobar or whole-liver approach, the radiobiologic model described by Strigari et al. (3) reported the value of 52 Gy as the mean liver-tolerable dose for 50% (TD50) risk of toxicity larger than G2 according to CTCAEv4. A similar analysis conducted by Chiesa et al. (4) for the same pathology treated with glass spheres resulted in a TD50 of about 100 Gy for basal Child Pugh A5, though for a different toxicity definition.
According to the formalism of equivalent dose EQD2 (5)—that is, the dose delivered in 2-Gy fractionated external-beam radiotherapy (EBRT) that will provide the same biologic effective dose—100 Gy from irradiation by 90Y corresponds to an EQD2 of 140 Gy. The values of the liver radiosensitivity parameter α/β (2.5 Gy) and of the half-time of sublethal damage repair T1/2 (2.52 h) used to compute EQD2 were extracted from Strigari et al. (3). These values confirm the huge discrepancy with respect to EBRT, where EQD2 values of 45 and 55 Gy for TD50 were observed for two-thirds and one-third liver irradiation, respectively (6). In EBRT, a one-third liver irradiation with an EQD2 of 80 Gy already gives a probability of liver failure higher than 99% (7).
Gulec et al. (8) computed microscale dosimetry using Monte Carlo simulation in a realistic liver model. They assessed the impact of the lower number of glass microspheres per gigabecquerel (≈1.2 × 106/3 GBq), compared with that of resin microspheres (≈6 × 107/3 GBq). They showed that for a periodic microsphere distribution and for the same liver dose of 64 Gy, resin and glass microspheres provided a similar dose to the centrilobular vein (i.e., 59 and 58 Gy, respectively). As a result, when the absorbed dose (64 Gy) modeled by Gulec et al. is rescaled to 100 Gy, all hepatic structures received an EQD2 above 120 Gy—that is, about 3-fold higher using glass microspheres than using resin microspheres or EBRT.
We investigated whether the random nature of microsphere trapping in the portal tracts could induce a nonuniformity in the absorbed dose distribution sufficient to explain the lower hepatic toxicity per Gray of glass microspheres. Two different arterial tree models were investigated: a fixed-length tree model and a randomly grown tree model. The comparison of the dose distribution in the hepatic structures for the different treatments is independent of the liver volume targeted and was performed targeting the whole liver.
MATERIALS AND METHODS
Liver Dosimetry Model
Calculations were performed using the liver model developed by Gulec et al. (8) but with the analytic Russell’s dose distribution kernel (9): Eq. 1where D is the dose in Gy, A the 90Y activity in kBq, and r the radial distance in millimeters.
Eq. 1where D is the dose in Gy, A the 90Y activity in kBq, and r the radial distance in millimeters.
Each hepatic lobule is modeled by a 1.5-mm-length hexagonal prism of a 1.2-mm side-to-opposite-side distance. The portal triads (i.e., portal venule, arterial portal tract, and bile duct) are located at the 6 corners of the hexagon (Fig. 1A) (10). The centrilobular vein is parallel to the portal triads and is located in the hexagon center. Hexagonal lobules are tiled in the 3 directions to form a lattice modeling the liver structure (Fig. 1B).
Gulec et al. (8) simulated a liver dose of 64 Gy corresponding to one 2.5-kBq glass microsphere trapped in every other portal tract. To achieve usable computation time, they assumed all lobules as having identical microsphere trapping; the microscale dosimetry was only assessed for 1 isolated lobule and the cross-firing irradiation from the neighbor lobules was obtained by performing a reflection of the β particles reaching the boundaries of the studied lobule. This speed-up strategy avoids the need of following additional β particles coming from outside the considered lobule. A delivered dose of 120 Gy to the liver corresponds to one 2.34-kBq glass microsphere trapped in every portal tract.
Microsphere Transport Model
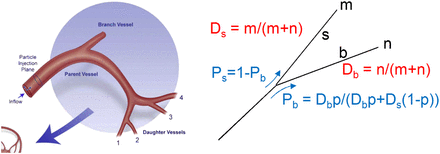
By computer modeling of the steady-state flow, Kennedy et al. (11) derived that in the arterial branch geometry shown in Figure 2 (left), microsphere spreading doesn’t follow that of the blood, and typically 20%, 30%, 30%, and 20% of the microspheres go through daughter vessels 1, 2, 3, and 4, respectively.
(Left) Hepatic arterial system geometry of computational model used by Kennedy et al. where they found typical microsphere local spreading of 20%, 30%, 30%, and 20% in daughter vessels 1, 2, 3, and 4, respectively. (Reprinted with permission of Elsevier (11).) (Right) Relative microsphere-spreading probability used in present model. m and n are number of portal tracts fed by most straight (s) and most bifurcating (b) daughter vessel, respectively. Ds and Db are relative blood flow of vessels constrained to provide same blood flow to each terminal portal tract. Ps and Pb are microsphere relative-spreading probability in vessels for relative blood flow Ds and Db. When Ds = Db, p is probability for microsphere to go into bifurcating vessel. If Ds ≠ Db, this probability is modulated according to different flows.
Resin and glass microspheres significantly differ for the density: 1.6 and 3.6 g/cm3, respectively. However, Basciano (12) showed that the particle density had to be on the order of 10 times greater than the carrier fluid density to noticeably influence microsphere trajectories. Microsphere diameters are similar—that is, 25 and 32 μm for resin and glass microspheres, respectively. This small difference plays a role only approaching the terminal arterioles (13). Thus, the typical glass microsphere relative spreading between daughter vessels 2 (bifurcating) and 1 (straight) is about 60% and 40%, respectively.
Fixed-Length Artery Tree
The hepatic artery is modeled by a tree in which each segment vessel splits into 2 smaller daughter vessels. The liver contains about 106 lobules (8) and 2 × 106 portal tracts (6 portal tracts per lobule but each shared by 3 lobules). For simplicity, we assumed that the total number of portal tracts is 221 = 2,097,152; consequently all the paths had a fixed length of 21 bifurcations (also called nodes). This simplistic model provided a didactic and clear understanding of the different mechanisms.
In this model, the 2 daughter vessels of each node feed the same number of terminal portal tracts and share the same blood flow. An asymmetric microsphere relative-spreading probability was assumed for the 2 daughter vessels of all nodes—that is, at each node one daughter is considered to bifurcate and has a probability p, and the other one is considered to be straight and has a probability 1 − p. The number Npt(n) of portal tracts owning n and Nn − n (0 ≤ n ≤ Nn) daughter vessels with p and 1 − p microsphere relative-spreading probability, along the path going from the catheter tip to the portal tract, is Eq. 2Nn is the number of nodes along the arterial path between the catheter tip and the portal tract (i.e., 21 for a whole-liver radioembolization).
Eq. 2Nn is the number of nodes along the arterial path between the catheter tip and the portal tract (i.e., 21 for a whole-liver radioembolization).
The resulting probability P(n) for a microsphere leaving the catheter to reach this portal tract is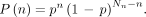 Eq. 3Combinational analysis gives
Eq. 3Combinational analysis gives  —that is, all microspheres will reach a portal tract, and the number of portal tracts targeted is
—that is, all microspheres will reach a portal tract, and the number of portal tracts targeted is  .
.
As a result, the probability Π(ν) that this portal tract trapped ν microspheres when N is the total number of injected microspheres is Eq. 4 A delivered dose of 120 Gy to the whole liver is obtained with
Eq. 4 A delivered dose of 120 Gy to the whole liver is obtained with 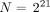 (i.e., the same number of microspheres as the number of portal tracts targeted).
(i.e., the same number of microspheres as the number of portal tracts targeted).
Four 120-Gy whole-liver dose simulations were performed: 2 simulations with periodic microsphere distribution, assuming 1, or 6, glass microspheres trapped in every, or only in 1 of 6, portal tracts, and 2 random simulations using the microsphere transport model with P = 0.5 (i.e., equirelative-spreading probability between 2 daughter vessels) and with P = 0.4 as derived by Kennedy et al. (11).
For each random simulation, 100,000 realizations were performed in a liver subvolume of 16 × 16 × 16 mm, which contained about 211 lobules. All the portal tracts of this subvolume were thus assumed to share a common arterial path of 21 – 11 = 10 nodes length. Each portal tract of this subvolume was randomly populated with microspheres using a probability distribution following Equations 3 and 4 for its individual number n and with Nn = 10. The microscale dose distribution (10-μm voxel size) inside the central lobule of the subvolume was computed using the Russell’s dose kernel (Eq. 1). Lastly, the lobule-distribution histograms versus the different structure dose (i.e., the parenchyma, centrilobular vein, and portal triad of the lobule having the minimal dose) were derived.
Additionally, a 64-Gy liver dose simulation with one glass microsphere trapped in every other portal tract was also performed to validate the present method versus the results obtained by Gulec et al. (8).
Virtual Artery Tree
The 8 artery branches feeding the 8 lobes of the liver were manually drawn. Afterward, the 2 × 106 portal tracts were randomly selected and connected by a new vessel to the closest existing vessel using the constraint that the connection point was closer to the trunk than to the selected portal tract. This constraint avoided retrograde artery vessels that are normally not present in the liver. In addition, the existing vessel was folded during the connection process to minimize the total length of the vessels (Schwen and Preusser (14)). The probability of each portal tract to trap a microsphere leaving the catheter tip was computed by following the artery path from the portal tract to the catheter tip. At each node, the probability was multiplied by Eq. 5for the most bifurcating daughter vessel (b) and multiplied by
Eq. 5for the most bifurcating daughter vessel (b) and multiplied by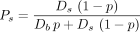 Eq. 6for the most straight daughter vessel (s) (Fig. 2, right). p is the probability for a microsphere to go through the most bifurcating vessel when the blood flows of the 2 daughter vessels are equal. Ds and Db are the relative blood flow of the most straight daughter vessel (s) and of the most bifurcating vessel (b), respectively. These 2 relative blood flows in each node were constrained to ensure an equal individual blood flow to all portal tracts.
Eq. 6for the most straight daughter vessel (s) (Fig. 2, right). p is the probability for a microsphere to go through the most bifurcating vessel when the blood flows of the 2 daughter vessels are equal. Ds and Db are the relative blood flow of the most straight daughter vessel (s) and of the most bifurcating vessel (b), respectively. These 2 relative blood flows in each node were constrained to ensure an equal individual blood flow to all portal tracts.
Lastly, the portal tracts were randomly populated microsphere by microsphere—that is, for each microsphere leaving the catheter, the destination portal tract was randomly selected according to its individual probability to receive a microsphere leaving the catheter tip. The portal tracts have a length of about 1,300 μm (8) and should thus be fully filled after trapping about 50 microspheres. To take into account this physical embolization, after each microsphere deposition in a portal tract, the individual blood flow of this portal tract was reduced, and thus also its trapping probability, to linearly vanish when reaching 50 trapped microspheres. The probabilities of the other portal tracts were rescaled before the next microsphere delivery to conserve a unity total-trapping probability. Several simulations were performed for glass and resin microspheres aiming 120 and 40 Gy to the whole liver, respectively, and with p ranging from 0.3 to 0.7.
RESULTS
Microscale Dosimetry Model
Figure 3 shows that the Russell’s law is in good agreement with the dose kernel computed by Gulec et al. (8), by Cross et al. (15), and by Paxton et al. (16) using different Monte Carlo simulation codes. Paxton et al. (16) in their simulation took into account the actual liver density (1.06 g/cm3) and the glass composition of the microspheres. Both features had a limited impact.
Russell’s law agreement with dose kernel extracted from literature using different Monte Carlo simulation codes. Paxton et al. (16) took into account actual liver density and glass composition of microspheres. Both features have marginal impact.
Periodic Microsphere Trapping
A good agreement was obtained for the hepatic microscale dosimetry computed using the Russell’s law versus the full Monte Carlo dose simulation (Table 1). For 120 Gy to the whole liver, the periodic trapping of 6 microspheres in 1 single portal tract per lobule (C6) does not decrease the doses to the hepatic structures. The last line in Table 1 represents the dose to the centrilobular vein coming only from the microspheres trapped in the portal tracts of this lobule (called nonreflective boundary in Gulec et al. (8)).
Hepatic Microscale Dosimetry in Periodic Trapping
Random Microsphere Trapping
Figure 4 shows the distribution to lobules versus the dose delivered to their different structures obtained for the 4 random simulations. With the equirelative-spreading probability (dashed curves), almost all the lobules received more than 80 Gy to their structures in glass microsphere radioembolization. When the asymmetry of the microsphere relative-spreading probability p between the daughter vessels is considered in the model (solid curves), about 17% and 70% of the lobules have their parenchyma and centrilobular vein receiving less than 40 Gy in glass and in resin microsphere radioembolization delivering 120 and 40 Gy to the liver, respectively. However, for the portal triads the situation is similar for the glass and resin microspheres, where about 25% of the lobules have at least 1 portal triad receiving less than 40 Gy.
Lobule distributions versus dose delivered to their structures for equal microsphere relative-spreading probability between 2 daughter vessels (dashed line) and taking into account asymmetric nature of microsphere transport in nodes of arterial tree (solid line), using fixed-length tree (left graph) and virtual arterial tree model (right graph). Red and pink curves are lobule distribution versus dose to its less irradiated portal triad. Curves are similar for glass- and resin-treatment simulations using asymmetric relative spreading. Centri = centrilobular. D = dose.
Figure 5 shows the distribution of portal tracts, which trapped n microspheres, and the representation of Equations 2 and 3 explaining this distribution.
(A) Solid blue curve: trapping probability using fixed-length tree model for artery paths containing n and 21-n daughter vessels having microsphere spreading of 60% and 40%, respectively. Solid black curve: fraction of portal tracts owning such artery path. Dashed blue line: mean portal tracts trapping probability. Vertical blue line shows that more than half of portal tracts have trapping probability lower than mean probability 1/221. (B) Portal tract distribution versus number of glass microspheres trapped, obtained using fixed-length arterial tree with equal (dark) and asymmetric (light gray) microsphere-spreading probability between 2 daughter vessels and (medium gray) using virtual tree with asymmetric probability.
Figure 6 shows the distribution of lobules having a dose lower than 40 Gy for their different structures obtained using the virtual artery tree model in function of the microsphere relative-spreading probability p. The fraction of lobules having their portal triads receiving a mean absorbed dose of less than 40 Gy in resin microsphere radioembolization delivering 40 Gy to the liver (dashed red curve) is lower than in glass microspheres delivering 120 Gy to the liver (solid red curve). When the physical embolization of the portal tracts by the microspheres was taken into account, glass and resin microspheres displayed a similar distribution for the lobules owning at least 1 portal triad receiving less than 40 Gy (solid and dashed pink curves). This physical embolization significantly affects the resin microspheres but is marginal for the glass ones (data not shown).
Distribution of lobules having dose lower than 40 Gy to their different structures in function of microsphere relative-spreading probability at nodes (i.e., p, Fig. 2). Red curves refer to mean dose of 6 portal triads of lobule. Dotted curve was computed neglecting physical embolization of portal tracts by resin microspheres. Note distribution symmetry versus equal-relative-spreading probability. For 40 Gy to liver using resin microspheres, at least 70% of lobules have their parenchyma and centrilobular vein receiving less than 40 Gy (not shown in graph). When physical embolization process was taken into account, glass and resin microspheres displayed similar distribution of lobules owning at least 1 portal triad receiving dose lower than 40 Gy (solid and dashed pink curves). C. = centrilobular; embol = embolization.
Figure 7 shows the virtual arterial tree and typical time-of-flight (TOF) PET images of 90Y-loaded glass microsphere distribution for a 120-Gy dose to the targeted liver region.
(A) Three-dimensional rendering of virtual arterial tree after generation of first 1,500 vessels. (B and C) Glass microsphere distribution slices aiming 120 Gy to whole liver derived from virtual arterial tree using 50%–50% (B) and 60%–40% (C) microsphere relative-spreading probability between 2 daughter vessels. Slices were convolved with PET spatial resolution. (D) Typical 90Y TOF PET slice not crossing tumor of patient treated with glass microspheres aiming 120 Gy to left liver (6 other patients are shown in supplemental material; supplemental materials are available at http://jnm.snmjournals.org). Random granularity of glass microsphere distribution, such as predicted (C) and observed (D), decreases hepatic toxicity. (E) TOF PET imaging of hot sphere phantom with same acquisition time and same 90Y specific activity as shown in patient image in D.
DISCUSSION
Russell’s Dose Kernel
The Russell’s law is in good agreement with the dose kernel obtained from various Monte Carlo codes (Fig. 3) and provided doses to the hepatic structures similar to those obtained from the full Monte Carlo simulations performed by Gulec et al. (Table 1) (8). The use of Russell’s law has the major benefit to allow the computation of the microscale dosimetry of all the 106 liver lobules that was performed in about 3 h using a Xeon height cores.
Periodic Distribution
Periodically trapping 6 glass microspheres in only 1 portal tract per lobule marginally affected the dose to the hepatic structures, compared with 1 microsphere trapped in every portal tract (Table 1). This might appear improbable considering the fast decrease of the 90Y dose distribution kernel (Fig. 3). In reality, the inverse square decrease as a function of the radial distance r is not fast at all, because the number of contributing lobules containing microspheres and located at this distance r increases with the square of this distance. Only the slow additional linear decrease remains. As a result, the main part of the dose delivered in a point farther than 0.2 mm from any microsphere does not arise from the closest microspheres but arises from the farther microspheres. This feature was already pointed out by Gulec et al. (8) who observed that among the 59 Gy delivered to the centrilobular vein, only 12 Gy arises from the microspheres trapped in the portal tracts of the lobule containing this centrilobular vein (Table 1, last line). The Russell’s law gives a clear explanation of this observation.
Asymmetric Microsphere Relative Spreading
Statistical fluctuations assuming that all portal tracts have the same probability to trap a microsphere leaving the catheter has also a limited impact. This induces only a small spreading of the tissues dose (Fig. 4 dashed lines in left graphic), and almost all the lobules have their structures (i.e., hepatocytes, centrilobular vein, portal triads) receiving a dose higher than 80 Gy (i.e., EQD2 = 98 Gy). This is quite incompatible with the toxicity risk already observed for an EQD2 of 40 Gy in fractionated EBRT.
Assuming that neighbor lobules shared a large part of the fixed-length arterial tree and that the microsphere spreading between 2 daughter vessels is 60%–40% as numerically predicted by Kennedy et al. (11), then the lobule dose distribution becomes significantly asymmetric with a shift of the maximum from 100–110 Gy down to 40–60 Gy (Fig. 4 solid lines in left graphic). As a result, about 17% of the lobules have their structures receiving a dose lower than 40 Gy (EQD2 = 36 Gy), which begins to explain the lower toxicity per Gray using glass microspheres. This shift of the lobule distribution to lower doses results from the shape of the probability function in Equation 3 as shown in Figure 5A (solid blue line): more than half of the portal tracts have a trapping probability lower than the mean probability 1/221. As a result, the 60%–40% microsphere relative-spreading probability increases the fraction of portal tracts without trapped glass microsphere (Fig. 5B). This distribution is in line with the microsphere clustering observed by Kennedy et al. (17) in biopsy.
Although simplistic, the virtual arterial tree took into account the variable number of connection nodes between the catheter tip and the portal tracts and the fact that the difference in arterial paths between neighbor lobules can be sometimes small or sometimes large. These features further shifted the dose distribution a little bit to the left (Fig. 4).
Physical Embolization
The physical embolization of the portal tracts by the resin microspheres had a significant impact: when this physical embolization was neglected, 47% of the lobules had at least a portal triad receiving less than 40 Gy versus 25% when the embolization was taken into account (Fig. 6). Because of the high number of resin microspheres (225 ≈ 3.3 × 107 for 40 Gy to the whole liver), the lobules located on the artery branches owing the smallest numbers of segment with P = 0.4 should trap more than 50 microspheres, which is incompatible with the microspheres and portal tract sizes. The physical embolization redirected a part of the resin microspheres to portal tracts of lower initial trapping probability. This reduces the nonuniformity of the resin microsphere trapping distribution and decreases the number of portal tracts receiving less than 40 Gy (dotted and dashed pink curves in Fig. 6). This physical embolization is marginal for the glass microspheres because of their lower number (221 ≈ 2.1 × 106 for 120 Gy to the whole liver).
Posttherapy 90Y TOF PET
The synthetic arterial tree allowed simulating a typical glass microsphere distribution. Convolved with the spatial resolution of a TOF PET system, the glass microsphere distribution appeared homogeneous and significantly heterogeneous using the 50%–50% and 60%–40% relative-spreading probability, respectively (Figs. 7B and 7C). This last result supports the fact that the significant heterogeneity observed for 90Y-loaded glass microsphere PET imaging in patients could represent some reality and not only statistical noise.
Model Limitations
The 25% of lobules owning at least a portal triad receiving less than 40 Gy for the glass or resin radioembolization is likely not sufficient to explain why the targeted liver volume can recover and does not end up in full necrosis. The virtual arterial tree was built assuming a random vessel generation up to the single lobule level. However, it is likely that for space optimization, the arterial vessels have some deterministic organization in lobule clusters at the end of the arterial branches. This could contribute to an additional increase of the microsphere distribution heterogeneities and thus increase the fraction of lobules receiving less than 40 Gy.
The 60%–40% microsphere spreading was found by Kennedy et al. (11) in the steady-state dynamics for a particular bifurcation geometry. Basciano et al. (13) showed that just following the catheter tip the microsphere spreading can still be more asymmetric between the daughter vessels, depending on the injection time frame versus the blood motion phase. This should still even increase the microsphere nonuniform trapping. This point has to be further investigated to refine the microsphere distribution modeling. It is also interesting to point out that in terms of dose distribution, it does not matter which daughter vessel (i.e., the most straight or the most curved vessel) owns the highest microsphere relative-spreading probability, as shown in Figure 6. The key feature is the succession of asymmetric relative-spreading probability at each node present between the catheter tip and the final lobule.
Another weakness of the present study is the simplistic virtual arterial tree used. During this last decade, several teams developed sophisticated computer models simulating the physiologic growing of the arterial tree (18,19), taking into account fluid turbulence and viscosity and optimizing blood pressure and vessels radii. However, only simulations of the arterial tree feeding up to 10,000 lobule clusters were reported. Implementing such algorithms in the dosimetry model will make sense only if the microsphere transport in the vessel nodes is also modeled in function of the different curvatures of the vessels bifurcation, of the vessels blood flow, and of the vessels radius.
The portal tract embolization was modeled by a simple linear blood flow reduction versus the number of microspheres trapped. Modeling the exact shape of this reduction required the knowledge of the arterial tract diameter, of the arterial tract wall elasticity, and of the number and the positions of the small arterial vessels entering into the hepatic lobule.
CONCLUSION
The present study is a first step in the explanation of the lower hepatic toxicity of glass microspheres per Gray, which appears to arise from the microsphere transport asymmetry in the nodes of the arterial tree jointly with the low number of glass microspheres injected (1 microsphere per portal tract for a 120-Gy dose to the liver). Implementation of the physiologic arterial tree model including a microsphere transportation model depending on the vessel bifurcation angles and sections will further improve the understanding of the microsphere efficacy. This should help to determine the optimal activity per microsphere to reduce the toxicity in the hepatic lobule without reducing too much the efficacy in tumors that own a different vascularization architecture with respect to normal tissue.
DISCLOSURE
The costs of publication of this article were defrayed in part by the payment of page charges. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 USC section 1734. No potential conflict of interest relevant to this article was reported.
Footnotes
Published online Dec. 2, 2013.
- © 2014 by the Society of Nuclear Medicine and Molecular Imaging, Inc.
REFERENCES
- Received for publication May 28, 2013.
- Accepted for publication October 7, 2013.