Abstract
This article presents a revised voxel S values (VSVs) approach for dosimetry in targeted radiotherapy, allowing dose calculation for any voxel size and shape of a given SPECT or PET dataset. This approach represents an update to the methodology presented in MIRD pamphlet no. 17. Methods: VSVs were generated in soft tissue with a fine spatial sampling using the Monte Carlo (MC) code MCNPX for particle emissions of 9 radionuclides: 18F, 90Y, 99mTc, 111In, 123I, 131I, 177Lu, 186Re, and 201Tl. A specific resampling algorithm was developed to compute VSVs for desired voxel dimensions. The dose calculation was performed by convolution via a fast Hartley transform. The fine VSVs were calculated for cubic voxels of 0.5 mm for electrons and 1.0 mm for photons. Validation studies were done for 90Y and 131I VSV sets by comparing the revised VSV approach to direct MC simulations. The first comparison included 20 spheres with different voxel sizes (3.8–7.7 mm) and radii (4–64 voxels) and the second comparison a hepatic tumor with cubic voxels of 3.8 mm. MC simulations were done with MCNPX for both. The third comparison was performed on 2 clinical patients with the 3D-RD (3-Dimensional Radiobiologic Dosimetry) software using the EGSnrc (Electron Gamma Shower National Research Council Canada)-based MC implementation, assuming a homogeneous tissue-density distribution. Results: For the sphere model study, the mean relative difference in the average absorbed dose was 0.20% ± 0.41% for 90Y and −0.36% ± 0.51% for 131I (n = 20). For the hepatic tumor, the difference in the average absorbed dose to tumor was 0.33% for 90Y and −0.61% for 131I and the difference in average absorbed dose to the liver was 0.25% for 90Y and −1.35% for 131I. The comparison with the 3D-RD software showed an average voxel-to-voxel dose ratio between 0.991 and 0.996. The calculation time was below 10 s with the VSV approach and 50 and 15 h with 3D-RD for the 2 clinical patients. Conclusion: This new VSV approach enables the calculation of absorbed dose based on a SPECT or PET cumulated activity map, with good agreement with direct MC methods, in a faster and more clinically compatible manner.
The assessment of the absorbed dose to target and nontarget tissues is a critical step in patient treatment planning within targeted radiotherapy (i.e., molecular radiotherapy, radioimmunotherapy, and selective internal radiotherapy). Two generalized approaches have been applied to patient organ dosimetry in therapeutic nuclear medicine. The more straightforward approach is to estimate the absorbed dose to organs of interest using anatomic phantoms representative of each patient or, at least, an average patient. This method reports the mean organ dose due to self-irradiation from electron and α-particle emissions, self-irradiation from photon emissions within the organ, and cross-irradiation from photons emitted within surrounding organs and tissues:
If tumor doses are required, they are typically approximated as unit density tissue spheres (1), with no accounting of their dose contribution to surrounding tissues or the host or other organs. These techniques are currently implemented in the OLINDA/EXM (2) software using the stylized phantom series of the Oak Ridge National Laboratory (ORNL). With this method, it is also possible to take into account actual values of patient organ masses for the self-dose terms (via methods outlined in MIRD pamphlet no. 11 (3)) and the cross-dose term via the two-thirds power of the mass. The main advantage of this method is its ease of use, but only the average absorbed dose can be estimated. Neither heterogeneities in either tissue composition or radioactivity distribution nor the anatomic geometry of the source and target tissues within the body of the patient is considered.
At the other extreme, voxelized geometries may be used to represent the organs and tumors as tagged voxels of differing activity levels, and Monte Carlo (MC) radiation transport can be used to assess dose at the voxel level. Geometries can be defined from phantoms (Zubal phantom (4), VIP-Man Phantom (5), NCAT phantom (6), and such) or from a regional CT image of the patient (7,8). For an organ of dosimetric interest (high uptake, radiosensitive, tumor burden, and so on), the average absorbed dose may be obtained by tracking energy deposition events within the target organ and assembling a dose-volume histogram (DVH) through computation of the absorbed dose at each (x, y, and z) voxel within the organ:
The first term of Equation 2 gives the average absorbed dose to a voxel (x, y, and z) within the organ of interest due to α-/electron/γ-emissions within that organ, whereas the latter term gives the dose to a voxel (x, y, and z) in the organ of interest due to photon emissions in the patient's surrounding organs or tissues. The advantage of this technique is that it can handle tissue heterogeneities (bone, soft tissue, air, lung, and such) and take into account the patient-specific anatomic geometry of all source and target tissues. However, this approach is time-consuming and computationally demanding. For example, even though the organs of a voxel phantom are represented as an array of individual tissue voxels, one rarely designates each individual voxel as a target region (because of statistical sampling limitations), and instead one averages the dose across a group of voxels or all voxels of a given target organ. Consequently, even though in theory the MC approach can yield a DVH for radiation sources both inside and outside the target organ, this approach is not widely used in clinical centers.
For a given organ of interest, tissue heterogeneities are not generally present. Thus, characterization of dose per organ voxel can be conveniently handled, as described in MIRD pamphlet no. 17 (9), via an image-based map of time-integrated activity in each voxel of the organ, and radionuclide S values developed at the voxel level, with both taking into account the nonuniformity of the activity distribution. Consequently, the first term in Equation 2 can be easily handled in a far more computationally efficient manner through convolution algorithms based on the fast Hartley transform using voxel S values (VSVs) rather than via direct MC radiation transport. The problem lies in the cross-dose term from photons emitted in neighboring organs, where heterogeneous tissue regions might have to be traversed. The thoracic region, with soft tissues, lungs, bones, and air, is the region in which tissue heterogeneity is the most important in the body. Not taking account of these heterogeneities would lead to large errors in a dose calculation, especially those due to the lungs. On the other hand, the abdominal region is mostly constituted of soft tissues, with low differences in density between each type of tissue (liver, spleen, and kidney). In this case, one can assume that not taking into account tissue heterogeneity would not lead to large differences in the dose calculation.
The voxel dimensions of a cumulated activity map based on a SPECT or PET device depends on the field of view of the acquisition and reconstruction matrix. These parameters can vary from one device to another. When using a convolution-based method such as VSV, it is important to allow for the calculation of the dose map at the voxel dimensions of the imaging device, to adapt the method to all the configurations of voxel dimensions in a clinical environment.
This paper presents a revised VSV approach based on VSVs generated at a fine spatial resolution, with a resampling algorithm used to generate VSVs at any user-defined SPECT or PET voxel dimension. VSV sets at fine spatial resolution are also presented for both the electron and the photon components of the emission spectrum for 9 radionuclides of interest in targeted radiotherapy and diagnostic nuclear medicine (18F, 90Y, 99mTc, 111In, 123I, 131I, 177Lu, 186Re, and 201Tl) in a soft-tissue medium. A validation of the method is also presented, in the case of 90Y and 131I, with simulated spheres and a voxel-based liver model with an embedded tumor, for which the average absorbed dose and the tumor DVHs computed by both methods are compared. We further present the results of a comparison in 2 clinical cases with the EGSnrc (Electron Gamma Shower National Research Council Canada) MC implementation of the 3D-RD (3-Dimensional Radiobiologic Dosimetry) (10) software.
MATERIALS AND METHODS
To the aim of providing VSV for any voxel dimensions of the activity map, VSVs were generated at a fine voxel size. These fine-resolution VSV sets (1 per particle type) can then be used to compute VSV at any user-defined voxel dimensions using an appropriate resampling algorithm. For electron emissions, VSV sets were generated using MC simulations, out to a distance for which the secondary electron dose contributions were negligible. The resampling algorithm was applied on the fine VSV set to compute a VSV set at the resolution of the PET or SPECT activity map. For photon emissions, the fine-resolution VSV sets were generated by MC simulations, out to a source-to-target distance for which the angular dependence becomes negligible for the VSV. Beyond this distance, the voxels can be considered as point targets to the voxel source. VSVs are then calculated by the point kernel (PK) approach (11). The photon sets, calculated by MC, are combined with VSVs calculated by the PK approach and resampled at the activity map voxel dimensions. The resampled VSV sets coming from electron and photon contributions are added to form a new set of VSVs for each radionuclide for dose assessments in either therapeutic or diagnostic nuclear medicine in a clinically compatible manner. The description of the development of the fine-resolution VSV approach is given in Figure 1.
Flow chart of development of fine-resolution VSV approach.
Calculation of VSV at Fine Resolution
VSVs at fine resolution were generated using the MC radiation transport code MCNPX (ORNL), using the mesh tally card. The rectangular mesh tally is used to compute the absorbed dose to each voxel by building a regularly spaced mesh. The source is defined as a voxel, in which the particle emission location and emission angle are randomly sampled. Particles are tracked in the targeted material (reported at 1.04 g·cm−3 by the International Commission on Radiation Units and Measurements [ICRU] (12)), and the deposited energy is recorded in each voxel defined by rectangular mesh tally, using the type-3 tally. The average absorbed dose per simulated particle is calculated in MeV·cm−3 and then converted to mGy·MBq−1·s−1 to be used as a VSV kernel. For electron transport, the Integrated TIGER Series mode, which provides better energy binning than the MCNP default mode, is used (13), and an electron cutoff energy of 10 keV is applied. VSVs were generated for 9 radionuclides: 18F, 90Y, 99mTc, 111In, 123I, 131I, 177Lu, 186Re, and 201Tl. The radionuclide decay schemes used were those published by Eckerman and Endo (14).
To obtain a compromise between the calculation time and absorbed dose accuracy, several computational characteristics were chosen and assumptions were made. Given the fact that photons are more penetrating than electrons, a different voxel size was chosen for electron and photon emissions. For electrons, the fine-resolution VSV matrix was set to 0.5 mm, whereas for photons it was set to 1 mm. To limit the size of the electron VSV set, we assumed that bremsstrahlung photons make negligible contributions to the dose matrix. The VSV kernels are then generated for an array size up to the continuous slowing down approximation range of the most energetic electron particle in the decay scheme for each radionuclide.
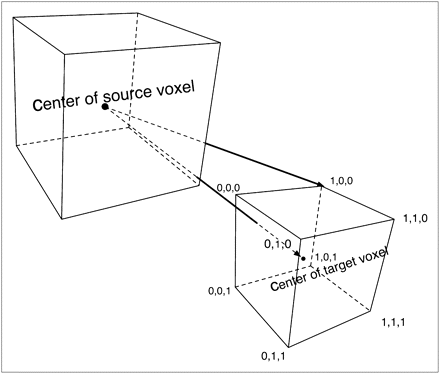
For photons, VSVs were calculated with the direct MC approach, out to a distance for which the angular dependence of VSV becomes negligible. To evaluate the distance above which this assumption can be made, the source-to-target voxel distance has been calculated for the 8 corners of the voxels and compared with their center-to-center distance, as shown in Figure 2. This distance was chosen to be a voxel index of 10—that is, a distance equal to 10 voxel lengths—because the maximum error on the distance made by this assumption is 10%. Given i, j, and k, the coordinates of an individual voxel within the array, the voxel index is defined as
Representation of difference in distance to source when target point is considered to be at center or at random point within voxel. Coordinates shown are those of vertices.
VSVs were calculated, with sufficient histories to ensure a mean relative error below 1% within the fine-resolution matrices. For electrons, this criterion required 109 particle histories, whereas 108 histories were required for the photon component of the emission spectrum.
Resampling Procedure
The resampling procedure is explained for cubic voxels. We define δxyz as the isotropic resolution of the fine-mesh VSV matrix (VSV∂xyz) and Δxyz as the desired VSV matrix resolution (VSVΔxyz) given by the SPECT or PET system. To perform the appropriate resampling, one must consider that for each user-defined voxel size Δxyz, the radiation source has to be expanded to achieve the size of the targeted voxel. The source of the targeted voxel size is then simulated by considering that the source of VSVΔxyz contains (Δxyz/δxyz)3 sources of VSVδxyz. Once the voxel source is created, the VSVδxyz is resampled by grouping and averaging the fine-resolution voxel results.
For voxel sizes that cannot be obtained by resampling of the fine VSV matrix using the averaging method, an interpolation model (inverse second order) is applied between the 2 nearest voxel sizes (Δxyz) that can be obtained without interpolation. As an example, for a voxel size of 4.8 mm, the interpolation is performed using voxel matrices of 4.5 and 5.0 mm.
Dose Calculations Using VSVs
After the resampling step, the VSVs are generated at the appropriate voxel size. These VSVs can thus be used for dose calculation following the MIRD schema (15), for which the dose to a target tissue region rT is the result of the contributions of itself and all surrounding source tissue regions rS:
When using VSVs, the target and sources are voxels from the patient's cumulated activity map, acquired with a SPECT or PET detector array, for which the size and shape of the voxels are defined by the field of view of the acquisition matrix and the reconstruction matrix. For a given target voxel (voxelT), its average absorbed dose is calculated as the summed contribution from all N voxels (voxelS), with each contribution given as the product of time-integrated activity and the voxel-to-voxel S value:
Equation 4 is implemented as a discrete convolution using a fast Hartley transform. The VSV matrix, computed for given radionuclide and voxel dimensions, is used as a kernel to convolve the cumulated activity map and obtain the average absorbed dose for each voxel of the cumulated activity map.
Validation Studies
Validation studies were conducted for 90Y and 131I by comparing absorbed doses computed by the VSV approach and direct MC simulation, using MCNPX for a voxelized geometry at the cumulated activity map resolution. These validation studies were performed on simulated spheres of various radii for several cubic voxel sizes and for a clinical case, also simulated, for a single voxel size. Comparisons were performed on the average absorbed dose as well as the resulting DVH; these last were estimated by calculating the relative difference between DVH integrals.
In this comparison, we performed the MC simulations using MCNPX with lattice geometry to simulate the voxelized geometries. The Tally Card F6 was used for electrons, for which the energy deposition can be considered to be locally deposited, and the absorbed dose was obtained in MeV·g−1 and converted to units of Gy. For photons, the *F8 tally was more appropriate because of potential secondary electrons that are not tracked in the F6 tally (16,17). The absorbed dose was obtained in megaelectron volts and converted to grays.
The spheric tissue phantoms corresponded to 20 soft-tissue (composition at 1.04 g·cm−3 according to a report by the ICRU (12)) spheres uniformly filled with activity, with 5 different radii (4, 8, 16, 32, and 64 pixels) and 4 voxel (cubic) sizes (3.8, 4.8, 5.3, and 7.7 mm). The spheres were presumed to be surrounded by a soft-tissue region void of additional radioactivity. For all spheres, we fixed the cumulated activity in each voxel at 100 Bq-s. The number of simulated histories was 106 for each sphere.
A voxelized liver was then used for a more advanced comparison between the VSV approach and direct MC approach. The liver was manually segmented within a CT scan from a patient, and a 3.42-cm-diameter sphere was included, simulating a hepatic tumor. The original CT scan resolution was 0.79 × 0.79 mm in-plane and had a slice thickness of 3.75 mm. The image was resampled to a more common spatial resolution for nuclear medicine applications: 3.80 × 3.80 × 3.80 mm, as shown in Figure 3. The activity was assumed to be uniformly distributed within the liver and tumor but at different activity levels, and each was modeled as soft tissue according to the definition provided by the ICRU (12). As with the tissue spheres, the liver was presumed to be surrounded by soft tissue containing no additional radioactivity. The time-integrated activity was set to 10 Bq-s per voxel for the nontumor regions of the liver (28,231 voxels), and 100 Bq-s per voxel for the tumor (257 voxels), corresponding to 282 kBq-s and 25.7 kBq-s, respectively, for the 2 volumes. Two simulations were performed for 90Y and 131I for the DVH comparison, with several histories of 1010 simulated for both radionuclides.
Voxelized liver with tumor included; resolution was 3.8 × 3.8 × 3.8 mm.
Comparison with 3D-RD Software Using EGSnrc-Based MC on 2 Targeted Radiotherapy Patients
The fine VSV approach was compared with the 3D-RD software, using an EGSnrc-based MC calculation on 2 targeted-radiotherapy patients. Computations were performed assuming a homogeneous distribution of radioactivity in soft tissues and a density of 1.04 g cm−3 (12). The 3D-RD calculations were done with 108 histories.
90Y-Ibritumomab Tiuxetan Radioimmunotherapy
The first patient had non-Hodgkin lymphoma treated by 90Y-ibritumomab tiuxetan radioimmunotherapy. The time-integrated activity map was derived from 111In SPECT quantitive images at 5 time points and a monoexponential time–activity curve (18) for the liver, spleen, and kidneys. The dose calculation was performed on a 93 × 62 × 64 matrix—that is, for 369,024 voxels.
131I-Lipiodol Selective Internal Radiotherapy
The second patient corresponded to a phantom comprising a liver and tumor with 131I-lipiodol distribution. The cumulated activity map was derived from the study of Raoul et al. (19). The dose calculation was performed on a 53 × 54 × 36 matrix—that is, 103,032 voxels. For both patients, the average absorbed dose and dose distribution (voxel to voxel) were compared between VSV and 3D-RD calculations.
RESULTS
The fine-resolution VSV sets are shown in Supplemental Figures 1–3 (supplemental materials are available online only at http://jnm.snmjournals.org). The MCNP input codes (as might be needed to generate fine-resolution VSV sets for other radionuclides) are additionally provided in the Supplemental Appendix.
Sphere Models
For the various tissue sphere phantoms, Table 1 shows that the relative difference between the new VSV approach and direct MC calculation is 0.20% ± 0.41% for 90Y (n = 20 spheres). For 131I, the relative difference is 0.22% ± 0.19% for the electron component of the emission spectrum, and −1.38% ± 0.69% for the photon component. The overall relative difference is −0.36% ± 0.51% for 131I. The results show no evidence of a relationship between the size of the object and percentage difference between the VSV approach and direct MC approach.
Relative Differences Between VSV and Direct MC Approaches for 90Y and 131I on 20 Spheres
For the tissue sphere phantoms, the calculation time on a desktop computer running Windows XP (Microsoft), with a 2.99-GHz Intel Pentium 4 central processing unit (CPU) and 1 GB of RAM, was less than 10 s for VSV (resampling) and dose (convolution) calculations. For a direct MC simulation using MCNPX, the time to compute the average absorbed dose ranged from 10 to 17 min on the same configuration, depending on the sphere size.
Liver and Tumor Phantom
Comparisons of Average Absorbed Dose.
For the hepatic tumor phantom, with cubic voxels of 3.8 mm, the relative difference in average absorbed dose between VSV and direct MC was −0.33% for the tumor and 0.25% for the liver parenchyma in the case of 90Y and −0.15% for the tumor and −0.16% for the liver parenchyma in the case of 131I. The calculation time on a desktop computer with the same parameters as for the sphere model was below 10 s for VSV (resampling) and dose (convolution) calculations but greater than 10 min for the MC simulation using MCNPX.
DVH Comparison for Tumor.
Figures 4A and 4B show the DVH difference between VSV and direct MC (1010 histories) for 90Y and 131I, respectively. These figures show modest differences between the 2 methods. The absolute relative differences between the VSV and direct MC DVH integrals are 1.26% for 90Y and −3.26% for 131I. The calculation time on a desktop computer with the same parameters as for the sphere model was around 10 s for VSV (resampling) and dose (convolution) calculations. The calculations with MCNPX took approximately 1 mo for each radionuclide to achieve 1010 histories across the whole organ volume using 5 AMD dual 1.6-GHz CPUs.
(A) Comparison between VSV and direct MC methods for DVH obtained for simulated hepatic tumor for 90Y. (B) Comparison between VSV and direct MC methods for DVH obtained for simulated hepatic tumor for 131I.
Comparison with MC-Based Software Used for 2 Targeted-Radiotherapy Cases
90Y-Ibritumomab Tiuxetan Radioimmunotherapy.
Figure 5A shows 2-dimensional dose distributions on a transverse slice, calculated by VSV and 3D-RD 108 histories. Table 2 compares the average doses calculated for the regions of interest (ROIs). The relative difference between VSV and 3D-RD ranges from 0.09% to 0.25%. The modal value of the voxel-to-voxel ratio ranges from 0.995 (SD = 0.023) to 0.996 (SD = 0.027). The calculation time on a desktop computer with the same parameters as for the sphere model was 3 s for VSV (resampling) and dose (convolution) calculations. The calculation time with 3D-RD was 50 h (108 histories) on an 800-GHz Intel Xeon CPU.
(A) Dose map comparison on given transverse slice for 90Y-ibritumomab tiuxetan patient. VSV is compared with 3D-RD calculations done with 108 histories. (B) Dose map comparison on given transverse slice for 131I-lipiodol patient. VSV is compared with 3D-RD calculations done with 108 histories for β-particles and photons.
90Y-Ibritumomab Tiuxetan Patient: Cumulated Activity, Organ Mass, Dose Calculated by VSV and 3D-RD, and Relative Differences for Corresponding ROIs
131I-Lipiodol Selective Internal Radiotherapy.
Figure 5B shows 2-dimensional dose distributions on a transverse slice, calculated by VSV and 3D-RD. Table 3 compares the average doses calculated for the ROIs. The relative difference between VSV and 3D-RD is 0.94% for the liver and 0.67% for the tumor (108 histories). The modal value of the voxel-to-voxel ratio is 0.994 (SD = 0.017) for the liver and 0.991 (SD = 0.008) for the tumor.
131I-Lipiodol Patient: Cumulated Activity, Organ Mass, Dose Calculated by VSV and 3D-RD, and Relative Differences for Corresponding ROIs
The calculation time on a desktop computer with a 2.99-GHz Intel Pentium4 CPU was 5 s for VSV (resampling) and dose (convolution) calculations. The calculation time with 3D-RD was 15 h (108 histories) on two 800-GHz Intel Xeon CPUs.
DISCUSSION
MIRD pamphlet no. 17 provided the technical basis for extending the MIRD schema to applications involving direct quantification of radionuclide activity in both PET and SPECT (20). Representative sets of radionuclide VSVs were provided for 5 radionuclides (32P, 89Sr, 90Y, 99mTc, and 131I) at 2 voxel sizes (3 and 6 mm) representative of PET and SPECT, respectively. One additional set at a voxel size of 0.1 mm was provided for 131I for applications to autoradiography. In many instances, however, nuclear medicine images are acquired in noncubic voxels over a wide range of matrix sizes and fields of view, and thus, there is a need for a more real-time method to generate VSV sets at user-defined dimensions.
In this study, a revised approach is presented to yield VSV matrices with greater accuracy and user flexibility. To this aim, the radionuclide decay scheme was integrated in the VSV generation, VSV sets were computed at a fine spatial resolution using MC simulations, and then VSV sets were resampled to adjust to the clinical acquisition conditions. These fine-resolution VSV sets were generated for 9 common radionuclides used in nuclear medicine, in a soft-tissue medium, and for a fine sampling of 0.5 mm for electrons and 1 mm for photons. Nevertheless, it is possible to obtain additional sets for other radionuclide emission spectra and fine sampling by adapting the MCNPX code provided in the Supplemental Appendix. The resampling algorithm would be applied the same way as for the sets provided here, and if one generates VSV at a finer resolution, the resulting dosimetry accuracy would obviously be improved.
The methodology has been validated for 90Y and 131I, through comparisons with the direct MC transport simulation, for 20 tissue spheres uniformly filled and an anthropomorphic phantom consisting of a liver and tumor uniformly filled with different activity concentrations. The average absorbed dose was compared in both cases, and the mean differences between the VSV approach and the direct MC were less than 1%. These results show that the assumptions and choices made in the construction of the VSV fine-resolution sets, and the resampling algorithm and interpolation model (inverse second order), are appropriate.
One of the advantages of the VSV approach is that the computation time is not related to the heterogeneity of the activity distribution within the source. If the source is highly heterogeneous, the convolution will be performed exactly the same way as it would be for a homogeneous distribution. This is not true for direct MC simulations, for which one cannot accurately define a heterogeneous activity distribution without defining as many sources as there are source voxels present in the activity map. This then leads to greater required computation time for the latter approach.
Additionally, if one wants to compute DVHs, the VSV approach allows one to have low statistical errors at the voxel level practically unachievable at present for MC simulations within a reasonable computation time and without invoking high-performance parallel-architecture simulation techniques. As an example, the VSV sets were generated with 109 particles. The equivalent MC simulation to achieve the same statistical precision in the case of our hepatic tumor model (28,231 voxels) would require a simulation of 2.85 × 1013 particles. However, the comparison between tumor DVHs calculated from VSV dose and direct MC dose maps from a 1010-history simulation showed that the 2 approaches agreed well (relative difference between the DVH integrals of 1.26% for 90Y and −3.26% for 131I).
A comparison of the VSV approach with the well-established software 3D-RD, which used the EGSnrc-based MC implementation for these calculations, showed that the 2 methods agreed well for an estimation of the average absorbed dose for an MC computation with a high number of histories (1,000 per voxel). The voxel-to-voxel comparison showed good agreement between VSV and 3D-RD; however, the computation time for 3D-RD was greater than 10 h (15 for 131I and 50 for 90Y). A low number of histories (10/voxel) would induce a lower computation time (by a ratio of 100) but greater discrepancies on a voxel-to-voxel comparison due to statistical fluctuations. Nevertheless, the average absorbed doses within ROIs would remain acceptable.
The disadvantage of the VSV approach is that it does not take into account tissue heterogeneities; however, one can assume that these heterogeneities do not induce significant errors for the dose calculation within the host organ or tissue ROIs, that is, the self-dose. For the cross-dose calculation, we suggest that a study of the impact of tissue heterogeneities should be undertaken before one approach or the other is applied. Previous work has shown that the sensitivity to tissue heterogeneity will depend on the heterogeneity and also the emission spectrum of the radionuclide (21), although in many cases the direct MC approach will be inevitable.
Both approaches can be associated. When tissue heterogeneities cannot be neglected in the cross-dose calculation and the self-dose can be calculated in a homogeneous medium (this assumption can be valid in numerous cases), then the VSV and the direct MC approaches can be associated to compute a dose map, each approach being a complement to the other. Equation 2 would then become:
This new VSV approach enables computation of the self-absorbed dose with accuracy close to that achievable with direct MC simulation. Accordingly, it can be easily integrated into clinical practice without the need for high-end computational platforms.
CONCLUSION
The VSV approach is a compromise between simplified phantom-based models and the more advanced uses of direct MC simulations, allowing one to achieve better dose distribution information in the clinical environment. For the clinical examples presented, the order of magnitude of the computation time ratio was 10,000 (108 histories) for an MC simulation giving an equivalent dose distribution in term of statistical fluctuation.
The use of a fine-mesh VSV data array, along with an interpolation for user-specified image voxel dimensions, can lead to a rapid yet accurate method for assessment of nonuniform distributions of radiopharmaceutical activity in anatomic regions in which tissue heterogeneities are minimal or nonexistent.
Acknowledgments
We thank the RSICC (Radiation Safety Information Computational Center), at the ORNL, for providing us with additional computer resources for our example calculations. This work was supported by the French League Against Cancer and by NIH grant R01 CA116477.
- © 2010 by Society of Nuclear Medicine
REFERENCES
- Received for publication March 16, 2010.
- Accepted for publication June 25, 2010.