Abstract
This paper presents a systematic analysis of the inherent uncertainty in internal dose calculations for radiopharmaceuticals. A generic equation for internal dose is presented, and the uncertainty in each of the individual terms is analyzed, with the relative uncertainty of all terms compared. The combined uncertainties in most radiopharmaceutical dose estimates will be typically at least a factor of 2 and may be considerably greater. In therapy applications, if patient-individualized absorbed doses are calculated, with attention being paid to accurate data gathering and analysis and measurement of individual organ volumes, many of the model-based uncertainties can be removed, and the total uncertainty in an individual dose estimate can be reduced to a value of perhaps ±10%–20%. Radiation dose estimates for different diagnostic radiopharmaceuticals should be appreciated and considered, but small differences in dose estimates between radiopharmaceuticals should not be given too much importance when one is choosing radiopharmaceuticals for general clinical use. Diagnostic accuracy, ease of use, image quality, patient comfort, and other similar factors should predominate in the evaluation, with radiation dose being another issue considered while balancing risks and benefits appropriately.
- radiobiology/dosimetry
- radiopharmaceuticals
- radiation safety
- internal dose assessment
- radiopharmaceuticals
- uncertainty
Radiation dose estimates for radiopharmaceuticals are widely reported by different groups and individuals, using various modeling assumptions and computational techniques. The reported estimates are mean or median values for large populations of individuals and are sometimes reported with uncertainty estimates but usually as observed standard deviations (SD) and coefficients of variation for the group of subjects studied. In this paper, a systematic analysis of the inherent uncertainty in internal dose calculations for radiopharmaceuticals is presented. Each term of the dose equation is evaluated for its individual uncertainty, and an overall uncertainty is then evaluated (although not calculated analytically via classic error propagation, for reasons that will be explained).
To evaluate the overall uncertainty in a radiation dose estimate, one must consider the uncertainty in each of the contributing terms. (Note that the generic word dose in this article may refer to a number of dose quantities, such as absorbed dose, equivalent dose, or effective dose. Most of the analysis in this paper regards the mean dose to whole organs—currently the most widely used quantity in internal dose analysis. Later, some brief discussion of the uncertainty in dose calculations at the tissue or cell level is provided, but a systematic analysis of uncertainty in these applications is not treated.) A generic equation for the average absorbed dose in a target region T (e.g., an organ or tissue with radiopharmaceutical uptake) may be shown as: Eq. 1where DT is mean absorbed dose (Gy or rad) to a target region of interest; ÃS is the time–activity integral of the activity within the source region (Bq s) or (μCi h); yi is the number of radiations with energy Ei emitted from the radionuclide per nuclear transition ([Bq s]−1 or [μCi h]−1); Ei is the mean energy of the ith radiation (MeV); ϕi is the fraction of energy emitted for the ith radiation in a source region that is absorbed in the target region, also sometimes called absorbed fraction; mT is the mass of the target region (kg or g); and k is the proportionality constant (Gy kg Bq−1 s−1 MeV−1 or rad g μCi−1 h−1 MeV−1).
Eq. 1where DT is mean absorbed dose (Gy or rad) to a target region of interest; ÃS is the time–activity integral of the activity within the source region (Bq s) or (μCi h); yi is the number of radiations with energy Ei emitted from the radionuclide per nuclear transition ([Bq s]−1 or [μCi h]−1); Ei is the mean energy of the ith radiation (MeV); ϕi is the fraction of energy emitted for the ith radiation in a source region that is absorbed in the target region, also sometimes called absorbed fraction; mT is the mass of the target region (kg or g); and k is the proportionality constant (Gy kg Bq−1 s−1 MeV−1 or rad g μCi−1 h−1 MeV−1).
The quantity ÃS (sometimes called cumulated activity) represents the integral of AS(t), the time-dependent activity within the source region: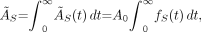 Eq. 2where A0 is the activity administered to the patient at time t = 0, and fS(t) may be called the fractional distribution function for a source region (i.e., the fraction of administered activity present within the source region at time t). In many instances, the function fS(t) may be modeled as a sum of exponential functions:
Eq. 2where A0 is the activity administered to the patient at time t = 0, and fS(t) may be called the fractional distribution function for a source region (i.e., the fraction of administered activity present within the source region at time t). In many instances, the function fS(t) may be modeled as a sum of exponential functions: Eq. 3where the terms f1…fN represent the fractional uptake of the administered activity within the first to Nth components of the source region, λ1…λN represent the biologic elimination constants for these same components, and λP represents the physical decay constant for the radionuclide of interest. Other functional expressions may be used to represent the fractional distribution function, but exponentials are most commonly encountered.
Eq. 3where the terms f1…fN represent the fractional uptake of the administered activity within the first to Nth components of the source region, λ1…λN represent the biologic elimination constants for these same components, and λP represents the physical decay constant for the radionuclide of interest. Other functional expressions may be used to represent the fractional distribution function, but exponentials are most commonly encountered.
A generalized expression for calculating internal dose, which may describe the equations shown in publications by different authors, is given by the following equation: Eq. 4where N is the number of nuclear transformations that occur in source region S (identical to ÃS), and DF is a dose factor. The factor DF contains the various components shown in the formula above for dose other than cumulated activity, namely the decay data and absorbed fractions (ϕ's), which are derived generally using Monte Carlo simulation of radiation transport in models of the body and its internal structures (organs, tumors, etc.):
Eq. 4where N is the number of nuclear transformations that occur in source region S (identical to ÃS), and DF is a dose factor. The factor DF contains the various components shown in the formula above for dose other than cumulated activity, namely the decay data and absorbed fractions (ϕ's), which are derived generally using Monte Carlo simulation of radiation transport in models of the body and its internal structures (organs, tumors, etc.): Eq. 5
Eq. 5
As written, the above equations give only the dose from 1 source region (S) to 1 target region (T), but they can be generalized easily to multiple source regions: Eq. 6
Eq. 6
Let us take the terms in Equation 6 one by one and evaluate the relative uncertainty of each. We will discuss the terms in order of increasing uncertainty.
CONVERSION FACTOR, K
The factor k has zero uncertainty. It is an analytic quantity based on known conversion constants. The proportionality constant k includes the various factors that are needed to obtain the dose in the desired units, from the units used for the other variables, and it is essential that this factor is properly calculated and applied. For example, if we want the dose rate in rad/h, and we have used units of μCi for activity, MeV for energy, and g for mass, the conversions that are needed are: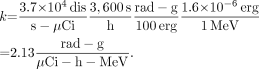 Eq. 7
Eq. 7
If instead we want the dose rate in mGy/s, and we have used units of MBq for activity, MeV for energy, and kg for mass, the conversions that are needed are: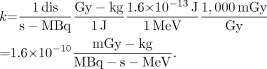 Eq. 8
Eq. 8
DECAY DATA TERMS, YI AND EI
The uncertainty in the terms yi and Ei is low and mostly negligible, in comparison with uncertainties in the other terms, which we will discuss next. For some low-energy and low-abundance emissions (e.g., Auger electrons), the uncertainty may be considerable but will generally not be important to final estimates of calculated dose for an organ, when all errors are included. Table 1 shows decay data for 99mTc, as taken from the Brookhaven National Laboratory National Nuclear Data Center decay data compendium. The values in italics to the right of any number (if given) provide 1 SD of uncertainty for the rightmost digits of a given number. For example, the last 2 numbers in the first row are 0.447% ± 0.011% and 1.08E−05 ± 3E−7.
Photon Component of Decay Data for 99mTc
PHYSICAL MODEL–RELATED TERMS, ϕ AND M
The other 3 terms in the equation, namely ϕ (or absorbed fraction), N (or ÃS), and mT, contribute most of the uncertainty to an internal dose calculation. The absorbed fraction and mass terms used in most internal dose calculations are based on standardized individuals, that is, reference man, reference woman, reference pediatric individuals, and so on. The anthropomorphic models, or phantoms, that have been derived to represent these standard individuals, when used in these calculations, provide doses to the supposedly median individual in a reference group. Nuclear medicine patients vary substantially in body size and shape, and the dose estimates for these standard individuals are accurate for only a small percentage of the individuals encountered in actual practice. The currently available anthropomorphic models are stylized and incorporate mathematic-equation–based descriptions of organ and body surfaces (Fig. 1, left) (1). Although more realistic models will soon replace these stylized models (e.g., Fig. 1, right) (2), these models, as well, were designed to represent the median individual in a population, and application to a given individual, or even the subpopulation of nuclear medicine patients, may result in considerable uncertainty in the numeric values of dose estimated for a given organ for a given radiopharmaceutical.
Stylized anthropomorphic model representing adult male/female of Cristy/Eckerman phantom series and newer, realistic anthropomorphic model representing adult male.
The most recently recommended reference masses for organs of adults and children of various ages, used in designing these reference models, are given in Table 2 (3). Much literature research and investigation has gone into the choosing of these reference values, and they are quite trustworthy as median values for a general population. But variations for individuals or specific subpopulations must be appreciated. The OLINDA/EXM computer code (4) does allow for a first-order scaling of standard phantom organ doses for individual-subject organ mass, if this is known (e.g., from CT volumetrics). Such adjustments are typically applied only in therapy situations, however. The model shown in the right-hand part of Figure 1 was designed using nonuniform rational B-spline surfaces (5), is easily scalable, and so can be modified to model individual patients if desired. Such efforts are reasonable to expend in therapy applications but are not likely to be used routinely in diagnostic situations.
Reference Masses for Organs of Adults
When standardized phantoms are used with Monte Carlo radiation transport simulation codes to obtain absorbed fraction values (or specific absorbed fractions [SAFs], which are equal to the absorbed fraction divided by the mass of the target region), the absolute uncertainty in the calculated absorbed fractions or SAFs can be limited (to ∼5% or less) simply by performing a large number of radiation transport histories. Thus, the inherent uncertainty is small and somewhat comparable to that for the decay data. However, the error caused by application of these SAFs and organ mass values to individuals who are not well represented by the population median value will thus be as much as the individual's body geometry varies from the median. Table 3 shows the variability of organ mass for several organs in men, as reported by de la Grandmaison et al. (6).
Reported Variability of Organ Mass for Several Organs in Men, According to Subject Height
In a presentation to the Society of Nuclear Medicine in 2007, Gesner et al. (7) reported data from a study involving the scaling of a phantom representing the median (50th percentile) individual to individuals of the 10th, 25th, 75th, and 90th percentiles. Their preliminary data suggested that absorbed fractions for many organs vary by about 0.5%–1.0% per kilogram change in total body mass (Fig. 2) (7), although actual deviations of photon-absorbed fractions from those of the median individuals depended on the photon energy. This group is performing a systematic study of how SAFs vary with changes in body size, both in normal-weight and in obese individuals, across the adult and pediatric populations and will soon have more results. These results can finally provide some understanding of the true variability of the SAFs across the nuclear medicine population.
Variations in photon specific absorbed fractions for different-sized individuals illustrated using liver and lung as source and target regions, respectively, near median individual size (57 kg).
BIOKINETIC PARAMETERS, N (OR ÃS)
The function representing the uptake and clearance of radiopharmaceuticals is usually modeled as a sum of exponential functions, including terms representing the fractional uptake of the administered activity for different components of the source region (f1…fN), terms representing the biologic elimination constants for these same compartments (λ1…λN), and the physical decay constant for the radionuclide of interest (λP). This last term has low uncertainty, comparable to that for other decay data. The terms fi and λi are fitted parameters, usually derived from a computer program that performs a regression of the complete retention function against observed data. The complete function, Eq. 9will then be integrated to obtain the cumulated activity (number of disintegrations in source region S) ÃS:
Eq. 9will then be integrated to obtain the cumulated activity (number of disintegrations in source region S) ÃS: Eq. 10and thus the uncertainties in each term will be propagated. However, although the uncertainty in the fitted parameters for the individual retention functions is appreciable, what is more often characterized is simply the empirically observed variability in values of ÃS when data are observed in a given number of individuals studied to determine the kinetics of a given radiopharmaceutical. Standardized dose estimates for diagnostic pharmaceuticals are based on the mean or median kinetics of a small group of animal or human subjects. In therapy situations, kinetics may be established for each individual, with tailored dosimetry performed, perhaps even with scaling of doses to account for known individual organ masses, if available.
Eq. 10and thus the uncertainties in each term will be propagated. However, although the uncertainty in the fitted parameters for the individual retention functions is appreciable, what is more often characterized is simply the empirically observed variability in values of ÃS when data are observed in a given number of individuals studied to determine the kinetics of a given radiopharmaceutical. Standardized dose estimates for diagnostic pharmaceuticals are based on the mean or median kinetics of a small group of animal or human subjects. In therapy situations, kinetics may be established for each individual, with tailored dosimetry performed, perhaps even with scaling of doses to account for known individual organ masses, if available.
The first step in fitting biokinetic data is simply the data acquisition. Siegel et al. (8) discuss some of the strengths and limitations of the various data-gathering methods available in this discipline. Influences on the quality of the data include inherent system limitations on energy resolution, then degradation of spatial resolution because of collimator septal penetration by high-energy photons (if present in the decay scheme), data loss due to scatter and attenuation, and of course the inherent statistical variability in any measurement of a radioactive source. The magnitude of quantification errors has been reported by several authors for planar (conjugate view) imaging as being a few percentage points for large objects to tens or hundreds of percentage points for small objects with low source-to-background contrast (9–14). Generally better results, with perhaps 10%–30% uncertainty for objects of various sizes, have been reported with the use of high-quality SPECT quantitative imaging (11,15–17). Uncertainties in individual data points, however, are not always used in the fitting of the data in a regression or compartment model; often only the scatter of the data is included in reported uncertainties in the fitted parameters from a kinetic analysis. When standardized biokinetics are used, considerable variability may be seen across the group of subjects; however, this information is rarely documented and presented for diagnostic studies for individual radiopharmaceuticals. An example of the observed variability in radiopharmaceutical biokinetics was given by Breitz et al. (18) for the urinary excretion of 166Ho-1,4,7,10-tetraazacyclododecane-1,4,7,10-tetramethylene-phosphonate in 12 subjects with multiple myeloma (Fig. 3). Other authors have pointed out that the uptake and retention of radiopharmaceuticals may vary substantially between patients (8). Most biokinetic models do not take into account disease states, functional organ impairment, the influence of other medications, or other influences that can substantially alter biokinetics, although the literature includes a few examples treating of this (e.g., the 1975 report by Cloutier et al. on the dosimetry of 198Au colloid in various states of liver disease (19)).
Urinary excretion of 166Ho-1,4,7,10-tetraazacyclododecane-1,4,7,10-tetramethylene-phosphonate in 12 subjects with multiple myeloma. (Reprinted from (18).)
Aydogan et al. (20) evaluated the uncertainty in dose estimates for an 123I-labeled brain-imaging agent (N-(3-iodopropen-2-yl)-2β-carbomethoxy-3β-(4-chlorophenyl)tropane) in 7 healthy adults (5 men and 2 women). Those investigators reported uncertainties in the fitted biokinetic coefficients and specific absorbed fractions, as obtained by first-order error propagation and Latin hypercube sampling methods. They concluded that variability in individual biokinetics and in mass could account for a doubling in the 95% confidence intervals around the point (median) dose estimates for most organs. They stated that absorbed doses that any given patient in the broad nuclear medicine population receives may be up to twice as large as the reported mean. Figure 4 shows their predicted 95% confidence interval for dose to the liver using Latin hypercube sampling modeling and taking into account all sources of uncertainty.
Ninety-five percent confidence interval predicted by Aydogan et al. (20) for dose to liver for a single agent in one patient population, using Latin hypercube sampling modeling and taking into account all sources of uncertainty.
Sparks and Aydogan (21) also evaluated the uncertainties in the extrapolation of animal data to humans, for 11 radionuclides in 33 radiopharmaceuticals, for which both extrapolated animal data and subsequent measurements in humans were available for 115 organs. Table 4 shows their observations; they found that animal data generally underpredicted the actual number of disintegrations (and thus organ self-dose) seen in humans and that the accuracy of the extrapolation was not particularly strong. No strong preference was seen for any particular extrapolation method, but what was most striking was the general lack of accuracy of the extrapolated data. Not until a factor of 10 tolerance was given were the estimates predictive in close to 90% of the cases.
Percentage of Time That Different Scaling Methods Were Successful in Predicting Human Biokinetics from Animal Data Within Specified Uncertainty Levels
CHANGES IN EFFECTIVE DOSE
The concept of effective dose was introduced by the International Commission on Radiological Protection (ICRP) in 1977 (22). To calculate effective dose, one must first convert the absorbed dose (Gy or rad) to equivalent dose (Sv or rem) by applying the appropriate radiation weighting factors (wR): Eq. 11
Eq. 11
Then, the effective dose can be calculated as the product of the individual tissue equivalent doses and the tissue-weighting factors (wT): Eq. 12
Eq. 12
In principle, the effective dose is the dose that, if uniformly received by all tissues in the body, gives the same risk of somatic and genetic effects as did the actual nonuniform dose pattern received. Although the MIRD Committee of the Society of Nuclear Medicine does not accept use of this quantity in nuclear medicine (23), the ICRP has promoted its use in nuclear medicine for diagnostic agents (24,25) and the user community has generally accepted its use. The quantity effective dose was originally derived for use in radiation protection programs. Although acknowledging the differences in age and sex distributions between the radiation worker and nuclear medicine patient population, the ICRP has endorsed use of the effective dose in nuclear medicine, noting that “Despite the wide range of organ doses in diagnostic nuclear medicine and the differences in age structure…effective dose [can be] used to provide a relative index of harm for various procedures in diagnostic radiology and nuclear medicine.” (26).
Another interesting, and perhaps unexpected, variability is introduced when effective doses are calculated using different tissue-weighting factors. The different tissue-weighting factor (wT) schemes used by the ICRP over the past 30 years for the calculation of this quantity are shown in Table 5. The recommended numeric values have changed as new information about cancer induction in various populations has been reported. Thus, given exactly the same biokinetic model and reference phantom, the effective dose calculated under 2 different sets of weighting factors will be different. Table 6 shows the differences between the dose estimates for various heart agents, using the ICRP 1979 (27) and 1991 (28) recommended weighting factors.
Tissue Weighting Factors Recommended by ICRP from 1979 to 2007
Effective Dose Values (mSv/MBq) for Various Heart Agents Based on ICRP 1979 and 1991 Weighting Factors
The risk estimates on which the tissue weighting factors are derived themselves involve large uncertainties. Figure 5 shows an excerpt from the BEIR VII report (29) on the analysis of radiation dose and effect, depicting the excess relative risk of all solid cancers from the Japanese bomb survivors. These values include all solid cancers and are averaged across both sexes and all ages; the magnitude of the uncertainties in the point estimates of risk is shown. The slope of the line is used to indicate the excess relative risk per unit dose and, eventually, the individual weighting factors for each organ system. As new information is obtained about cancer incidence and genetic risk, and as doses are recalculated, these weighting factors change and thus variability in the effective dose is introduced.
Excerpt from BEIR VII report, showing excess relative risk of all solid cancers from Japanese bomb survivors.
DOSES AT THE TISSUE OR CELL LEVEL
The discussion in this paper treats of average organ dose estimates, which are used as the basis for most routine internal dose assessments at present. Doses are also calculated, at least for research purposes, at the tissue or cellular level, and other uncertainties may be involved in these calculations. Rao et al. (30,31) showed that average organ doses are often clearly inadequate in characterizing dose–response relationships in tissues. The difference between average organ doses and tissue-level (sometimes called small-scale) doses may be substantial, in particular for low-energy, short-range electrons (32,33) and α-particles (34), for which cellular level, or “microdosimetry” (35), calculations may be needed (although average organ doses may also still be calculated (36), with the uncertainties characterized as shown in this work). Current trends point toward the idea of characterizing individual-patient 3-dimensional dose distributions within tissues using individualized image data, so that doses are characterized in small-volume elements (voxels) (37) and reported as dose distributions or dose–volume histograms. All the characterizations discussed in this section have been discussed at some length in the literature and present interesting challenges to conventional understandings of radiation dose. They also carry additional concerns regarding the uncertainty in the reported values; this issue will be left to other authors to discuss, as the practices become more widely accepted and routinely practiced.
CONCLUSION
If one could measure internal doses reliably, the uncertainties would be limited to the uncertainty in the capabilities of the measuring device at the dose level detected. Some attempts have been made in this area (38,39), but at present no reliable measurements of internal dose have become routine. Internal dose estimates based on calculational approaches depend on modeling assumptions, several of which contain significant uncertainty given the current state of the art in this area of science. The largest contributions to uncertainty are contained in the following:
The phantom-related parameters ϕ and mT—the ϕ values themselves have relatively low uncertainties, but their application to a population of individuals who vary from the median represented in the model introduces significant uncertainties, of at least tens of percentage points.
The biokinetic parameters inherent in calculation of N (or ÃS), namely fractional uptake and effective half-time in organs and the body, vary substantially across individuals. Variability by a factor of 2 or more is reasonable to assume for the kinetics of any given radiopharmaceutical. If the data are extrapolated from animal data, the dose estimates tend to underestimate the human dose estimates, and not until one uses an interval of within a factor of 10 do the animal data tend to predict the human organ dose estimates 90% of the time.
Variations in the tissue-weighting factors over time introduce an additional uncertainty of up to 20%–40% in the reported values of effective dose for diagnostic radiopharmaceuticals.
Thus, the combined uncertainties in any given radiopharmaceutical dose estimate are typically, at a minimum, a factor of 2 and may be considerably greater, in general because of normal human variability, and particularly in disease states. Similar conclusions have been reached by other authors (40,41). In therapy applications, if patient-individualized dosimetry is performed, with attention being paid to accurate data acquisition, analysis (including image quantification), processing (i.e., curve fitting), and measurement of individual organ volumes, many of the model-based uncertainties can be removed, and the total uncertainty in an individual dose estimate can be reduced to a value of perhaps ±10%–20% (8). Management of uncertainty includes collection of enough data points to characterize each phase of uptake or clearance, acquisition of enough counts for each image, and collection of data for long enough times. When data are not collected for a long enough time (e.g., until the retained activity has decreased to less than 10% of the administered activity), the available time–activity data must be extrapolated to long times after the last data point, often assuming only physical decay after this point and thereby possibly overestimating cumulated activities and radiation doses.
For diagnostic studies, reliance on standardized models for biokinetics and for body geometry will probably continue to be the normal practice, and uncertainties by factors of 2 or more in any given number are reasonable to assume. We can propagate errors in dose estimates, using what is known about population variability in body size, but knowledge of the variability of the biokinetic parameters is often more limited, and so an analytic propagation using classic methods was not attempted here. Regardless of the inherent uncertainties, calculated doses result from the careful application of the best available data and models and provide reasonable mean values for use in planning. Differences between dose estimates for any 2 radiopharmaceuticals should be appreciated and considered in the overall planning for the use of various diagnostic techniques, but small differences in dose estimates between radiopharmaceuticals should not be given too much importance when one is choosing radiopharmaceuticals for general clinical use. Diagnostic accuracy, ease of use, image quality, patient comfort, and other similar factors should predominate, with radiation dose being another important, but not defining, variable in the analysis.
Acknowledgments
This article was produced in consultation with the RAdiation Dose Assessment Resource (RADAR) Task Group of the Society of Nuclear Medicine.
Footnotes
-
COPYRIGHT © 2008 by the Society of Nuclear Medicine, Inc.
References
- Received for publication October 12, 2007.
- Accepted for publication January 22, 2008.