Abstract
Partial-volume errors (PVEs) in PET can cause incorrect estimation of radiopharmaceutical uptake in small tumors. An iterative postreconstruction method was evaluated that corrects for PVEs without a priori knowledge of tumor size or background. Methods: Volumes of interest (VOIs) were drawn on uncorrected PET images. PVE-corrected images were produced using an iterative 3-dimensional deconvolution algorithm and a local point spread function. The VOIs were projected on the corrected image to estimate the PVE-corrected mean activity concentration. These corrected mean values were compared with uncorrected maximum and mean values. Simulated data were generated as a first test of the correction algorithm. Phantom measurements were made using 18F-FDG–filled spheres in a scattering medium. Clinical validation used 154 surrogate tumors from 9 patients. The surrogate tumors were blood-pool images of the descending aorta as well as mesenteric and iliac arteries and veins. Surrogate tumors ranged in diameter from 5 to 25 mm. Analysis used 18F-FDG and 11C-CO datasets (both dynamic and static). Values representing “truth” were derived from imaging the blood pool in large structures (e.g., the left ventricle, left atrium, or sections of the aorta) where PVEs were negligible. Surrogate tumor sizes were measured from contrast CT. Results: The PVE-correction technique, when applied to the mean value in spheric phantoms, yielded recovery coefficients of 87% for an 8-mm-diameter sphere and between 100% and 103% for spheres between 13 and 29 mm. For the human studies, PVE-corrected data recovered a large fraction of the true activity concentration (86% ± 7% for an 8-mm-diameter tumor and 98% ± 8% for tumors between 10 and 24 mm). For tumors smaller than 18 mm, the PVE-corrected mean values were less biased (P < 0.05) than the uncorrected maximum or mean values. Conclusion: Iterative postreconstruction PVE correction generated more accurate uptake measurements in subcentimeter tumors for both phantoms and patients than the uncorrected values. The method eliminates the requirement for segmenting anatomic data and estimating tumor metabolic size or tumor background level. This technique applies a PVE correction to the mean voxel value within a VOI, yielding a more accurate estimate of uptake than the maximum voxel value.
PET plays an important role in the detection and staging of cancer. Whereas CT provides detailed anatomic information, PET delivers functional information to assess metabolism, metabolic size, and proliferation—critical parameters for determining the outcome of radiation therapy (1,2). Although some initial applications of PET required only the determination of the presence or absence of the radiopharmaceutical (e.g., staging), current applications require more accurate and reliable measures of relative or absolute radiopharmaceutical uptake, particularly for planning radiation treatment or for evaluating therapeutic response. Current methods for delivering external beam radiation, such as intensity-modulated radiation therapy, produce dose distributions that minimize dose to normal tissues while escalating dose to malignant regions. An integrated PET/CT system opens the door for integrating biologic volumes from PET with the anatomic volumes from CT into the process of radiation treatment planning, which traditionally has relied on anatomic information alone. The accurate localization and quantification of radiopharmaceutical uptake is expected to have an impact on conformal radiotherapy planning (3–5) and will be crucial for monitoring response to chemotherapy, especially in cases where early responses may not be detected by CT (6).
Currently, it is difficult to use PET for accurate quantitative measurements of radiopharmaceutical uptake in small tumor foci or lymph nodes because of the limited spatial resolution of PET. PET can produce inaccurate measurement of radiopharmaceutical uptake when the tumor diameter is less than twice the spatial resolution of the scanner, typically 5- to 8-mm full width at half maximum (FWHM). These errors cause incomplete recovery of counts from the tumor, by simultaneously blurring background activity into the tumor while blurring tumor activity into the background. The magnitude of this effect, known as the “partial-volume error” (PVE), depends on the size and radionuclide distribution of the tumor and adjacent background regions. Although the PVE is more apparent when measuring activity in small tumors, large tumors with necrotic centers can also be affected because the metabolically active rim is often thin compared with the size of the tumor. PVE correction will also be important if 18F-FDG PET is used as a quantitative tool for gauging response to therapy (7,8), as tumors may change in size with therapy. Finally, PVEs will be important when defining biologic tumor volumes in radiation treatment planning with PET/CT.
In an attempt to minimize PVEs, the maximum standardized uptake value (SUVmax) within a region of interest is often preferred over the volumetric mean SUV. Both are semiquantitative measures of radiopharmaceutical uptake but PVEs can cause more pronounced underestimations of mean values than of the maximum value. However, the choice of SUVmax can be problematic because it is sensitive to noise (9) and will be biased by definition. In addition, SUVmax indicates uptake only in a single pixel or a small group of pixels. The tumor, however, may have very heterogeneous uptake, and its heterogeneity may change with time or therapy. A further advantage of the SUVmean is that there is faster convergence of mean values compared with maximum values with iterative reconstruction (10). Thus, a measurement over the entire volume of interest (VOI) with correction for PVEs would be ideal.
Previous techniques for correcting PVEs can be classified into 2 categories. The first category uses a higher-resolution anatomic image from CT or MRI to define the tumor boundaries. In this case, correction for PVEs involves using the anatomic information in the image reconstruction (11) or as a model to simulate spill-in and spill-out of radioactivity to and from the VOI (12,13). One disadvantage of these methods is that they require very accurate registration of the PET and the CT or MR images at the region of interest. Inaccurate segmentation or misregistration can contribute to errors in the PVE correction. When such techniques are applied to PET/MRI of the brain they work reasonably well (14,15). However, for whole-body oncologic applications, where one wants to localize and detect tumor sites, there are pitfalls to this methodology: (a) PET metabolic and anatomic boundaries do not necessarily coincide (e.g., as in the case of necrotic tumors); (b) for patients undergoing radiotherapy, tissue scarring can make it difficult to reliably differentiate scar tissue from viable tumor using anatomic imaging alone (6); and (c) CT images do not always achieve good contrast between normal and tumor tissue, increasing the difficulty of accurately delineating the tumor for PVE correction. The second category of correction techniques also uses anatomic information, either from an additional modality (CT or MRI) or from the PET data itself. In this method, one corrects for PVEs from knowledge of how PVEs affect radionuclide quantification in tumors of various sizes and background levels. A common correction technique uses a calibrated table of correction factors (16) based on phantom measurements to adjust the SUVs. However, it is not easy to estimate the true metabolic size from the apparent size of the PET image and frequently one must assume that the tumor shape is the same as the phantom shapes studied. In addition, one needs to know the background level in the vicinity of the tumor to account for spillover from background to tumor, which can be problematic if the tumor is located close to organs with high uptake. Other authors have developed optimization models using the point spread function (PSF) to recover tumor activities (17) and size (18). These methods are often applicable only to tumors with homogeneous uptake or a particular tumor shape.
In this study, we present a fast iterative technique to correct for PVEs. The method permits the mean uptake value—rather than a maximum uptake value—to be used, potentially enabling more accurate measurement of radionuclide uptake in small tumors. The technique does not require a priori knowledge of tumor size, shape, or background level. The method is validated with computer simulations, phantoms, and patient data.
MATERIALS AND METHODS
Theory
Deconvolution is an image restoration process used to recover spatial resolution, restore edges, and improve contrast. In general, deconvolution of noisy images is an ill-posed problem because no exact solution exists. In nuclear medicine, deconvolution has been used in SPECT for improving contrast (19), performing scatter correction, and improving quantification (20). As an image restoration tool, deconvolution can lead to a significant increase in image noise level (21), especially in emission tomographic images, which already are inherently noisy. However, deconvolution techniques can be applied to PET images to estimate the level of spillover within a VOI arising from PVEs. We propose and test an iterative deconvolution technique based on Van Cittert's method (22), which can be applied to the reconstructed image. A schematic of the algorithm is shown in Figure 1 to illustrate the process of estimating the spillover within the VOI.
Schematic of iterative partial-volume-correction algorithm based on Van Cittert's algorithm (22). VOI is defined on uncorrected PET image, which is also used as initial image in iteration. Calculated spillover is used to generate the next image estimate. New PVE-corrected mean values are calculated from VOI placed on spillover-corrected image.
We denote the reconstructed PET image as Y, which can be expressed mathematically by the following equation: Eq. 1where X represents an ideal image without PVEs, A is a normalized PSF, and ⊗ is the 3-dimensional convolution operator. In general, there is no exact solution for X because of statistical noise but approximate solutions exist. Van Cittert's iterative procedure to estimate X is given as follows:
Eq. 1where X represents an ideal image without PVEs, A is a normalized PSF, and ⊗ is the 3-dimensional convolution operator. In general, there is no exact solution for X because of statistical noise but approximate solutions exist. Van Cittert's iterative procedure to estimate X is given as follows: Eq. 2where X(i) is the ith estimate of X, X(0) is estimated by Y, and α is a parameter of order 1 that affects the convergence rate. The only constraint on X(i) is that each voxel value must be positive. After X(i) is computed, the radioactivity concentration in small tumors can be estimated by drawing a VOI over the uncorrected image Y and projecting it onto the corrected image X(i) to estimate the PVE-corrected mean uptake. The nth estimate of the PVE-corrected mean uptake in the VOI is computed by averaging the uptake over the VOI. After rearranging terms in Equation 2, this average can be expressed as:
Eq. 2where X(i) is the ith estimate of X, X(0) is estimated by Y, and α is a parameter of order 1 that affects the convergence rate. The only constraint on X(i) is that each voxel value must be positive. After X(i) is computed, the radioactivity concentration in small tumors can be estimated by drawing a VOI over the uncorrected image Y and projecting it onto the corrected image X(i) to estimate the PVE-corrected mean uptake. The nth estimate of the PVE-corrected mean uptake in the VOI is computed by averaging the uptake over the VOI. After rearranging terms in Equation 2, this average can be expressed as: Eq. 3where N is the number of voxels in the VOI. Written in this way, the nth estimate of the PVE-corrected mean is expressed in terms of the mean value in the uncorrected image (Y) and a sum of correction terms. The value of α in Equation 3 typically ranges from 1 to 2 and can be dynamically set to a higher value to accelerate convergence (23). Although this algorithm works well for mean values within a VOI, the additional noise introduced can make the use of maximum values problematic. For images reconstructed iteratively, the PSF can be approximated by a 3- dimensional gaussian function. The PSF is dependent on the image location within the field of view but can be assumed to be locally invariant within the VOI. Other parameters affecting the PSF include the choice of image reconstruction algorithm and smoothing parameters. Because convolution can be performed very efficiently in Fourier space, this iterative technique is easy to implement, allowing extraction of PVE-corrected estimates of uptake knowing only the size of the local PSF.
Eq. 3where N is the number of voxels in the VOI. Written in this way, the nth estimate of the PVE-corrected mean is expressed in terms of the mean value in the uncorrected image (Y) and a sum of correction terms. The value of α in Equation 3 typically ranges from 1 to 2 and can be dynamically set to a higher value to accelerate convergence (23). Although this algorithm works well for mean values within a VOI, the additional noise introduced can make the use of maximum values problematic. For images reconstructed iteratively, the PSF can be approximated by a 3- dimensional gaussian function. The PSF is dependent on the image location within the field of view but can be assumed to be locally invariant within the VOI. Other parameters affecting the PSF include the choice of image reconstruction algorithm and smoothing parameters. Because convolution can be performed very efficiently in Fourier space, this iterative technique is easy to implement, allowing extraction of PVE-corrected estimates of uptake knowing only the size of the local PSF.
VOI Definition
Clearly, the choice and size of the VOI affects the estimate of a mean uptake value. A clinically useful method of drawing the VOI must ensure reproducibility and be applicable over a range of tumor sizes. The VOI must be large enough to reduce statistical noise and yet small enough to account for spatial heterogeneity of tumor uptake. For quantitative assessment of PVE-correction effects, a 3-dimensional VOI region-growing method was applied to the images before PV correction. The VOI encompassed all contiguous voxels having values above a fixed fraction of the maximum voxel value. Large thresholds produce small VOI sizes, which may not be suitable for tumors of <10 mm in diameter, whereas small thresholds can produce excessively large VOIs, which may extend beyond the metabolic boundaries. As will be described, empiric measurements using phantom data indicated that a threshold of 80% of the maximum value was optimum over a range of tumor sizes. This VOI then was used to extract the mean and maximum voxel values from the uncorrected dataset and the mean value from the corrected dataset. Extracted numbers were converted to recovery coefficients, defined as the ratio of measured activity concentration to the actual activity concentration.
Simulation Study
To study the convergence rate of the PVE-correction algorithm and its potential sensitivity to knowledge of the PSF, a mathematic phantom was used. This mathematic phantom was composed of spheres of various diameters (4–24 mm; voxel size = 2.0 × 2.0 × 2.0 mm3), each assigned identical uniform activity concentration. For the test of convergence rates, a noise-free phantom with no background was blurred in 3 dimensions by a gaussian PSF with a FWHM of 6.5 mm (spatial resolution of the GE Healthcare scanner used for validation with patient data). A corrected image was generated using this same PSF and applying Equation 3.
The spatial resolution of the scanner is dependent on the position within the imaging plane, and the PSF must be matched to the local resolution. This match may not always be perfect. To test the effect and tolerance of an incorrect PSF on the recovery algorithm, the FWHM values used for PVE correction of the mathematic phantoms were varied over a range of values from 5.0 to 8.0 mm.
Phantom Study
The PVE-correction algorithm also was tested with experimental data, using spheric phantoms placed inside an 18-cm-diameter water-filled cylindric phantom. Spheres having diameters of 5.0, 8.0, 13.0, 16.0, and 29.0 mm were filled with 18F-FDG at a concentration of 3.0 × 104 Bq/mL and were imaged for 3 min on a Siemens Biograph 16 (Hi-Rez) PET/CT scanner in 3-dimensional mode. A second set of data was acquired in list mode and replayed into 5 sets of 1-min and 5 sets of 3-min acquisitions. PET raw data were Fourier rebinned into 2-dimensional datasets and reconstructed iteratively using an ordered-subset expectation maximization algorithm (2D-OSEM, 4 iterations, 8 subsets, 4-mm postreconstruction gaussian filtering and CT-based attenuation correction). The transverse voxel size was 2.0 × 2.0 mm2 with a slice thickness of 2.0 mm. The radioactivity concentration from the maximum voxel value as well as the mean value from VOIs derived with region growing were both compared with PVE-corrected mean values. The PSF used for PVE correction was adjusted according to the location of the hot sphere within the field of view. The robustness of the algorithm against the noise level was tested by comparing results from the 1-min acquisitions with those from the 3-min acquisitions. Finally, the algorithm was evaluated with the presence of background activity (one fifth of sphere activity concentration).
Patient Study
The PET and CT data from 9 patients previously studied under the National Institutes of Health institutional review board–approved protocols for evaluation of renal and prostate metastases were analyzed retrospectively. Institutional review board approval to use these data was also obtained from the University of California, San Francisco. The PET images were acquired with an Advance scanner (GE Healthcare) in 2D mode, whereas CT images were acquired with a Lightspeed scanner (typically 5-mm-thick slices). Reconstructed dynamic 18F-FDG images were summed from time points of 15 to 105 s. Static 11C-CO images were acquired for 10 min beginning at least 10 min after administration (by breathing) of 370–740 MBq of 11C-CO. All images were attenuation corrected and reconstructed iteratively using OSEM (4 iterations, 28 subsets, 5-mm gaussian postreconstruction filtering with transverse voxel size of 2.0 mm and slice thickness of 4.25 mm). The 18F-FDG or 11C-CO data from the 9 patients along with separately acquired contrast CT data were analyzed using the PVE-correction technique. PVE correction was applied using a gaussian PSF with a FWHM of 6.5 mm, which matched the reconstructed resolution near the center of the PET field of view.
Because true activity concentrations of tumors could not be determined from patient data, we defined surrogate tumors using actual anatomic structures having in-plane sizes similar to those of real tumors but whose true activity concentration could be ascertained. The surrogate tumors were chosen to be 2 sequential tomographic slices of arteries or veins, with a range of diameters. We used 2 methods to determine the true activity in the surrogate tumors. The first method used 11C-CO blood-pool images for which the true concentration could be determined from venous blood samples or by imaging the cardiac left ventricular (LV) and left atrial (LA) chamber. In the latter case, a manually drawn VOI was defined within the LV and LA chamber or at sections of the aorta where its diameter was >20 mm. In both cases, PVEs would be negligible, as will be described. In the 11C-CO images, the true concentrations in the venous or arterial structures were identical regardless of their size because 11C-CO is a nearly perfect blood-pool label. Thus, any variations in apparent uptake could be attributed to statistical noise and PVEs. The vessels analyzed included the descending aorta (diameter, 12–25 mm), the superior mesenteric, inferior mesenteric, and iliac arteries, and mesenteric veins, which provided surrogate tumors from 5 to 13 mm. The second method summed the data from the very early, arterial phase of a dynamic 18F-FDG acquisition. At early time points, the 18F-FDG was still contained within the arterial vessels, permitting slices of the descending aorta and other small arterial (but not venous) vessels to be used as surrogate tumors, while producing realistic background levels similar to those in clinical images. For this second method, the small surrogate tumor was required to be located at the same bed position as a larger structure (e.g., aorta or LV/LA cavity), where the true arterial concentration in the early summed image could be determined. In all cases, the actual internal diameters of the vessels were determined from contrast CT. One hundred thirty-seven surrogate tumors were analyzed using 11C-CO data and 17 were analyzed using 18F-FDG data.
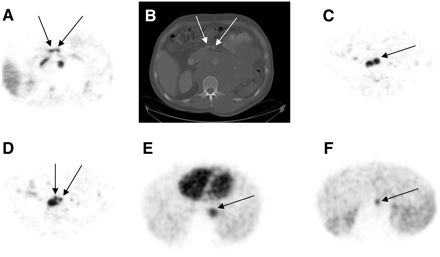
Representative surrogate tumors on PET and CT slices are shown in Figure 2. Figures 2A and 2B are examples of a 7-mm-diameter tumor defined by the superior mesenteric vein and artery from a 11C-CO study. At the abdominal level (Fig. 2C), the aorta (18-mm diameter) bifurcates into the common iliac arteries (Fig. 2D) with a diameter of about 12.5 mm. Sample surrogate tumors defined by the aorta from summed dynamic 18F-FDG PET are shown in Figures 2E and 2F.
Examples of surrogate tumors (marked with arrows) used for PVE-correction validation. (A) Superior mesenteric vein and artery (11C-CO PET). (B) Corresponding contrast CT image (used for determination of tumor diameters) at same slice location as A. (C and D) Abdominal aorta (C) and common iliac arteries (D) (11C-CO PET) after aortic bifurcation. (E and F) Descending aorta (18F-FDG PET).
Statistical Tests
All statistical comparisons were performed using 2-tailed, unpaired Student t tests with unequal variances.
RESULTS
Covergence
Although it may take several hundred iterations (23) to achieve pixel-by-pixel convergence of the deconvolved image, the mean spillover term in Equation 3 converges much more rapidly, typically in <10 iterations. This is because convergence of individual voxels within the VOI is not required to estimate the average spillover into, or out of, the VOI. Figure 3A compares the convergence rate of Equation 3 using an 80% threshold VOI for simulated 10- and 14-mm uniform hot spheric phantoms (no background) blurred by a 6.5-mm FWHM gaussian. With the convergence parameter α set to 1, it is clear that the percentage change of the spillover term between successive iterations in the 10-mm tumor converges more slowly than that for the 14-mm tumor. To improve the convergence rate, we set α to decrease from 2 to 1 in successive iterations. Preliminary benchmark results indicated that after 4 iterations, the PVE-corrected mean values were within 95% and 97% of the converged values for the 10- and 14-mm-diameter tumors, respectively. Thus, we felt that n = 4 iterations would be sufficient for our purposes, and this number of iterations was used for all validation studies.
Computer simulation. (A) Comparison of convergence rates, defined by percentage change of spillover term (second term on right-hand side of Eq. 3) between successive iterations vs. iteration number, for tumor sizes of 10 and 14 mm and α of 1 and 2. (B) Effect of PSF on recovery coefficients. Solid line, exact PSF (FWHM = 6.5 mm) used for recovery. Dashed lines, undervalued PSF (FHWM = 6.0, 5.5, and 5.0 mm) used for recovery; dashed–dotted lines, overvalued PSF (FWHM = 7.0, 7.5, and 8.0 mm) used for recovery.
PVE Correction on Mathematic Phantom
In many clinical situations, the PSF may not be known accurately and may vary slightly from one part of the field of view to another. Mathematic phantoms permitted evaluation of the correction algorithm under noise-free conditions to isolate the effect of the size of PSF on PVE correction. Figure 3B illustrates what happens when the PSF used for image recovery differs from the true PSF (i.e., a mismatch between the blurring PSF and the recovery PSF). An increase of 1 mm in the recovery PSF produced a 5%–10% increase of activity for spheres between 8 and 15 mm in diameter. The opposite trend is seen when an undervalued recovery PSF is used. On the basis of these results, we conclude that the PSF used for recovery should be within 1 mm of the true value. A slightly larger PSF could be used for better recovery of uptake in subcentimeter tumors.
PVE Correction on Physical Phantoms
The system PSF was measured using line sources located close to the center of the PET field of view of the Siemens Biograph 16 (Hi-Rez) PET/CT scanner. The FHWM value was measured to be about 4.5 mm on axis and about 5.2 mm at 5 cm off axis for both the transaxial and axial planes, which were comparable to National Electrical Manufacturers Association measurements (24) as well as to values supplied by the manufacturer. The distance of the spheres from the scanner central axis ranged from 3 to 7 cm. Depending on the sphere location, PVE correction was applied using either a 5.0-mm or a 5.5-mm FWHM gaussian. As shown in Figure 3B, and as mentioned earlier, the technique can tolerate up to 1-mm mismatch in the PSF. The value used here was either 5.0 or 5.5 mm, whichever was closest to the resolution at the sphere position. The PVE-correction algorithm was tested for 2 image noise levels (obtained from 2 different acquisition times) with no background. Replicate measurements at each noise level permitted computation of the average and SD of the recovery coefficients. The 3-min dataset (Fig. 4A, solid lines) was compared with the 1-min dataset reconstructed with the same parameters (Fig. 4A, dashed lines). As shown in Figure 4A, the uncorrected and PVE-corrected mean values from the 3-min dataset yielded recovery coefficients of 40% and 87% (P < 0.001), respectively, for an 8-mm-diameter sphere. The 13- to 29-mm-diameter spheres had uncorrected recovery ranging from 75% to 96%, whereas PVE-corrected values ranged from 100% to 103%. The corresponding maximum values were 44% at 8 mm and between 84% and 108% for the 13- to 29-mm spheres. The PVE correction produces higher and more accurate values than uncorrected maximum values for all phantoms (P < 0.01 for all spheres <16 mm diameter). For the 29-mm sphere, the maximum value overestimates the true activity concentration. The results of the higher noise (1 min) dataset were similar to those of the 3-min dataset except for a slightly lower PVE-corrected recovery coefficient at 8 mm of 71% versus 87% (P = 0.09, not significant). As expected, the higher noise level increased the size of the error bars compared with the lower noise (3 min). Finally, the SDs shown in Figure 4A are larger for the PVE-corrected data than for the uncorrected data, as expected. However, the improvement in accuracy from PV correction is far greater than the increased variability, as determined from the statistical tests and as can be confirmed visually from Figure 4A.
Phantom measurement of hot sphere recovery coefficients. (A) Influence of noise level on recovery coefficients. Solid lines, 3-min acquisition dataset; dashed lines, 1-min acquisition dataset. Error bars are 1 SD, based on 5 repeated measurements. (B) Effect of background level on recovery. Solid lines, no background activity; dashed lines, 5:1 tumor-to-background level. Error bars are 1 SD, based on 3 repeated measurements. (C) Effect of VOI threshold levels on PVE-corrected recovery coefficients.
The degree to which the background level affected the PVE correction was evaluated using 2 background levels. The result from the static phantom measurements with no background was compared with the case when the background level was one fifth the tumor activity concentration. The results are plotted in Figure 4B. For diameters of >8 mm, the effect of background on PVE recovery values was minimal. There was, however, a drop in PVE-corrected recovery coefficient for the 8-mm sphere from 85% to 65% for the 5:1 background level measurements when compared with no background (or high tumor) activity concentration. This can be attributed to the nonnegativity constraint as well as the slower convergence rates of both the OSEM reconstruction and the deconvolution of the smaller object with background activity. Despite this, the PVE-corrected mean value at 8 mm was considerably closer to unity than the non-PVE–corrected maximum value (65% vs. 42% respectively, P < 0.05).
A systematic measurement of the effect of VOI size on PVE correction was made using phantom data with no background. The results of the recovery coefficients for VOI thresholds ranging from 50% to 90% of the maximum values are plotted in Figure 4C. The 90% threshold produces small VOIs relative to the tumor size and is prone to statistical fluctuations. Because the VOIs are correlated with the maximum voxel value, the PVE-corrected mean values have a positive bias of up to 10% for diameters of >13 mm. As the threshold is reduced, the VOI starts to encompass regions beyond the tumor boundary and lead to underrecovery of tumor activity. The 80% threshold is found to be the optimum setting for images with noise levels typical of patient data and has been used for all of our PVE-correction analyses. In addition, a fixed-size VOI might also be used, although this has not been studied in this work.
PVE Correction on Patient Studies
One hundred fifty-four surrogate tumors were identified on various PET slices from the patient studies, and VOIs were defined by region growing using 80% of the maximum pixel threshold. Strictly speaking, the vessels were approximately cylindric rather than spheric, which reduced the PVE to 2 dimensions. However, most of the vessels did not lie exactly parallel to the scanner axis and did exhibit PVEs, to some degree, in the axial direction. We verified using computer simulations that the recovery coefficients of PVE-corrected mean values of a spheric phantom were 87% of the value for cylindric phantoms for diameters of 0.8 cm and almost identical for larger diameters.
The recovery coefficients derived from the surrogate tumors are plotted as a function of tumor size in Figure 5A. The PVE-corrected mean values are shown with the uncorrected mean and maximum values. The individual data points then are grouped into 2-mm bins in Figure 5B for statistical analysis. The PVE-corrected mean recovery coefficient and its SD are 86% ± 7% for an 8-mm-diameter tumor and 98% ± 8% for tumors from 10 to 24 mm. For all tumor sizes of <18 mm, the PVE-corrected mean values are significantly closer to unity (at the P < 0.05 level) than the uncorrected maximum or mean values. Even at 14 mm, the uncorrected mean value shows a negative bias of >25%. The uncorrected maximum values provide very good estimates at >16 mm but underestimate the activity by 33% at 8 mm. The PVE-corrected mean values are almost identical to the maximum values above 16 mm and recover the true activity for diameters down to 8 mm with only a 14% negative bias. Below 8 mm, the recovery coefficient curve falls off steeply, and accurate measurements of true uptake are not possible with this method. As can be seen in Figure 5B, the PVE correction does not introduce any marked increase in the SDs of the mean.
Patient data: surrogate tumor uptake recovery coefficients vs. diameter. (A) Plot of recovery coefficients before and after PVE correction with VOI defined by region growing. (B) Binned recovery coefficients and SD comparing PVE-corrected vs. uncorrected uptake as function of diameter. Points are slightly offset horizontally for clarity.
We applied the iterative deconvolution algorithm to a typical patient scan to illustrate the change in image quality achievable with 4 iterations. The original images are shown in Figures 6A and 6C, whereas the corresponding deconvolved images (displayed with the same window levels) are in 6B and 6D. As expected, deconvolution increases the visual image contrast and the intensity of small regions of focal uptake arising from PVE, at the expense of increased noise. Note that for the tumors with necrotic centers (Figs. 6C and 6D, arrows), the ratio of an ROI drawn in the bright “rind” to the necrotic center was 1.7 for the uncorrected data and 5.3 for the PVE-corrected data, using identical VOIs. Which answer is closer to truth, however, is not known. Because of increased noise in the deconvolved images, these images have not been used for identifying regions of increased uptake.
Sample patient images before (A and C) and after (B and D) image deconvolution. Note that small tumors appear darker after deconvolution and contrast is enhanced when displayed at same window level. Amplification of noise is apparent in B and D and should be used with caution.
DISCUSSION
The deconvolution methodology described to correct for PVEs can be applied retrospectively, even with data acquired on a dedicated PET scanner. No assumptions regarding tumor size, homogeneity, or background are necessary. A careful measurement and tabulation of the position- dependent PSF for specific reconstruction parameters is required, although, as shown in Figure 3B, the PSF used for PVE correction need only be within 1 mm of the true value. For the PET/CT scanner used in the phantom studies (Biograph; Siemens Medical Solutions USA, Inc.), the spatial resolution increases by about 1 mm at 10 cm (24) from the scanner isocenter. In our validation, the surrogate tumors and phantoms were typically located within 10 cm from the center of the field of view and, thus, permitted us to use a PSF corresponding to the resolution near the axis. Thus, correction of a whole-body image can be performed by subdividing it into several regions where the PSF can be assumed to be locally invariant in each subsection. For spheric phantom tumors of <16 mm in diameter, the PVE-corrected mean values were shown to give significantly more accurate tumor uptake values than uncorrected mean or maximum values, despite the increased noise resulting from the PVE correction. This finding in the phantom studies was echoed in the clinical patient studies using surrogate tumors. The PVE-correction technique gave similar results for both the low noise (3-min acquisition) and the higher noise (1-min acquisition) phantom studies. The error bars in the patient data (Fig. 5) give a good indication of the variability and reproducibility as a function of tumor size, in actual clinical images. In real patients, motion (e.g., from breathing) can lead to additional blurring, which is not considered in the PVE correction performed here. Thus, it is not surprising that recovery coefficients were slightly worse for small tumors in real patients compared with phantom measurements. This would presumably be true regardless of the PVE-correction technique applied. The ability to use a partial-volume-corrected mean value, rather than the usual maximum value, avoids the known problems associated with a maximum value—primarily its dependence on statistical noise, and, hence, its dependence on magnitude of uptake, reconstruction parameters, and so forth.
Apart from facilitating improved quantitative estimates of uptake in small tumors in oncology, this method could presumably be used to derive accurate image-based input functions for cardiac studies (25,26) or for kinetic modeling to extract glucose use rates (27,28) using any visible section of the aorta, even if the LV is not in the field of view. One might also use deconvolution as a tool for delineating tumor boundaries in conformal radiotherapy. To our knowledge, none of these potential applications has yet been tested.
One might be tempted to treat a deconvolved image as an improved image with reduced PVEs (29), but a potential pitfall is the increased likelihood of false-positive findings arising from noise amplification (Fig. 6). In this article, we have not addressed this issue and, instead, have focused on the use of deconvolution to obtain better quantitative estimates of uptake in tumors whose sizes are as small as the spatial resolution of the scanner. Until further studies are available, it is proposed that visual clinical decisions be made on the original, uncorrected images, but uptake measurements (e.g., SUV) be made using data from the PVE-corrected images. Without any correction, PVEs can underestimate uptake by >50% for tumors of <1 cm.
A major assumption made in our PVE-correction method is that the spatial resolution of the reconstructed PET image does not change with the activity level or distribution. This seems to be a reasonable assumption with proper randoms correction and with the current advanced-generation iterative reconstruction techniques incorporating scatter correction. We also have assumed that a sufficient number of iterations have been used to reconstruct the image such that the spatial resolution within the image does not significantly depend on the size of the object (30). In principle, the deconvolution step could be built into the iterative reconstruction, but this would be of general clinical use only after manufacturers had incorporated these algorithms in their software. The postreconstruction method described here would be of immediate use for all current-generation PET scanners.
Other variations of iterative techniques (23) could presumably also be used in the PVE-correction algorithm. The method used here requires <10 iterations to achieve convergence (Fig. 3A), despite the fact that the corrected image may not have converged on a pixel-by-pixel level. Good recovery values were achieved even for 4 iterations, as shown herein. Instead of using a fixed number of iterations, one could also use the rate of change of the mean value between iterations as a stopping parameter for the iterative process. A higher number of iterations would be used for smaller tumors, where the convergence rate is slower.
CONCLUSION
An iterative technique has been developed to correct for PVEs in PET images. The method has been tested with digital phantoms, physical phantoms, and real patient data. Unlike other PVE-correction techniques, no assumptions regarding tumor size, homogeneity, boundary, or background level are required. No ancillary morphologic image or image segmentation is required, making the method simple to implement. The method produces mean tumor uptake values that are significantly more accurate than either uncorrected mean or maximum values. Because the technique is applied after image reconstruction, it can be used in existing clinical PET scanners to improve quantitative accuracy of tracer uptake in subcentimeter tumors.
Acknowledgments
This work was supported in part by grants from Siemens Oncology Care Systems and the University of California Industry–University Cooperative Research Program (grant dig-itl04-10174).
Footnotes
-
COPYRIGHT © 2007 by the Society of Nuclear Medicine, Inc.
References
- Received for publication August 14, 2006.
- Accepted for publication February 7, 2007.