Abstract
The purpose of this study was to evaluate the therapeutic efficacy and limitations of α-particle-emitting radiolabeled compounds by means of 2-dimensional histological images and distribution of activity on a microscopic level. Methods: A microdosimetric approach based on histological images is used to analyze the therapeutic effectiveness of α-particle-emitting 211At and 213Bi conjugated to 201B monoclonal antibody (mAb), which is reactive with murine lung blood vessels for the treatment of EMT-6 lung tumor colonies in nude mice. Autoradiography images were used to define the tissue morphology and activity distribution within lung tissues. Two animal groups were studied: Group A consisted of animals bearing small tumors (<130 μm) and group B consisted of larger tumors (<600 μm). Probability density functions (pdf) described the variability in average absorbed dose and survival probability among normal and tumor target cells and, in turn, were used to assess the survival fraction of tumor and normal tissue. Results: The average absorbed dose to tumor cells per unit cumulated activity concentration for animals in group A was 1.10 × 10−3 and 1.37 × 10−3 Gy g MBq−1 s−1 for 211At and 213Bi, respectively, and for animals in group B was 3.8 × 10−4 and 5.6 × 10−4 Gy g MBq−1 s−1 for 211At and 213Bi, respectively. The fraction of tumor cells that received a zero absorbed dose for animals in group A was 0.04% for 213Bi and 0.2% for 211At and for animals in group B was 25% for 213Bi and 31% for 211At. Both 213Bi- and 211At-labeled 201B mAb were effective therapies for animals with small tumors, where predicted therapeutic effectiveness was consistent with experimental findings; however, they were ineffective for animals with larger tumors. Conclusion: Microdosimetric methods based on knowledge of tissue morphology and activity distribution on a small-scale level can be a useful tool for evaluating a priori the therapeutic efficacy and limitations of targeted α-particle endoradiotherapeutic strategies.
Various strategies using α-particle-emitting radionuclides are being investigated for the targeted endoradiotherapy of a diversity of malignancies. Many of these efforts involve the use of 7.2-h and 46-min half-life radionuclide 211At- and 213Bi-labeled monoclonal antibodies (mAbs) reactive with tumor- or vascular-associated antigens. These studies range from evaluation in animal models of human disease to clinical trials in patients with leukemia and glioma (1–8). However, current conventional dosimetric approaches are limited in interpreting their radioimmunotherapeutic efficacy and, therefore, methods for dosimetry analysis at the small-scale level must be developed to understand their effectiveness and limitations. Because of the short range in tissue of α-particles (<100 μm) and the highly heterogeneous cumulated activity distribution that can be encountered with targeted radiotherapeutics, the absorbed dose and corresponding survival probability for individual target cells can vary considerably from those encountered at a uniform activity distribution, which is assumed in conventional dosimetry when there is a lack of information at the small-scale level. Furthermore, this may be particularly problematic in antivascular strategies where the radiotherapeutic is targeted to tumor blood vessels and, thus, heterogeneously deposited within the tumor mass.
The use of cellular conversion factors or S values for α-particles can be a misleading oversimplification of the activity heterogeneity, both in distribution and in intensity, that would be encountered in vivo (9–13). The widely used assumption of source uniformity among different source-target combinations is not applicable at the microscopic level required for analyzing α-particle effectiveness. Furthermore, the use of these arithmetic methods can lead to a considerable overestimate in tumor absorbed dose at the cellular level (14). Also, they do not provide an estimate of the cell survival probability to individual target cells, in microdosimetric terms, and overall survival fraction. A more realistic, albeit tedious, approach requires the precise determination of the spatial location of the tumor and normal target cells and of the activity distribution in tissue. This can be accomplished by obtaining autoradiographic images, which can provide more realistic information for assessing the microdosimetry and survival fraction of tumor cells in a particular tissue sample (15–17). However, it is important to consider that there are certain limitations and uncertainties associated with the handling and use of histological and autoradiography images for dosimetric purposes, which have been described and reviewed in detail by Humm et al. (18).
The microdosimetry of α-particles can be carried out deterministically based on convolution methods using functional forms as long as there is 1 medium with a uniform density (19). However, with lung and bone tissues deterministic approaches are difficult to apply because >1 media are involved. In these circumstances, a Monte Carlo approach is suitable because changes in media can be incorporated easily (20). Once the microdosimetry for each individual target cell is estimated, it is then possible to perform a statistical analysis where microdosimetric results can be presented in the form of probability density functions pdf, similar in concept to the dose-volume histogram used in external beam radiotherapy, to describe the variability in absorbed dose and survival probability among all tumor target cells. In this manner, it is possible to estimate the overall survival fraction as a function of cumulated activity concentration. To express this variability in practical terms, we introduce the concept of over-dose fraction, under-dose fraction, and zero-dose fraction. These terms provide a convenient means of comparison with results that would be obtained under the assumption of a uniform dose distribution, hopefully yielding an understanding of the overall effectiveness and limitations of a particular therapy strategy.
In this article, we describe a set of microdosimetric methods for evaluating the response to targeted α-particle endoradiotherapy based on histological images. We have applied these methods to assess and compare the absorbed dose and survival probability of EMT-6 mammary carcinoma lung tumor colonies after treatment of mice with 211At- and 213Bi-labeled 201B, a mAb that reacts with an antigen present in lung vascular endothelial cells.
MATERIALS AND METHODS
Animals, Tumor Cell Line, and mAb
BALB/c female mice (8 wk old) were inoculated intravenously with 2 × 104 EMT-6 mammary tumor cells in 200 μL phosphate-buffered saline to generate an average of 100 lung colonies per mouse growing perivascularly (7). The 201B mAb is reactive with murine thrombondulin and localizes rapidly in mouse lung endothelium (7,21,22). Animals were inoculated and lung tumor colonies were allowed to grow for a period of 5 d (group A) and 8 d (group B) before intravenous therapy with 211At- or 213Bi-labeled 201B mAb. For autoradiography purposes, 1 animal from each group was injected with 0.22–0.26 MBq 125I-labeled 201B mAb and was killed 30 min after injection to assess the morphologic characteristics of tumor lung colonies and the activity distribution of radiolabeled 201B mAb at the time of therapy with either 211At- or 213Bi-labeled 201B mAb. A detailed description of the therapeutic protocols and responses observed can be found for 213Bi (7,21,22) and for 211At (23).
Lung Histological Images and Autoradiography Data
Immediately after animals A and B were killed, the lungs were reinflated with 0.6 mL neutral buffered formalin through a 22-gauge tracheal catheter to reestablish their natural morphology. The inflated lungs were then excised and submerged in buffered formalin for 24 h before processing for paraffin sectioning. For each animal, 20 serial (5- to 6-μm thick) paraffin sections were cut and every other slice was dipped in NTB-2 emulsion (Kodak, Rochester, NY) for autoradiographic evaluation. The slides were exposed for 5 d, developed, and stained with hematoxylin-eosin (6). Color images were obtained from histological samples. Tumor and normal lung cells were distinguished on the basis of their morphology. Tumor clusters were compact, showing a larger nucleus than normal lung cells with a very well-defined boundary. For the purposes of this microdosimetry study, it was assumed that the distribution of 125I activity was representative of that of 213Bi and 211At within lung tissue. The dimensions of the images were 640 × 480 pixels with a pixel size of 4.08 μm. Using image analysis software, the following were identified in every autoradiography image and saved in 16-bit binary form: (a) a source image describing the distribution and intensity of activity, (b) a target image describing the pixels that were identified as target cells (normal and tumor cells), and (c) an image identifying the regions of air, alveolar space, and tissue. These images were then used as input data for an α-particle Monte Carlo transport code to assess the energy deposition patterns and corresponding microdosimetric calculations for 211At and 213Bi. The activity distribution determined in these autoradiography images was assumed to be time independent—that is, redistribution of the radiolabeled compound was assumed to be negligible. The limitations associated with the use of histological and autoradiographic images have been described in detail elsewhere (18). Using a ×40 lens objective, area measurements of the cross-sections of the nucleus of tumor and normal lung tissue were carried out. The 3-dimensional (3D) average nuclear radius r̄n was estimated as r̄n = 1.27r̄c, where r̄c is the average nuclear cross-sectional radius obtained from histological images. A similar calculation was carried out to assess the cell radius.
α-Particle Monte Carlo Transport
Monte Carlo transport of α-particles was carried out on every histological image using a code developed in-house (20). We used this approach to α-particle microdosimetry on the basis of 2-dimensional (2D) histological images, which can be considered as the equivalence of a single 2D cross-section passing through a large number of cells randomly oriented within a 3D tissue sample, and a large number of randomly oriented planes sampled from a single cell within the 3D cell tissue having an anatomy representative of its morphologic surroundings. This is considered as a reciprocity principle, where a single 2D autoradiography image provides the activity distribution of the radiolabeled compound and the random section through the cells intersected by such plane (24).
On a 2D image, the trajectory of every α-particle was followed as it traversed each region of air or tissue where the specific energy deposition z, number of hits n, and survival probability per event T1,z0 as a function of cell sensitivity z0 were recorded for every target cell identified on the image. It was assumed that a tumor cell was located at the center of every identified target pixel, and every time an α-particle traversed the pixel calculations were made to assess the specific energy deposition to the cell nucleus with previously determined dimensions. The stopping powers used for α-particle transport purposes were those of air and tissue with densities of 1.20 × 10−3 and 1.04 g cm−3, respectively (25). The maximum range of the α-particles from 211At and 213Bi (and daughters) in tissue is 71 and 85 μm, respectively, and in air they are 6.9 and 8.1 cm, respectively. The sampling of the spatial coordinates (x, y) was based on the activity distribution using a double rejection technique where the indices i and j were determined in reverse order, and then a random sampling was carried out within the pixel to assess the initial coordinates x and y. The z-coordinate was sampled randomly between (−rcell, rcell). In this manner, it was possible to take into consideration the heterogeneity and intensity of activity within a tissue sample (26). Because 201B mAb is not known to internalize, the activity distribution was assumed to be located on the surface of cells; thus, for an event to be recorded, the trajectory length s of an α-particle must be higher than or equal to the cell diameter—that is, s ≥ 2rcell.
Microdosimetry and pdf
Let us assume a small-scale volume ν of tissue with a heterogeneous cumulated activity distribution, with mass mTissue and total cumulated activity Ã; and let q = Ã/mTissue be the average cumulated activity concentration over the entire volume ν. Thus, for any given target cell, the average specific energy per event z̄1 and survival probability per event T1,z0 can be calculated directly by means of Monte Carlo transport. Thus, z̄1 and T1,z0 are estimated as:
 and
and
 Eq. 1 respectively, where n is the total number of recorded events, zi is the specific energy deposition of event i, and z0 is the cell sensitivity of the target cell. Thus, the average specific energy z̄ and the survival probability Tz0 are then simply given as:
Eq. 1 respectively, where n is the total number of recorded events, zi is the specific energy deposition of event i, and z0 is the cell sensitivity of the target cell. Thus, the average specific energy z̄ and the survival probability Tz0 are then simply given as:
 and
and
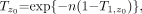 Eq. 2 where the probability that a target cell having a zero absorbed dose or zero hits is given by Tz0(z = 0) = exp [−n] (27). On the basis of the mean value theorem, the standard deviation σz̄1 for the average specific energy per event z̄1 for every identified target was estimated. When ςz̄1/z̄1 was below 1% for all identified targets with z̄1 > 0, the Monte Carlo transport was then halted. Let n̂ = n/q be the normalized average number of hits defined as the average number of hits per unit cumulated activity concentration in volume ν. Thus, the average specific energy z̄ and survival probability Tz0 can be rewritten as z̄ = qn̂z̄1 and Tz0 = exp{−qn̂(1 − T1,z0)} or as:
Eq. 2 where the probability that a target cell having a zero absorbed dose or zero hits is given by Tz0(z = 0) = exp [−n] (27). On the basis of the mean value theorem, the standard deviation σz̄1 for the average specific energy per event z̄1 for every identified target was estimated. When ςz̄1/z̄1 was below 1% for all identified targets with z̄1 > 0, the Monte Carlo transport was then halted. Let n̂ = n/q be the normalized average number of hits defined as the average number of hits per unit cumulated activity concentration in volume ν. Thus, the average specific energy z̄ and survival probability Tz0 can be rewritten as z̄ = qn̂z̄1 and Tz0 = exp{−qn̂(1 − T1,z0)} or as:
 and
and
 Eq. 3 where ẑ = n̂z̄1 is defined as the normalized absorbed dose, which is the average absorbed dose to a target cell per unit cumulated activity concentration, and T̂z0 = exp{−1·n̂(1 − T1,z0)} is defined as the normalized survival probability, which is the survival probability per unit cumulated activity concentration (i.e., q = 1). The units for ẑ are Gy g MBq−1 s−1 and for T̂z0 are unitless. Thus, it is possible to express the average absorbed dose z̄ and survival probability Tz0 to a given target cell in terms of q; for numeric convenience, q is expressed in units of MBq s g−1. Moreover, the probability for a target cell receiving zero hits is given as Tz0(z = 0) = [e−n̂]q, where T̂z=0 = e−n̂, which is defined as the normalized probability of zero-hits.
Eq. 3 where ẑ = n̂z̄1 is defined as the normalized absorbed dose, which is the average absorbed dose to a target cell per unit cumulated activity concentration, and T̂z0 = exp{−1·n̂(1 − T1,z0)} is defined as the normalized survival probability, which is the survival probability per unit cumulated activity concentration (i.e., q = 1). The units for ẑ are Gy g MBq−1 s−1 and for T̂z0 are unitless. Thus, it is possible to express the average absorbed dose z̄ and survival probability Tz0 to a given target cell in terms of q; for numeric convenience, q is expressed in units of MBq s g−1. Moreover, the probability for a target cell receiving zero hits is given as Tz0(z = 0) = [e−n̂]q, where T̂z=0 = e−n̂, which is defined as the normalized probability of zero-hits.
For every histological image, the microdosimetry results for n̂, ẑ, T̂z0 were recorded for all identified target cells, analyzed statistically, and expressed in terms of pdf. A pdf was then calculated for the normalized average absorbed dose ẑ, average specific energy per event z̄1, survival probability per event T1,z0, and normalized survival probability per unit cumulated activity concentration T̂z0. Once the survival probability Tz was estimated for all individual target cells, it was possible to assess the survival fraction SF as a function of cumulated activity concentration q for a given cell sensitivity z0 as:
 Eq. 4
Eq. 4
For the ideal case of a uniform activity distribution under charged particle equilibrium (in terms of expectation values, a volume ν is under charged particle equilibrium [CPE] conditions if each charged particle of a given energy leaving the volume ν is replaced by an identical particle of the same type and energy entering the volume ν.) conditions, the normalized absorbed dose 〈ẑ〉 is independent of cell morphology and it is simply given by the energy emitted per unit mass per unit cumulated activity concentration. For the case of 211At and 213Bi, 〈ẑ〉u is 1.086 × 10−3 and 1.334 × 10−3 Gy g MBq−1 s−1, respectively. Thus, we defined the uniform average normalized absorbed dose 〈ẑ〉u and uniform average normalized survival probability 〈T̂z)〉u as:
 Eq. 5 and
Eq. 5 and
 Eq. 6 respectively, which were later on used as thresholds for statistical analyses. Thus, in terms of expectation values 〈ẑ〉u = 〈z1〉u〈n̂〉u, and the expected D0u value for a uniform activity distribution is then given as:
Eq. 6 respectively, which were later on used as thresholds for statistical analyses. Thus, in terms of expectation values 〈ẑ〉u = 〈z1〉u〈n̂〉u, and the expected D0u value for a uniform activity distribution is then given as:
 Eq. 7 which is the required absorbed dose to reduce the survival fraction to e−1.
Eq. 7 which is the required absorbed dose to reduce the survival fraction to e−1.
Average Survival Fraction, S̅F̅
The survival fraction from a single reconstructed histological image is not representative of a tumor; consequently, it is necessary to analyze multiple histological samples and statistically combine their survival fractions to obtain a more meaningful value. The weighted survival fraction from multiple histological images is given as:
 Eq. 8 where q̄ is the mass-weighted average cumulated activity concentration among all samples, given as:
Eq. 8 where q̄ is the mass-weighted average cumulated activity concentration among all samples, given as:
 Eq. 9 and the coefficients λi, κi, and wi are:
Eq. 9 and the coefficients λi, κi, and wi are:
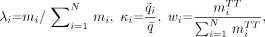 Eq. 10 where mi is the tissue mass and miTT is the tumor tissue mass for reconstructed sample i. The average survival fraction S̅F̅ for 211At and 213Bi was estimated from a total of 24 and 34 reconstructed histological images from lungs of animals A and B, respectively.
Eq. 10 where mi is the tissue mass and miTT is the tumor tissue mass for reconstructed sample i. The average survival fraction S̅F̅ for 211At and 213Bi was estimated from a total of 24 and 34 reconstructed histological images from lungs of animals A and B, respectively.
Under-Dose Fraction F<, Over-Dose Fraction F>, Zero-Dose Fraction F0, and Probability of Tumor Incidence pti
The activity distribution in tissues from intravenously administered radiotherapeutics generally is heterogeneous due to a variety of pharmacokinetic and biologic factors. These include tumor blood flow, radioligand permeability, diffusion and convection constraints, penetrability, antigen or receptor density, binding kinetics, and residence time, all leading to a heterogeneous distribution when the tissue is evaluated at the small-scale level (28). This is particularly likely when the radiolabeled compound binds to blood vessels and not to tumor cells. Consequently, many tumor regions may be left untreated; thus, the resulting pdf for ẑ and T̂z0 will differ from that for a uniform activity distribution. To reflect such regional variations in tumor dose deposition, we introduce here the concept of under-dose fraction F<, over-dose fraction F>, and zero-dose fraction F0 to provide a means of evaluating the absorbed dose and survival probability variations for target cells resultant from a given therapeutic strategy. Therefore, setting the average normalized absorbed dose for a uniform activity distribution 〈ẑ〉u as a threshold, the pdf(ẑ) can be divided into the following regions: the under-dose fraction F< is the area where ẑ < 〈ẑ〉u, the over-dose fraction F> is the area where ẑ > 〈ẑ〉u, and the zero-dose fraction F0 is given when ẑ = 0, which are given as:

 and
and
 Eq. 11 respectively, where ∂(ẑ) represents the delta function. An equivalent partition can be estimated using the average normalized survival probability for a uniform activity distribution 〈T̂z)〉u as a threshold and the pdf(T̂z0) for the normalized survival probability, where F> = ∫0〈T̂z0〉u pdf(T̂z0)dT̂, F< = ∫〈T̂z0〉u1 pdf(T̂z0)dT̂, and the zero-dose fraction corresponding to T̂ = 1 as F0 = ∫01 pdf(T̂z0)∂(T̂ − 1)dT̂. The use of probability density functions for the normalized absorbed dose pdf(ẑ) is similar in concept to a dose-volume histogram in external beam therapy. A similar statistical analysis for several histological images, as described above, can be carried out to assess the average over-dose fraction F̄>, average under-dose fraction F̄<, and average zero-dose fraction F̄0 from multiple samples.
Eq. 11 respectively, where ∂(ẑ) represents the delta function. An equivalent partition can be estimated using the average normalized survival probability for a uniform activity distribution 〈T̂z)〉u as a threshold and the pdf(T̂z0) for the normalized survival probability, where F> = ∫0〈T̂z0〉u pdf(T̂z0)dT̂, F< = ∫〈T̂z0〉u1 pdf(T̂z0)dT̂, and the zero-dose fraction corresponding to T̂ = 1 as F0 = ∫01 pdf(T̂z0)∂(T̂ − 1)dT̂. The use of probability density functions for the normalized absorbed dose pdf(ẑ) is similar in concept to a dose-volume histogram in external beam therapy. A similar statistical analysis for several histological images, as described above, can be carried out to assess the average over-dose fraction F̄>, average under-dose fraction F̄<, and average zero-dose fraction F̄0 from multiple samples.
We further define the probability of tumor incidence, pti, as:
 Eq. 12 where N(F0 > 0) is the number of histological samples analyzed with a zero-dose fraction higher than zero, F0 > 0, and Nsamples is the total number of samples. The variable pti is a measure of the potential for tumor remaining after therapy; thus, the probability that x number of animals will exhibit tumor will be given by a binomial distribution Φ(x, Nsample, μ), where μ = pti represents the probability of histological tumor observation.
Eq. 12 where N(F0 > 0) is the number of histological samples analyzed with a zero-dose fraction higher than zero, F0 > 0, and Nsamples is the total number of samples. The variable pti is a measure of the potential for tumor remaining after therapy; thus, the probability that x number of animals will exhibit tumor will be given by a binomial distribution Φ(x, Nsample, μ), where μ = pti represents the probability of histological tumor observation.
Localized Therapeutic Inequality
We have defined a potentially successful endoradiotherapy strategy as one for which the following inequality between normal and tumor tissue cells is established (19):
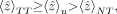 Eq. 13 which are referred here to as the localized therapeutic inequality, where TT represents tumor tissue and NT represents normal tissue. This inequality states that the average normalized absorbed dose to tumor tissue must be equal to or higher than that obtained under a uniform activity distribution under CPE conditions and that the average normalized absorbed dose to normal tissue must be lower than that under a uniform activity distribution. Accordingly, we defined the tumor tissue CPE ratio as 〈ẑ〉uTT = 〈ẑ〉TT/〈ẑ〉u and the normal tissue CPE ratio as 〈ẑ〉uNT = 〈ẑ〉NT/〈ẑ〉u, which were used as an indicator for comparison purposes of CPE conditions for a given therapy. For a given tissue volume, the inequality wTT〈ẑ〉uTT + wNT〈ẑ〉uNT ≤ 1 was also established, where wTT and wNT are the mass fraction of tumor and normal tissue, respectively. If the tissue volume under consideration was under CPE conditions, then wTT〈ẑ〉uTT + wNT〈ẑ〉uNT = 1. The inequality is independent of the type of radiation emissions (β- or α-particles) and CPE conditions. In practical terms, one would expect that a successful therapy strategy would comply with this inequality to obtain a favorable therapeutic outcome while minimizing the dose to normal tissues. Therefore, the efficacy of a strategy is established by the inequality 〈ẑ〉uTT ≥ 1 > 〈ẑ〉uNT.
Eq. 13 which are referred here to as the localized therapeutic inequality, where TT represents tumor tissue and NT represents normal tissue. This inequality states that the average normalized absorbed dose to tumor tissue must be equal to or higher than that obtained under a uniform activity distribution under CPE conditions and that the average normalized absorbed dose to normal tissue must be lower than that under a uniform activity distribution. Accordingly, we defined the tumor tissue CPE ratio as 〈ẑ〉uTT = 〈ẑ〉TT/〈ẑ〉u and the normal tissue CPE ratio as 〈ẑ〉uNT = 〈ẑ〉NT/〈ẑ〉u, which were used as an indicator for comparison purposes of CPE conditions for a given therapy. For a given tissue volume, the inequality wTT〈ẑ〉uTT + wNT〈ẑ〉uNT ≤ 1 was also established, where wTT and wNT are the mass fraction of tumor and normal tissue, respectively. If the tissue volume under consideration was under CPE conditions, then wTT〈ẑ〉uTT + wNT〈ẑ〉uNT = 1. The inequality is independent of the type of radiation emissions (β- or α-particles) and CPE conditions. In practical terms, one would expect that a successful therapy strategy would comply with this inequality to obtain a favorable therapeutic outcome while minimizing the dose to normal tissues. Therefore, the efficacy of a strategy is established by the inequality 〈ẑ〉uTT ≥ 1 > 〈ẑ〉uNT.
Pharmacokinetics of 201B mAb and Lung Residence Time
The microdosimetric analysis presented above describes the average survival fraction S̅F̅ as a function of average cumulated activity concentration in lung tissue q̄. However, there is the need to establish a relationship between the initial administered activity A and the average cumulated activity concentration q̄ of radiolabeled 201B mAb in lung tissue. We used the uptake and clearance data obtained from previous animal experiments (21) (data not shown) and established a compartmental model to assess the residence time in lung tissue for 211At-, 213Bi-labeled 201B mAb. For the purpose of these calculations, it was assumed that the lung tissue distribution of the different mAb labels was the same and any radionuclide daughters were assumed to decay at the site of the parent radionuclide (1-dimensional layer). Figure 1 presents the compartmental model and corresponding transfer coefficients. Solutions to this compartmental model were obtained using an inverse matrix method for compartmental recycling (29). The physical half-lives for 211At and 213Bi, are 7.21 and 0.76 h, respectively, which correspond to a physical residence time of 10.41 and 1.10 h, respectively. The estimated residence time (percentage) in lung tissue for 211At and 213Bi was 4.09 h (39%) and 0.36 h (33%), respectively. Consequently, the administered activity A was given as:
 Eq. 14 where q̄lung is the average cumulated activity concentration in lung tissue and the lung mass mlung was estimated to be 0.11 g. Therefore, it was possible to express the average survival fraction S̅F̅ as a function of initial administered activity A for each radiolabeled mAb.
Eq. 14 where q̄lung is the average cumulated activity concentration in lung tissue and the lung mass mlung was estimated to be 0.11 g. Therefore, it was possible to express the average survival fraction S̅F̅ as a function of initial administered activity A for each radiolabeled mAb.
RESULTS
Microdosimetry of 211At and 213Bi Assuming Uniform Activity Distribution
From measurements made directly from histological images, the estimated average cell and nuclear radius for EMT-6 cells was 4.4 and 3.9 μm, respectively, and for normal lung cells it was 3.7 and 3.2 μm, respectively. Using these cell geometries, microdosimetry calculations for 211At and 213Bi were carried out assuming a uniform activity distribution where the normalized absorbed dose 〈ẑ〉u and the normalized survival probability 〈T̂z0〉u were used as thresholds for comparison purposes to the microdosimetric calculations described below based on histological images. The probability density function for the normalized absorbed dose pdf(ẑ) and for the normalized survival probability pdf(T̂z0) for a uniform activity distribution resulted in a symmetrically truncated gaussian distribution. A summary of the microdosimetric results is provided in Figure 2. Irrespective of cell morphology, the normalized absorbed dose for a uniform activity distribution, given by 〈ẑ〉u = 〈n̂〉u〈z̄1〉u, for 211At and 213Bi was 1.086 × 10−3 and 1.334 × 10−3 Gy g MBq−1 s−1, respectively. The normalized probability for a cell receiving zero hits is given as T̂z=0 = exp [−1·〈n̂〉u], where q = 1 MBq s g−1, when q → ∞ then Tz=0 → 0. Figure 2A shows the average survival probability per event 〈T1〉u as a function of cell sensitivity for tumor and normal lung tissue for 211At and 213Bi. Figure 2B shows the average normalized survival probability 〈T̂z0〉u as a function of cell sensitivity z0. Figure 2C shows the survival fraction SF as a function of cumulated activity concentration for 211At and 213Bi for a cell sensitivity value of 0.1 Gy for tumor and normal lung tissue. Figure 2D shows D0u(z0), the required dose to reduce the SF to e−1, as a function of cell sensitivity z0 for 211At and 213Bi for tumor and normal lung tissue.
Microdosimetry of 211At and 213Bi and Survival Fraction for Tumor and Normal Tissue from Histological Images
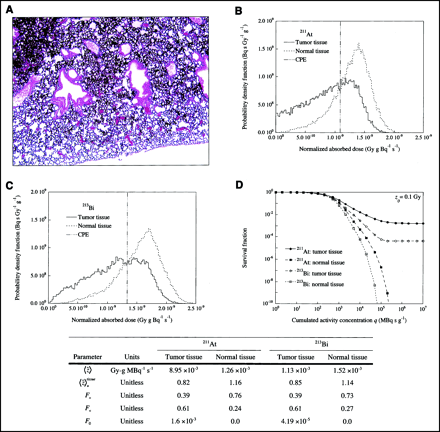
These microdosimetry calculations were based on lung histological images obtained from mice injected intravenously with EMT-6 tumor cells and killed 5 d (animal A) and 8 d (animal B) after tumor cell inoculation and 30 min after 125I-labeled 201B mAb injection. There was a total of 24 and 36 reconstructed histological images from animals A and B, respectively. As shown in Figure 3, tumors in animal A were more diffuse along the perivascular space of the lungs, whereas animal B had solid tumor nodules. Tumor sizes in both animals varied considerably within a given image and among images. The estimated average (range) tumor chord length in animal A was 42 μm (8–130 μm) and for animal B it was 130 (40–600 μm). For the case of animal B, the average chord length was greater than the maximum tissue range of either 211At or 213Bi α-particles. The average (range) fraction of the histological image that was composed of tumor was 0.17 (0.06–0.34) and 0.27 (0.13–0.49) for animals A and B, respectively. On the basis of an estimated lung mass of 0.11 g, the estimated average (range) lung tumor mass for animals A and B was 0.019 g (0.006–0.038 g) and 0.030 g (0.014–0.054 g), respectively.
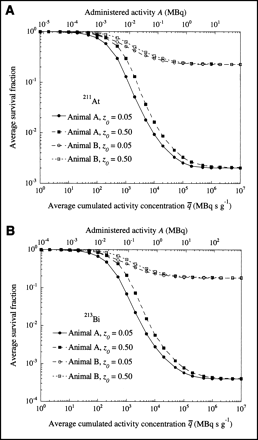
Microdosimetric analysis for 211At and 213Bi was carried out for each reconstructed histological image. The pdf for the normalized absorbed dose ẑ, the normalized survival probability T̂, and the survival fraction SF, as a function of cumulated activity concentration q, were calculated for normal and tumor tissue cells. Figures 4 and 5 summarize the results for a typical histological image obtained from animals A and B, respectively. The survival fraction SF for either normal tissue or tumor tissue for 213Bi was lower than that for 211At for a given cumulated activity concentration. This effect was reflected by the shorter range in tissue of α-particles emitted by 211At compared with 213Bi, resulting in a smaller zero-dose fraction F0 for 213Bi.
A summary of the microdosimetry analyses from all histological images for normal lung and tumor tissue is given in Table 1 for 211At and 213Bi. Because 201B mAb targets the vascular endothelium of normal lung, irradiation of normal lung tissue was anticipated. This resulted in more energy being deposited in normal lung tissue than in tumor tissue for both animals A and B and, consequently, the resulting energy partition and dose distribution between normal and tumor tissues did not comply with the localized therapeutic inequality set as a criterion for targeted radiotherapeutics.
The tumor mass-weighted average (range) zero-dose fraction F̄0 for animal A was 2 × 10−3 (0.0–0.024) and 4 × 10−4 (0.0–0.011) for 211At and 213Bi, respectively, whereas the probability of tumor incidence pti was 0.32 and 0.25 for 211At and 213Bi, respectively. For animal B, the tumor mass-weighted average (range) zero-dose fraction F̄0 was 0.31 (0.00–0.54) and 0.25 (0.00–0.46) for 211At and 213Bi, respectively, whereas the pti was 1.0 and 0.94 for 211At and 213Bi, respectively. As predicted, no animals were cured in group B.
Figure 6 compares the estimated average tumor survival fraction S̅F̅ for 211At- and 213Bi-labeled 201B mAb as a function of cumulated activity concentration and corresponding administered activity for animals A and B. The cumulated activity concentration was estimated using the lung residence times for 211At and 213Bi using Equation 14. The resulting administered activities were in accordance with the experimental administered doses used in previous animal experiments—that is, 0.37–3.7 MBq and 0.19–0.37 MBq for 213Bi and 211At, respectively (21). Because of the longer half-life (and residence time) of 211At, the administered activity range was approximately 11 times lower than that for 213Bi. Animals from group A treated with 213Bi-labeled 201B mAb at these dose levels survived longer than those in group B. Histological analysis showed that lung tumor colonies from animals in group A were effectively treated and eradicated in the majority of these animals; however, none of the animals in group B survived. Histological analysis showed that lung tumor colonies continued to grow and form solid tumor masses (Fig. 2). Figure 7 shows the fraction of tumor-free animals as a function of average cumulated activity concentration for animals in group A treated with 213Bi-labeled 201B mAb (21,22) and 211At-labeled 201B mAb (23). Histological analysis of treated animals with optimal doses of 213Bi-labeled 201B mAb showed massive hemorrhage in tumor regions and some surrounding lung, demonstrating loss of tumor integrity (7,21). Even though lung tumors in group A animals were effectively eradicated, histopathology analysis showed that these animals developed lung fibrosis, which was the result of irradiation of normal lung tissue.
DISCUSSION
Although more convenient, the use of α-particle S values is limited in scope and applicability because of its methodologic oversimplification (9–13). S values are problematic because it is difficult to apply them in heterogeneous media, such as air and tissue, and they assume that source-target arrangements are under a uniform activity distribution. Moreover, conventional dosimetry is an arithmetic method that provides an average absorbed dose estimate and it is not descriptive of the intrinsic variability in absorbed dose, survival probability, and overall survival fraction among populations of tumor and normal cells. For short-range radiation such as α-particles, the expectation that increasing cumulated activity concentration or average absorbed dose will lead to a higher probability of tumor control is no longer valid because a fraction of the tumor cells may be completely unaffected. Dosimetry estimates based on S values are not likely to be predictive of the tumor survival outcome in animal models or, more importantly, in clinical trials (3,22,30). An understanding of the variability in absorbed dose and survival probability among all tumor cells is critical for interpretation of α-particle endoradiotherapeutic strategies. Consequently, accurate data describing the morphology of target cells and the spatial activity distribution at the microscopic level are required (14).
We previously introduced the microdosimetry concepts of normalized absorbed dose ẑ and normalized survival probability T̂z0 and their evaluation by means of convolution methods. They were applied to the microdosimetric analysis of antivascular therapies for the treatment of tumors where the endothelial cells were considered to be the critical target cells (22). In this current study, we have extended the same concepts, where the average absorbed dose and the survival probability to a specific target cell are given as z̄ = ẑq and Tz = [T̂z0]q, respectively, and introduced the use of probability density functions, pdf, to express the variability of ẑ and T̂z0 among tumor and normal cells. To simplify the numeric results and to relate the calculated values to the therapeutic effectiveness among all target cells, we divided the area under the curve of the pdf(ẑ) into an under-dose fraction F< (i.e., ẑ < 〈ẑ〉u), an over-dose fraction F> (i.e., ẑ > 〈ẑ〉u), where 〈ẑ〉u was used as threshold, and a zero-dose fraction F0 (i.e., ẑ = 0), which is the fraction of unirradiated tumor cells, regardless of injected administered activity.
The use of the probability density function pdf(ẑ) in microdosimetry is similar in concept to that of a dose-volume histogram in external beam therapy, where the average normalized absorbed dose for a uniform activity distribution 〈ẑ〉u corresponds to 100% of the prescribed external beam dose. The dose-volume fraction with absorbed doses higher than 100% of prescribed dose corresponds to the over-dose fraction F>, and the dose-volume fraction with absorbed doses lower than 100% prescribed dose corresponds to the under-dose fraction F<. These variables provide a simple scheme for the interpretation of experimental results obtained from a given α-particle endoradiotherapeutic strategy.
Finally, using the normalized survival probability density function pdf(T̂z0) from multiple samples, it was possible to assess the average survival fraction S̅F̅ of tumor cells as a function of average cumulated activity concentration q̄. This analytic approach provided an overview, in simple terms, of the dose distribution among target cells for a particular α-particle-targeted radiotherapeutic. We further establish the localized therapeutic inequality as a means of assessing the partition of decay energy between tumor and normal cells. This inequality states that the average normalized absorbed dose and survival probability for tumor tissue must be equal to or higher than that obtained under a uniform activity distribution (CPE conditions), which, in turn, must be higher than that for normal tissue. This inequality can be applied independently of radiation emission type (β- or α-particles) and CPE conditions.
One objective of this study was to apply these microdosimetric methods to analyze the effectiveness of α-particle-emitting 211At and 213Bi-labeled 201B mAb for the treatment of EMT-6 lung tumor colonies in mice. If we had assumed a uniform activity distribution in lung tissue and used a conversion factor or α-particle S value to assess the tumor cell survival probability, the predicted survival fraction SF of lung tumor colonies from both groups of animals would have resulted in complete and effective eradication of all tumor cells. However, this was not the case because none of the animals in group B survived (21). The present microdosimetric analysis based on autoradiography data predicted that 213Bi and 211At could eradicate >99.5% of the tumor cells in animals with relatively small tumors (group A) if adequate activities of radiolabeled mAb were injected (Figs. 5 and 6). These calculations are consistent with prior experimental results: Injected doses of 1–4 MBq of 213Bi-labeled 201B mAb or 0.1–0.4 MBq of 211At-labeled 201B mAb were capable of curing most of these animals. The estimated zero-dose fraction was <0.2% and the probability of tumor incidence pti was predictive of tumor observation after therapy, which was 0.32 and 0.25 for 211At and 213Bi, respectively. In contrast, animals with larger tumors (group B) had an estimated zero-dose fraction between 25% and 30% and a pti of 1.0 and 0.96 for 211At and 213Bi, respectively. These animals were not cured at any tested injected dose, and histological analysis revealed tumors in all of the animals. In the therapy experiments, tumors in these animals showed minimal growth retardation and they eventually progressed to a lethal size.
Attempting to relate the results of these microdosimetry calculations to those obtained in previous radiotherapeutic trials must be done with caution. Although multiple histological images were analyzed for each animal, only 1 animal each was studied by this technique from the groups with similar smaller and larger tumors. Nonetheless, it is encouraging that we showed that the resulting S̅F̅ in lung tumor colonies differed considerably from that obtained assuming a uniform activity distribution and that the average survival fraction S̅F̅ depended on (a) lung and tumor morphology, (b) activity distribution, and (c) α-particle range. Also, the therapeutic effectiveness was inversely proportional to the zero-dose fraction, which was related to the lung tumor colony size.
Tumor cells that were not irradiated in larger tumors were morphologically arranged in large tumor clusters. On the other hand, image analyses of the fraction of untreated tumor cells from animals with smaller tumors showed tumor clusters irregularly arranged throughout the lung tissue with chord lengths measuring <20 μm. A tumor-weighted mean (range) zero-dose fraction F̄0 of 0.0016 (0.0–0.029) and 0.0004 (0.0–0.015) was observed for 211At and 213Bi, respectively. Even though the fraction of unirradiated tumor cells was small, the probability of tumor incidence pti was 0.32 and 0.25 for 211At and 213Bi, respectively. However, histopathological analysis of lung tumor sections of animals with smaller tumors treated with doses of 3.3 and 6.7 MBq of 213Bi-labeled 201B mAb revealed a 0% incidence of lung tumor colonies (22). The estimated spatial uncertainty in these α-particle Monte Carlo calculations, based on image resolution, was approximately 0.5 μm, which was smaller than the measured cluster sizes of unirradiated tumor cells. An explanation of this deviation in tumor incidence could be associated with an immune response. In fact, previous experiments have shown a lower cure rate for immunodeficient SCID mice than for immunocompetent BALB/c female mice, even for small tumors like those in group A (22). Another explanation could be attributed to an α-particle-induced bystander effect, perhaps involving intracellular communication. It is generally believed that the nucleus is the critical site for cell survival where DNA is the essential target for the radiobiologic effects of ionizing radiation. However, recent evidence suggests that bystander effects may also be important in mediating survival of cells not directly hit by an α-particle (31). Experiments have shown the induction of chromosomal instability in the clonal descendants of hemopoietic stem cells after irradiation with α-particles of murine bone marrow (32). Direct evidence has been given for the production of a radiation-induced bystander response in human fibroblasts in non-hit cells neighboring those that were targeted (33). Furthermore, in vivo studies have confirmed that high and low linear-energy transfer radiations induce chromosomal instability in the progeny of unirradiated cells due to unforeseen interactions between irradiated and unirradiated cells, which may have been initiated by the production of free radicals and mediated by gap junctional intercellular communication where the response was likely limited in spatial range (34–36). These effects have relevant implications for mechanistic studies of α-particle radiation action in the eradication of untreated tumor microclusters and micrometastases; thus, the significance of untreated tumor fraction and cluster size are additional critical factors for the correct assessment of tumors survival after α-particle therapy (37).
Even with the simplifying assumptions about the kinetics of radioactivity distribution that were used, our results demonstrate the relevance of the dimensions of tumor morphology at the microscopic level and its role in the selection of a radionuclide for therapeutic purposes. For the specific case of α-emitting radiolabeled mAbs, tumor size was a critical factor dictating model predictions. For small metastases, our results suggest that if the radiotherapeutic distribution is specific and uniform among all cancer cells, then an α-particle-emitting radionuclide should be considered. Alpha-particles are extremely cytotoxic, and only a few nuclear hits are required to inactivate a tumor cell (2). However, to avoid normal tissue toxicity, compounds with a high degree of tumor cell specificity are needed. In the specific example analyzed in this study, α-particles were able to irradiate tumor cell colonies with chord lengths smaller than the range of α-particles (Fig. 4). However, 201B mAb binds to thrombondulin present on murine lung endothelial cells, where it remains bound at the lumenal surface (38). Thus, lung tumor colonies with chord lengths higher than the range of α-particles were ineffectively treated yielding an elevated zero-dose fraction, F0 > 0 (Fig. 5). Moreover, our experience with this model system has shown that surprisingly little acute damage to lung vessels occurred within the administered doses used for treatment. Our experiments demonstrated no endothelial apoptosis or vessel leakiness (or both) in treated lungs. Histological analysis showed that these effects were only significant when administered doses exceeded 7.5 MBq of 213Bi-labeled 201B mAb per animal. However, the administered doses in our experiments were up to 6.4 MBq and 0.4 MBq for 213Bi and 211At, respec-tively. Damage to the lung occurred in the form of pulmo-nary fibrosis, which lead to animal death months after treatment. However, no evidence was observed that endothelial cell damage was involved in this fibrosis. Thus, damage to endothelium was not likely to play a significant role in this therapy strategy.
CONCLUSION
This study presents a new approach for histological image-based microdosimetric analysis and the use of probability density functions pdf for the description of the variability in the normalized absorbed dose ẑ and normalized survival probability T̂z0 in normal and tumor tissues. The methods are a more realistic approach to understanding and comparing the therapeutic effectiveness and limitations of endoradiotherapeutics involving α-particle emitters. This is one step further for the appropriate evaluation of the therapeutic response and overall effectiveness. However, the applicability of these methods is limited by the need to define sites of decay and tumor target-cell geometries at the microscopic level. In this study, this was done using 2D autoradiographs of histological sections and by means of computer-aided image analysis, which was tedious and carried potential systematic errors in image capture, scaling factors, tissue characterization, and reconstruction (15,17,18). Microdosimetry based on autoradiography data could be assisted significantly by the implementation of in vivo technologies that could assess the morphologic characteristics of tissues and the functional distribution of labeled compounds at the microscopic level, which, in turn, may allow following the therapeutic response on a animal-specific basis (39,40). Current techniques in magnetic resonance microscopy can provide lung images with a resolution of 98 μm. With the advent of more powerful MR microscopy technologies, a prospective resolution of 20 μm may be achieved. Nonetheless, these techniques, including micro-CT technologies, require prolonged imaging sessions that may hinder their practical application (40). To summarize, if the practical hurdles can be overcome, microdosimetry based on histological image analysis should be the primary tool to assess, characterize, and compare target radiotherapeutics involving α-particle emitters.
Pharmacokinetic model used to assess residence time in lung tissue. Transfer coefficients λi,j were estimated from uptake and clearance data from previous animal experiments (21). Solution of compartmental model was carried out using algorithm for solving first-order compartmental models involving recycling (29).
Baseline microdosimetry calculations for EMT-6 tumor cells and normal lung tissue cells assuming uniform activity distribution. Estimated cell and nuclear radii for EMT-6 cells were 4.4 and 3.9 μm, respectively, and for normal lung cells were 3.7 and 3.2 μm, respectively. (A) Average survival probability per event 〈T1〉u as function of z0. (B) Average normalized survival probability 〈T̂z0〉u as function of z0. (C) Survival fraction SF as function of cumulated activity concentration q for 211At for cell sensitivity z0 of 0.1 Gy. (D) D0 as function of cell sensitivity z0 for 211At and 213Bi for tumor and normal tissue cells. T̂z=0u represents probability per every unit cumulated activity (MBq s g−1) that cell will receive zero hits under uniform cumulated activity distribution—that is, T̂z=0u = exp[−〈n̂〉u].
Histological images of mouse lungs with EMT-6 tumor colonies (hematoxylin-eosin), where image size was 640 × 480 pixels with magnification of ∼×20, resulting in pixel size of 8.06 μm. (A) Tumor colonies from animal A, 5 d after inoculation, show minimal tumor growth around blood vessels. (B) In contrast, excessive growth of tumor colonies around blood vessels is seen for animal B, 8 d after inoculation. (C) Autoradiography image shows distribution of 125I-labeled 201B mAb in normal lung and tumor colony growing around blood vessel in animal A (arrow). (D) Autoradiography image shows distribution around solid tumor masses in animal B (∼×400; pixel size of 0.41 μm).
(A) Autoradiography image from animal A with lung tumor colonies measuring <100 μm in cross length. (B and C) Probability density function (pdf) for normalized absorbed dose for tumor and normal tissue for 211At (B) and 213Bi (C). Normalized absorbed dose under uniform cumulated activity distribution is given. (D) Survival fraction SF as function of cumulated activity concentration q for cell sensitivity z0 = 0.1 Gy for tumor and normal lung tissue for 211At and 213Bi. Table presents summary of average normalized absorbed dose, tumor and normal tissue CPE ratio, over-dose fraction, under-dose fraction, and zero-dose fraction.
(A) Autoradiography image from animal B with large tumor colonies measuring >400 μm in cross length. (B and C) Probability density function (pdf) for normalized absorbed dose for tumor and normal tissue for 211At (B) and 213Bi (C). (D) Survival fraction SF as function of q for cell sensitivity z0 = 0.5 Gy for tumor and normal tissue for 211At and 213Bi. Table presents summary of average normalized absorbed dose, tumor and normal tissue CPE ratio, over-dose fraction, under-dose fraction, and zero-dose fraction.
Estimated average survival fraction S̅F̅ as function of average cumulated activity concentration q̄ (or administered activity A) for cell sensitivities z0 of 0.05 and 0.50 Gy for animal A and animal B for 211At (A) and 213Bi (B), respectively. Average survival fraction when q̄ → ∞ for animal A was 2.0 × 10−3 and 4.0 × 10−4 for 211At and 213Bi, respectively, and for animal B was 0.23 and 0.18 for 211At and 213Bi, respectively.
Fraction of tumor-free animals in group A treated at different administered doses with 213Bi-labeled 201B mAb (A) (7,21,22) and 211At-labeled 201B mAb (B) (23) 5 d after inoculation with EMT-6 tumor cells. Ratio of tumor-free animals and treated animals is given for each data point. Lungs of treated animals that were free of tumors contained localized foci free of tumor cells, which were presumably irradiated by treatment. Cumulated activity concentration in lung tissue was estimated using Equation 14 and residence time for each radionuclide.
Microdosimetric Analysis for 211At- and 213Bi-Labeled 201B mAb for Animals A and B
Acknowledgments
This work was supported by National Institutes of Health grants CA70164 and CA42324 and by the Department of Energy Office of Biological and Environmental Science through contract ERKP038. The Oak Ridge National Laboratory is managed by UT-Battelle, LLC, for the U.S. Department of Energy under contract DE-AC05-00OR22725.
Footnotes
Received Aug. 29, 2002; revision accepted Dec. 19, 2002.
For correspondence or reprints contact: Gamal Akabani, PhD, Department of Radiology, Duke University Medical Center, Box 3808, Durham, NC 27710.
E-mail: akaba001{at}mc.duke.edu