Abstract
Higher count-rate gamma cameras than are currently used are needed if the technology is to fulfill its promise in positron coincidence imaging, radionuclide therapy dosimetry imaging, and cardiac first-pass imaging. The present single-crystal design coupled with conventional detector electronics and the traditional Anger-positioning algorithm hinder higher count-rate imaging because of the pileup of γ-ray signals in the detector and electronics. At an interaction rate of 2 million events per second, the fraction of nonpileup events is <20% of the total incident events. Hence, the recovery of pileup events can significantly increase the count-rate capability, increase the yield of imaging photons, and minimize image artifacts associated with pileups. A new technology to significantly enhance the performance of gamma cameras in this area is introduced. Methods: We introduce a new electronic design called high-yield-pileup-event-recovery (HYPER) electronics for processing the detector signal in gamma cameras so that the individual γ energies and positions of pileup events, including multiple pileups, can be resolved and recovered despite the mixing of signals. To illustrate the feasibility of the design concept, we have developed a small gamma-camera prototype with the HYPER-Anger electronics. The camera has a 10 × 10 × 1 cm NaI(Tl) crystal with four photomultipliers. Hot-spot and line sources with very high 99mTc activities were imaged. The phantoms were imaged continuously from 60,000 to 3,500,000 counts per second to illustrate the efficacy of the method as a function of counting rates. Results: At 2–3 million events per second, all phantoms were imaged with little distortion, pileup, and dead-time loss. At these counting rates, multiple pileup events (≥3 events piling together) were the predominate occurrences, and the HYPER circuit functioned well to resolve and recover these events. The full width at half maximum of the line-spread function at 3,000,000 counts per second was 1.6 times that at 60,000 counts per second. Conclusion: This feasibility study showed that the HYPER electronic concept works; it can significantly increase the count-rate capability and dose efficiency of gamma cameras. In a larger clinical camera, multiple HYPER-Anger circuits may be implemented to further improve the imaging counting rates that we have shown by multiple times. This technology would facilitate the use of gamma cameras for radionuclide therapy dosimetry imaging, cardiac first-pass imaging, and positron coincidence imaging and the simultaneous acquisition of transmission and emission data using different isotopes with less cross-contamination between transmission and emission data.
As the role of gamma cameras expands in positron coincidence imaging, radionuclide therapy dosimetry imaging, and cardiac first-pass imaging, there is a need to significantly increase the count-rate capability of gamma cameras because of the large photon flux in these procedures. The single-crystal design, the conventional detector electronics, and the traditional Anger-positioning algorithm hinder higher count-rate imaging because of the pileup of signals of the detected events in the detector (1–4). Multiple events may be merged into one artifact event in the detection system; hence, true events are lost while artifact events are generated. This drawback is associated with the involvement of all of the photomultipliers (PMTs) in signal collection for a fixed time period during which scintillation signals from the first event are being generated by the scintillation detector, thereby inhibiting the detection system’s ability to process a second event within this time period. From energy and spatial resolution considerations, a signal collection time of 2–3 τ is preferred, where τ is the scintillation-decay time constant. Because the time lapse between two events is random, the average time lapse between two events should be >10 times the signal collection time (20–30 τ) to keep the probability of signal pileup <10%. For NaI(Tl), this limiting average time lapse would be 5–7 μs, which corresponds to a maximum counting rate of 140–200 kilocounts per second (kcps) per detector head, which has been the maximum counting rate of most gamma cameras for several decades.
Three approaches have been used commercially to increase the camera counting rate. First, a dynamic integration method integrates the first signal until the second signal arrives. An estimated signal supplement is then added to the first event to correct for the signal collection deficit caused by its premature stop in signal integration. The same signal correction is also subtracted from the second event to account for the remnant light from the first event. This method increases the maximum camera counting rate to 350 kcps (5). Second, the delay-line, pulse-clipping method (DLPC) has been used in dedicated NaI(Tl) PET for >15 y (6). The DLPC method electronically clips the exponentially decaying scintillation signal to a maximum width of about τ, so that the signal is integrated only to τ instead of 2–3 τ. This method increases the maximum counting rate by about three times (500–600 kcps). Another advantage of this technique is that it can be easily incorporated into a multizone architecture (dividing the detection area into several pseudo-independent zones) to further increase its count-rate capability. The disadvantage is that all events are clipped and integrated to τ regardless of counting rates, which leads to an overall lower energy and spatial resolution associated with the shorter time integration of scintillation light. Furthermore, if the time lapse to the next event is less than τ, a pileup can still occur. Some newer systems integrate or clip the signals more aggressively to less than τ to achieve higher counting rates, with further sacrifice in energy and spatial resolution. Third, a deconvolution technique with digital signal processors (DSPs) is used in one commercial camera (7,8). Unlike the above two analog techniques, this is a digital technique in which the PMT signals are digitized early. A DSP performs a pulse deconvolution using the inverse transfer function of the pileup signal. The maximum counting rates achieved 300 kcps. The spatial resolution degraded by 28% at the maximum 300 kcps (6).
With these newer techniques, current coincidence cameras can image at higher rates. However, the injected dose of positron tracers for a gamma-camera–based system still must be limited to 37–74 MBq for systems with no slat collimators and 185–370 MBq for systems with slat collimators, instead of the 370–740 MBq for a dedicated PET camera. The lower injected dose further compromises its image quality in addition to its lower detection efficiency compared with a dedicated PET camera. Hence, further increasing the count-rate capabilities of the gamma camera is necessary.
At an interaction rate of 2 million events per second, the fraction of nonpileup events is <20% of the total interaction events, whereas multiple pileups (involving >2 events) are >50% (9). Hence, the recovery of pileup events can significantly increase the yield of imaging photons and minimize image artifacts associated with pileups. We propose a new high-yield-pileup-event-recovery (HYPER) method for processing the detector signal from Anger cameras so that the individual γ energies and positions of pileup events, including multiple pileups, can be recovered.
We first proposed the method for processing the energy signals from scintillation detector probes and showed that the individual γ energies of multiple events can be recovered with good energy resolution. This technique provided a much lower spectral distortion and much higher good counting yield at >2 million cps (9). We further discovered that the HYPER algorithm can be incorporated into the Anger-positioning algorithm to recover the individual position signals in pileups (10) so that, for example, an artifact image count coming from the pileup of multiple events can be converted back to the original counts at their respective positions. It is not necessary to have one channel of the proposed circuit for each PMT, which is a straightforward but costly extension of the single-probe method. We developed a method so that only three channels of HYPER circuits are needed for the whole camera (10–12), whereas a simple nonimaging probe would use one HYPER channel (9). In the camera implementation, one channel of the HYPER circuit is for the X position, one for the Y position, and one for the energy of the events. Hence, implementation of the HYPER electronic algorithm can be simple and cost-effective. To show the feasibility of the design concept and its performance capability, we built a small simple gamma camera with the proposed algorithm and electronics.
MATERIALS AND METHODS
Theory
The basic HYPER-Anger algorithm is briefly summarized here for later reference (9,10). In the Anger-positioning method, assuming that no pileup occurs, the location of the m-th γ-ray is estimated by the centroid calculation:
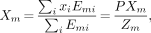Eq. 1
where Emi is the total (integrated) scintillation signal received by PMT i (PMT-i) when the m-th γ-ray is detected, and xi is the physical position of PMT-i. PXm is the prenormalized pseudo-position signal (after signal integration), which needs to be normalized by the total detected (integrated) energy Zm of the m-th γ-ray to generate its centroid location Xm. Note that in the traditional Anger algorithm, all of the variables, Xm, PXm, Emi, and Zm, are not time variables but quantities deriving from the integration of signal over the duration of the scintillation burst.
The above Anger algorithm assumes a special condition where the arrival time of each γ-ray is far apart from other γ-rays (i.e., no pileup). Hence, for each γ-ray, the integration of its exponentially decaying scintillation light is not perturbed by the untimely arrival of the next γ-ray. However, in the general case, an event can be riding on the signals of one or more events (i.e., pileup situations are allowed). This is especially true when the counting rate is >2 million cps, at which rate the majority of the event signals ride on the exponential signal tails of two or more earlier events (9), as shown in Figure 1. It can be shown that for the general case, the prenormalized Anger-position PXm can be expressed as (10):
Eq. 2
where τ is the scintillation-decay time constant of the scintillation detector, and SXm and SYm are given by:
Eq. 3
Illustration of scintillation-crystal signal output in situation of continuous pileups or multiple pileups in high counting rates.
From Equation 2, the prenormalized-position signals PXm and PYm of the current m-th event can be expressed as the difference of a quantity derived from the current event (m) and that of the last event (m − 1) weighted by the exponential time decay between these two events. The significance of this recurring expression is that it depends only on a quantity derived from the current event and the same quantity of the last event, even though the current event may be riding on the pileup signals of many previous events (multiple pileups or continuous pileups). The first term on the right side of Equation 2 is the current (m) gross prenormalized-position signal including all unwanted pileup-position signals. The second term on the right side of Equation 2 is the remnant of the gross prenormalized-position signal of all previous signals (m − 1, m − 2, m − 3, etc.) on which the current (m) net prenormalized-position signal is riding because of pileups. Another important feature of Equation 2 is that it is easy to implement in either analog or digital electronics: It involves only two terms of the same quantity (two consecutive measurements in time) and their time difference. The quantity SXm is the sum of the current instantaneous gross prenormalized-X-position signal (Xm) sampled at the arrival time of the next event (m + 1) and the integral of Xm from the arrival time of the current event to the arrival time of the next event. The instantaneous gross prenormalized-X-position signal (Xm) is the same instantaneous prenormalized-X-position signal (Xm) in a conventional Anger camera. This HYPER-Anger method is valid only for the prenormalized-position signal and not on the energy-normalized position signal. Hence, the energy-normalized position signal (NXm) can be obtained by:
Eq. 4
where Em is the total energy deposition of the m-th γ-ray. Because the detected energy deposition of the γ-ray also should be free of the pileup effect, Em is also measured with the HYPER algorithm electronics:
Eq. 5
where Sm is the total gross energy stored in the detector immediately after the interaction of the m-th γ-ray. Sm includes the leftover energies from all previous γ-rays (m − 1, m − 2, m − 3, etc.), and the second term is leftover energies from all previous γ-rays (m − 1, m − 2, m − 3, etc.). Hence, Em is the net energy of the m-th γ-ray. Again, similar to Equations 2 and 3, the total gross energy stored in the detector immediately after the interaction of the m-th γ-ray is given by (9):
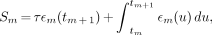Eq. 6
where εm(tm+1) is the instantaneous gross energy signal of the detector just before the next γ-ray (m + 1) hits the detector.
Because the mathematic formalisms for the energy and the X- and Y-prenormalized positions are identical, the same electronic circuit design can be used. Hence, three identical channels of HYPER electronics are used in this method for a gamma camera. To illustrate the theoretic validity, engineering feasibility, and performance capability of the new method and to develop the physics and engineering technology needed, a minimal gamma camera was developed.
Small Gamma Camera with HYPER-Anger Electronics
The minimal camera has a NaI(Tl) crystal with four PMTs. The NaI(Tl) crystal is 10 × 10 × 1.0 cm, and it is coupled to four R1534 PMTs (5.1 cm2) (Hamamatsu, Hamamatsu City, Japan). The four sides of the crystal are painted black to avoid light bouncing from the side walls back to the central portion of the crystal. For such a small-area gamma-camera crystal, the black paint is necessary to control this stray light from significantly degrading the position decoding accuracy because, compared with a large clinical camera crystal of the same thickness, this side-wall effect is much more significant. The black paint combined with the medium quality of the inexpensive crystal degraded the energy resolution to 11.5%–12% (measured with conventional electron-ics) from the typical 9%–10%. Because the gamma camera was designed to be exposed to very high γ-ray flux, with all scintillation light channeled into only four PMTs, the signal-current load of the PMT high-voltage dividers will be very high. This high load would cause high-voltage fluctuation in the high-voltage dividers, which in turn would cause gain fluctuation in the PMT, unless a very high bias-current divider is used. A special high-voltage divider using two power supplies was designed for the PMT; it passes a very high biasing current for the last three PMT dynodes and a much lower biasing current for the earlier dynodes to avoid overheating associated with a conventional high-current design. The PMTs were also biased with negative high voltage (1,200 V) to avoid signal direct-current (DC) baseline drifts at very high counting rates; otherwise, the energy resolution, photopeak energy, and event localization would be unstable. The small camera is enclosed in a light-tight aluminum can. Because the camera is used only for electronic development and for illustrating the validity of the HYPER concept, this simple camera lacked the normal corrections such as linearity and energy correction. Hence, there were some pin-cushion distortions.
A HYPER-Anger algorithm was implemented in electronic circuits. The electronic architecture implementing Equations 2–6 is shown in Figure 2. It has three identical channels of HYPER circuits, one each for the X and Y positions and one for energy deposition. Each HYPER channel uses an analog-to-digital converter (ADC) chip with dual 8-bit ADCs (internally temperature balanced) to minimize electronic dead time. There were also two channels of integrators in each HYPER circuit; each of these dual integrators is connected to the partner of a dual ADC. Whereas one integrator and its associated ADC is serving the current event, the complementary partner integrator and ADC, which served the last event, will be discharging the signal of the last event so that it can be prepared for the next. This ping-pong integrator and ADC design has minimal electronic dead time, which is essential for this high count-rate camera. The input to the X and Y channels is from a regular resistor-divider network (for PMT position weighting) as used in most gamma cameras. All PMT outputs were also summed into the energy channel. As a current event (m) reaches the HYPER circuit, the signal is distributed to two branches, an instantaneous channel and a parallel integration channel, which starts to integrate the current instantaneous signal. The results of these two branches are then summed continuously for implementing Equations 3 and 6. At the detection of the arrival of the next event (m + 1), the integration is stopped and the sum is converted by the ADC into a digital quantity and stored in a temporary register (SXm in Eqs. 2 and 3). SXm will be combined with the previous quantity SXm−1 (also stored in a temporary register) according to Equation 2 to derive the final prenormalized-position PXm for the current event. This recurring process is continued for the next event. The prenormalized X and Y positions are then normalized by the energy from the E channel to generate the real-position signal Xm and Ym for the current event. These final-position signals Xm and Ym are then passed to a high-speed data acquisition system designed for a personal computer. The final HYPER-Anger electronic circuit is very simple and compact. Because this circuit works on the prenormalized-position signals that exist in regular cameras, the same circuit can be used for a much larger clinical camera replacing the regular integrator/ADC circuit board. Hence, the proposed HYPER electronic design does not add much to the complexity, space requirement, and production cost of a clinical camera.
Schematic architecture of HYPER-Anger electronics. ADC = analog-to-digital converter; MUX = multiplexer; FIFO = first-in first-out memory buffer.
RESULTS
The energy resolution and imaging aspects of the camera were tested for a wide range of activities ranging from 60 to 3,500 kcps. Hot-spot and line sources with very high 99mTc activities were imaged. A custom-made, parallel-hole collimator (2.5 cm deep) was fitted to the small 10 × 10 × 1 cm NaI(Tl) crystal of the camera.
Energy Resolution
Energy resolution using the proposed technique was measured with a small point source of 99mTc for a wide range of counting rates. The pulse-height spectra are shown in Figure 3. At 2,000–3,500 kcps, a small amount of 2-γ pileups leaked through the HYPER circuit. However, because the photopeaks were still preserved at these very high counting rates, most of this small pileup leakage can be easily discriminated by the upper threshold of the energy window. The measured energy resolution as a function of counting rates is shown in Figure 4. The energy resolution (full width at half maximum [FWHM]) was found to be 13% at 600 kcps, 15% at 2,000 kcps, and 19% at 3,500 kcps. At a low counting rate (50 kcps), the energy resolution was 11.5%–12% because of the black paint on the side wall and the quality of the crystal, as described. The measured energy resolution degraded as counting rates increased, as expected. Most of the degradation was associated with the increasingly shorter integration time for each event as the mean time of arrival between events was shortened with higher counting rates. We have also calculated the ideal resolution degradation as a function of counting rate; this calculation assumed that every event came in a fixed time interval equal to the reciprocal of the counting rates, the signal integration time was equal to the fixed time lapse between events, and the remnant signal disappeared or was clipped right after the integration so there would be no pileup for the next event. The ideal calculation is also shown in Figure 4 for comparison. The ideal case cannot exist in nature because events arrive randomly. This ideal, yet unreal, case had no pileups and optimally integrated all signal to the fullest extent allowed at a given counting rate; it represented the ideal limit of resolution degradation as the counting rate increased. From Figure 4, the measured energy resolution was quite close to the ideal case at counting rates <3 million cps. Hence, for energy resolution, the HYPER algorithm and electronics are close to ideal or optimal below 2–3 million cps at the present stage of development. The shifts in photopeaks (Fig. 4) are <3% up to 2 million cps, and the shift increases to 6% at 3.5 million cps. Hence, one tight energy window can accommodate up to 2 million cps, whereas a wider energy window may accommodate 3 million cps at the present state of development. The next step is to illustrate the concept of HYPER on imaging or position decoding.
99mTc energy spectra of gamma camera as function of counting rates.
Measured and ideal energy resolution as function of 99mTc counting rates.
Images of Nonpileup and Pileup Events (Four-Hot-Spot Phantom)
A phantom with four hot spots placed diagonally was imaged. The point sources were just four circular holes drilled into a 5.1-cm (2 inch) lead brick. Each hot spot has the same size (3.5-mm diameter) and approximately the same radioactivity level (±10%). The purpose of this phantom study was to image nonpileup events and purely pileup events to illustrate the manifestation of pileup artifacts. For this study, the triggering circuit was detuned so that it failed to recognize more pileup events. With more pileup leaking through the system, there was a definite 2-γ–pileup peak (two times the photopeak energy) and a 3-γ–pileup peak (three times the photopeak energy) above the regular photopeak. We set up an energy window to select only events corresponding to 2-γ–pileup events (unrecovered) and 3-γ–pileup events (unrecovered). The recovered-event image is from the regular operating mode of the HYPER electronics using a photopeak window.
The images of these three event types for the four-point phantom at 2 million cps are displayed in Figure 5. At 2 million cps, the recovered-event image preserved the image of the four hot spots without the artifacts of pileup (Fig. 5A). The two upper points show some slight elliptic distortion, which is associated mainly with the lack of linear correction in this simple concept-demonstrating camera. The 2-γ–pileup image is an artifact image made up of primarily 2-γ–pileup events, and the 3-γ–pileup image is also an artifact image. From Figure 5B, four true point sources created image artifacts of nine circular spots caused by 2-γ pileups. The four corner artifacts (COAs) were caused by two events coming from the same point source. The four side-middle artifacts (SMAs) were caused by two γ-rays from the two point sources on the same side. The center artifacts (CEAs) were caused by the two diagonal pairs of point sources. The relative image-artifact intensity (density) ratio of COA:SMA:CEA was 1:2.1:4; which agreed with the expected probability of 1:2:4.
Images of four-hot-spot phantom (99mTc). (A) Pileup recovered image using HYPER circuit at 2 million cps. (B) Image artifacts caused by pileup of two γ- rays. (C) Image artifacts caused by pileup of three γ-rays.
The 3-γ pileup generated 16 image artifacts with very high pileup artifacts in the central region of the image. With two artifact patterns established by Figures 5B and C, we can compare the artifacts to the pileup-recovered image of the system (Fig. 5A). In the recovered-event image, there is no visible sign of 2-γ– and 3-γ–pileup artifacts. The central region of the image would have been particularly sensitive to 2-γ and 3-γ pileups as observed from Figures 5B and C. This phantom study showed two of the artifact patterns produced by pileups and the validity and pileup-recovering capability of the HYPER-Anger method. From Poisson probability calculation, at 2 million cps, the 2-γ and 3-γ pileup (combined) would have been four times more common than the nonpileup events (9).
Line-Source Phantom
A line source (2-mm width, 99mTc) was imaged at different counting rates from 60 to 3,000 kcps. This was to study line-spread-function (LSF) degradation as a function of counting rates. The relative FWHM and full width at tenth maximum (FWTM) of the line were measured. The result is shown in Figure 6A and Table 1. The FWHM widened as counting rates increased, as expected. At 3,000 kcps, the FWHM increased to 1.6 times that of 60 kcps. The FWTM were generally two times that of the FWHM, and the increased counting rates did not change this ratio (Table 1). Hence, the HYPER recovered image did not excessively degrade the tail characteristic of the LSF. The FWHM and FWTM widening at high counting rates were partially caused by the increasingly shorter integration time for each event as the mean time of arrival between events was shortened with higher counting rates. At 1,000 kcps, the mean arrival time between two events was 1,000 ns, and at 3,000 kcps, the mean arrival time between events was 330 ns. Hence, the signal integration time decreased by a factor of 3 from 1,000 to 3,000 kcps, which implies that the amount of light collected at 1,000 kcps is 30% more than that collected at 3,000 kcps. Because spatial resolution depends approximately on (light output)1/2 in ideal situations (13), the FWHM should ideally increase by about 14% between 1,000 and 3,000 kcps. In our imaging measurement (Table 1), the FWHM increased by 21% between 1,000 and 3,000 kcps. Hence, the shorter average integration time, as required by physics, accounts for two thirds of the broadening of FWHM. The other contribution to the width broadening may be the imperfection of this first-generation HYPER electronics. Other than FWHM widening, no other imaging artifacts were observed in this isolated line source. The ideal case of resolution degradation as a function of counting rates was also calculated. The ideal case, whose assumptions are similar to those in the energy resolution section, assumed that all events came in a regular time interval so that a fixed shortened integration time can be used at each counting rate. We also assumed that the scintillation signal is totally clipped just before the onset of the next event so that there is no remnant signal on which the next event can pile up. Certainly, the ideal case cannot exist in nature, but it provided the idealistic limit for count-rate performance. The ideal calculation is based on the FWHM at 60 kcps and that spatial resolution is proportional to the square root of the amount of light collected with the integration period allowed by a given counting rate. From Table 1, the HYPER-Anger electronics deviated from the ideal resolution by 30%–40% for 1,000–3,000 kcps, at least with this first-generation prototype electronics. This spatial resolution deviation is larger than that of the energy resolution shown above. With more electronic design refinement on the spatial circuit, this spatial resolution deviation may be reduced.
(A) Image LSFs measured by isolated line source (99mTc) from low to high counting rates. (B) Energy pulse-height spectra and images of line- and point-source phantom (99mTc) at different counting rates.
LSF Widths (FWHM) at Different Counting Rates
Line- and Point-Source Phantom
A line source (2-mm width) surrounded by six point sources (3-mm diameter) was imaged. The objective of the study was to look for image artifacts and degradation in LSF FWHM in a severe pileup condition. Both the line and the point sources were filled with approximately the same activity density of 99mTc (±15%). Images were acquired with the camera from 60 to 2,700 kcps. The images and energy pulse-height spectra are shown in Figure 6B. The point sources on either side of the line were for generating localized pileup near the line, especially on the central sections of the line that received pileups from both the four diagonal point sources and the two point sources on either side (Figs. 5B and C). No image artifacts were observed on the central region of the line. The width of the line increased uniformly along the line with increasing counting rates, as expected. The line width as a function of counting rates is shown in Table 2. At 2,000 kcps, the line width was two times that at 60 kcps. In this configuration, the line width increased more with counting rates than that of an isolated line (Fig. 6A), which was expected. Above 1,000 kcps, the FWHM was 45% wider than that of an isolated line. However, the images were still free of 2-γ–pileup and 3-γ–pileup artifacts (Figs. 5B and C) and had only minor distortions at 2,300 kcps for this demanding configuration and counting rate. Some of the elliptic distortion of point sources was caused by the lack of corrections in this simple camera; even at low counting rates there was some elliptic distortion for the point sources at the four corners.
LSF Widths (FWHM) for Source of One Line with Six Points at Different Counting Rates
The pulse-height spectrum was also usable at 2,300 kcps because there was a distinct photopeak where a meaningful energy window can be set. To illustrate the importance of subtracting the signal remnant of previous events (the second term on the right side of Eqs. 2 and 5), energy spectra and images were acquired with and without this remnant subtraction at 2,000 kcps (Fig. 7). The data were acquired by the HYPER-Anger electronics with the dynamic integration circuit activated but with the remnant subtraction circuit disabled. Without the remnant subtraction, there were severe distortions in both the energy spectrum and the image because of scintillation-remnant pileup.
(A) Energy spectrum and image with signal-remnant subtraction activated. (B) Energy spectrum and image without signal-remnant subtraction. Data were acquired with line and point source for 99mTc at 2 × 106 cps.
DISCUSSION
We have proposed a new HYPER method for processing the detector signal from Anger cameras, so that the individual γ energies and positions of pileup events, including multiple pileups, can be recovered. This signal-processing algorithm was developed into the electronics of a minimal gamma camera for validation and performance demonstration. This camera showed that the proposed HYPER-Anger theory is valid and technically feasible and that the circuit complexity (space and cost) is on par with that of a regular gamma camera. The camera further showed that the energy pulse-height spectrum was useful up to 3 million cps and that artifact-free imaging can be achieved for 2–3 million cps. Although this concept-demonstration experiment was performed with 99mTc and not 18F, the count-rate capability of the HYPER electronics for 18F is expected to be similar or better. If 18F were used, the amplifier gain would be adjusted down by the fraction 140/511 to account for the energy difference; the PMT signal of 18F would then look like that of 99mTc and the HYPER circuit would process both signals the same way. Because 18F has better energy resolution than 99mTc, the energy window can be set narrower. This narrower 18F window will further reject more leaking-through pileup events than that of 99mTc. Hence, we expect the HYPER performance for 18F to be similar or better. For the present state of development with the first-generation HYPER-Anger electronics, the FWHM of the LSF increased by 60% at 3 million cps (from 60 kcps), which is 40% wider than is the ideal LSF FWHM. At 1 million cps, the FWHM degraded by 31%, which is comparable with the 28% degradation at the lower rate of 300,000 cps for the pulse deconvolution method (7). With further electronic design improvement, this increase in LSF FWHM may be reduced. Improvements can be made in two areas. The first area is to design a lower noise front-end amplifier circuit and lower noise discriminator trigger for detecting more accurately the onset of the next event, especially for the lower energy scatter events. The second area is a faster discharging circuit for the integrator. The present circuit takes 25 ns to fully discharge the integrator. This 25-ns time is the limiting dead time for the HYPER circuit. We have recently developed a 3-ns discharging circuit, but it has not been implemented into the HYPER electronics used for this study.
If the proposed method is to be implemented in a clinical gamma camera with many more PMTs, the camera (or PMTs) can be split into multiple independent regional zones. Each zone can have its own HYPER-Anger electronics. For example, a four-zone HYPER-Anger system, with each zone operating at 2 million cps, may accommodate up to 8 million cps. However, some of the events occurring near the borders of two adjacent zones will cause double triggering in two zones, which reduces the effective counting rates from the idealistic limit of 8 million cps. From the typical 5.1- to 7.6-cm (2–3 inch) PMT size used in the current gamma camera, we estimated that there is a 25% cross-triggering that would reduce the effective counting rate to about 5–6 million cps. If each zone can operate up to 3 million cps individually, a four-zone system may operate to 9 million cps, which would be useful for positron coincidence imaging, radionuclide therapy dosimetry imaging, and cardiac first-pass imaging.
Another potential application is the simultaneous acquisition of transmission and emission data, which uses different isotopes for performing attenuation correction for the emission data. In this scheme, a lower energy isotope is used for the transmission data to avoid the contamination of emission data by the transmission source. On the other hand, a very active transmission source (e.g., 10 times relative to emission counts) can be used so that the fractional cross-contamination coming from the scattered emission events into the transmission data can be reduced proportionally. However, this scheme, which generates more accurate emission and transmission data simultaneously, may require a very high counting-rate gamma camera to handle the very high transmission data rate.
CONCLUSION
We have introduced a new HYPER method for processing the detector signal from Anger cameras, so that the individual γ energies and positions of pileup events, including multiple pileups, can be recovered. In this study, this method was tested in a gamma camera for validation, feasibility, and performance demonstration. This study showed that the proposed HYPER-Anger theory is valid and technically feasible and that the circuit complexity (space and cost) is on par with that of a regular gamma camera. The study further showed that the energy pulse-height spectrum was useful up to 3 million cps and that artifact-free imaging can be achieved for 2–3 million cps. In conclusion, this study showed that the HYPER electronic concept works; it can significantly increase the count-rate capability and dose efficiency of gamma cameras. In a larger clinical camera, multiple HYPER-Anger circuits may be implemented to further improve the imaging counting rates that we have shown by multiple times. This technology would facilitate the use of gamma cameras for radionuclide therapy dosimetry imaging, cardiac first-pass imaging, positron coincidence imaging, and the simultaneous acquisition of transmission and emission data using different isotopes with less cross-contamination between transmission and emission data.
Acknowledgments
This work was supported in part by the National Institutes of Health (Public Health Service grants RO1 CA76246, RO1 CA61880, and RO1 CA58980), the J.S. Dunn Research Foundation, the Cobb Endowment for Cancer Research, and the 1999 Radiological Society of North America Education and Research Seed Grants.
Footnotes
Received Mar. 27, 2000; revision accepted Aug. 14, 2000.
For correspondence or reprints contact: Wai-Hoi Wong, PhD, Department of Nuclear Medicine, The University of Texas M.D. Anderson Cancer Center, Box 217, 1100 Holcombe Blvd., Houston, TX 77030.
In this issue
Jump to section
Related Articles
Cited By...
- Engineering and Performance (NEMA and Animal) of a Lower-Cost Higher-Resolution Animal PET/CT Scanner Using Photomultiplier-Quadrant-Sharing Detectors
- Performance Evaluation of the FLEX Triumph X-PET Scanner Using the National Electrical Manufacturers Association NU-4 Standards
- New Developments in PET Instrumentation: Quo Vadis PET?
- Merging the Instrumentation Evolution