Abstract
A meta-analysis of data primarily from PET oncologic investigations using FDG PET was performed. Its purpose was to establish statistical features of the distributions of standardized uptake values (SUVs) as possible aids in the diagnostic process. Methods: We obtained 1536 values of oncologic markers from patient studies of 40 investigations in the literature. Statistical parameters were tabulated for analysis. Results: A significant observation is that, unlike skewed SUV histograms, log10SUV has Gaussian behavior, which is not uncommon for biologic quantities. This was found for SUVs of FDG and 2 amino acids as well as a few other cancer markers. A possible model for explaining this is proposed. For FDG, the SD σ of the log10SUVs for an average cancer category was 0.23. Examining data within the framework of the model points to physiologic factors as dominating SUV variability rather than PET protocols. When data for a single cancer category were available from multiple institutions, averages, S̅U̅V̅s, disagree beyond chance expectations. Diagnostic utility suggestions include a universal linear relationship between sensitivity and severity, defined as SUV/S̅U̅V̅, on semilogarithmic probability paper; a generic receiver-operating-characteristic curve for all cancers; using [log10(S̅U̅V̅mal/S̅U̅V̅norm)] ÷ (σmal2 + σnorm2)1/2 as a simple diagnostic effectiveness measure; and using Gaussian log10SUVs to avoid erroneous P values. Conclusion: Using the logarithms of markers, such as SUVs, several advantages stemming from their Gaussian nature can be achieved with benefits ensuing to the diagnostic process.
Presently, FDG is the most popular tracer in PET oncology. This stems from tumor metabolism being characterized by enhanced glycolysis compared with normal or benign tissue. A frequently used quantitative aid is the standardized uptake value (SUV), which is basically the ratio of 2 specific activities: that of a tumor at the study's end and a temporally constant entire body average. Its clinical appeal, compared with various other quantitative approaches, lies in its simplicity. Thus, the SUV is very commonly used as an adjunct to visual interpretations. Not surprisingly, an overwhelming volume of SUV data has accrued in PET oncologic literature.
An underlying premise of this investigation is that the application of statistical information contained in SUV data might improve diagnostic usage of the latter. Statistical models have been applied (1–3) to cerebral glucose metabolism and blood flow with analogous motives. That oncologic diagnostic methods might benefit from a statistical study of SUVs stems from a basic principle that the mean values, S̅U̅V̅s, and shapes of overlapping benign or normal and malignant SUV distributions (i.e., histograms) directly determine a study's sensitivity and specificity (4). The S̅U̅V̅ ± SD is universally reported for patient subgroups. However, research on distribution shape and its influences on the underlying performance of the FDG protocol is essentially nonexistent. A rare exception is the research of Ponto et al. (5), who showed histograms of normal liver, spinal vertebrae, and thyroid FDG SUVs; however, those data were summarized as means ± SD for further use. An investigator, recognizing that the SUVs skew toward high values, might, on rare occasions, report a median rather than a mean. However, the consequences of this shape have been ignored. In t testing, ANOVA, Pearson correlations, and so forth, failure to recognize the skewed distributions that violate Gaussian assumptions can possibly lead to incorrect conclusions.
Besides documenting SUV distribution features extracted from data in FDG literature, we have searched for practical applications of these in diagnoses and for insights offered: These include addressing underlying phenomena responsible for distribution features. This has yet to be confronted even though reducing distribution widths (i.e., data variabilities) would have an immediate payoff in terms of improved sensitivity and specificity.
In many facets of biology, research has been directed toward statistical distributions. A not uncommon result in many investigations came from the logarithms of observable biologic quantities. These, rather than the quantities themselves, exhibited nature's ever-prevailing Gaussian (or normal)histogram shape (6). Prominent among explanations for this is the law of proportionate effects involving randomness in multiplicative factors occurring in a process (Appendix). A few examples of lognormal behavior among numerous ones in the literature are doubling times of cancers, sizes and weights of species, sensitivities to drugs, tumor sizes, and cell geometric quantities including cell density in tumors. Taking this cue from others, our work therefore examines the consequences of hypothesizing a lognormal distribution for the SUVs—that is, testing log10SUV data for a Gaussian shape.
MATERIALS AND METHODS
A well-planned, multicenter prospective investigation would be the ideal approach for obtaining the SUV data. However, many patients would be required. Therefore, as an initial exploration that can give immediate results, a compromise approach was to use meta-analysis (7). With this technique, SUV distribution data were examined retrospectively in each of many separate historical investigations. Its limitations must be recognized (8). For example, discussions of patient population characteristics below point out some issues.
An oncology database that was created required defining acceptance criteria. The database emphasized primarily the SUVs of malignant lesions in FDG PET. It sought variety in cancer categories and institutions studying these, provided there were sufficient numbers of lesions in each investigation:
From an investigation, n ≥ 20 lesion or normal tissue quantifiers, with these obtained from a minimum of 13 (human) patients
Reported individual quantifier values identifiable in a tabulation or graph
Exclusion of studies that monitor the effects of treatment
Investigations appearing in English language publications since 1987
Accepting the investigator's defined patient population and classification of cancer studies, but not having metastases from a particular type mixed into a category having other types. The investigator's policy on whether to exclude diabetics was also accepted.
Most investigations included scans of only untreated patients. Otherwise, months between treatment and scanning would be typical. Ideally, classifications might be based on the many discrete classes from histology. Unfortunately, if these were used the number of available published investigations would be substantially reduced, and this would often lead to subgroups having too few patients for statistical analyses. Hence, cancer classifications of investigators were adopted here.
For purposes of some limited comparison with FDG SUVs, data from 2 amino acid PET tracers as well as cancer markers from CT, tumor volume, and DNA were included. The SUVs from a few investigations of normal tissues were also examined. Unfortunately, publication bias (investigators more prone to publish tumor data) discriminates against having more normal tissues represented.
For each investigation, there was a tabulation of its quantitative marker—usually SUV—with the postinjection time for its evaluation noted. These markers provided the input information to spreadsheet (Lotus 1-2-3. Cambridge, MA: Lotus Development Corp.; 1989) and statistical (Statistica. Tulsa, OK: StatSoft, Inc.; 1997)software. Only in one sixth of the PET investigations were there corrections involving the partial-volume effect, plasma glucose concentration, and body fat content. One fifth of the FDG investigations were conducted with diabetics excluded; in all others, only a few cases of abnormally high glucose were reported.
Popular quantifiers of distributions were calculated. Other specific statistical measures were Lilliefors implementation of the Kolmogorov-Smirnov goodness-of-fit test for Gaussian behavior, Kruskal-Wallis analysis of variance by ranks, and Bartlett's test for equality of variances.
RESULTS
Using the SUV data of Delbeke et al. (9) as typical, Figure 1 shows the tendency of the histogram to be positively skewed (i.e., toward higher values). Such histograms are characterized by 3 parameters: mean, SD, and skew (Appendix, skew formulae). On the other hand, the log10SUV histogram of these data is symmetric and would be well characterized by just SD σ and mean. Tables 1 and 2 summarize the statistical findings of this meta-analysis. For example, the data of Figure 1 were used in calculations for one of the rows in Table 1. A result showing indications of how logarithms reduce and remove the positive skew may be found in the columns of skew ÷ its measurement SE. The 2.9 average of this quantity for SUVs from 25 FDG tumor investigations was rather high; the average was only 0.3 for log10SUVs.
Statistical Features of FDG PET for Various Cancer Categories and Some Normal Tissues
Statistical Features of Some Representative Amino Acid PET SUVs and Other Cancer Markers
Although histogram presentations are the more common, a plot of the type in Figure 2 better facilitates visualizing whether distributions have a Gaussian character. In such plots, Gaussians are straight lines (Appendix). This composite of all investigations shows such behavior. By using SUV/S̅U̅V̅ as an index of severity, diverse cancer types can be compared. The average σ̅ = 0.23 from Table 1 has its reciprocal defining the well-fitting slope shown. However, for a more stringent test of the hypothesis that log10SUVs are Gaussian, whereas SUVs are not, P values of the Lilliefors-Kolmogorov-Smirnov test were used. In Tables 1 and 2, a low criterion (P < 0.01 for non-Gaussian occurring by chance) was used in assigning Gaussian or non-Gaussian distribution because of many investigations analyzed simultaneously. For all investigations of malignancies in Tables 1 and 2, almost half of the SUVs failed to fit a Gaussian distribution, whereas the log10SUV failed in only 1 investigation.
Diagnostic sensitivity for 921 malignant lesions from 25 FDG investigations of various cancer categories. Commonality seen here stems from Gaussian probability axis used in combination with severity, SUV/S̅U̅V̅, expressed on logarithmic scale. Slope of fitting line is related to average 0.23 SD of log10SUVs for all cancer types in Table 1.
The σs in Tables 1 and 2 can be examined statistically for possible evidence of any commonality among the various categories. For example, even SUVs of normal tissues and the 2 amino acids' scans show σs not too far from those of FDG in tumors. Table 1 data show that 68% of the coefficients of variation (CVs) of SUVs are within ±0.14 of their average 0.55. Correspondingly, 68% of the σs are within ±0.05 of their average 0.23. However, in spite of these similarities, Bartlett's test of the 25 investigations making up this latter result showed that these do not all have statistically equal variances σi2 (P < 0.001)—that is, differences among the categories are significant. Thus, no overall commonality was detectable from the σs. However, within a certain type of investigation, as an inspection of non-Hodgkin's lymphoma or breast cancer σs shows, it may be that a common σ could exist.
In 4 of the FDG investigations the average number of lesions per patient exceeds 1.5. As 1 type of assessment of any multiple lesion effect, where data were available, calculations were also performed with a patient's multiple lesions replaced by just a single lesion with an average SUV. In no instance did this have more than a 1.05 factor effect on an investigation's CV.
The average time of evaluations for FDG SUVs in tumor studies was 57 min, with a SD of 8.5 min. This leads to variability associated with the rising SUV(t). Results of a simple theory (10), based on population SUV(t) of several cancers, gives (d[SUV]/dt)57 min × (8.5 min)/(average SUV) ≈ 0.035. This, on average, is the small CV effect attributable to ±8.5-min evaluation time variations.
Other data at the bottom of Table 1 and in Table 2 supplement that of FDG SUVs for tumors. These data also exhibited lognormal behavior. This tends to suggest a wide occurrence of this distribution among markers. The few data from modalities other than PET, with considerable variety in their methods and tissues, showed more scatter in the σ values tabulated—that is, more than the 0.11–0.32 range from FDG SUVs in tumors.
DISCUSSION
Data Features
Many investigations have taken place encompassing various cancer categories and involving the popular FDG tracer of PET. A small subset of these met our criteria for inclusion in Table 1. For this subset, additional distribution characteristics of results—especially information beyond the S̅U̅V̅ ± SD typically reported—have been calculated from published data.
A somewhat subjective ranking, in a decreasing importance order, for a distribution might be the mean, SD, and skew. The CVs are preferred to SUV SDs. Being normalized, the CVs' range of values among cancer categories was consequently more restricted than that of wide-ranging SUV SDs. Similarly, a more-or-less restricted range was found for the log10SUVs' σ, as the latter is essentially the SUV CV ÷ 2.303 (Appendix). Nevertheless, statistical testing showed no commonality among σs of the different cancer types.
Tables 1 and 2 show that the logarithm operation on SUVs tended on average to remove skew. Moreover, the small positive and negative skews were equally likely for log10SUV. On the other hand, SUV distributions always showed positive skews. For log10SUVs, the largest ratio of skew to its SE found in a total of 40 investigations in Tables 1 and 2 was only 2.3. This skew removal is associated with the functional nature of taking a logarithm: compressing values, with larger ones causing the skew in SUVs being compressed more.
The global cerebral glucose metabolic rate is not in Table 1 because it is well reviewed elsewhere(11,12). This is closely related to the SUV. Thus, its statistical behavior might be compared with findings from Table 1. A review by Wang et al. (11)provided data for compiling Table 3: The data from multiple investigations of normal brain tissue were examined further in the manner of Table 1. Normal brain tissue shows a significantly smaller FDG σ̅ than all tumor types. The many factors influencing cerebral glucose uptake have been well studied and understood (11,12). Presumably aware of and accounting for these, investigators have been able to obtain a more-or-less intrinsic constancy in brain tissues' uptake in a well-defined population. Also, for both cancers and normal brain, the spread of the σs is about twice that expected from a hypothetic circumstance of all investigations assumed to have the same intrinsic variance of their σs. This corroborates Bartlett's test result, which indicated a lack of homogeneity among categories in Table 1.
Comparison of Selected Statistics of FDG Uptake in Cancer Lesions (from SUVs) and in Normal Brain Tissue (from Metabolic Rates)
Another question to examine is whether variations among S̅U̅V̅s in Table 1 (even factors of 2 or more) from investigations involving the same cancer category have statistical significance. This would show whether these have sufficient similarity in patient populations and PET protocols, including types of corrections (1,12–14) made. Within several categories (non-Hodgkin's lymphoma, breast, head and neck, and pancreatic cancers as well as normal liver), the Kruskal-Wallis P for the reported discordant results to be occurring by chance was always <0.0001. Thus, for a given category, 1 or more among its 3 or 4 investigations reported presumably had significantly different patient or protocol (or both) characteristics. Until there is better understanding, interinstitutional comparisons must evidently be made with caution.
Theoretic Reasons for Lognormal Distribution
Gaussian distributions fitting log10SUVs is a significant observation. A variable with this type of distribution that is found so frequently in nature might be regarded as a more natural marker than a distribution that is non-Gaussian. However, because of limitations from available numbers of lesions or patients for a distribution, it has not been uniquely determined that the logarithm, rather than some other function, is best. Hence, the empiric evidence favoring logarithmic usage might be supplemented with some theoretic points.
There are underlying factors responsible for observed SUV variabilities in a given institution's investigation of a single cancer category, using the individual locally standardized procedures. A review by Carson (15) shows that these factors are attributed to separate influences: fundamental physiologic, test measurement, and data analysis. One approach is to express the observed SUV approximately as a product of factors, all of which contain their own internal sources of variability. This extends and quantifies a proposal by Bland and Altman (16) that rate constant products can lead to lognormal distributions:



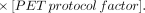 The first factor is the Gjedde-Patlak accumulation rate K. It and the second factor approximate the patient's intrinsic SUV in terms of basic physiologic quantities (17). Equation 1 contains the rate constants of the model of Sokoloff et al. (18). Here the product, PS, of capillary permeability P and its surface area per gram S is an explicit replacement of this model's rate constant k1. V is an entire body distribution volume associated with a tracer plasma clearance rate kp.
The first factor is the Gjedde-Patlak accumulation rate K. It and the second factor approximate the patient's intrinsic SUV in terms of basic physiologic quantities (17). Equation 1 contains the rate constants of the model of Sokoloff et al. (18). Here the product, PS, of capillary permeability P and its surface area per gram S is an explicit replacement of this model's rate constant k1. V is an entire body distribution volume associated with a tracer plasma clearance rate kp.
The PET protocol factor is a calibration factor, defined as the ratio of measured SUV to intrinsic SUV. It is the product of many (measured ÷ true) factors originating from many variability sources (1,12–14). These include counting statistics and corrections not fully made in interpreting the SUV measuring process. In particular, the absence of any partial-volume correction is a source of variability, with substantially different results possible from scanners of different resolutions, as shown by Grady (19).
Explaining the magnitude and shape of an observed SUV distribution would require a rigorous quantitative examination of individual statistical distributions of every variable component in Equation 1. However, the scope here is limited to commenting on the possible dominant causes of variability. The relative importance of protocol versus physiologic factors might be judged from the following:
In studying lung cancer, Minn et al. (20) found excellent FDG PET reproducibility in the same patient, obtaining CVs for SUVs and glucose-corrected SUV-leans (i.e., calculated from lean body mass not total body weight) of only 0.1 and 0.06, respectively. Similarly, for a variety of malignancies, Weber et al. (21) found the same patient reproducibility with a 0.09 CV for SUVs.
Many investigations of the cerebral glucose metabolic rate (11,12) typically show CVs as low as 0.19 (Table 3), which includes both patient and PET effects.
Table 4 from the work of Avril et al. (22), showing possible SUV definitions, illustrates variations from this source. These are responsible for, at most, a CV associated with methods of about the 0.20–0.22 shown in the last row of Table 4.
Various SUV Definitions of Avril et al. with Their Receiver-Operating-Characteristic (ROC) Areas for Breast Cancer Diagnosis
The average CV of 0.55 in Table 1 is much larger than the CVs of the foregoing. This suggests that individual physiologic factors are more important than PET factors.
With data showing the left side of Equation 1 to be lognormal, the product of the first 2 (dominating the variability) explanatory factors on the right must now be lognormal. If variations in individual subfactors in these are lognormal, then a mathematic consequence is that the entire combination is lognormal. It is tempting to theorize perhaps a variability dominance from the vascular surface area per gram S: in a specific tissue (as a factor in k1) and in all body tissues (as a factor in kp). This is because it is well established (23,24) that morphologic aspects of vasculature have lognormal distributions. Also corroborating the ideas are in vitro data from an ovarian carcinoma cell line (25): FDG uptake was proportional to cell density, whose distribution is lognormal (6) and relates to S.
The range noted for the CVs or σs of FDG among malignancies can also be discussed within the context of Equation 1. From Bartlett's test result, ranging was wider than would be expected if all cancers had the same intrinsic CV. However, the test showed that this range, 0.11–0.32 for σ in Table 1, was not excessively large for 25 investigations. Some insight might come from isoleucine uptake (26) in normal rat brain as a well-defined tissue type: CVs remaining essentially constant in spite of PS values being made, by concentration changes, to span a factor of 200. Perhaps in line with this, diverse cancer categories, with no doubt widely varying PS values, might be expected to have at least not a drastically wide range of CVs.
Potential Applications in Diagnoses
Considering our results and the above discussion, specific applications in the diagnostic process arise.
Quality Assurance.
Checks are desirable for a new tracer investigation or for an institution initiating PET studies in a particular category. With sufficient patient and lesion numbers (perhaps 20 or more), multiple comparisons with row values in Tables 1 and 2 can provide stringent tests for the newer work. This testing is whether it is within expectations relating to means and CVs measured in prior investigations.
Outliers and P Values.
Advantages of transforming data to a Gaussian variable to facilitate statistical testing have been discussed by Bland and Altman (16). One reason for doing this is to permit the use of parametric tests that require Gaussian behavior. Such tests have more statistical power (i.e., use fewer patients or reduce chances of error in conclusions [or both]). This contrasts with the required use of less powerful nonparametric tests on skewed SUVs. Some instances in which investigators have tested skewed SUV data, rather than Gaussian log10SUVs, using parametric methods are now known to be incorrect; false conclusions could have resulted possibly from erroneous P values. It is easy to appreciate that forcing an assumed Gaussian shape on a skewed distribution such as Figure 1A can lead to a very poor representation of the tails, which influence statistical decision making.
Receiver-Operating-Characteristic Curves.
Receiver-operating-characteristic (ROC) curves now can be constructed more accurately over wider ranges with fewer patient data. After transforming SUVs to log10SUVs, a 2-parameter fit to a Gaussian distribution is possible. This provides a basis for extrapolations into distribution tails beyond data. If need be, it is even possible with limited data to use historical information on σ. This would permit approximating a distribution when only its measured mean is available. Once the best distribution curves for available numbers of patients for both malignant and benign or normal categories are gotten, the construction of an ROC is straightforward (Appendix).
Figure 3 illustrates generic ROCs on double probability paper (Appendix). Noteworthy is its primary dependency on only a ratio of S̅U̅V̅s. Secondarily, there is also a σ dependence that is not shown because this ROC uses its generic 0.23 value for both malignant and benign or normal distributions.
Generic ROCs for use in approximately describing any cancer category. Parameter shown identifying line is log10(S̅U̅V̅mal/S̅U̅V̅ben), where subscripts indicate malignant and benign, respectively. Better straight-line descriptions are possible, provided there is sufficient number of patients. These would improve on 0.23 used for SDs of both malignant and normal log10SUVs in calculations here.
A 2-tailed diagnostic test using 2 SUV cutoffs to discriminate among 3 conditions is a unique example. In a lung cancer investigation (27), adequate benign (with lower SUVs) and malignant (with moderately higher SUVs) cases existed for construction of a reliable ROC. However, 2 cases of blastomycosis were encountered with very high SUVs (10.8 and 16). The lognormal distribution of the latter (based on a geometric mean of 13 and a representative 0.23 σ for logarithms) was then approximated. When used with that of the malignant cases, it then becomes feasible to construct a preliminary additional ROC—that is, an ROC for discriminating malignant cases from blastomycosis—using an additional high SUV cutoff.
Test Figure of Merit.
The diagnostic capabilities of 2 tests having lognormal test values x, such as SUVs, may be compared using a simple figure of merit (FOM). Suggested is (Appendix, geometric mean usage)
 Eq. 2
where
Eq. 2
where
 Eq. 3
may be used to characterize test effectiveness. The larger the FOM, the larger the ROC area, which, using the probability function (Appendix), is Φ(FOM). Figure 4 shows this function. When lacking better information, the σt may be approximated with an average over all tissue types, (0.232 + 0.232)1/2 = 0.33, based on Tables 1 and 2.
Eq. 3
may be used to characterize test effectiveness. The larger the FOM, the larger the ROC area, which, using the probability function (Appendix), is Φ(FOM). Figure 4 shows this function. When lacking better information, the σt may be approximated with an average over all tissue types, (0.232 + 0.232)1/2 = 0.33, based on Tables 1 and 2.
ROC area for comparing tumor diagnostic protocols. Parameters identifying these lines are total SDs—that is, square root of sum of squares of σs belonging to benign and malignant log10SUV distributions. For central line, its (0.232 + 0.232)1/2 = 0.33 is typical σt of cancer categories of investigations here.
An example of this FOM is using Equations 2 and A7 for the calculated set of results appearing in Table 4. The intention is to find the most appropriate SUV definition for breast cancer diagnosis. Table 4 shows that the simply obtained analytic results agree well with areas from special ROC curve-fitting software. Moreover, formulas can help to understand why a particular method is superior to another.
Interinstitutional Comparisons.
Keyes (14) has critically questioned the use of published SUVs outside an investigator's institution. As discussed above, when there were 3 or more investigations of the same cancer category (which often included various histopathologic types), the results were significantly different. It would be especially inappropriate for an institution to blindly use a (benign versus malignant) cutoff SUV recommended by another institution. This is because of a need to thoroughly compare protocols and makeups of patient populations and to agree with outcomes' cost–utility assignments explicitly or implicitly made in optimizing cutoff.
Until standardized approaches are adopted, the options in Table 4 and other protocol variations known to affect SUVs should be recognized (1,12–14). Sometimes a choice of a best SUV definition is recommended for a given tissue, as in the work of Avril et al. (22). For the present, the practice of an author attaching a designator to the SUV acronym is commendable, though rare. As an example, SUVavl(55) would indicate average pixel values, lean body mass, and 55 min after injection.
It is also important to heed proper characterizations of patient populations. From the discussion of Equation 1, patient factors, rather than PET factors, are implied as the more important contributors to SUV variability. Noted in the discussion of Table 3 was identification of patient factors (11,12) as helpful in reducing CVs of cerebral glucose metabolic rates. One step in this direction in oncology is the often-seen listing of SUVs with the histopathology, along with other descriptive disclosures.
SUV Ratios, CVs, and Geometric Means.
These quantities arise out of relationships from usage of logarithms (Appendix) and are intrinsically more appropriate to use than SUV differences, SDs, and arithmetic means. In particular, in light of Figure 2, the use of severity, as SUV ÷ a population's S̅U̅V̅, departing from unity is a universal measure that is independent of cancer type.
CONCLUSION
This work should bring out an awareness of an inherent logarithmic and multiplicative nature of tracer uptake. Distribution data supporting this are convincing. It is encouraging to note this commonality of a Gaussian distribution of log10SUVs of all cancer and other tissue categories with many other lognormally distributed quantities in biology. On the other hand, more work is needed for a quantitative understanding of a possible explanatory law of proportional effects unfolding in tracer uptake at the cellular level.
On the basis of our findings, several practical diagnostic aids are suggested. These lead to a belief that benefits in information portability among institutions could result from steps taken in at least 2 directions: standardizations of PET protocols along lines of reducing variabilities and more attention to detail regarding factors within a cancer category population that might influence individual SUVs. Narrowly defined subcategories that are based on histologic characteristics may be the ultimate groupings for defining SUV distributions.
APPENDIX
Lognormal Distribution and Associated Parameters
A value x (such as SUV) is lognormal (28) if the distribution of n values of its logarithms can be adequately described by the Gaussian distribution probability density
 Eq. A1The lognormal distribution of xs is then
Eq. A1The lognormal distribution of xs is then
 Eq. A2Here σ is the SD of the log10(x) values and x̅ is their geometric mean having relationships
Eq. A2Here σ is the SD of the log10(x) values and x̅ is their geometric mean having relationships
 Eq. A3
Eq. A3
The CV of the xs can be related to σ when variations are not too large.

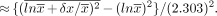 Eq. A4
Eq. A4
 Eq. A5For data of the type in Table 1, the error of this approximation is <10% in about two thirds of its applications.
Eq. A5For data of the type in Table 1, the error of this approximation is <10% in about two thirds of its applications.
For any distribution of values y (whether SUVs or log10SUVs), skew is defined as
 Eq. A6It is 0 for perfectly symmetric distributions but otherwise is a quantitative measure of asymmetry. Its SE when there are n samples is (6n/[(n − 1)(n − 2)])1/2.
Eq. A6It is 0 for perfectly symmetric distributions but otherwise is a quantitative measure of asymmetry. Its SE when there are n samples is (6n/[(n − 1)(n − 2)])1/2.
Cumulative Distribution Function and Associated Graphs
The integral of Equation A1 or Equation A2 up to the value x is the cumulative distribution function nΦ(x). The probability integral Φ appears commonly in mathematic tables and software. nΦ(x) is the number of values occurring below a cutoff x. For a malignant population, 1 − Φ(x) is the sensitivity; for a benign or normal population, Φ(x) is the specificity.
Plots of Φ against its argument can become straight lines if the Φ axis is distorted into a probability paper's axis. This ordinate (Figure 2), invisibly marked off in uniform units of numbers of SDs, has the corresponding values of 1 − Φ visibly marked at desired locations. If the abscissa's independent variable on this probability paper is Gaussian, data points will then define a straight line. The slope (in SD units per abscissa unit) is the reciprocal of the independent variable's SD. For lognormal data, a logarithmic paper's axis can be convenient, as in Figure 2.
ROCs
An ROC can be constructed from 2 cumulative distribution function plots, a malignant distribution plot and a benign or normal distribution plot. If overlapping Gaussian distributions are involved, their Φs are straight lines on probability paper. This linear behavior then carries over to the ROC. Figure 3 shows 2 probability axes used. Thus, straight-line graphic ROC fitting is an alternative to more complex fitting requiring special software.
A commonly used measure of diagnostic capabilities, especially in comparing tests, is the area under an ROC. It has been shown (29,30) that for overlapping Gaussian distributions
 Eq. A7where σt is the square root of the sum of squares of the 2 SDs. The means' difference for lognormal SUVs is log10S̅U̅V̅mal − log10S̅U̅V̅norm = log10(S̅U̅V̅mal/S̅U̅V̅norm), with geometric means used. Thus, a large means ratio and a small σt result in a large ROC area and a highly discriminating test.
Eq. A7where σt is the square root of the sum of squares of the 2 SDs. The means' difference for lognormal SUVs is log10S̅U̅V̅mal − log10S̅U̅V̅norm = log10(S̅U̅V̅mal/S̅U̅V̅norm), with geometric means used. Thus, a large means ratio and a small σt result in a large ROC area and a highly discriminating test.
Law of Proportionate Effects
A set of yis can have its distribution of values influenced by how changes among these individual values occur. In many processes, small changes are proportional to existing values (28).
 Eq. A8
Eq. A8
 Eq. A9For example, in the angiogenesis process y would be S, the total capillary vessel area per gram, which increases by some random fractional amount ri in each time interval. When Equation A9 is summed on both sides, the result on the left, ln(final y ÷ initial y) and, hence, ln(final y), is Gaussian. The reason stems from the central limit theorem for generating Gaussians from random numbers: When many of the latter are summed, the total is Gaussian. Thus, in the example here, lnS is Gaussian because many generations of random growth factors occurred.
Eq. A9For example, in the angiogenesis process y would be S, the total capillary vessel area per gram, which increases by some random fractional amount ri in each time interval. When Equation A9 is summed on both sides, the result on the left, ln(final y ÷ initial y) and, hence, ln(final y), is Gaussian. The reason stems from the central limit theorem for generating Gaussians from random numbers: When many of the latter are summed, the total is Gaussian. Thus, in the example here, lnS is Gaussian because many generations of random growth factors occurred.
Footnotes
Received Aug. 13, 1999; revision accepted Feb. 1, 2000.
For correspondence or reprints contact: Joseph A. Thie, PhD, Biomedical Imaging Center, The University of Tennessee Medical Center at Knoxville, 1924 Alcoa Hwy., Knoxville, TN 37920.










