Abstract
Dose kernel convolution (DK) methods have been proposed to speed up absorbed dose calculations in molecular radionuclide therapy. Our aim was to evaluate the impact of tissue density heterogeneities (TDH) on dosimetry when using a DK method and to propose a simple density-correction method. Methods: This study has been conducted on 3 clinical cases: case 1, non-Hodgkin lymphoma treated with 131I-tositumomab; case 2, a neuroendocrine tumor treatment simulated with 177Lu-peptides; and case 3, hepatocellular carcinoma treated with 90Y-microspheres. Absorbed dose calculations were performed using a direct Monte Carlo approach accounting for TDH (3D-RD), and a DK approach (VoxelDose, or VD). For each individual voxel, the VD absorbed dose, DVD, calculated assuming uniform density, was corrected for density, giving DVDd. The average 3D-RD absorbed dose values, D3DRD, were compared with DVD and DVDd, using the relative difference ΔVD/3DRD. At the voxel level, density-binned ΔVD/3DRD and ΔVDd/3DRD were plotted against ρ and fitted with a linear regression. Results: The DVD calculations showed a good agreement with D3DRD. ΔVD/3DRD was less than 3.5%, except for the tumor of case 1 (5.9%) and the renal cortex of case 2 (5.6%). At the voxel level, the ΔVD/3DRD range was 0%–14% for cases 1 and 2, and –3% to 7% for case 3. All 3 cases showed a linear relationship between voxel bin-averaged ΔVD/3DRD and density, ρ: case 1 (Δ = –0.56ρ + 0.62, R2 = 0.93), case 2 (Δ = –0.91ρ + 0.96, R2 = 0.99), and case 3 (Δ = –0.69ρ + 0.72, R2 = 0.91). The density correction improved the agreement of the DK method with the Monte Carlo approach (ΔVDd/3DRD < 1.1%), but with a lesser extent for the tumor of case 1 (3.1%). At the voxel level, the ΔVDd/3DRD range decreased for the 3 clinical cases (case 1, –1% to 4%; case 2, –0.5% to 1.5%, and –1.5% to 2%). No more linear regression existed for cases 2 and 3, contrary to case 1 (Δ = 0.41ρ – 0.38, R2 = 0.88) although the slope in case 1 was less pronounced. Conclusion: This study shows a small influence of TDH in the abdominal region for 3 representative clinical cases. A simple density-correction method was proposed and improved the comparison in the absorbed dose calculations when using our voxel S value implementation.
Molecular radionuclide therapy with 131I has been the standard treatment for thyroid carcinoma for more than 50 y of clinical practice, but its treatment planning remains based on a standard amount of activity defined according to the nature of the residual tissues (1). Other targeted radionuclide therapy (TRT) modalities have been developed such as peptide receptor radionuclide therapy for neuroendocrine tumors (NET), radioimmunotherapy for antibody-targeted tumors (e.g., non-Hodgkin lymphomas [NHL]), and selective internal radiation therapy for hypervascularized tumors, all with the potential for toxicity to normal tissues. At this time, only the treatment regimen of NHL with 131I-tositumomab requires patient-specific dosimetry. Indeed, whole-body dosimetry is performed using a dosimetric dose of 131I-tositumomab before the patient therapeutic administration (2). However, most of the aforementioned TRT modalities are still administered using a standard amount of radioactivity or at best by adapting the amount of radioactivity to the patient body weight or surface area (3,4).
Individual dosimetry can be implemented with a certain level of personalization using 3-dimensional (3D) quantification and standard absorbed dose coefficients (S value), which are available from official MIRD publications (5–7) and can be corrected for patient organ mass (8). Indeed, 3D quantification methods using SPECT or PET can be implemented in clinical routine (9), using full iterative reconstruction, including CT-based attenuation correction, as well as scatter effect and collimator response compensations. The software package OLINDA/EXM (10) provides the tools for organ and suborgan dosimetry, including biologic data-fitting and a comprehensive S value library. However, several limitations have already been pointed out, mainly regarding the impossibility of accounting for heterogeneous activity distribution within compartments (11) and the simplicity of the spheric tumor model and tumor inclusion (12).
A much higher level of personalization can be obtained with a fully 3D dosimetry for which each step of the dosimetry is performed at the voxel level to allow editing of descriptive statistics, dose–volume histograms (DVHs), and isodose curves.
At this level of personalization, 2 options are available: direct Monte Carlo simulation (MC) and dose kernel convolution (DK).
Direct MC methods are based on generic MC codes such as MCNP (Monte Carlo N-Particle) or EGS (Electron γ-Shower). They can take into account both radionuclide and tissue density distributions, thus presumably leading to an accurate absorbed dose distribution assessment. For these reasons, MC methods are considered as the reference. MC methods have been implemented in software tools, such as 3D-RD (13), SIMDOS (14), and OEDIPE (15).
To speed up the computation, DK approaches have also been proposed. The first was the dose point-kernel method (16), which was later extended to voxel sources (dose voxel-kernel) in MIRD pamphlet 17 (17) by the introduction of voxel S values (VSV). Absorbed dose calculation by DK, either by dose point-kernel or dose voxel-kernel, can take into account radionuclide distribution at the voxel level, but rapid implementations using fast Fourier transform or fast Hartley transform impose the use of an invariant kernel and, thus, the assumption of uniform tissue density. The DK methods are implemented in software tools such as VoxelDose (18) and RMDP (19).
Direct MC simulations involve a higher computation time than convolution approaches, particularly if one wants to achieve a low statistical noise at the voxel level, making it challenging for clinical practice. On the other hand, fast implementations of DK approaches may be not suitable for highly heterogeneous body regions such as the thorax or bone sites. It has been shown that the differences between the 2 approaches in a homogeneous medium amount to no more than small discrepancies in the average absorbed dose and at the voxel level (11,20). Consequently, the DK approaches, in cases for which the homogeneous tissue density assumption can be made, are equivalent to direct MC computations.
Previous studies have discussed the impact of tissue heterogeneities on the energy deposition of electrons, especially on the backscatter effect (21–24). Indeed, the perturbations of material interfaces were quantified in terms of backscatter dose factor as described by Buffa et al. (23) for point sources. The feasibility of using dose point-kernel scaling methods has been shown by Janicki et al. (25) and Loudos et al. (26). Furthermore, Furhang et al. (27) have included an equivalent distance method in an MC approach.
The dosimetry of TRT is often focused in the abdomen either for tumor localization (NETs, hepatic hypervascularized tumors, or NHLs) or for organs at risk (liver, kidney, or spleen). Indeed, in radioimmunotherapy, tumors can be present in the abdominal region and toxicity can occur for liver, kidneys, or spleen (28). In peptide receptor radionuclide therapy, tumors can be present in the abdomen, and the kidney is an organ at risk because of the retention of radiopeptides or radiometals (29). Also, the goal of selective internal radiation therapy is to control the tumor while preserving the nontumoral liver (30).
Consequently, our goal was to study the influence of tissue density heterogeneities (TDH) on abdominal 3D dosimetry and in extend, the hypothesis of a homogeneous tissue density. The use of simple density correction methods at the voxel and organ level, similar to the organ mass correction proposed in MIRD pamphlet 5 (8), was also investigated. To this aim, 3 representative clinical cases were studied.
MATERIALS AND METHODS
Input Data
The 3 clinical cases included the following: case 1, a NHL patient treated with unlabeled tositumomab, followed by 131I-tositumomab (Bexxar therapeutic regimen; GlaxoSmithKline); case 2, a patient who had clinically suspected NETs and for whom dosimetry for possible therapy using 177Lu-peptides was simulated; and case 3, a hepatocellular carcinoma (HCC) patient treated with 90Y-loaded microspheres.
For each case, the input data were the time-integrated activity (TIA) map derived from the SPECT images and the density map obtained from the CT scan and interpolated to the SPECT voxel size. Both dose calculations (MC and DK) were based on the β–, atomic electron, and photon components of 131I, 177Lu, and 90Y decay spectra obtained from the RADTABS program (31).
3D-RD
The MC calculation was performed with the software tool 3D-RD (32), based on the EGSnrc (EGS National Research Council Canada) code. A more complete description of 3D-RD has been previously provided (13). Briefly, 10 million events were run using 8 parallel processes on a node of a Beowulf-class cluster (EGSnrc MC software). The output values from the MC method given as energy deposition distribution from the contributing components per decaying particle were weighted for probability and TIA and then converted to absorbed dose for each voxel by dividing by the voxel mass. The absorbed dose
VoxelDose
The DK calculation, implemented using VSV, was performed with the software tool VoxelDose (18). This implementation will be referred to as VD. The VSVs were precalculated with MC code MCNPX (33) at a fine voxel size, with the tissue medium set to soft tissue as defined by the International Commission on Radiation Units and Measurements (ρ = 1.04 g⋅cm−3) (34). The dose calculation itself, as described by Dieudonné et al. (11), encompasses the resampling of the VSV at the voxel size of the TIA map and the rapid convolution via a fast Hartley transform, giving the absorbed dose
Density Correction
To account for heterogeneous density distribution, a voxel density correction was applied to correct the absorbed dose within each voxel
According to MIRD pamphlet 5 (8), an average organ density correction was also applied to the average absorbed dose of each target
Absorbed Dose Comparison
The absorbed dose maps computed with 3D-RD were used as the reference. The comparison between the 3 VSV implementations (VD, VDd, and
At the voxel level, density-binned
The DVHs were computed in the tumor of case 1 and in tumor and healthy liver for case 3.
Case 1: 131I-Tositumomab.
Case 1 concerns a NHL patient with a periaortal abdominal tumor who was imaged after the administration of 200 MBq of 131I-tositumomab as a tracer and subsequently treated with the same radiopharmaceutical. This patient’s data have previously been described and published (35). Abdominal SPECT/CT images were acquired on a Phillips Precedence SPECT/CT scanner (16-slice) at 48, 72, and 144 h after tracer administration. The SPECT images were reconstructed using the QSPECT method (30 iterations, 16 subsets per iteration) (36,37), based on the iterative ordered-subsets expectation maximization algorithm with reconstruction-based compensation for attenuation, scatter, and the collimator–detector response function. The resulting matrix was 128 × 128 × 87 (3.91 × 3.91 × 4.25 mm). The different reconstructed SPECT images were then registered over time using a HERMES workstation. The activities for the different voxels were fitted as a function of time with a hybrid trapezoid–exponential fit and integrated to obtain the voxel TIAs. The defined VOIs for this patient were the kidneys, spleen, liver, and tumor.
Case 2: 177Lu-Peptide.
Case 2 concerns a patient with clinically suspected NETs, examined at the University Hospital of Lausanne and injected with 185 MBq of 111In-pentetreotide (OctreoScan; Covidien) for diagnostic imaging. Three SPECT images of the abdominal region were acquired at 4, 24, and 48 h after injection with a 3-head γ-camera (Triad; Trionix Research Laboratory, Inc.), using a medium-energy collimator and 15% energy windows centered at 171 and 245 keV. This patient’s data have also been described and published previously (38). The SPECT images were reconstructed and registered in a manner identical to that in case 1. The resulting matrix was 128 × 128 × 128 (4.48 × 4.48 × 4.48 mm). The voxelized activity was adjusted for the difference in physical half-life between the pretherapeutic (111In, 67.3 h) and planned therapeutic (177Lu, 6.73 d) isotopes. The functional fit to the voxelized activities was a simple exponential. VOI contours were drawn for the kidneys, liver, and spleen. Furthermore, a distinction was made between the renal cortices and medullae. This patient was not treated because no tumors were evidenced in the 111In images. This case was selected for its relevance to 177Lu renal dosimetry.
Case 3: 90Y-Microspheres.
Case 3 concerns an HCC treated with 1.0 GBq of 90Y-loaded resin microspheres. The data were collected from the pretherapeutic procedure, which requires the injection of 99mTc-macroaggregated albumin (MAA) (30), that is, 99mTc injected activity and a 99mTc-MAA SPECT/CT dataset. The patient had a perfused volume of 99mTc-MAA of 1,500 cm3 and a liver tumor of 714 cm3. The 99mTc-MAA SPECT/CT dataset showed a potential 90Y gastric uptake. The SPECT/CT data were acquired on a Symbia T2 γ-camera (Siemens Healthcare) at the nuclear medicine department of Beaujon Hospital. The data processing has been described and published previously (39). The reconstruction was performed using a 3D ordered-subsets expectation maximization algorithm (6 iterations and 8 subsets) on Syngo MI workplace (MIWP; Siemens Healthcare) with attenuation, scatter, and nonuniform collimator response compensations. The reconstructed SPECT voxel size was 4.8 × 4.8 × 4.8 mm. The CT image was registered with MIWP. The TIA map was derived from the 99mTc-MAA SPECT/CT dataset, assuming similar distributions within the liver for 90Y-microspheres and 99mTc-MAA after adjustment was made for the difference in radionuclide physical half-life (64.1 vs. 6.02 h, respectively).
This study was approved by the local ethical committee, and all patients signed a written informed consent form.
RESULTS
With the MC calculation, 2–3 h were required to generate 10 million events using a single cluster node (with 8 parallel processes), for each time point and decay type (photon, β-particle, and atomic electron). On a desktop computer, the calculation time for the DK method was below 10 s for each case.
The comparison of the average absorbed dose to organs and tumors is given for each case in Tables 1–3⇓⇓. Only 2 absorbed dose differences between
Average Absorbed Dose Comparison for Case 1
Average Absorbed Dose Comparison for Case 2
Average Absorbed Dose Comparison for Case 3
Transverse slices of the 3D absorbed dose maps computed with 3D-RD and VoxelDose are given in Figure 1 for each case. At the voxel level, the
Case 1: images of NHL treated with 131I-tositumomab. Transverse slice of absorbed dose calculated with 3D-RD (A) and VoxelDose (B) without density correction (VD) is shown. Main differences between both absorbed dose maps are due to MC statistical fluctuations (A). Case 2: simulation of 177Lu-peptide. Transverse slice of absorbed dose calculated with 3D-RD (C) and VoxelDose (D) without density correction (VD) is shown. Case 3: HCC treated with 90Y-microspheres. Transverse slice of absorbed dose calculated with 3D-RD (E) and VoxelDose (F) without density correction (VD) is shown. Dashed lines represent tumor boundaries.
Case 1: NHL treated with 131I-tositumomab. Linear correlation between density-binned average absorbed dose differences ΔD and density ρ, for absorbed doses above 1 Gy and ρ ≥ 0.9 g⋅cm–3, is shown. (A) ΔD between 3D-RD and VoxelDose with homogeneous density (VD). (B) ΔD between 3D-RD and VoxelDose with density correction (VDd). Case 2: simulation of 177Lu-peptide. Linear correlation between density-binned ΔD (average absorbed dose differences) and ρ (density), for absorbed doses above 1 Gy and ρ ≥ 0.9 g⋅cm−3, is shown. (C) ΔD between 3D-RD and VD.(D) ΔD between 3D-RD and VDd. Case 3:HCC treated with 90Y-microspheres. Linear correlation between density-binned ΔD (average absorbed dose differences) and ρ (density), for absorbed doses above 1 Gy and ρ ≥ 0.96 g⋅cm−3, is shown. (E) ΔD between 3D-RD and VD. (F) ΔD between 3D-RD and VDd.
The use of density correction on VD computation globally improved the agreement with 3D-RD. At the organ and tissue levels, both
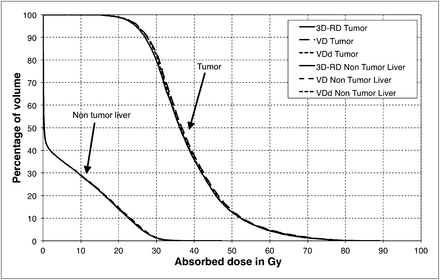
The DVHs are presented for the
Case 1: NHL treated with 131I-tositumomab. DVH in tumor calculated by 3D-RD, VoxelDose with homogeneous density distribution (VD), and with density correction (VDd).
Case 3: HCC treated with 90Y-microspheres. DVH in and tumoral and nontumoral liver calculated by 3D-RD, VoxelDose with homogeneous density distribution (VD), and with density correction (VDd).
DISCUSSION
The purpose of this study was to evaluate the accuracy of 3D abdominal dosimetry, assuming the hypothesis of homogeneous tissue density when using a DK approach. A simple density correction at the voxel level was also proposed and evaluated. Our results show a small influence of TDH in the abdominal region for the 3 representative clinical cases studied. Nevertheless, the proposed density correction method improved absorbed dose calculated with DK.
We chose to focus on the abdomen because of the small differences in tissue density and because numerous administrations of TRT are of interest due either to the presence of tumors or to the potential for normal-organ toxicity. Three representative clinical cases were considered. Case 1 was a NHL patient treated with 131I-tositumomab. Case 2 was a patient with a clinically suspected NET treated with 177Lu-peptide. Case 3 was an HCC patient treated with 90Y-microspheres.
For each case, the absorbed dose calculation was performed with 2 approaches. First, a direct MC method implemented in the software tool 3D-RD (32), taking into account voxel density, was considered as the reference. Second, we used DK, with a revision of the VSV method (17). This method was implemented in the software tool VoxelDose (or VD) (18), assuming a homogeneous density distribution (ρ = 1.04 g⋅cm−3). Both implementations (3D-RD and VD) were previously compared in a homogeneous soft-tissue medium for 90Y and 131I, with discrepancies below 1% (11). Regarding the statistical equivalence of both approaches, the MC simulations were done with 107 histories for each decay component, and the VSV kernels were calculated with 109 histories (11). Therefore, the VD calculation is statistically equivalent to an MC simulation with 109 histories per voxel. Although the statistical uncertainties between 3D-RD and VD are not equivalent, the voxel-based comparison is not affected, because the absorbed dose differences were binned (toward density) before being plotted against density.
The calculation time with MC was much longer than when using our VD method, but this should not hide the fact that VSVs require long prior calculations and an algorithm to be adapted to the voxel size of the γ-camera. Furthermore, with DK in general, and VSV in our case, it is not possible to integrate the effect of TDH on the energy deposition. Therefore, a postcalculation density correction is proposed and investigated. Its principle is to correct the absorbed dose for each voxel by scaling it with the real density values derived from CT data. This correction would not adjust the fluency perturbations of primary particles (photons or electrons) but only the local energy deposition of secondary charged particles (electrons).
The organ and tumor level comparison between 3D-RD and VD shows a limited impact of tissue heterogeneities, with relative differences on the average absorbed dose,
Slices of the 3D absorbed dose maps computed with 3D-RD and VD show similar aspects (Fig. 1). Because of the statistical nature of MC simulations (3D-RD), the corresponding absorbed dose maps are less smoothed than the ones obtained with the VD method.
At the voxel level, the comparison between 3D-RD and VD showed a
The density corrections at the voxel and organ levels improved the dose calculation with VD, with
The density correction at the voxel level improved the agreement between 3D-RD and VD at the voxel level. Indeed, the voxel absorbed dose relative difference
Our results are valid in the conditions we met—that is, the abdominal region and radionuclides with major dose contribution coming from the electron emissions (atomic and β–). The comparison was done with specific MC and DK implementations, namely 3D-RD and VoxelDose, respectively. 3D-RD was chosen as the gold standard with the advantage of being well established, with a history of clinically relevant publications.
Further studies will have to be undertaken with different conditions for any extension of these results to other treatment localizations, radionuclides. Additionally, the implementation of scaling methods that were proposed for internal dosimetry (25–27) could be investigated in other conditions—that is, with a major photon emission component or with sites in the thoracic region or bone.
CONCLUSION
There is a small but significant influence of tissue density heterogeneity on the absorbed dose calculation in the abdominal region for radionuclides with a preponderant β-emission (i.e., 131I, 177Lu, and 90Y). A simple density correction at the voxel level was proposed for DK methods, allowing improvement of the absorbed dose calculation.
DISCLOSURE
The costs of publication of this article were defrayed in part by the payment of page charges. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 USC section 1734. No potential conflict of interest relevant to this article was reported.
Footnotes
↵* Contributed equally to this work.
Published online Dec. 18, 2012
- © 2013 by the Society of Nuclear Medicine and Molecular Imaging, Inc.
REFERENCES
- Received for publication March 19, 2012.
- Accepted for publication August 29, 2012.