Abstract
To improve radioimmunotherapy with anti-CD66 antibody, a physiologically based pharmacokinetic (PBPK) model was developed that was capable of describing the biodistribution and extrapolating between different doses of anti-CD66 antibody. Methods: The biodistribution of the 111In-labeled anti-CD66 antibody of 8 patients with acute leukemia was measured. The data were fitted to 2 PBPK models. Model A incorporated effective values for antibody binding, and model B explicitly described mono- and bivalent binding. The best model was selected using the corrected Akaike information criterion. The predictive power of the model was validated comparing simulations and 90Y-anti-CD66 serum measurements. The amount of antibody (range, 0.1–4 mg) leading to the most favorable therapeutic distribution was determined using simulations. Results: Model B was better supported by the data. The fits of the selected model were good (adjusted R2 > 0.91), and the estimated parameters were in a physiologically reasonable range. The median deviation of the predicted and measured 90Y-anti-CD66 serum concentration values and the residence times were 24% (range, 17%−31%) and 9% (range, 1%−64%), respectively. The validated model predicted considerably different biodistributions for dosimetry and therapeutic settings. The smallest (0.1 mg) simulated amount of antibody resulted in the most favorable therapeutic biodistribution. Conclusion: The developed model is capable of adequately describing the anti-CD66 antibody biodistribution and accurately predicting the time–activity serum curve of 90Y-anti-CD66 antibody and the therapeutic serum residence time. Simulations indicate that an improvement of radioimmunotherapy with anti-CD66 antibody is achievable by reducing the amount of administered antibody; for example, the residence time of the red marrow could be increased by a factor of 1.9 ± 0.3 using 0.27 mg of anti-CD66 antibody.
In radioimmunotherapy, antibodies are used to selectively deliver radioactivity to cancer or bystander cells (1–3). Radioimmunotherapy has been most successful in the treatment of more accessible malignancies (4) such as leukemia. For radioimmunotherapy of leukemia, antibodies directed to the antigens CD33, CD45, and CD66 have been extensively investigated (3). Several studies with radiolabeled anti-CD66 antibody have been conducted so far (5–13).
The efficacy of radioimmunotherapy depends on a variety of factors (2). The application of pharmacokinetic models has helped to elucidate the most important influences for favorable antibody biodistribution (14). Physiologically based pharmacokinetic (PBPK) models (15,16) have the great advantage that the parameters used represent a physiologically meaningful quantity, and the experimental conditions can be related to the effect (on a specific parameter) in the patient (17–19). For radioimmunotherapy with anti-CD45 antibody (18), the application of a PBPK model demonstrated that the amount of unlabeled antibody, administered as a preload, is a main determinant of favorable biodistribution. For radioimmunotherapy with anti-CD66 antibody, the influence of the amount of antibody on the biodistribution has not yet been quantified. The use of an optimal amount of antibody for 111In and 90Y labeling might considerably improve the biodistribution (18) and therefore enhance the efficacy and reduce the side effects such as nephrotoxicity (10,20).
It has been reported that the biodistributions of 111In- and 90Y-labeled antibody are similar when both labeled compounds were administered simultaneously (21). However, the assumption that the biodistribution during dosimetry is equivalent to the therapeutic biodistribution may not be justified, if the number of accessible antigens is in the same range as the number of antibodies or the amounts of antibody used for dosimetry and therapy differ considerably (18).
In this study, 2 PBPK models are presented to investigate the influence of the amount of administered anti-CD66 antibody on the biodistribution. The model that is most supported by the data was selected using the corrected Akaike information criterion (AICc) (22). The predictive power of the best model, that is, the capability of the model to predict the therapeutic biodistribution based on pretherapeutic measurements, was validated comparing the actually measured concentration during therapy and the simulated concentration of 90Y-labeled antibody in serum. To quantify the amount of antibody resulting in the most favorable biodistribution, therapeutic biodistribution was simulated for varying amounts (0.1–4 mg) of antibody.
MATERIALS AND METHODS
Patients
Patient characteristics (n = 8) are presented in Table 1. All patients were treated in 2 study protocols approved by the Ethics Committee of Ulm University, and all patients gave their written informed consent. Patients with acute leukemia were eligible for radioimmunotherapy if they were deemed to be at high risk of relapse (>30%) after standard myeloablative chemoradiotherapy (protocol 1) or reduced-intensity conditioning (protocol 2). Further inclusion criteria included being in first complete remission for patients with high-risk cytogenetics or in second or higher remission for all other patients. Patients had to have a human leukocyte antigen compatible matched related or unrelated donor and be free of concomitant medical conditions that would exclude them from chemoradiotherapy.
Patient and Treatment Characteristics
Pharmacokinetic Study
The measurements were performed between June 2008 and February 2009, as described elsewhere (23). In brief, the patients received an intravenous injection of 0.44 ± 0.09 mg of anti-CD66-antibody labeled with 132 ± 25 MBq of 111In. Blood samples were obtained at 5 and 30 min; 1, 2, and 4 h; and 1, 2, 3, and 6 d after injection. Planar whole-body scintigraphy (anterior and posterior views) with a double-head γ-camera (ECAM; Siemens) was performed at 2 and 4 h and 1, 2, 3, and 6 d after injection to evaluate the distribution and elimination of the radiotracer (Fig. 1).
Anterior (mirrored) and posterior γ-camera images (48 h) of patient 6.
Blood samples drawn during therapy at 5 and 30 min; 1, 2, and 4 h; and 1 and 2 d after the injection of 1.17 ± 0.30 mg of anti-CD66-antibody labeled with 3.2 ± 0.8 GBq of 90Y were used to validate the model. The 111In and 90Y serum activity was measured using a γ-counter (Auto-γ-5003; Canberra Packard). The percentage of administered activity was calculated using the conjugate-view method with triple-energy window scatter correction as implemented in the ULMDOS program (24).
Antibody Labeling
The anti-CD66 antibody (BW250/183) used in this study is described by Ringhoffer et al. (9). The labeling with 111In or 90Y was conducted in 2 steps. First, the bifunctional chelator [2-(p-SCN-Bz-)-6-methyl-diethylenetriaminepentaacetic acid [DTPA]] was attached to the antibody, and second the radioisotope was bound to the chelator. Briefly, 10 mg of antibody and 18 mg of mx-DTPA were incubated at pH 8.5 for 2 h at room temperature and 15 h at 4°C. Then excess mx-DTPA was removed using gel filtration/size-exclusion chromatography. Subsequently, fluorescence-activated cell sorting (FACS) analysis was used to test an aliquot of the antibody–chelator complex for immunoreactivity. The immunoreactivity was greater than 90%. Radiolabeling was conducted, incubating the antibody–chelator complex with yttrium chloride or indium chloride at a pH of 5.0–5.5 for 5 min (90Y) and for 30 min (111In) at room temperature. To evaluate the radiochemical purity, an aliquot of the labeled antibody was subjected to size-exclusion chromatography–high-performance liquid chromatography. The antibody solution was sterilized using Millipore filtration.
PBPK Model Development
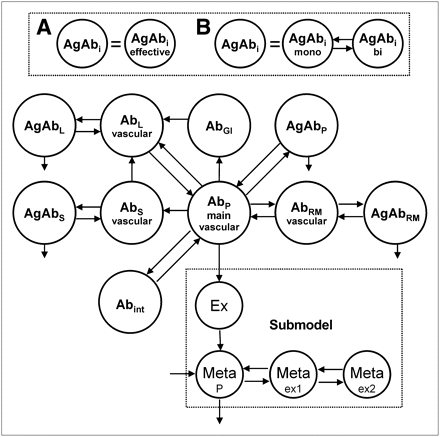
Two PBPK models (Fig. 2) were developed to describe and predict the biodistribution of anti-CD66 antibody using the modeling software SAAM2 (University of Washington) (25). The PBPK models include 4 major antigen (Agi)–expressing sites (red marrow, spleen, liver, and blood), association and dissociation of antibody to antigens (kon, koff, KD), degradation and excretion of bound (λdb) and unbound antibody (λdu), blood volumes (Vi), and blood flows (Fi) to the specific organs (18).
PBPK model of unlabeled antibody. Complete model consists of 2 circulating systems (1 for labeled and 1 for unlabeled antibody), which are connected due to competition for the same antigens in organs and physical decay. Antibody (Ab) is injected into veins (main vascular compartment). From there, antibody is distributed according to blood flow to organs. Models A and B differ in implementation of antibody–antigen binding. For model A, association and dissociation of antibody is implemented in 1 step; model B allows monovalent and bivalent binding. Bound antibody degrades with same rate in each organ.
For the spleen, liver, and red marrow, specific antibody uptake was modeled directly from the blood compartment, because blood flows through discontinuous capillaries in organs of the reticuloendothelial system (26,27). Bordessoule et al. (28) reported CD66 liver antigen sites; however, Bosslet et al. (29) found no binding of BW250/183 antibody in liver tissue. The exchange of antibody across continuous capillary walls (as found in skin or muscle) is slow, compared with the fast transport to antigen sites in the red marrow, spleen, or liver (27). The transport of antibody to the interstitial spaces was modeled according to Eger et al. (26). For reasons of parsimony, only blood flows and volumes (30) of organs, for which considerable CD66 expression and high accessibility was expected, were explicitly incorporated. Other vascular spaces (e.g., veins, arteries, heart) are merged into 1 general blood compartment.
Modeling the distribution and the competitive binding of labeled and unlabeled antibody requires 2 circulation systems (18) (composed of the described features in Fig. 2), which are connected by a stationary number of antigens Ag0,i of all organs and radioactive decay λphy.
Furthermore, it is assumed that bound antibody degrades with the same rate λdb wherever it is specifically bound. The degradation of nonbound antibody (rate λdu), clearance (rate λcl), and distribution of antibody fragments (fractions of 111In-DTPA and 111In low molecular weight of degraded labeled antibody) were modeled according to the empiric submodel of Eger et al. (26) (Fig. 2). We have also assumed that the distributions of 111In-DTPA and 90Y-DTPA are equal.
The measured radiochemical purity was implemented by simultaneous bolus injections into the respective compartments: the main free antibody compartment and the Ex compartment (Fig. 2) (26).
Models A and B differ in the modeling of the binding of antibodies to antigens. Model A uses effective values for the monovalent association rate kon,eff, dissociation rate koff,eff,i, and dissociation constant KD,eff,i; model B explicitly includes monovalent (kon,mono and koff,mono) and bivalent binding (kon,bi and koff,bi) (31–33).
Data Fitting and Parameter Estimation
The total blood volumes Vtotal; the number of antigens Ag0,i of the red marrow, liver, spleen, and blood; the blood flows to the red marrow Frm; and the red marrow scaling factor β (24) were estimated individually (for each patient). To account for the radioactivity of large vessels overlapping the lumbar spine, the blood volume of the L2–L4 vessel Vregion of interest was incorporated using the mean value of this blood volume as determined by Meredith et al. (34). Degradation of bound antibody was globally fitted; that is, a common parameter was assumed for all patients together. The calculation time increases exponentially with the number of patients; thus, to estimate common values, the patients (n = 8) were divided in 2 groups for global fitting (Table 1). Blood flows to the red marrow Frm were fitted individually (with a Bayesian term) as they are among the most powerful parameters (35) of PBPK models, and it has been reported that leukemia alters red marrow blood supply (36). The following 2 paragraphs describe how parameter estimation for model A and model B differs.
Model A
The effective dissociation constant KD,eff,i strongly depends on the ratio of antibodies to antigens (32) and therefore on the organ i. However, kon,eff should be the same for all patients and organs as described in Ong and Mattes (32). Thus, the association rate kon,eff was estimated globally, whereas the dissociation constant KD,eff,i was determined for each organ individually.
Model B
kon,mono and kon,bi—the intrinsic association rates (specific for the binding of this antibody to the CD66 antigen)—were globally estimated. Experimentally determined dissociation constants of anti-CD66 antibody binding values from the literature are apparent constants and not intrinsic values. As mentioned, for the determination of global parameters the data of 4 patients (P1–P4 and P5–P8) were used simultaneously.
The parameter value for the dissociation rate (koff, 0.3/min) was taken from the literature (37). Furthermore, it was assumed that the dissociation rate had the same value for mono- and bivalent binding (31).
The modeling software SAAM2 (University of Washington) (25) was used for data fitting with the implemented Rosenbrock least-squares algorithm. A relative data-weighting scheme with a fractional SD of 0.1 was assigned to all (sample size of 111In time–activity data for 4 patients, n = 128) data, and the convergence criterion was set to 10−5 (25).
The corrected AICc was used to select the model that was most supported by the data (38–40). To calculate the AICc values and the Akaike weights, the number of data points, number of estimated parameters, and sums of squares are needed, as described in the supplemental materials (available online only at http://jnm.snmjournals.org).
Model Validation
First, the quality of the fits was assessed by the adjusted R2. Second, the estimated parameters (and corresponding SD) were checked against the values reported in the literature. Third, the predictive power of the model was evaluated by comparing the measured serum concentration of 90Y-anti-CD66 with the predicted concentrations for therapy (15) and by comparing the true and the predicted residence times τserum. The mean deviations for all patients were calculated as follows: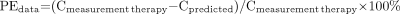
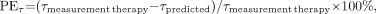where PEdata and PEτ are the performance error of the predicted serum concentration Cpredicted and the serum residence time (τpredicted). To assess the general difference between the serum kinetics of dosimetry and therapy, the serum concentrations and the residence times were compared:
The residence times of the measured data τmeasurement therapy and τmeasurement dosimetry were determined by fitting the data to a function with 2 exponential terms and subsequent (analytic) integration to infinity.
Computer Simulations
To investigate if radioimmunotherapy with anti-CD66 antibody can be improved by the administration of different amounts of labeled antibody, various therapeutic scenarios were simulated on the basis of the developed model. The residence times of all organs were determined for 0.1–4 mg of antibody used to label 90Y. For all simulations, the actual amounts of antibody administered for 111In measurements were used.
RESULTS
Using the AICc for model selection, we found that model B (bivalency explicitly implemented) was more strongly supported by the data (100% model B; 0% model A). The resulting time–activity curves fit well (Figs. 3A and 3B; Table 2). The estimated parameters and the corresponding SD of model B are presented in Table 2; the results of model A and the calculations pertaining to the model selection are presented in the supplement (Table B). The blood volumes (41), blood flows (30), degradation rates (26), monovalent association rate (37), and number of antigens (42) were all in a physiologically reasonable range. Interestingly, the ratio of the bivalent and monovalent association rate was approximately 80 times higher than suggested by Kaufman and Jain (33).
Data, fits, and simulations of patient 6. (A) Fitted curves for organs of interest and total body. (B) Fit of blood curve for 0–144 h together with predicted curve and corresponding blood measurements. (C) Simulated residence times for range of 0.1–4 mg of antibody administered for therapy. Corresponding graphs for all patients are presented in supplemental materials. RM = red marrow.
Adjusted R2 and Fitted Parameters of Empirically Most-Supported Model (Model B)
The predictive power of model B was evaluated, comparing the measured and the simulated (predicted) serum concentration (5 min to 48 h) during therapy (Fig. 3B). For 8 patients, the median deviation of prediction and 90Y plasma measurement PEdata is 24% (range, 17%−31%), and the median deviation of the predicted and measured residence time PEτ was 9% (range, 1%−64%). The median values for Δdata and Δτ, here used as a measure for the general difference of 111In and 90Y data, are 45% (18%−53%) and 53% (30%−62%), respectively.
Simulations (based on the validated model and the estimated parameters) of the therapy biodistribution for various amounts of antibody (0.1–4 mg) yielded a monotonically decreasing residence time for the red marrow and monotonically increasing residence times for the liver, spleen, and blood (Fig. 3C) with the amount of antibody. The therapeutic residence times of all organs for the actual and the optimal amount are presented in Table 3. Using 0.27 mg of antibody, which corresponds to 1 nuclide per antibody for an average activity of 3.2 GBq, would have increased the residence time of the red marrow by a factor of 1.9 ± 0.3 (Table 3).
Residence Times τi of Therapy
DISCUSSION
To improve radioimmunotherapy with anti-CD66 antibodies, 2 predictive PBPK models for radioimmunotherapy with 90Y-labeled anti-CD66 antibody have been developed. Model A incorporates effective values for the association and dissociation process, and model B allows monovalent and bivalent binding. These models were fitted to the radioimmunotherapy data of 8 patients. The AICc showed that model B is most supported by the data (100%).
The estimated parameters, besides kon,bi, compare favorably with literature values. The step from mono- to bivalent binding seems to be 80 times faster than calculated using the numbers of Kaufman et al. (33). Further investigations are needed to verify whether all the assumptions (33) (e.g., koff, mono equals koff, bi, transformation from bulk to surface association rates or the mobility of antibody and antigen) are applicable for this antibody–antigen interaction. The numbers of CD66 antigens, compared with the numbers of CD45 antigens, appear to be low (18); however, our results confirm studies concluding that, in general (if not stimulated), CD66 is expressed at relatively low levels on resting granulocytes (42).
The predictive power of the model was investigated on the basis of the parameters determined by fitting the models to the measured biodistribution data. The predictive accuracy of model B is good for the serum concentrations and excellent (except patient 3) for the residence times. We do not have an adequate explanation of why the predictive accuracy of patient 3 (PEτ, 64%) differs from the other 7 patients (PEτ median, 5%; range, 1%−28%). In general, the validation—being the evaluation of the quality of the fits, plausibility of the estimated parameters, and determination of the predictive power—is positive.
The measurement of the serum concentration of antibody for the validation of the predictive power is sufficient for radioimmunotherapy with anti-CD66 antibody, because the kinetics of the plasma time–activity curve are primarily dominated by the uptake of the antibody by the organs, especially the red marrow. Thus, the serum activity mirrors the number of antigens in the marrow, in which more CD66-expressing cells are located than in liver, spleen, or blood. The studies of Bosslet et al. (29) have been confirmed in that binding in the liver was low. In contrast to a study (including patients with inflammatory disease) conducted by Steinsträsser et al. (43), negligible binding of antibody to circulating blood granulocytes was observed. Measurements of whole blood and serum (for patient 3, whole-blood data not shown) yielded low binding (difference of blood and serum was between 1% and 3%) of antibody to granulocytes. This was confirmed for all patients by the estimated parameters (the number of antigens in the blood was undetectably low; Table 2) and by FACS analysis (average mean fluorescence intensity was 315 ± 79). It is not surprising that the number of antigens in the blood was estimated to be 0 for nearly all patients, because the total granulocyte pool in red marrow is approximately 100 times higher (mean Agrm, 7 nmol) than in blood. The apparent contradiction between our results and the results of Steinsträsser et al. (43) may be explained by the investigation of different patient populations, because Steinsträsser et al. studied the biodistribution in patients with inflammation for whom CD66 is upregulated (42).
Although 90Y- and 111In-labeled antibodies have similar biodistribution when applied simultaneously (21), the assumption that biodistribution is equal for dosimetry and therapy is not justified when considering our data. The model predictions are considerably closer to the measured 90Y-anti-CD66 serum data than the measured 111In-anti-CD66 serum data. These measurements and the estimated model parameters show that saturation of antigen sites plays an important role in the clinical use of anti-CD66 antibody, which in response requires adequate dosing.
On the basis of the validated model, the optimal amounts of antibody were investigated by simulating the therapeutic biodistribution. For a range of 0.1–4 mg of anti-CD66 antibody, we calculated the residence times for red marrow, spleen, liver, and serum (Fig. 3C). As a result, we found that labeling 0.1 mg of antibody with 90Y activity would have led to the most favorable biodistribution for all investigated antibody amounts. This is plausible because we found that 99% of anti-CD66 antibody is bound in the red marrow. Having such an antigen distribution, the concept of preloading (18) is not helpful to improve the biodistribution; however, a reduction of the antibody dose allows more radiolabeled antibodies to bind in the marrow. The results suggest that reducing the amount of antibody to the mass of 0.27 mg (which corresponds to 1 antibody per nuclide for the average therapeutic dose of 3.2 GBq in this study) would considerably improve the biodistribution (Fig. 3C). Faster blood clearance will potentially avoid unnecessary toxicity to the liver, spleen, and kidneys.
CONCLUSION
The application of PBPK models enabled us to identify the strong influence of the amount of anti-CD66 antibody on the biodistribution. We found that the biodistribution of dosimetry and therapy are different because of the remaining antibody from the imaging dose and application of different amounts of antibody. Most important, the selectivity of radioimmunotherapy with anti-CD66 antibody can be increased using smaller masses of antibody; for example, simulations show that for 0.27 mg of anti-CD66 antibody the residence time of the red marrow could have been increased by a factor of 1.9 ± 0.3. This probably leads to a more effective and efficient therapy. The radiation toxicity to the kidneys might be considerably reduced.
Acknowledgments
We thank Simone Gross, Peter Birkmaier, and Cornelia Dinger for their expert technical assistance and valuable suggestions. We also gratefully acknowledge a grant (GL 236/7) by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and a grant (DJCLS H 04/05) by the Deutsche Josè Carreras Leukämie-Stiftung e.V.
Footnotes
-
COPYRIGHT © 2010 by the Society of Nuclear Medicine, Inc.
References
- Received for publication June 22, 2009.
- Accepted for publication October 30, 2009.
