Combination of Converging Collimators for High-Sensitivity Brain SPECT

Collimator Combinations and Data Acquisition Trajectories

The following collimator combinations and data acquisition trajectories for triple-camera brain SPECT were studied: HCB + HCB + fanbeam, CO; HCB + fanbeam + fanbeam, CO; HCB + full-cone-beam (FCB) + fanbeam, CO; triple-HCB, CH trajectory; triple-fanbeam, CO; and triple-PB, CO.

These combinations were compared for photon detection efficiency and reconstructed image quality. Parallel-hole collimators were studied as a reference. We assumed that the HCB + PB combination was less efficient than the HCB + fanbeam combination and therefore do not consider it here. A CO implies that each of the 3 SPECT cameras, equally separated by 120°, rotates for 360°. CO sampling was 1° during simulation and experimental phantom studies and 2° during a patient brain scan. A CH trajectory implies a 300° circle followed by a 60° helix. Thus, acquisition time for the CO is 5 times longer than that for the helix, which keeps the phantom longer in the FOV and increases the photon detection efficiency. We studied whether a short-term helical trajectory with HCB collimation proposed here was sufficient for improved axial sampling. The total number of views and time per view during all data acquisitions were constant.

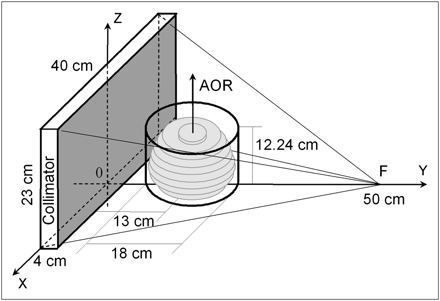
Disk Brain Phantom Monte Carlo Simulation: Collimator Parameters and Geometric Efficiency

Collimator efficiency, defined as a ratio between the number of photons detected by the γ-camera and the number emitted by the source, was calculated using Monte Carlo simulation. A disk phantom (9 disks with different radii, each 1.28 cm thick) superficially resembling the Hoffman 3-dimensional (3D) brain phantom (model BR/3D/P; Data Spectrum Corp.) in shape and size was used in the simulations. The disk radii were 6.8, 8.1, 8.4, 8.3, 7.9, 7.4, 6.7, 5.7, and 2.9 cm, listed in a caudal-to-cranial order. The phantom was centered on the axis of rotation (AOR), located 13 cm from the collimator surface. This distance is also called the radius of rotation (ROR) of the camera. The phantom disks were perpendicular to the AOR and symmetric transverse to it. The activity in the disks was assumed uniform. Similar to the physical Hoffman brain phantom, the simulated disks were located inside a cylinder (diameter, 18 cm; height, 12.24 cm). The disk brain phantom and the HCB collimator are illustrated in Figure 1. The collimator focal point was located at 50 cm from the collimator surface (shaded area, Fig. 1), defined here as the surface that is closer to the AOR. The HCB focal point was shifted axially by 11.5 cm toward the base of the phantom as measured from the center of the collimator. The focal lengths of the converging collimators were equal. All collimator FOVs were 40 × 23 cm, corresponding to the camera FOV. The collimators were 4 cm thick. Converging collimators were simulated with square holes (size, 0.145 cm) and 0.022-cm septal thickness. The hole-size parameter of the simulated parallel-hole collimator was adjusted to 0.132 cm so that the spatial resolutions of all collimators calculated on the AOR were similar. Collimator spatial resolution was modeled to include both geometric and detector intrinsic (full width at half maximum [FWHM], 0.35 cm) resolutions.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 1. 

3D sketch of HCB collimator and disk brain phantom used in Monte Carlo simulation. Phantom and collimator dimensions are shown. Phantom is centered on AOR, 13 cm from collimator surface (shaded).

Collimator geometric efficiencies vary depending on the location of the source emitting 140-keV photons. This means that photons from a certain region of the brain may have a higher or lower probability of being detected than photons from other regions. The issue is further complicated by photon attenuation and scatter inside the brain. To understand how different parts of the brain are affected by the collimator geometry, photon detection efficiencies were studied for each of the 9 phantom disks. Photon attenuation and scatter in the disks and the cylinder were modeled using the attenuation coefficient for water (μ = 0.15 cm⁻¹). The energies of the scattered photons were computed from the scattering angle, which was simulated using the Klein–Nishina formula for differential cross-section with respect to the solid angle of scattering. Photons that passed through the collimator were detected if they had energies between 126 and 140 keV. Statistical uncertainty in collimator efficiency values was less than 2%. Photon septal penetration and photopeak detection efficiency were not simulated, because they are mostly independent of the collimator types studied here.

Hoffman Brain Phantom SPECT Simulation

Along with the Monte Carlo simulation of a simplified uniform disk brain phantom to compute collimator efficiency for different disks in the phantom, we used the bitmaps of the Hoffman 3D brain phantom for projection and reconstruction in our SPECT simulation. The phantom models 19 different transaxial brain slices. To evaluate lesion visibility with the collimator configurations studied here, we placed (modeled) 3 hot and 3 cold spheres (1.1-cm diameter) in the bottom, middle, and top parts of the brain, as shown in Figure 2 bitmaps. Uptake ratios were 30% higher for the hot spheres and 70% lower for the cold spheres than they were for gray matter. The gray matter-white matter-ventricle uptake ratio in the Hoffman brain phantom used here is 4:1:0.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 2. 

Hoffman 3D brain phantom slices (bitmaps) corresponding to slice numbers 1, 6, and 11 (of 19) in caudal-to-cranial order. Three hot spheres (30% hotter than gray matter) were inserted into cerebellum (slice 1), basal ganglia (slice 6), and right parietal lobe (slice 11) of brain phantom. Three cold spheres (70% colder than gray matter) were inserted into right temporal lobe (slice 1), thalamus (slice 6), and left frontal lobe (slice 11). Arrows in figure point to lesions.

Projection data were simulated on a 256 × 128 grid using a ray-driven forward-projection algorithm. The simulated Hoffman brain phantom was reconstructed iteratively, using an ordered-subsets expectation maximization (OSEM) algorithm (19) with 24 subsets and 5 iterations for converging collimator data. The OSEM convergence rate was slightly lower for parallel-hole data and required 7 iterations to achieve bias values similar to fanbeam. Collimator resolution and sensitivity were not modeled in the ray-driven forward-projection and OSEM reconstruction algorithms. The detector intrinsic resolution of 0.35 cm in FWHM, modeled as gaussian, was used only for noisy projection data. Attenuation was modeled using a uniform map based on the phantom dimensions. The attenuation coefficient used was μ = 0.15 cm⁻¹. Scatter and septal penetration effects were not modeled in simulations. Noise-free data were used to calculate reconstruction bias with respect to the Hoffman brain phantom bitmaps. Bias was calculated for each brain slice usingEq. 1where N is the number of all pixels in a brain slice, and and are ith pixel activities in noise-free reconstructed and bitmap images. Slice-by-slice bias calculation demonstrates whether there are parts of the phantom that are more distorted than others. For instance, an HCB CO scan is expected to result in larger distortions in the cranial portions of the brain because of insufficient axial sampling, which will in turn be revealed quantitatively by larger bias values for cranial brain slices. The detector intrinsic resolution was not considered during bias calculation to avoid possible nonsampling artifacts (e.g., blur) affecting bias values.

Noisy projection data were obtained by generating an ensemble of 32 Poisson noise realizations based on noise-free bitmap projection data with a mean value of 2.7 × 10⁷ counts per fanbeam-collimated camera. The numbers of counts for other simulated collimators were scaled according to their efficiencies. The level of noise in reconstructed images for a single noise realization was evaluated slice by slice usingEq. 2for all of the pixels (N) in a brain slice. This value was then averaged over M = 32 noise realizations. Quantitatively speaking, the purpose of combining converging collimators in this study is to improve brain SPECT by decreasing both δ and σ without altering spatial resolution.

Noise reduction should positively affect the brain lesion visualization, which can be quantitatively evaluated using signal-to-noise ratios (SNRs) for the hot and cold spheres (signals) inside the simulated Hoffman brain phantom:Eq. 3

Here, 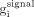and are normalized activities in the signal and the background area around it, and is the normalized background noise calculated using Equation 2 for N background pixels.

Experimental Imaging of Brain Phantom

Experimental data were acquired using a triple-camera SPECT system (Triad XLT; Trionix Research Laboratories). Collimator specifications are shown in Table 1. The fanbeam collimator used in this study had slightly better resolution because of a smaller hole size. The resulting loss of sensitivity was partially compensated for by a shorter fanbeam focal length. The focal point of the HCB collimator is unintentionally shifted 6 mm beyond the axial extent of the 40 × 23 cm FOV of the camera, which is considered during image reconstruction. The Hoffman 3D brain phantom described earlier was used in the experimental study. Each of the 19 Hoffman brain phantom slices was approximately 6.4 mm thick and consisted of 5 polycarbonate sublayers. The brain slices were placed in a polymethyl methacrylate cylinder (height, 17.5 cm; diameter, 20.8 cm). The phantom was filled with 1.4 L of water solution containing ^99mTc radiotracer (1.9 × 10⁵ Bq/cm³). There was no radioactivity in the cylinder outside the brain. Similar to simulation studies, 3 cold lesions were placed inside the physical phantom. The spheroid-shaped (grapelike) lesions had a volume of 3 mL and were filled with water with no activity. They were inserted into the cerebellum, thalamus, and frontal lobe of the brain phantom.

The 3 SPECT detectors were equally spaced by 120° and acquired data simultaneously. The detector ROR was 13 cm. There is currently only 1 HCB collimator available in our laboratory, so to produce projections for triple-HCB or HCB + HCB + fanbeam configurations, multiple single-camera scans were obtained and combined. CO data were acquired using continuous gantry rotation for 360°, with 1° sampling. HCB CH data were acquired in 2 steps: 300° revolution of the cameras around the motionless phantom, followed by additional 60° revolution with continuous phantom translation in the axial direction. During the helical portion of the scan, the phantom traveled 14.2 cm with approximately constant speed and completely exited the camera FOV by the end of the scan. This procedure was repeated twice to emulate the triple-HCB data, using the single available HCB collimator. The initial angles of the detector equipped with the HCB collimator were 0°, 120°, and 240° for the 3 separate scans. The axial positions of the phantom for each of the scans were identical.

To resemble clinical patient brain scans at Duke, we acquired about 3 million counts per camera equipped with the fanbeam collimator. Throughout the experiment, scan times were adjusted for ^99mTc decay and were equal for all collimator configurations. For instance, if the HCB + HCB + fanbeam scan started immediately after a 15-min triple-fanbeam scan, the adjusted scan time was then 15.43 min.

All data acquisitions used a 20% energy window centered at the 140-keV photon emittance peak. The data were acquired on a 256 × 128 projection grid. Iterative OSEM reconstruction was used with 6 subsets and 5 iterations. The number of subsets for the experimental studies, compared with the simulation studies, was reduced because of increased noise in the experimental data. As a result, we reduced the noise in the reconstructed images and avoided postfiltering. Photon attenuation was modeled with the “effective” attenuation coefficient μ = 0.12 cm⁻¹ (20), using a uniform map based on the brain phantom dimensions. Collimator point-spread response and scatter were not modeled in the reconstruction algorithm. Reconstructed image quality was evaluated on the basis of the level of noise, visibility of the lesions, and presence of artifacts in the images.

Patient Imaging

An interictal brain scan of an adult male patient was performed using the triple-camera SPECT system described earlier. Data acquisition for our research study followed the clinical scan and started 80 min after the intravenous administration of 10⁹ Bq (27.5 mCi) of ^99mTc-hexamethylpropyleneamine oxime. Our research scan protocol allowed for two 15-min scans with 3 γ-cameras equipped with 1 HCB and 2 fanbeam collimators (collimator specifications are presented in Table 1). During each scan, the cameras rotated continuously for 360°, with 2° sampling. The data from the second scan were reordered and combined with the data from the first scan to reproduce 2 collimator configurations of interest: HCB + HCB + fanbeam and triple-fanbeam. Both configurations contained data from a 15-min 360° scan. Thus, we acquired roughly half of the counts typically acquired during a 25-min clinical brain scan. Unavailability of more HCB collimators and a short time frame prevented us from performing a triple-HCB CH scan for comparison. HCB + HCB + fanbeam and triple-fanbeam data were compared for reconstructed image quality and the level of noise in the images.

The camera ROR was 13.5 cm. The photon detection energy window used during data acquisition was 20% (126–154 keV). The acquisition matrix size was 128 × 64. Images were reconstructed iteratively with 6 subsets and 5 iterations. Attenuation was modeled with the coefficient μ = 0.12 cm⁻¹, using a uniform map based on the dimensions of the head. Scatter was not modeled during image reconstruction.

The Institutional Review Board approved the study, and informed consent was obtained from the patients before the scan.

Collimator Efficiencies

Collimator efficiencies, calculated using Monte Carlo simulation of the disk brain phantom, are shown in Table 2. Simulations were performed with and without photon scatter modeling. Similar ratios between efficiencies with and without scatter (Table 2) indicate that scatter is mostly independent of the collimator types and acquisition trajectories studied here. Because scatter does not affect our comparative collimator and acquisition studies, it is excluded from further consideration. Contrary to scatter, photon attenuation depends on the collimator geometry. For the axially converging HCB geometry, photons emitted from the top (cephalic) portions of the cylindric brain phantom are attenuated less than the bottom (caudal) photons because of a shorter attenuation path. This is confirmed by a slice-by-slice triple-camera efficiency plot shown in Figure 3A for different collimator combinations and acquisition trajectories. For combinations involving HCB collimators, the photon detection efficiency is increased for the top 2 disks of the simulated disk brain phantom. On the basis of the plot, the HCB + HCB + fanbeam combination with CO acquisition and the triple-HCB collimation with a CH acquisition trajectory offer the highest efficiencies for every part of the disk brain phantom. The combination that includes the FCB collimator reduces the efficiency at the base of the phantom because of truncation and will not be discussed further in this article. The HCB + fanbeam + fanbeam combination is less efficient than the HCB + HCB + fanbeam combination and will also be omitted from further consideration. Triple-fanbeam and triple-PB collimations will be considered as conventional references.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 3. 

Presented for different collimator combinations and acquisition trajectories are slice-by-slice photon detection efficiencies calculated using Monte Carlo simulation (A), reconstruction bias plot for the Hoffman 3D brain phantom simulated using ray-driven method (B), and levels of noise in reconstructed images of simulated Hoffman brain phantom (C). Acquisition trajectories included a CO (not specified in legend) and CH trajectory (specified in legend). Disks and slices are numbered in caudal-to-cranial order.

Reconstructed Image Quality: Bias, Noise, and SNR

Hoffman 3D brain phantom SPECT was simulated for a triple-camera system using ray-driven forward-projection and iterative OSEM reconstruction algorithms. Noise-free reconstructions were compared with Hoffman brain phantom bitmaps to estimate reconstruction bias. Large bias values may indicate that axial sampling artifacts are present in the reconstructed images. The bias is shown in Figure 3B for all 19 slices of the phantom. Triple-HCB CO acquisition was simulated to demonstrate the extent of artifacts due to insufficient axial sampling in terms of bias values that gradually increase toward the top of the brain. The plot demonstrates that both adding a helical component to the triple-HCB acquisition trajectory and combining 2 HCB collimators with fanbeam markedly improve axial sampling of the phantom. The bias values of the HCB + HCB + fanbeam combination are comparable to triple-fanbeam bias, confirming quantitatively that reconstructed images do not display any axial artifacts. Triple-HCB CH bias values are slightly larger, especially toward the top of the brain. This is primarily due to the limited helical component of the scan. Increasing the number of helical views reduces the bias but decreases the photon detection efficiency. Nevertheless, visual analysis of the reconstructed images in our study suggests that the artifacts are hardly noticeable and should be tolerable for practical (clinical) purposes.

Along with noise-free reconstructions, we generated an ensemble of 32 noisy projection data samples for simulation studies. The noise level in the reconstructed images was evaluated slice by slice using Equation 2. The averaged results are shown in Figure 3C for all 19 slices of the simulated phantom. As expected, both the HCB + HCB + fanbeam combination and the triple-HCB CH acquisition offer reduced noise in the reconstructed images due to increased photon detection efficiency, particularly at the top of the brain. Slight efficiency advantage of the HCB + HCB + fanbeam combination at the bottom of the brain is expected and is also visible in the plot (Fig. 3C).

Reconstructed images of the simulated Hoffman brain phantom are shown in Figure 4 for all 4 acquisition types. Brain slices containing lesions are displayed. Qualitative analysis of the brain images shows reduced noise due to increased sensitivity at the same spatial resolution and confirms the advantages of the HCB + HCB + fanbeam combination and triple-HCB CH acquisition over triple-fanbeam and triple-PB CO scans. No artifacts were detected.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 4. 

Simulated Hoffman brain phantom scan results for 4 acquisition types: HCB + HCB + fanbeam CO (A), triple-HCB CH trajectory (B), triple-fanbeam (C), and triple-PB COs (D). Reconstructed images of brain phantom slices containing hot and cold lesions are shown.

Quantitatively, performances of the studied configurations were evaluated using SNRs of the lesions. Table 3 shows the SNR values for 6 lesions in the brain phantom, averaged over an ensemble of 32 noise realizations. Higher magnitudes of the SNR for the HCB + HCB + fanbeam combination and triple-HCB CH acquisition is evidence of noise reduction and better lesion visualization because of increased sensitivity. The uncertainties in the average SNR values (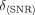) in Table 3 were calculated as follows:Eq. 4whereEq. 5is the SD of the SNR distribution for N = 32 noise realizations, assuming gaussian distribution of the SNR values. The errors can be reduced using a larger number of noise realizations.

Experimental Brain Phantom Imaging

The physical Hoffman brain phantom was scanned using the triple-camera SPECT system and 4 acquisition types described earlier. Acquisition times for each type, corrected for ^99mTc decay, were the same. The number of photons detected during each acquisition scenario is shown in Table 4. There was no truncation throughout the scan.

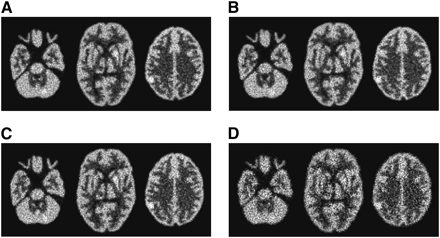
Reconstructed images of the Hoffman brain phantom are shown in Figure 5 for all 4 acquisition types. Brain slices containing cold lesions in the cerebellum, thalamus, and frontal lobe are displayed. The noise is reduced with the HCB + HCB + fanbeam collimator combination and triple-HCB CH acquisition types, compared with triple-fanbeam and triple-PB CO scans. No apparent axial sampling artifacts were observed.

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 5. 

Experimental Hoffman brain phantom scan results for 4 acquisition types: HCB + HCB + fanbeam CO (A), triple-HCB CH trajectory (B), triple-fanbeam (C), and triple-PB COs (D). Transaxial views of reconstructed brain phantom slices containing 3 cold lesions are shown, along with centrally located sagittal and coronal slices of phantom. Each slice is summed with 2 adjacent slices, to reduce noise.

Patient Imaging Data

Two 15-min interictal brain scans were obtained for a patient using the triple-camera SPECT system described earlier. We acquired 4.36 × 10⁶ photons with the HCB + HCB + fanbeam collimator combination and 2.99 × 10⁶ photons with a triple-fanbeam CO scan, which is half of the data acquired during a longer clinical interictal scan of the same patient. Scan times were equal in both cases. Reconstructed patient brain images are shown in Figures 6A and 6B. The images demonstrate improved quality with the HCB + HCB + fanbeam combination due to increased efficiency and reduced noise. To further reduce noise, images can be postfiltered using the Hann filter, with a cutoff frequency of 1.4 cycles/cm (Figs. 6C and 6D).

• Download figure
• Open in new tab
• Download powerpoint

FIGURE 6. 

Reconstructed patient brain images: centrally located transaxial, sagittal, and coronal slices are shown for HCB + HCB + fanbeam collimator combination (A) and triple-fanbeam CO acquisitions (B). Three-slice summing is used to reduce noise in A and B. Postfiltered images are shown for HCB + HCB + fanbeam (C) and triple-fanbeam (D) acquisition types.