Abstract
A dose limit–based criterion was proposed to authorize hospital discharge of thyroid carcinoma patients treated with 131I. Evaluation of accumulated doses to determine the effective half-life, the expected accumulated dose at 1 m, and the hospitalization time was performed to ensure that the dose limit was satisfied for each patient. Situations involving different dose limits and occupancy factors were analyzed. This study dealt only with external exposure; the problem of internal contamination was not considered. Methods: Fourteen patients treated postoperatively with 131I were studied. The range of activity was 1,110–8,175 MBq. Electronic dosimeters and thermoluminescent dosimeter chips were placed on the left pectoral muscle. Dose was measured for a mean of approximately 2.5 d. The accumulated doses were plotted as a function of time and then fitted using an exponential model to obtain the parameters of total accumulated dose and effective half-life. The doses to the public and relatives at 1 m were calculated with point source approximation and several occupancy factors. Results: The fit function parameters of accumulated doses in the first 36 h predicted the behavior of the total accumulated dose within a 5% error in the parameters. Estimated values of the accumulated dose 1 m from the patient were generally <5 mSv, even for an occupancy factor of 100%. For more restrictive dose constraints, hospitalization times were calculated according to different occupancy factors, as suggested in the European Commission guide. From the fit of the measured data, values of effective half-life for each patient were obtained. Conclusion: To apply the dose limit–based criterion, one must calculate the patient-specific parameters, as can be done using the accumulated dose. Knowledge of patient-specific parameters ensures that the patient will not expose any individual to levels greater than the dose limit. The calculated hospitalization times were less than those recommended, especially for countries with more restrictive dose limits. The type of measurements performed in this study reveals more realistic doses for the treatment of thyroid carcinoma with 131I.
Differentiated thyroid carcinoma occurs more frequently than any other endocrine tumor, with an annual incidence of 1.2–2.6 per 100,000 males and 2.0–3.8 per 100,000 females. Prognosis depends on age, sex, tumor stage, histologic type, and initial treatment. Radioactive iodine, 131I, has been used for more than 50 y to treat certain benign and malignant thyroid diseases. However, because of the risk of external radiation exposure to family members and the public, several criteria and regulations have been established to regulate hospital discharge of patients receiving radioactive treatment (1–7).
Almost every country has its own rules; however, they are not always alike. In Argentina, the Nuclear Regulatory Authority subscribes to the activity limit criteria. If patients receive a dose > 1 GBq (30 mCi), or if the emitting radiation dose rate at 1 m is >50 μSv/h, they need to be hospitalized in special rooms for 2 or 3 d. For the public, the established dose limit is 1 mSv/y, as has been recommended by the International Commission on Radiological Protection (ICRP) (5,6).
The Nuclear Regulatory Commission (NRC) of the United States currently recommends a modified dose limit criterion (1). The NRC “authorizes the release from its control of any individual who has been administered radiopharmaceuticals or permanent implants containing radioactive materials if the ‘Total Effective Dose Equivalent’…to any other individual from exposure to the released patient is not likely to exceed 5 mSv” (1,8). With this regulation, rather than being released only if no more than 1 GBq is administered, patients can be released regardless of the amount of administered activity, as long as the total dose to an individual at 1 m is <5 mSv.
The Radiation Protection unit of the European Commission, in its last guide, proposed dose limits related to age and family bonds (7). For family and close friends, the proposed limits were 1 mSv/y for children (including unborn children), 3 mSv/y for adults ≤ 60 y old, and 15 mSv/y for adults > 60 y old. For third parties or the general public, the proposed limit was 0.3 mSv/y.
The purpose of this study was to analyze measurement of accumulated dose as a function of time, to quantify the γ-radiation dose arising from the thyroid cancer patient treated with 131I, and to establish the individual isolation period according to the patient-specific accumulated dose curve and different occupancy factors.
MATERIALS AND METHODS
Fourteen patients who received 131I after excision of thyroid carcinoma were studied. Twelve underwent total thyroidectomy, and the remaining 2 underwent hemithyroidectomy and partial resection. The administered activity ranged from 1,110 to 8,175 MBq (30–220 mCi). Each patient was informed about the procedure and gave written consent. The patient data are shown in Table 1.
Patient Data
The accumulated dose was measured with 2 types of dosimeters: an electronic device (model PDM-253; Aloka Co., Ltd., Tokyo, Japan) for 10 patients; thermoluminescent dosimeter chips (TLDs) (TLD-100 [LiF:Mg,Ti]; Harshaw Chemical Co., Cleveland, OH) for 3 patients; and both types of dosimeters for 1 patient. For every patient, the dosimeters were placed on the left pectoral muscle. The mean measurement period was 2.5 d.
The patients recorded the information on a specially designed sheet. When an electronic dosimeter was used, the patient recorded the time of each reading; when TLDs were used, the patient wrote down the detector numbers and the exact time that these detectors were removed. The patients then put the detectors in a lead container that already held 2 TLDs as a null reference dose.
Fifty TLDs (3 × 3 × 0.9 mm) were selected for this study. They were dose calibrated with a 60Co source, and their individual sensitivity factor was obtained with a radiation source of 90Sr (9).
RESULTS
Figure 1 shows the accumulated dose measured as a function of time for 7 patients. To fit these data, we adopted for the dose rate an exponential decay function that was proportional to activity. The accumulated dose measured on the left pectoral muscle as a function of time, DM(t), is the integral time of the dose rate:
Eq. 1
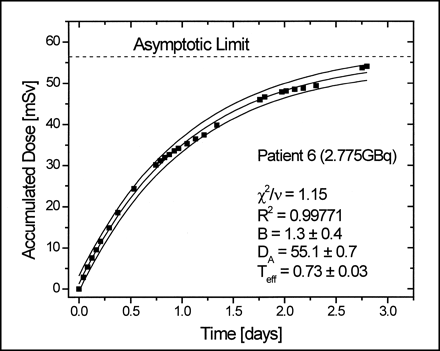
where DA is the total accumulated dose in the detector, Teff is the effective half-life, and B is an experimental parameter that accounts for the background. This last parameter allows a better fit because without it the function is restricted to passes through the origin and a bias in the residues is generated, which mainly affects Teff. Figures 2 and 3 show some examples of fit results for dose measurements with TLDs and electronic dosimeters. With the fit parameters, we can obtain DA, B, and Teff (whole body) for each patient.
Accumulated dose as function of time for each patient.
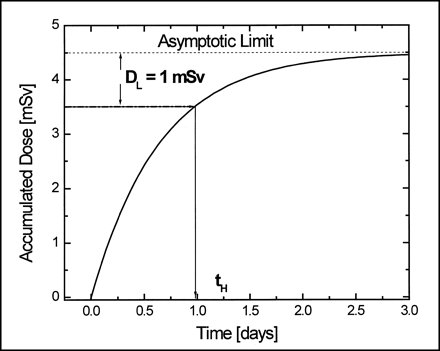
Fit results for dose measurement with TLD chip. Asymptotic limit is accumulated dose on left pectoral muscle of patient at infinity, when source activity is totally decayed. This figure shows procedure to obtain hospitalization time. Goodness of fit was tested with reduced χ2 test (χ2/v) (10).
Fit results for dose measurement with electronic dosimeter. Final accumulated dose on left pectoral muscle is asymptotic limit. Goodness of fit was tested with reduced χ2 test (χ2/v) (10).
Using point source approximation and the occupancy factor (E) concept, we could calculate the total dose to an exposed person. The approximation of the point source was conservative, because it overestimates the dose by not considering dispersion or attenuation of radiation in the patient. Besides, the point source estimates the effective dose in the whole body of the exposed person, assigning the determined value on the thorax surface. Sparks et al. (2) used the Monte Carlo method and an anthropomorphic model to calculate the dose received by an exposed person. A distributed source is assumed in the patient’s abdominal region, and the real effective dose is calculated for the whole body. In this way, the point source approximation is found to overestimate the effective dose by a factor of 2.6.
Making a conservative approximation, we consider the detector to be 20 cm from the point source. This is conservative because, in fact, the source is distributed in many organs, mainly of the abdomen, with its specific “turnover” (11). Finally, the accumulated dose in a person standing at distance r from the patient is expressed as:
Eq. 2
where DT(r,t) is the accumulated dose at distance r from the patient, at time t, counting from the time that the radioisotope is administered. E is the occupancy factor, which accounts for variations in distance from and time near the patient.
Using the dose limit–based criterion to determine the length of hospitalization, we apply the following inequality:
Eq. 3
where DT(r = 1 m, t = tH) is the accumulated dose at time tH and DT(r = 1 m, t = tH) is the total accumulated dose (both at distance of r = 1 m from the patient), tH is the hospitalization time required, and DL is the dose limit to be adopted. For the hospitalization time, we obtain the following relationship from Equations 1 and 3 using the equality:
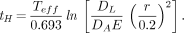Eq. 4
Figure 4 shows how this time is obtained.
Method to obtain hospitalization time.
Table 2 compares the total accumulated dose calculated using our method, for a distance of 1 m from the patient and various occupancy factors, and the method detailed in regulatory guide 8.39 of the NRC (1). This guide proposes an equation that has 2 components. The first is the dose for the first 8 h after administration with an occupancy factor of E = 0.75. The second and third are the doses from the extrathyroidal and thyroidal components, respectively, from 8 h to total decay with an occupancy factor of E = 0.25. This model uses the same parameters for all patients, modifying only the administered activity.
Accumulated Dose Obtained Using NRC Method and Our Method for Different Occupancy Factors
Table 3 summarizes the obtained Teff values, the calculated hospitalization times for different dose limits, and the occupancy factors for each patient.
Effective Half-Lives and Hospitalization Times Obtained for Different Dose Limits and Occupancy Factors
DISCUSSION
The theoretic model, which takes into consideration measurements of the accumulated dose as a function of time, correctly fit the experimental data, as Figures 2 and 3 show. For all patients, we found that the individual parameters could be determined 36 h after administration with an error of <5% toward those obtained considering total data (2.5 d). The measured accumulated dose and the dose calculated following regulatory guide 8.39 of the NRC were similar when E = 1 or E = 0.75 was adopted, as Table 2 shows. The studies that directly determined the dose in relatives or persons near the patient (12–15) found smaller values than those calculated with other conservative methods (1,7), such as ours.
Our analytic procedure allowed us to obtain Teff (Table 3). Our values were (in most cases) slightly lower than the values calculated using the proposal in regulatory guide 8.39 of the NRC (Teff = 0.67 d) (1).The NRC value is based on a biexponential model (biexponential total clearance curve), which is applied equally to all patients. It arises from considering Teff equal to F1 Teff1 + F2 Teff2, where F1 and F2 are the uptake fractions and Teff1 and Teff2 are the extrathyroidal and thyroidal effective half-lives, respectively. The NRC suggests values of F1 = 0.95 and Teff1 = 0.32 d for extrathyroidal behavior and F2 = 0.05 and Teff2 = 7.3 d for thyroidal behavior. The Teff values obtained in this study are a better option because they are obtained from an adjustment of the measured experimental data for each patient. Our model takes into consideration any distribution of iodine inside the body and the real biologic elimination from each patient.
Table 3 also shows the hospitalization times (Eq. 3) that were obtained for each patient by following the curve of accumulated doses as a function of time. The dose limits shown are 1 and 0.3 mSv, and the occupancy factors are E = 1, E = 0.75, E = 0.5, and E = 0.25. If the dose limit adopted for the public is 1 mSv, as established by the ICRP (6), then the hospitalization time for nearly every patient would be <1 d when E = 1. If E is taken to be 0.25, only 2 patients (patients 3 and 5) must be hospitalized, and for just 3 and 8.2 h, respectively.
When the dose limit adopted is DL = 0.3 mSv (proposed by the European Commission for the general public), we can consider tH to be the restriction time in social behavior. In this way, we found that the maximum restriction time was just 2.17 d for an occupancy factor of E = 1. This time is less than that suggested by the guide of the European Commission (7).
If a dose limit of DL = 3 mSv, suggested by the European Commission for adults ≤ 60 y old, is taken and the most unfavorable situation, E = 1, is considered, for only 2 patients (patients 3 and 5) do we obtain a hospitalization time of a maximum of 12 h. Table 2 shows that for a dose limit of DL = 5 mSv and an occupancy factor of E = 0.25 or E = 0.5, hospitalization is not necessary. Only 1 patient (patient 5) will need to stay in an appropriated ward, and for just 1.7 h if E = 0.75 or 5.3 h if E = 1. Table 3 shows the need to determine the hospitalization time for each patient because of the strong dependence of discharge on biologic elimination.
CONCLUSION
The dose limit–based criterion correlates directly with the basic principles of radiation protection. This criterion is associated with several advantages when compared with previous guidelines that establish patient release when the administered activity is <1 GBq or when the radiation dose rate is less than 50 μSv/h at 1 m. In this study, we used the dose limit–based criterion with different dose limit recommendations for the public (1,5–7). For a more restrictive dose limit (0.3 mSv) and 100% occupancy, the isolation time was always <2.2 d for the study group.
The variability of isolation times indicates a strong dependency of Teff on biologic half-life and shows no relationship with administered activity. Certainly, this variability reveals the need to determine these parameters for each patient. With the model proposed in this study, the dose to which individuals will be exposed at 1 m from the patient for different patterns of behavior, or occupancy factors, can be calculated. In addition, one can obtain the required isolation time for different allowed dose limits, according to the risk group or the legislation in force.
Even from a conservative standpoint, in most of the studied cases 1 d of hospitalization was sufficient. Releasing patients after 1 d of isolation with written instructions about how to keep doses to other individuals “as low as reasonably achievable” has several advantages: lower health care costs, lower doses to nursing staff, and psychologic benefits for patients and families. Emphasizing adherence to the written instructions is important, because the first hours after administration of the radiopharmaceuticals are crucial. If someone spends 1 or 2 h closer than 0.5 m to the patient during the first hours after administration, the dose limit could quickly be reached or exceeded.
Acknowledgments
The authors thank their patients for their contribution and extend special thanks to Blanca Balma and Graciela Oliva for translation assistance. This study was supported by the thermoluminescence dosimetry and environmental radioactivity program of the Centro de Excelencia en Productos y Procesos de Córdoba, CEPROCOR, Agencia Córdoba Ciencia, at the request of the Department of Endocrinology of the Hospital Privado de Córdoba.
Footnotes
Received May 7, 2001; revision accepted Sep. 25, 2001.
For correspondence or reprints contact: Carlos D. Venencia, MS, Instituto Privado de Radioterapia, Obispo Oro 423, 5000 Córdoba, Argentina.
E-mail: dvenencia{at}latin-cancer.com
